第八章--图
定义
类比前面所学的线性表和树,图就是多对多的关系。
再详细点的定义就是:图由顶点集合V(G)和边集合E(G)组成。顶点集合V(G)是一组元素的集合,这些元素称为顶点(或节点);边集合E(G)是由顶点对组成的集合,这些顶点对表示顶点之间的关系,称为边。
相关概念
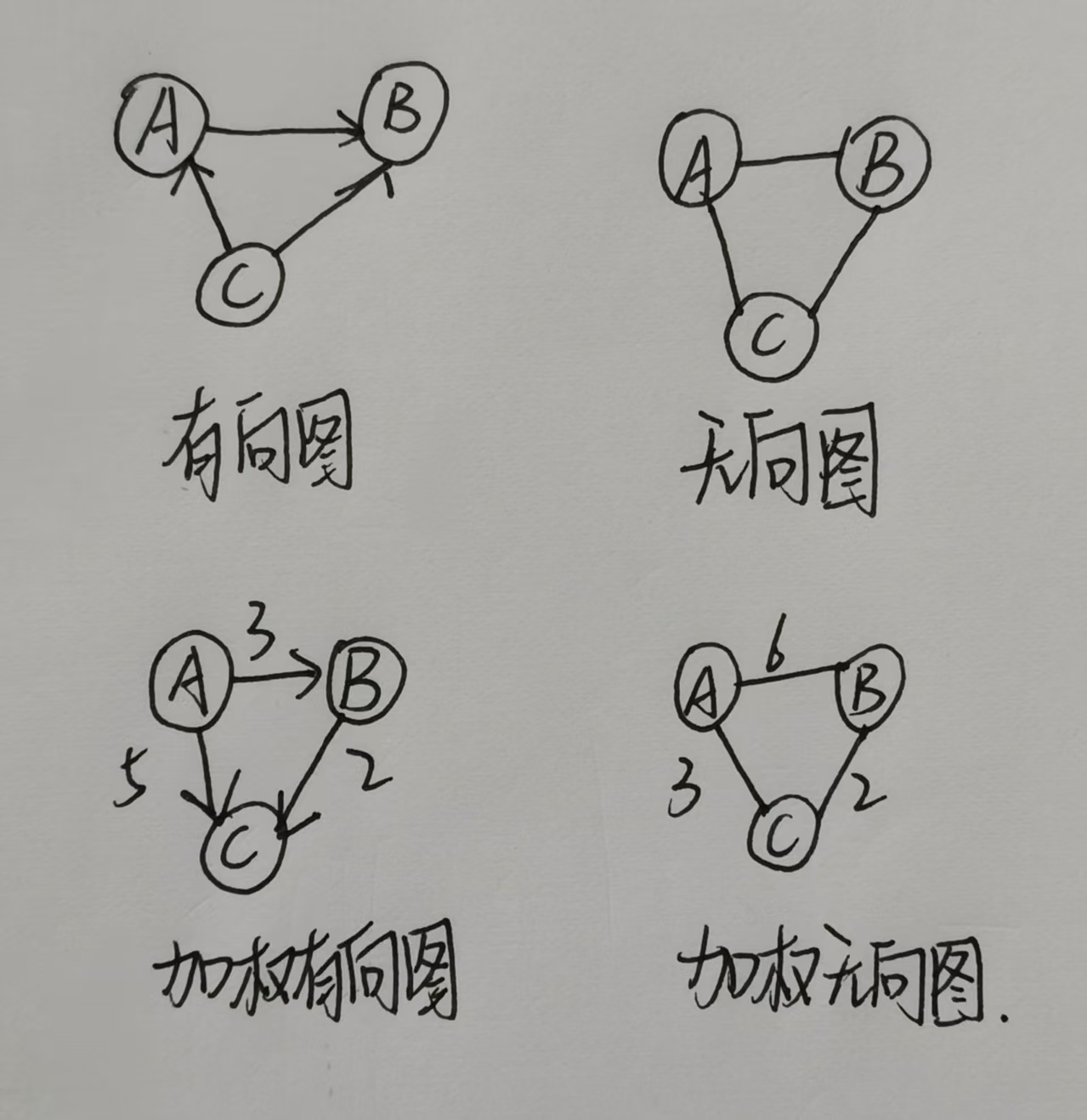
有向图:边有方向。
无向图:边无方向。
加权图:每条边都赋予一个权重(可以是表示距离、成本、时间等的数值)。
子图:设 G=(V,E) 是一个图,G'=(V',E'),如果V' V且E'
E,则称 G' 是 G 的子图。
例如:
邻接:顶点间有边相连,称顶点间有邻接关系。
出度、入度与度:有向图中一个点的出度是指由该顶点射出的有向边的条数,入度就是射入该顶点的条数du;对于无向图,度就是邻接于该点的边的总数。
简单图:一种特殊的无向图,1)图中没有自环,即不存在一条边的两个端点是同一个顶点;2)图中任意两个顶点之间最多只有一条边相连。
多重图:允许存在平行边的图,即图中可以有多个边连接同一对顶点;允许多重图存在自环。
无向完全图:无向图中任意两个不同的顶点之间都存在一条无向边,边数为。
有向完全图:边数为。
路径:在图G=(V,E)中,从顶点 到顶点
的路径是一个顶点序列
,使得对于
,
是图G中的边。如果图是有向图,那么路径中的边必须按照箭头所指的方向依次连接。路径可以分为简单路径和基本路径。简单路径是指路径中所有的边都不相同;基本路径是指路径中所有的顶点都不相同(除了起点和终点可能相同)。
回路:一条特殊的路径,它的起点和终点是同一个顶点。回路也可分为简单回路和基本回路。简单回路是指回路中所有的边都不相同;基本回路是指除了起点和终点相同外,其余顶点都不相同的回路。
图的存储方式
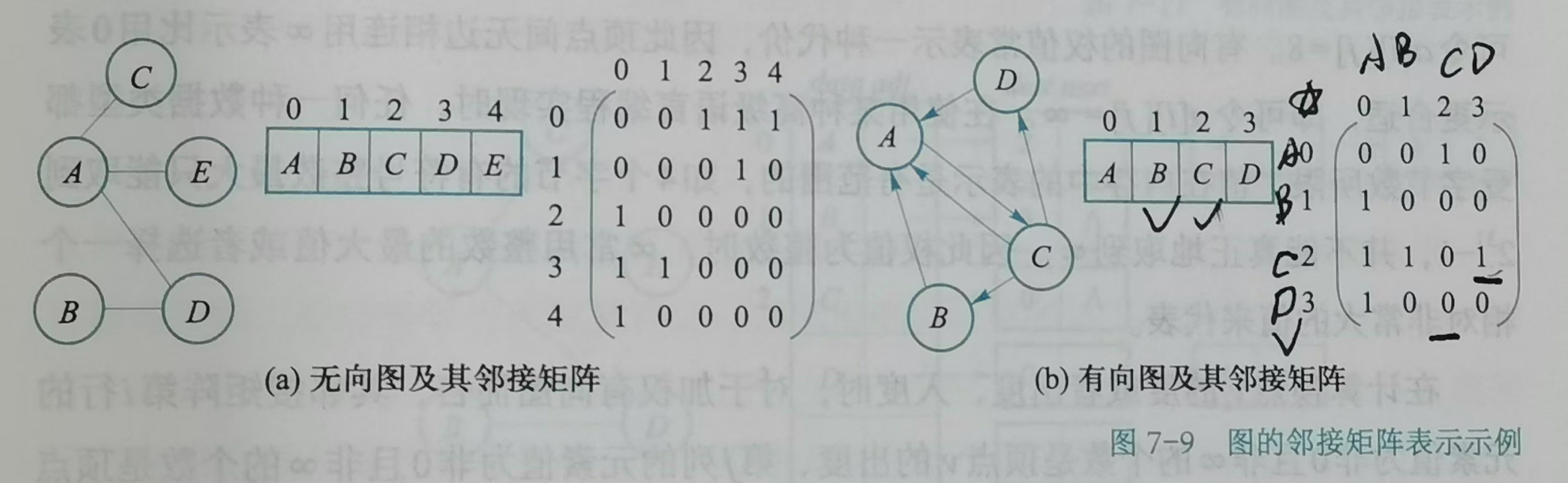
邻接矩阵表示法
直接看图:顶点用一维数组存储,矩阵上的索引代表顶点,矩阵里存储的信息代表边(1为二者有连线否则无关联)
主要是看行标。
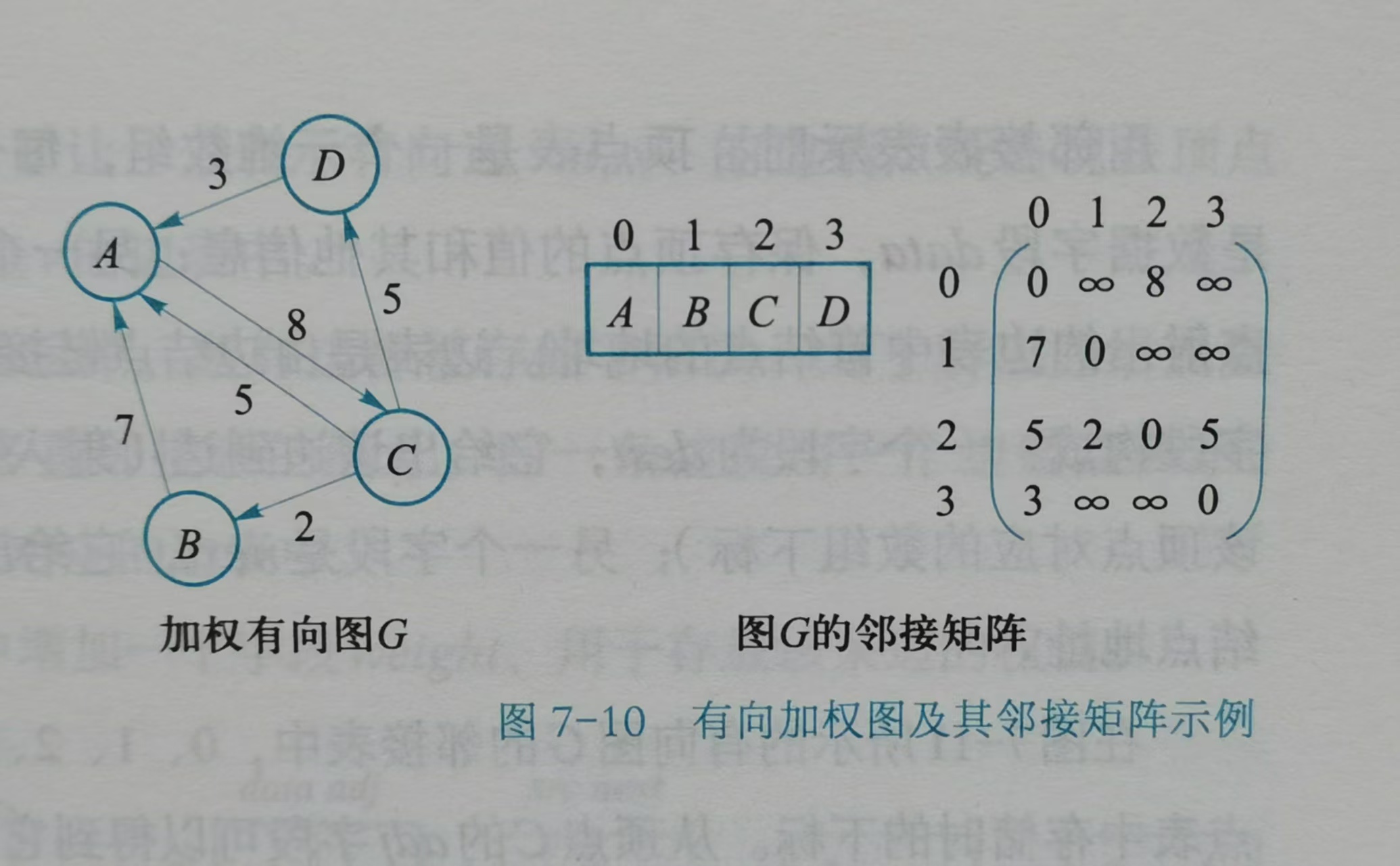
加权邻接矩阵表示法
其实与邻接矩阵表示法没什么太大区别,不过是把矩阵里存储的信息改为权值,有权值则一定有边,无穷则代表无边。
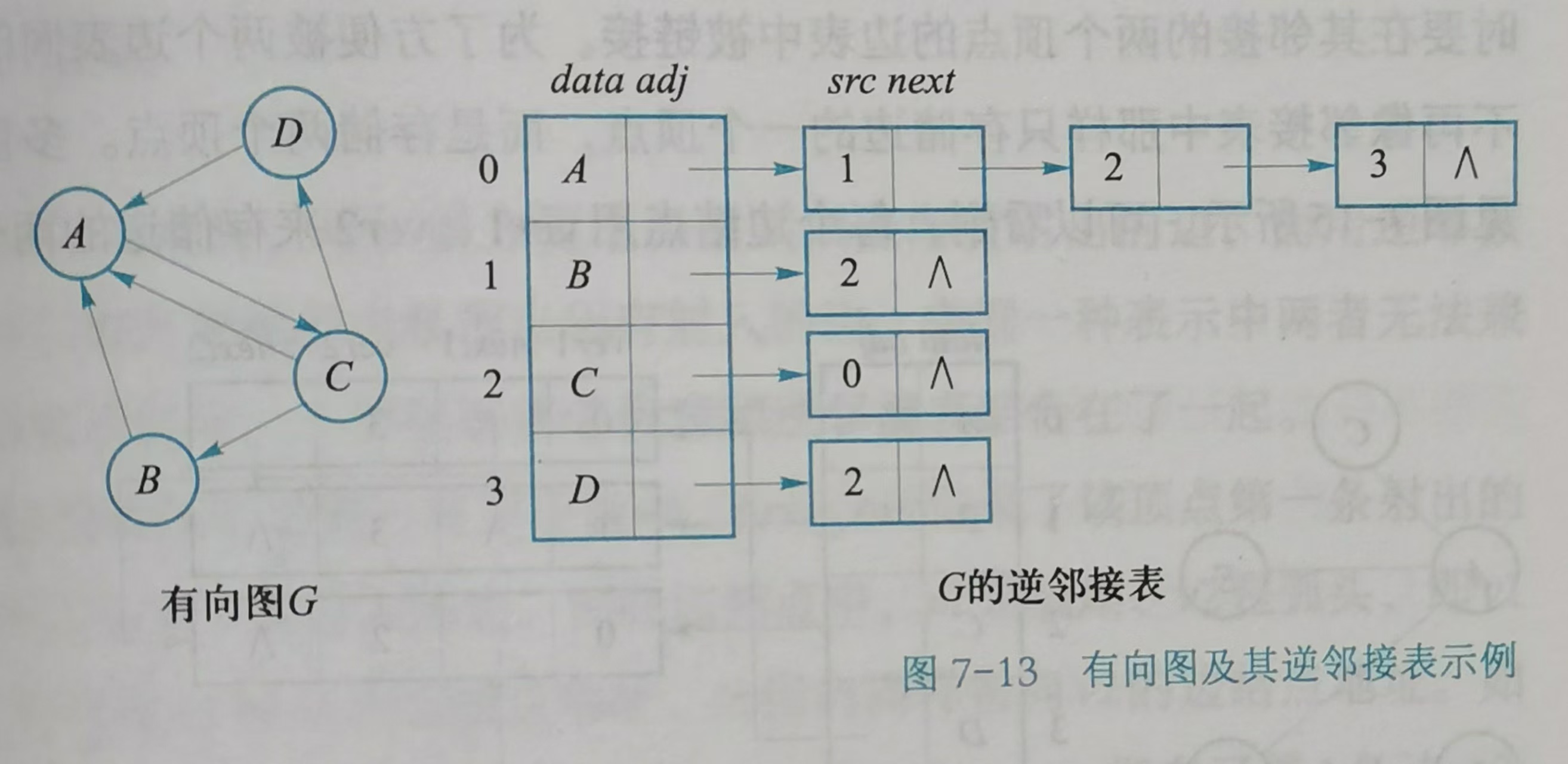
邻接表
顶点依然用一维数组存储,边由同一个顶点出发的所有边组成的一条单链表。

逆邻接表
顶点保存该顶点的射入边形成的单链表的首节点地址。
图的遍历
访问邻接点:
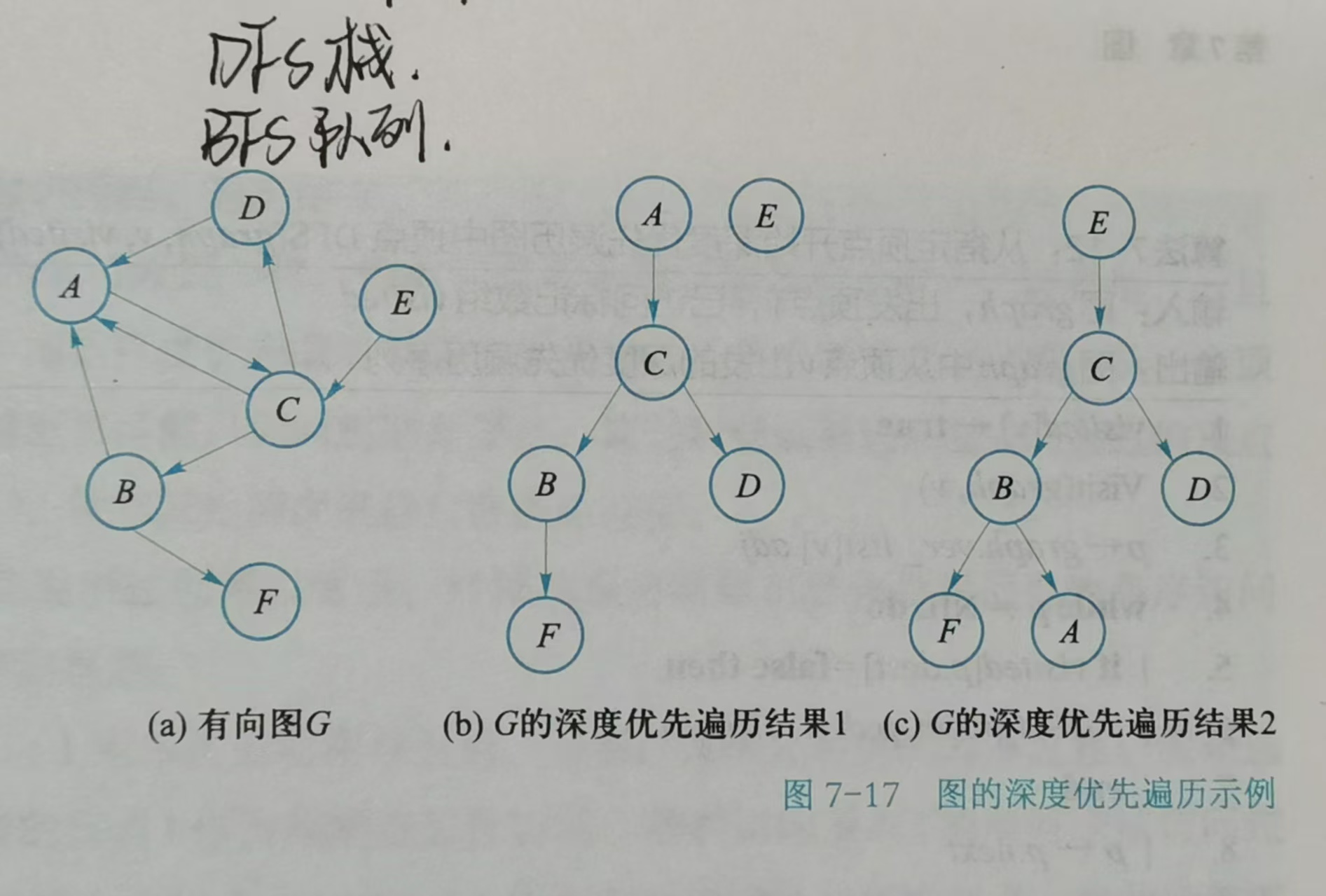
1、DFS--栈(深度优先)
2、BFS--队列(广度优先)
连通图
无向图的连通性
连通图:在无向图中,如果从顶点u到顶点v存在路径,则称顶点u和v是连通的。如果图中任意两个顶点都是连通的,那么这个无向图就被称为连通图。
连通分量:非连通图可以分解为多个连通的子图,这些极大连通子图称为连通分量。
有向图的连通性
强连通图:在有向图中,如果对于任意两个顶点u和v,既存在从u到v的路径,又存在从v到u的路径,则称该有向图是强连通图(意思就是双向的)。
强连通分量:非强连通的有向图可以划分为多个极大强连通子图,这些子图称为强连通分量
弱连通图:如果忽略有向图中边的方向后得到的无向图是连通的,则称该有向图为弱连通图(意思就是单向的)。
图的连通性判定方法
1)对于无向图,可以使用深度优先搜索(DFS)或广度优先搜索(BFS)算法从任意一个顶点出发,遍历图中的所有顶点。如果能够访问到图中的所有顶点,那么该图是连通图;否则,图是非连通图。
2)对于有向图,判定强连通性可以通过计算图的强连通分量来实现。常用的算法有 Kosaraju 算法、Tarjan 算法等。这些算法通过对图进行深度优先搜索,利用顶点的访问顺序和回溯信息来识别强连通分量。
小结
- 图的定义:图由顶点集合 V(G) 和边集合 E(G) 组成,体现多对多关系,顶点集合是元素集合,边集合由顶点对组成表示顶点关系。
- 相关概念
- 图的类型:有向图边有方向,无向图边无方向,加权图每条边有权重,子图满足顶点和边集合分别是原图的子集。
- 顶点关系:顶点间有边相连为邻接;有向图顶点有出度(射出边条数)和入度(射入边条数),无向图顶点的度是邻接边总数。
- 图的种类:简单图无自环且顶点间最多一条边;多重图允许平行边和自环;无向完全图任意两不同顶点有边相连;有向完全图任意两不同顶点有双向边。
- 路径与回路:路径是顶点序列,有向图路径边按方向连接,分简单路径(边不同)和基本路径(顶点不同,起点终点可同);回路是起点终点相同的路径,分简单回路(边不同)和基本回路(除起点终点相同外顶点不同)。
- 图的存储方式
- 邻接矩阵表示法:顶点用一维数组存储,矩阵索引代表顶点,矩阵存储边信息(1 表示有连线,0 表示无关联)。
- 加权邻接矩阵表示法:与邻接矩阵类似,矩阵存储边的权值,无穷表示无边。
- 邻接表:顶点用一维数组存储,边由同一顶点出发的边组成单链表。
- 逆邻接表:顶点保存射入边形成的单链表首节点地址。
- 图的遍历:包括深度优先搜索(DFS,借助栈)和广度优先搜索(BFS,借助队列),用于访问邻接点。
- 图的连通性
- 无向图:任意两顶点有路径则为连通图,非连通图的极大连通子图是连通分量。
- 有向图:任意两顶点有双向路径为强连通图,非强连通图的极大强连通子图是强连通分量;忽略边方向后无向图连通的是弱连通图。
- 图的连通性判定方法
- 无向图:用 DFS 或 BFS 从任一顶点遍历,能访问所有顶点则为连通图。
- 有向图:用 Kosaraju 算法、Tarjan 算法等计算强连通分量判定强连通性 。
今天的分享就到这里啦~~
