Numpy随机分布
一、随机与数据分布
通过某种生成算法产生的随机数称为伪随机数。我们能生成真正的随机数吗?是可以的。为了在我们的计算机上生成真正的随机数,我们需要从外部来源获取随机数据。这些外部来源通常是我们的按键、鼠标移动、网络数据等等。我们不需要真正的随机数,除非它与安全相关(例如加密密钥)或应用的基础是随机性(例如数字轮盘赌)。本次,我们将使用伪随机数。
NumPy 提供了random处理随机数的函数。
from numpy import randomx = random.randint(100)print(x)随机函数的rand()方法返回 0 到 1 之间的随机浮点数。
from numpy import randomx = random.rand()print(x)也可以使用上面两种方式生成数组:
(下面的所有size都是数组形状)
1、整数数组:
生成一个包含 5 个从 0 到 100 的随机整数的一维数组:
from numpy import randomx=random.randint(100, size=(5))print(x)生成一个具有 3 行的二维数组,每行包含 5 个从 0 到 100 的随机整数:
from numpy import randomx = random.randint(100, size=(3, 5))print(x)2、浮点数数组
rand()函数还允许指定数组的形状
生成包含 5 个随机浮点数的一维数组:
from numpy import randomx = random.rand(5)print(x)生成一个具有 3 行的二维数组,每行包含 5 个随机数:
from numpy import randomx = random.rand(3, 5)print(x)从数组生成随机数
该choice()函数允许根据值数组生成随机值。
该choice()函数以数组作为参数并随机返回其中一个值。
返回数组中的一个值:
from numpy import randomx = random.choice([3, 5, 7, 9])print(x)该choice()函数还允许您返回一个值数组。
添加一个size参数来指定数组的形状。
from numpy import randomx = random.choice([3, 5, 7, 9], size=(3, 5))print(x)随机分布
随机分布是一组遵循特定概率密度函数的随机数。
概率密度函数: 描述连续概率的函数。即数组中所有值的概率。
choice()我们可以使用该模块的方法 根据定义的概率生成随机数 random。
该choice()方法允许我们指定每个值的概率。
概率由 0 到 1 之间的数字设置,其中 0 表示该值永远不会出现,而 1 表示该值将始终出现。
例1:生成一个包含 100 个值的一维数组,其中每个值必须是 3、5、7 或 9。值为 3 的概率设置为 0.1,值为 5 的概率设置为 0.3,值为 7 的概率设置为 0.6,值为 9 的概率设置为 0
from numpy import randomx = random.choice([3, 5, 7, 9], p=[0.1, 0.3, 0.6, 0.0], size=(100))print(x)所有概率数的总和应该为 1。
即使运行上述示例 100 次,值 9 也永远不会出现。
可以通过在参数中指定形状来返回任意形状和大小的数组 size。
例2:与上面的例子相同,但返回一个有 3 行的二维数组,每行包含 5 个值。
from numpy import randomx = random.choice([3, 5, 7, 9], p=[0.1, 0.3, 0.6, 0.0], size=(3, 5))print(x)二、随机排列
元素的随机排列
排列是指元素的排列。例如,[3, 2, 1] 是 [1, 2, 3] 的排列,反之亦然。
NumPy Random 模块为此提供了两种方法: shuffle()和permutation()。
shuffle()函数对原始数组进行了更改
permutation()函数返回重新排列的数组(并且保持原始数组不变)
例
from numpy import random
import numpy as nparr = np.array([1, 2, 3, 4, 5])random.shuffle(arr)print(arr)from numpy import random
import numpy as nparr = np.array([1, 2, 3, 4, 5])print(random.permutation(arr))三、seaborn可视化
Seaborn 是一个使用 Matplotlib 绘制图形的库。它将用于可视化随机分布。
安装seaborn:
在终端执行以下操作:
pip install seaborn例:
import matplotlib.pyplot as plt
import seaborn as snssns.displot([0, 1, 2, 3, 4, 5], kind="kde")plt.show()Displot 代表分布图,它以数组作为输入并绘制与数组中点的分布相对应的曲线。
注意:使用sns.displot(arr, kind="kde")来可视化随机分布。
四、随机分布类型
1、正态(高斯)分布
正态分布是最重要的分布之一。它也被称为高斯分布,以德国数学家卡尔·弗里德里希·高斯命名。
它适合许多事件的概率分布,例如智商分数、心跳等。使用random.normal()函数获取正态数据分布。
它有三个参数:
loc- (平均值)钟峰所在的位置。
scale-(标准差)图形分布应该有多平坦。
size- 返回数组的形状。
例:生成大小为 2x3 的随机正态分布,其平均值为 1,标准差为 2:
from numpy import randomx = random.normal(loc=1, scale=2, size=(2, 3))print(x)可视化;
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.normal(size=1000), kind="kde")plt.show()
注意:正态分布的曲线也称为钟形曲线,因为曲线呈钟形。
2、二项分布
二项分布是一种离散分布。它描述了二元场景的结果,例如抛硬币,结果要么是正面,要么是反面。
它有三个参数:
n- 试验次数。
p- 每次试验发生的概率(例如,每次抛硬币的概率为 0.5)。
size- 返回数组的形状。
离散分布:分布是在单独的事件集上定义的,例如,抛硬币的结果是离散的,因为它只能是正面或反面,而人的身高是连续的,因为它可以是 170、170.1、170.11 等等。
二项分布与两点分布:两点分布是二项分布在n=1时的特殊情况,二项分布是两点分布在多次独立重复实验下的推广。
例:假设进行 10 次抛硬币试验,生成 10 个数据点:
from numpy import randomx = random.binomial(n=10, p=0.5, size=10)print(x)
可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.binomial(n=10, p=0.5, size=1000))plt.show() 
正态分布与二项分布区别
主要区别在于正态分布是连续的,而二项分布是离散的,但如果有足够多的数据点,它将与具有一定位置和尺度的正态分布非常相似。
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snsdata = {"normal": random.normal(loc=50, scale=5, size=1000),"binomial": random.binomial(n=100, p=0.5, size=1000)
}sns.displot(data, kind="kde")plt.show()
3、 泊松分布
泊松分布是一种离散分布。
它估计在指定时间内某个事件可能发生多少次。例如,如果某人每天吃两次,那么他吃三次的概率是多少?
它有两个参数:
lam- 发生率或已知次数,例如上述问题中的发生次数为 2。
size- 返回数组的形状。
例:为发生 2 的情况生成一个随机的 1x10 分布:
from numpy import randomx = random.poisson(lam=2, size=10)print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.poisson(lam=2, size=1000))plt.show()
正态分布vs泊松分布
正态分布是连续的,而泊松分布是离散的。但我们可以看到,对于足够大的泊松分布,它将变得类似于二项式分布,具有一定的标准差和均值。
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snsdata = {"normal": random.normal(loc=50, scale=7, size=1000),"poisson": random.poisson(lam=50, size=1000)
}sns.displot(data, kind="kde")plt.show() 
二项分布vs泊松分布
二项分布只有两种可能的结果,而泊松分布可以有无限种可能的结果。但是对于非常大n且接近于零的p二项分布几乎与泊松分布相同,因此n * p几乎等于lam。
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snsdata = {"binomial": random.binomial(n=1000, p=0.01, size=1000),"poisson": random.poisson(lam=10, size=1000)
}sns.displot(data, kind="kde")plt.show()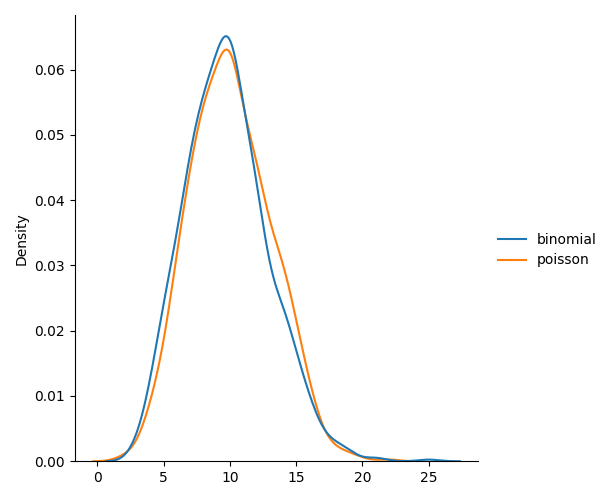
4、均匀分布
用于描述每个事件发生的可能性均等的概率。例如生成随机数。
它有三个参数:
low- 下限 - 默认 0.0。
high- 上限 - 默认 1.0。
size- 返回数组的形状。
例:创建 2x3 均匀分布样本:
from numpy import randomx = random.uniform(size=(2, 3))print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.uniform(size=1000), kind="kde")plt.show()
5、逻辑分布
逻辑分布用于描述增长。广泛应用于逻辑回归、神经网络等机器学习中。
它有三个参数:
loc- 平均值,峰值所在位置。默认值为 0。
scale- 标准差,分布的平坦度。默认值为 1。
size- 返回数组的形状。
例:从均值为 1、标准差为 2.0 的逻辑分布中抽取 2x3 个样本:
from numpy import randomx = random.logistic(loc=1, scale=2, size=(2, 3))print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.logistic(size=1000), kind="kde")plt.show() 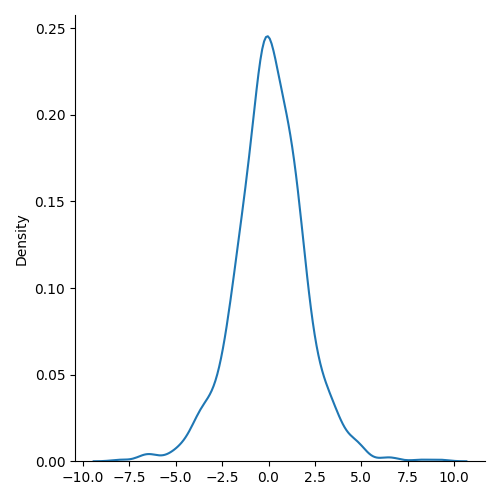
逻辑分布vs正态分布
两种分布几乎相同,但逻辑分布的尾部面积更大,这意味着它表示远离平均值的事件发生的可能性更大。对于较高的尺度值(标准差),除峰值外,正态分布和逻辑分布几乎相同。
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snsdata = {"normal": random.normal(scale=2, size=1000),"logistic": random.logistic(size=1000)
}sns.displot(data, kind="kde")plt.show()
6、多项分布
多项分布是二项分布的推广。它描述多项式情景的结果,而二项式情景的结果只能是两者之一。例如,人群的血型、掷骰子的结果。
它有三个参数:
n- 运行实验的次数。
pvals- 结果概率列表(例如掷骰子的概率为 [1/6, 1/6, 1/6, 1/6, 1/6, 1/6])。
size- 返回数组的形状。
例:抽取一个掷骰子的样本:
from numpy import randomx = random.multinomial(n=6, pvals=[1/6, 1/6, 1/6, 1/6, 1/6, 1/6])print(x)注意:多项式样本不会产生单个值!它们会为每个样本分别产生一个值pval。
注意:由于它们是二项分布的概括,因此它们的视觉表示和正态分布的相似性与多个二项分布相同。
7、指数分布
指数分布用于描述距离下一个事件(例如失败/成功等)的时间。
它有两个参数:
scale- 速率的倒数(参见泊松分布中的 lam)默认为 1.0。
size- 返回数组的形状。
例:绘制一个尺度为 2.0、大小为 2x3 的指数分布样本:
from numpy import randomx = random.exponential(scale=2, size=(2, 3))print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.exponential(size=1000), kind="kde")plt.show() 
泊松分布vs指数分布
泊松分布处理一段时间内事件发生的次数,而指数分布处理这些事件之间的时间。
8、卡方分布
卡方分布作为验证假设的基础。
它有两个参数:
df-(自由度)。
size- 返回数组的形状。
例:绘制一个自由度为 2、大小为 2x3 的卡方分布样本:
from numpy import randomx = random.chisquare(df=2, size=(2, 3))print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.chisquare(df=1, size=1000), kind="kde")plt.show() 
9、瑞利分布
瑞利分布用于信号处理。
它有两个参数:
scale-(标准差)决定分布的平坦程度(默认值为 1.0)。
size- 返回数组的形状。
例:抽取尺度为 2、大小为 2x3 的瑞利分布样本:
from numpy import randomx = random.rayleigh(scale=2, size=(2, 3))print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.rayleigh(size=1000), kind="kde")plt.show()
瑞利分布与卡方分布相似性
在单位标准差和 2 个自由度处,瑞利分布和卡方分布代表相同的分布。
10、帕累托分布
遵循帕累托定律的分布,即 80-20 分布(20% 的因素导致 80% 的结果)。
它有两个参数:
a- 形状参数。
size- 返回数组的形状。
例:绘制一个形状为 2、大小为 2x3 的帕累托分布样本:
from numpy import randomx = random.pareto(a=2, size=(2, 3))print(x)可视化
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.displot(random.pareto(a=2, size=1000))plt.show() 
11、zipf分布
Zipf 分布用于根据 Zipf 定律对数据进行采样。
Zipf 定律: 在一个集合中,第 n 个常见词是出现次数最多的词的 1/n 倍。例如,英语中第 5 个最常见单词的出现次数几乎是出现次数最多的单词的 1/5 倍。
它有两个参数:
a- 分布参数。
size- 返回数组的形状。
例:绘制一个分布参数为 2、大小为 2x3 的 zipf 分布样本:
from numpy import randomx = random.zipf(a=2, size=(2, 3))print(x)可视化
采样 1000 个点,但仅绘制值 < 10 的点以获得更有意义的图表。
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snsx = random.zipf(a=2, size=1000)
sns.displot(x[x<10])plt.show()
