大连理工大学选修课——图形学:第六章 三维变换和三维观察
第六章 三维变换和三维观察
基本三维变换
三维齐次坐标变换矩阵
p ′ = [ x ′ y ′ z ′ 1 ] = p ⋅ T 3 D = [ x y z 1 ] ⋅ [ a b c p d e f q h i j r l m n s ] p'=[x'\ y'\ z'\ 1] = p\cdot T_{3D} = [x\ y\ z\ 1]\cdot \begin{bmatrix} a & b & c & p \\ d & e & f & q\\ h & i & j & r\\ l & m & n & s\\ \end{bmatrix} p′=[x′ y′ z′ 1]=p⋅T3D=[x y z 1]⋅ adhlbeimcfjnpqrs
- 三维集合变换都是相对于坐标原点和坐标轴进行的几何变换。
- 假设变换前一点为 p ( x , y , z ) p(x,y,z) p(x,y,z),变换后为 p ′ ( x ′ , y ′ , z ′ ) p'(x',y',z') p′(x′,y′,z′)。
基本几何变换——平移变换
$T_t =
\begin{bmatrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
T_x & T_y & T_z & 0\
\end{bmatrix}$
基本几何变换——比例变换
-
一般比例变换
T s = [ a 0 0 0 0 e 0 0 0 0 j 0 0 0 0 1 ] T_s = \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & e & 0 & 0 \\ 0 & 0 & j & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} Ts= a0000e0000j00001 -
整体比例变换
T s = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 s ] T_s = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & s\\ \end{bmatrix} Ts= 100001000010000s
基本几何变换——旋转变换
-
绕Z轴旋转
T R Z = [ cos θ sin θ 0 0 − sin θ cos θ 0 0 0 0 1 0 0 0 0 1 ] T_{RZ}= \begin{bmatrix} \cos\theta & \sin\theta & 0 & 0\\ -\sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TRZ= cosθ−sinθ00sinθcosθ0000100001 -
绕X轴旋转
T R X = [ 1 0 0 0 0 cos θ sin θ 0 0 − sin θ cos θ 0 0 0 0 1 ] T_{RX} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos\theta & \sin\theta & 0\\ 0 & -\sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} TRX= 10000cosθ−sinθ00sinθcosθ00001 -
绕Y轴旋转
T R X = [ cos θ 0 − sin θ 0 0 1 0 0 sin θ 0 cos θ 0 0 0 0 1 ] T_{RX} = \begin{bmatrix} \cos\theta & 0 & -\sin\theta & 0\\ 0 & 1 & 0 & 0\\ \sin\theta & 0 & \cos\theta & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} TRX= cosθ0sinθ00100−sinθ0cosθ00001 
基本几何变换——对称变换
- 关于坐标平面对称
- 关于XOY平面对称:
T F x y = [ 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 1 ] T_{F_{xy}}=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFxy= 1000010000−100001 - 关于YOZ平面对称:
T F y z = [ − 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] T_{F_{yz}}=\begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFyz= −1000010000100001 - 关于ZOX平面对称:
T F z x = [ 1 0 0 0 0 − 1 0 0 0 0 1 0 0 0 0 1 ] T_{F_{zx}}=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFzx= 10000−10000100001
- 关于XOY平面对称:
- 关于坐标轴对称
- 关于x轴对称:
T F x = [ 1 0 0 0 0 − 1 0 0 0 0 − 1 0 0 0 0 1 ] T_{F_{x}}=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFx= 10000−10000−100001 - 关于y轴对称:
T F y = [ − 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 1 ] T_{F_{y}}=\begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFy= −1000010000−100001 - 关于z轴对称:
T F z = [ − 1 0 0 0 0 − 1 0 0 0 0 1 0 0 0 0 1 ] T_{F_{z}}=\begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFz= −10000−10000100001
- 关于x轴对称:
- 关于原点对称:
T F o = [ − 1 0 0 0 0 − 1 0 0 0 0 − 1 0 0 0 0 1 ] T_{F_{o}}=\begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TFo= −10000−10000−100001
基本几何变换——错切变换
T S H = [ 1 b c 0 d 1 f 0 g h 1 0 0 0 0 1 ] T_{SH}=\begin{bmatrix} 1 & b & c & 0\\ d & 1 & f & 0\\ g & h & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} TSH= 1dg0b1h0cf100001
逆变换
与上述变换过程相反的变换
-
平移的逆变换
T t − 1 = [ 1 0 0 0 0 1 0 0 0 0 1 0 − T x − T y − T z 0 ] T_t^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -T_x & -T_y & -T_z & 0\\ \end{bmatrix} Tt−1= 100−Tx010−Ty001−Tz0000 -
比例的逆变换
T s − 1 = [ 1 a 0 0 0 0 1 e 0 0 0 0 1 j 0 0 0 0 1 ] T_s^{-1} = \begin{bmatrix} \frac{1}{a} & 0 & 0 & 0 \\ 0 & \frac{1}{e} & 0 & 0 \\ 0 & 0 & \frac{1}{j} & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} Ts−1= a10000e10000j100001 -
整体比例变换的逆变换
T s − 1 = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 s ] T_s^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & \frac{1}{s}\\ \end{bmatrix} Ts−1= 100001000010000s1 -
旋转的逆变换
$T_{RZ}^{-1}=
\begin{bmatrix}
\cos(-\theta) & \sin(-\theta) & 0 & 0\
-\sin(-\theta) & \cos(-\theta) & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 1\
\end{bmatrix}\begin{bmatrix}
\cos\theta & -\sin\theta & 0 & 0\
\sin\theta & \cos\theta & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 1\
\end{bmatrix}$
三维复合变换
- 图形作一次以上的变换
- 变换结果为每次变换矩阵的乘积
P ′ = P ⋅ T = P ⋅ ( T 1 ⋅ T 2 ⋯ T n ) ( n > 1 ) P'=P\cdot T = P\cdot(T_1\cdot T_2\cdots T_n)(n>1) P′=P⋅T=P⋅(T1⋅T2⋯Tn)(n>1) - 相对于参考点 F ( x f , y f , z f ) F(x_f,y_f,z_f) F(xf,yf,zf)作比例、对称等变换步骤:
- 将参考点F移动至坐标原点
- 进行三维几何变换
- 反平移

绕任意轴的三维旋转变换




- 类似地,针对任意方向轴的变换步骤为
- 将起点与坐标原点重合,即进行平移变换。
- 使方向轴与某一坐标轴重合,即进行旋转变换,可能不止一次。
- 完成基本变换。
- 逆旋转变换。
- 逆平移变换。
三维几何变换
投影变换
定义: 把三维立体(或物体)投影得到二维平面图形的过程
包括:平行投影、透视投影、以及通过这些变换得到的三视图、轴测图、透视图。
投影构成:投影中心、投影面、投影线。

透视投影、平行投影(包括正投影、斜投影)
-
透视投影的投影中心到投影面的距离有限
-
平行投影的投影中心到投影面的距离无限

分类:

平行投影
-
可分为两类:正投影和斜投影。

-
性质:能够精确反应物体实际尺寸。
正投影
-
正投影分为:三视图和正轴测。
- 当投影面与某一坐标轴垂直时,得到的为三视图,否则为正轴测图。

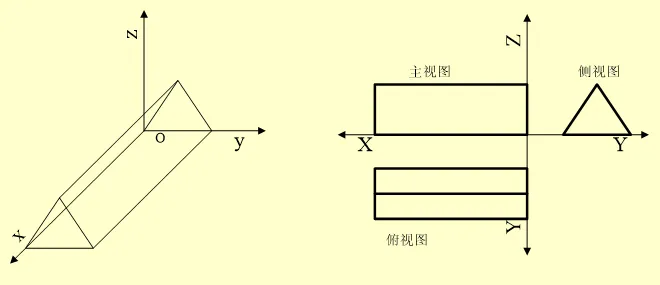
正投影——三视图
-
三视图包括:主视图、侧视图、俯视图三种,投影面分别与Y、X、Z轴垂直。

-
步骤:
- 确定三维形体各点位置坐标。
- 引入齐次坐标,求出对应变换矩阵。
- 将引入的变换用矩阵表示,通过运算求得形体上各点 ( x , y , z ) (x,\ y,\ z) (x, y, z)经过变换后的相应点 ( x ′ , y ′ ) (x',\ y') (x′, y′)或 ( y ′ , z ′ ) (y',\ z') (y′, z′)或 ( z ′ , x ′ ) (z',\ x') (z′, x′)。
- 用得到的二维点绘制三视图。
-
主视图投影矩阵为:
T v = [ 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 ] T_v = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} Tv= 1000000000100001
-
俯视图投影矩阵为:
T = T x o y ⋅ T R x ⋅ T t z = [ 1 0 0 0 0 0 − 1 0 0 0 0 0 0 0 − z 0 1 ] T = T_{xoy}\cdot T_{Rx}\cdot T_{tz} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & -z_0 & 1\\ \end{bmatrix} T=Txoy⋅TRx⋅Ttz= 100000000−10−z00001 -
侧视图投影矩阵为:
T = T y o z ⋅ T R z ⋅ T t = [ 0 0 0 0 − 1 0 0 0 0 0 1 0 − x 0 0 0 1 ] T = T_{yoz}\cdot T_{Rz}\cdot T_{t} = \begin{bmatrix} 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ -x_0 & 0 & 0 & 1\\ \end{bmatrix} T=Tyoz⋅TRz⋅Tt= 0−10−x0000000100001 -
最后可以得到三视图为:
正投影——正轴测
-
图例:

-
正轴测投影变换矩阵
T = T R y ⋅ T R x ⋅ T p = [ cos α − sin α ⋅ sin β 0 0 0 cos β 0 0 − sin α − cos α ⋅ sin β 0 0 0 0 0 1 ] T = T_{Ry}\cdot T_{Rx}\cdot T_{p} = \begin{bmatrix} \cos\alpha & -\sin\alpha\cdot\sin\beta & 0 & 0\\ 0 & \cos\beta & 0 & 0\\ -\sin\alpha & -\cos\alpha\cdot\sin\beta & 0 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} T=TRy⋅TRx⋅Tp= cosα0−sinα0−sinα⋅sinβcosβ−cosα⋅sinβ000000001
该矩阵是一般正轴测图的投影变换矩阵。 -
正等测图参数:
- sin α = cos α = 2 2 \sin\alpha = \cos\alpha = \frac{\sqrt2}{2} sinα=cosα=22
- sin β = 3 3 \sin\beta = \frac{\sqrt 3}{3} sinβ=33
- cos β = 6 3 \cos\beta = \frac{\sqrt 6}{3} cosβ=36
-
正二测图参数:
- sin α = cos α = 2 2 \sin\alpha = \cos\alpha = \frac{\sqrt 2}{2} sinα=cosα=22
-
正轴测图特点:
- 能同时反映物体的多个面,具有一定的立体效果。
- 空间任意一组平行线的投影仍然保持平行。
- 不能保持三维空间的角度关系。
- 沿三个坐标轴的方向均可测量距离,但要注意比例关系。
斜投影
即斜轴测图。
将三维形体向一个单一的投影面作平行投影。
投影方向不垂直于投影面所得到的平面图形。
- 常选用垂直于某个主轴的投影面。
- 使得平行于投影面的形体表面可以进行距离和角度的测量。
- 特点
- 既可以进行测量又可以同时反映三维形体的多个面。
- 具有立体效果。
- 常用的斜轴测图有斜等测图和斜二测图。


- 斜平行投影的投影变换矩阵为:
T = [ 1 0 0 0 0 1 0 0 c t g α cos β c t g α sin β 0 0 0 0 0 1 ] T = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ ctg\alpha\cos\beta& ctg\alpha\sin\beta& 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} T= 10ctgαcosβ001ctgαsinβ000000001 - 对于斜等测图: α = 45 ° , c t g α = 1 \alpha = 45\degree, ctg\alpha = 1 α=45°,ctgα=1。
- 对于斜二侧图: α = a r c t g ( 2 ) , c t g α = 1 2 , β 通常取 30 ° 或 45 ° 。 \alpha=arctg(2),ctg\alpha=\frac{1}{2},\beta通常取30\degree或45\degree。 α=arctg(2),ctgα=21,β通常取30°或45°。

透视投影
$\begin{bmatrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 0 & \frac{1}{d}\
0 & 0 & 0 & 1\
\end{bmatrix}$

- 透视缩小效应:物体的透视投影的大小与物体到投影中心的Z方向距离成反比。

-
透视投影特点
- 深度感更强,更加具有真实感,但不能够准确反映物体的大小和形状。
- 大小与物体到投影中心的距离有关。
- 一组平行线若平行于投影平面时,透视投影仍然保持平行。
- 当物体表面平行于投影平面时,该表面上的角度在透视投影中才能被保持。
-
灭点:不平行于投影面的平行线的投影汇聚到的一个点。
-
主灭点:坐标轴方向的平行线在投影面上形成的灭点。
-
一点透视有一个主灭点,即投影面与一个坐标轴正交,与另外两个坐标轴平行。
-
两点透视有两个主灭点,即投影面与两个坐标轴相交,与另一个坐标轴平行。
-
三点透视有三个主灭点,即投影面与三个坐标轴都相交。

-
-
透视投影变换矩阵:
[ 1 0 0 p 0 1 0 q 0 0 1 r 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & p\\ 0 & 1 & 0 & q\\ 0 & 0 & 1 & r\\ 0 & 0 & 0 & 1\\ \end{bmatrix} 100001000010pqr1
三维观察
观察坐标系
-
观察参考点
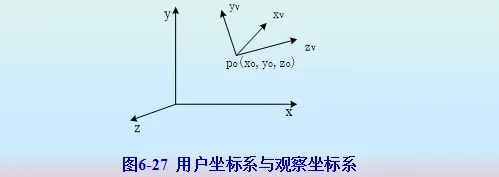
-
观察平面,即投影平面。

-
通过改变观察参考点的位置或改变N的方向可以使用户在不同的距离和角度观察三维形体

-
观察窗口:属于观察平面内。

观察空间
定义:将观察窗口沿投影方向作平移运动产生的三维形体

观察空间分为:无限观察空间、有限观察空间。
前后截面:Zfront,Zback。

- 对于透视投影,前截面必须在投影中心和后截面之间。
- 观察平面和前后截面的有关位置取决于要生成的窗口类型及特殊图形包的限制。

- 规范化观察空间
-
平行投影的规范化观察空间定义:
$x_v = 1, x_v = -1\
y_v = 1, y_v = -1\
z_v = 0, z_v = 1\$ -
透视投影的规范化观察空间定义:
$x_v = z_v, x_v = -z_v\
y_v = z_v, y_v = -z_v\
z_v = z_{min},z_v = 1\$
-


三维观察流程
应用程序→用户坐标→观察坐标系→规范化投影坐标→规范化二维坐标→输出
观察坐标系到用户坐标系
- 具体变换步骤
- 平移观察参考点到用户坐标系原点。
- 旋转,让 x v , y v , z v 对应到用户坐标系的 x , y , z 轴 x_v,y_v,z_v对应到用户坐标系的x,y,z轴 xv,yv,zv对应到用户坐标系的x,y,z轴。



平行投影的规范化投影变换
- 观察窗口:左下角点(xwmin,ywmin),右上角点( xwmax,ywmax )。
- 参考点:(xprp,yprp,zprp)。
- 前后截面:Z=Zfront,Z=Zback。
- 观察平面:Z=Zvp
- 投影方向为从参考点到观察窗口中心点的坐标矢量。
- 分为以下三步骤:
-
将投影中心平移到观察坐标系原点。

-
对坐标系进行错切变换,使参考点和窗口中心的连线错切到zv轴。
变换后窗口中心点的坐标为:
x c w = ( x w m i n + x w m a x / 2 − x p r p ) y c w = ( y w m i n + y w m a x / 2 − y p r p ) z c w = z v p − z p r p x_{cw}=(xw_{min}+xw_{max}/2-x_{prp})\\ y_cw = (yw_{min} + yw_{max}/2 -y_{prp})\\ z_{cw} = z_{vp}-z_{prp} xcw=(xwmin+xwmax/2−xprp)ycw=(ywmin+ywmax/2−yprp)zcw=zvp−zprp
解得: a = − x c w z c w , b = − y c w z c w a = \frac{-x_{cw}}{z_{cw}}, b = \frac{-y_{cw}}{z_{cw}} a=zcw−xcw,b=zcw−ycw

-
进行坐标的归一化变换

-
平移变换

-
比例变换

-
-
透视投影的规范化投影变换
分为两步:
- 平移

- 错切、比例

- 观察窗口:左下角点(xwmin,ywmin),右上角点( xwmax,ywmax )。
- 参考点:(xprp,yprp,zprp)。
- 前后截面:Z=Zfront,Z=Zback。
- 观察平面:Z=Zvp
- 变换步骤:
- 将投影中心平移到观察坐标系原点。
- 对坐标系进行错切变换。

3. 进行比例变换

三维裁剪
定义:保留所有在观察空间内的图形以便在输出设备中显示,所有在观察空间外的图形被丢弃。
- 四维齐次坐标表示的图形裁剪:
- 将齐次坐标转换为三维坐标,在三维空间中关于规范化观察空间裁剪。
- 直接在齐次坐标空间中进行裁剪。
