当前位置：首页 > news >正文

实验三触发器及基本时序电路

news 2025/5/5 5:55:54

1.触发器的分类？各自的特点是什么？

1 、 D 触发器

特点：只有一个数据输入端 D ，在时钟脉冲的触发沿，输出 Q 的状态跟随输入端 D 的状态变化，即 $Q^{n+1}=D$ ，功能直观，利于理解和感受。

2 、 JK 触发器

特点：功能强大，具有两个数据输入端 J 和 K ，能实现置 0 、置 1 、保持和翻转四种功能。当J=0 ， K=0 时，保持原状态； J=0 ， K=1 时置 0 ； J=1 ， K=0 时置 1 ； J=1 ， K=1 时实现状态翻转，功能灵活多样，表达式为 $Q^{n+1}=J\overline{Q^{n}}+\overline{K}Q^{n}$ 。

3 、 T 触发器

特点：只有一个输入端 T ，当 T=0 时，触发器保持原状态；当 T=1 时触发器在时钟脉冲的触发沿发生状态翻转即 $Q^{n+1}=\overline{Q^{n}}$ ，这种状态翻转的特性使其在一些需要对信号进行二分频或实现特定计数功能的电路中非常有用，其表达式为 $Q^{n+1}=T\bigotimes Q^{n}$ 。

2.设计同步时序电路

用JK触发器设计模为九的二进制减法计数器：

一、状态转换图

模 9 计数器是指在时钟信号作用下，计数器状态从 8 开始，每次时钟脉冲从到来时状态减一，当计数到 0 时，下一个时钟状态回到八，形成一个包含 9 个状态的循环，实现模 9 的减法计数功能，当第一个 CP 到来时产生借位， Y 输出为 1 。

二、状态转换真值表

三、确定触发器数量和类型

由于要实现的是模为 9 的二进制减法计数器一共需要九个状态，所以需要四个触发器，本次实验中

采用的触发器是 JK 触发器。

四、求激励函数和输出函数

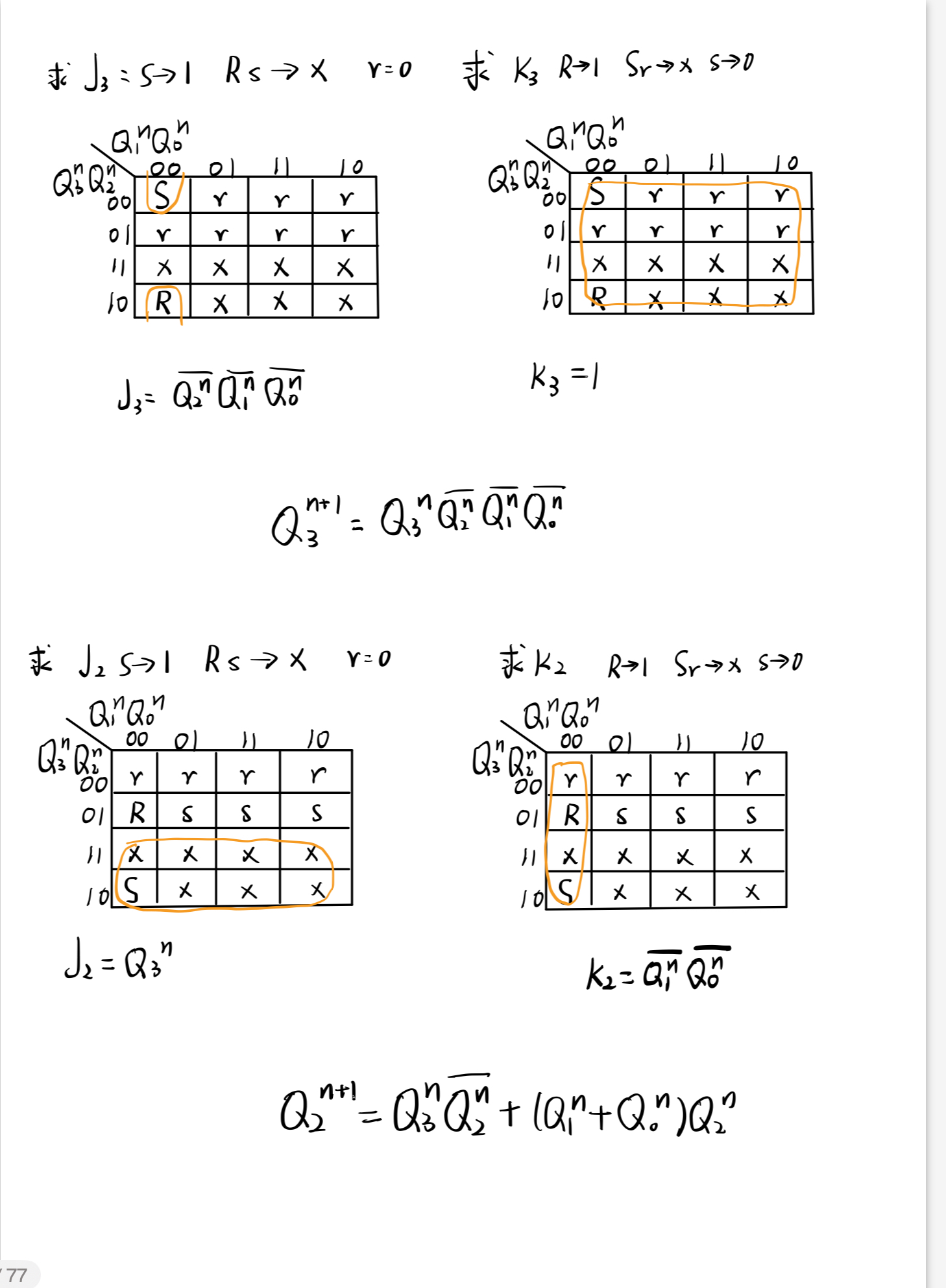
有上述计算结果可知各激励函数分别为 $Q_{3}^{n+1}=Q_{3}^{n}\overline{Q_{2}^{n}}\overline{Q_{1}^{n}}\overline{Q_{0}^{n}}$ ,

$Q_{2}^{n+1}=Q_{3}^{n}\overline{Q_{2}^{n}}+(Q_{1}^{n}+Q_{0}^{n})Q_{2}^{n}$ , $Q_{1}^{n+1}=(Q_{2}^{n}\overline{Q_{0}^{n}}+Q_{3}^{n})\overline{Q_{1}^{n}}+Q_{0}^{n}Q_{1}^{n}$ ,

$Q_{0}^{n+1}=(Q_{2}^{n}+Q_{3}^{n}+Q_{1}^{n})\overline{Q_{0}^{n}}$ ,输出函数 $Y=\overline{Q_{0}^{n}}\overline{Q_{1}^{n}}\overline{Q_{2}^{n}}\overline{Q_{3}^{n}}$

五、逻辑电路图

六、结果分析

由上述图中的波形图结果可知，当 $Q_{3}^{n}Q_{2}^{n}Q_{1}^{n}Q_{0}^{n}=0000$ 时 $Y=1$ 表示向借位，之后经过 9 个

CP $Q_{3}^{n}Q_{2}^{n}Q_{1}^{n}Q_{0}^{n}$ 的状态从 0000 到下一状态 1000 再依次减到 0000 ，只有当第一个

CP 到来时 Y 输出为 1 ，其余状态输出为 0 。

七、判断自启动

由各激励函数的表达式： $Q_{3}^{n+1}=Q_{3}^{n}\overline{Q_{2}^{n}}\overline{Q_{1}^{n}}\overline{Q_{0}^{n}}$ ， $Q_{2}^{n+1}=Q_{3}^{n}\overline{Q_{2}^{n}}+(Q_{1}^{n}+Q_{0}^{n})Q_{2}^{n}$ ，

$Q_{1}^{n+1}=(Q_{2}^{n}\overline{Q_{0}^{n}}+Q_{3}^{n})\overline{Q_{1}^{n}}+Q_{0}^{n}Q_{1}^{n}$ ， $Q_{0}^{n+1}=(Q_{2}^{n}+Q_{3}^{n}+Q_{1}^{n})\overline{Q_{0}^{n}}$ ，可以算出剩下状态的下一状态情况，如下图计算结果所示。