人工智能发展史 — 物理学诺奖之 Hopfield 联想和记忆神经网络模型

目录

1982 年，Hopfield 联想和记忆神经网络模型

1982 年，约翰·霍普菲尔德（John Hopfield）通过对生物大脑的联想记忆机制进行了研究，发表论文《神经网络和具有突发性集体计算能力的物理系统》，提出了一种全互联反馈神经网络数学模型，即：Hopfield 神经网络模型。此模型尝试解释神经网络系统如何存储记忆，又是如何从海量记忆中快速联想某个记忆片段。

Hopfield 神经网络模仿了生物大脑的联想记忆功能，通过物理学能量函数最小化模拟了大脑的信息存储和检索能力，被应用于图像识别等场景，例如：通过 Hopfield 神经网络 “记忆” 存储了一张图片的数据之后，就可以通过 “联想” 能力来修复这张 “破损” 的图片。

背景知识

历史：霍普菲尔德简介

约翰·霍普菲尔德（John Hopfield）文学士、物理学博士，研究领域横跨物理学、分子生物学、神经科学、计算机科学，是一名以推动跨学科交叉融合而闻名于世的科学家，其推动了物理学与生命科学、人工智能的交叉融合，被誉为 “扩展统计物理学边界的先驱”，获得了 2024 年的物理学诺贝尔奖。

霍普菲尔德早期是理论物理学家，专注于固体物理和量子力学，研究电子行为与能量状态，在激化子、长程电子输运等方面有极大的贡献。然而，20 世纪 70 年代，他对生物学和神经科学产生了浓厚兴趣，尤其是大脑如何存储和处理信息的问题。

他在贝尔实验室期间参与了跨学科研讨会，与神经科学家合作探讨神经网络与生物学的联系，这种交流促使他将物理学原理应用到生物系统中。

• 1979 年，贝尔实验室的跨学科研讨会：霍普菲尔德与生物学家讨论神经网络的可能机制，开始尝试用数学模型解释大脑的信息处理。
• 1981 年，普林斯顿大学神经科学会议：大卫·马尔（David Marr）关于视觉系统如何组织信息的演讲，启发霍普菲尔德将物理系统的自组织特性与神经网络结合。

得益于与好友 Phil Anderson（凝聚态理论物理学家，1977 年诺贝尔奖得主）长期交流，霍普菲尔德对自旋玻璃理论进行了深入的研究。最终在 1982 年提出了 Hopfield 神经网络模型。

因此，在 Hopfield 神经网络中，我们将看见物理学、神经科学、计算机学科三者之间的交汇融合。（注意，本文中只讨论离散型 Hopfield 神经网络。）

神经学：大脑的联想记忆机制

生物大脑的 “联想记忆” 指的是，当我们听见一首音乐的片段时，我们可以回想起歌词并唱出来，而不需要听完整首歌曲才能记起。当我们看见一张模糊的甚至是残缺的照片时，我们可以回想起照片的全貌，而不需要看见完整的照片。

生物大脑的联想记忆由海马体和杏仁核等多个脑区协作，并通过突触可塑性和神经网络的动态同步来实现。具体而言：

1. 海马体的记忆巩固：海马体负责将短期记忆转化为长期记忆。其中 CA3 区通过 “模式分离（区分相似记忆）” 和 “模式完成（从部分信息恢复完整记忆）” 实现联想记忆 。例如：当接收到部分感官输入时，海马体能够激活与之相关的完整记忆模式。
2. 杏仁核的情绪记忆整合：杏仁核将情绪信息（如恐惧或快乐）与感官输入绑定，形成带有情感色彩的联想记忆。例如：闻到某种气味可能触发与特定情绪事件相关的记忆 。
3. 突触可塑性：赫布定律解释了重复的神经活动会强化并塑造相关的突触连接，形成记忆痕迹。长期增强（LTP）和长期抑制（LTD）是生物联想记忆的基础。
4. 神经网络的动态同步：神经元集群通过同步放电编码和检索记忆。这种时空编码方式允许大脑从噪声或部分输入中恢复完整信息。

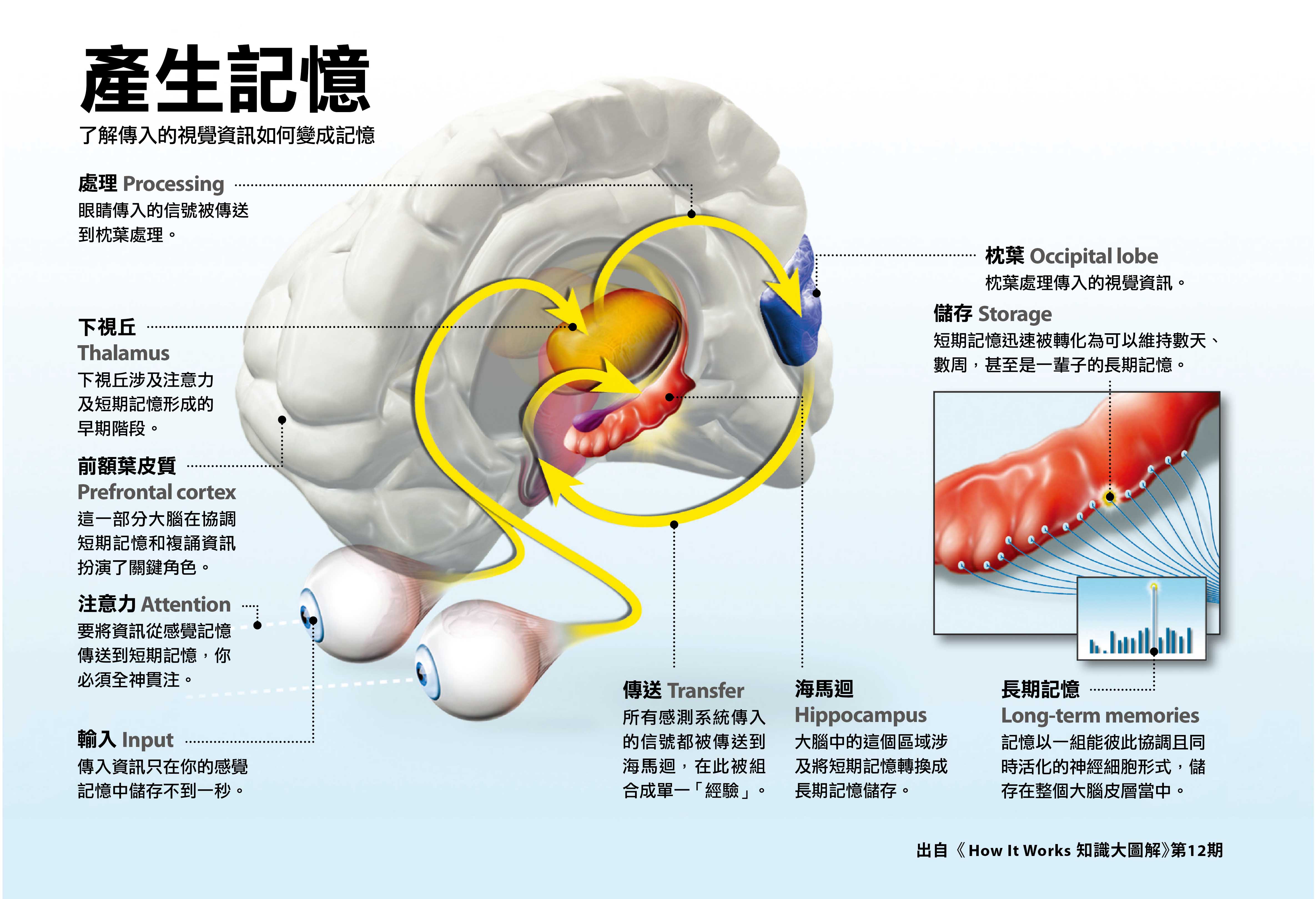
联想记忆功能可以被抽象为下图这般的神经动力学：空间中任何一个点都代表大脑可能的一个状态，每一个吸引子（黑点）编码了一份记忆，同时这些吸引子把整个空间划分成了各自的吸引域，如果大脑状态落进了某个吸引域就相当于是拥有了一些辅助信息，之后会被吸引到相应的吸引子那里，这个吸引的过程就是联想或者说找回记忆（memory retrieval，pattern completion）的过程。

Hopfield 神经网络正是为构造上图这样的动力学系统提供了一个简单的模型。

物理学：磁性材料的自旋玻璃理论和能量最小值函数

霍普菲尔德早年从事磁性材料的自旋玻璃的研究。自旋玻璃（Spin Glass）是磁性材料的一种原子自旋性质，而不是一种 “玻璃”。

磁性材料的每颗原子都相当于一个小磁铁，邻近原子之间的自旋会互相影响，使得自旋方向一致的区域（非全局）形成。以下是自旋玻璃的关键特性：

1. 阻挫（Frustration）性质：想象一群人（磁矩，如下图红蓝箭头）在黑暗中随机站立，每个人可以选择面朝东或西（自旋方向，红箭头或蓝箭头）。若规则是 “邻居必须面朝同一方向”（铁磁相变），所有人会整齐排列；若规则是 “邻居必须相反方向”（反铁磁相变），则形成交替排列。但自旋玻璃的规则是混合的（自旋玻璃相变），即：某些邻居必须同向，另一些则必须反向，导致无法达成统一，陷入混乱的 “争执” 状态，称为阻挫。
2. 自旋冻结性质：高温时，磁矩的自旋方向会随机翻转（像沸腾的水）；降温后，磁矩的自旋方向会具有无序性，并需要长时间才能逐渐稳定下来（朝能量最小的方向稳定，符合热力学第二定律），就类似于高温融化的玻璃逐渐冷却固化的过程。因此得名 “自旋玻璃”。
3. 亚稳态多样性质：冷却固化后，磁性系统系统通过磁矩相互作用达到了能量最小化的亚稳态（局部能量极小值），并呈现出亚稳态的多样性，即：系统可能稳定在多个能量相近但结构不同的亚稳态中，而非唯一的一个全局最低能量态。所有的能量亚稳态可能性被描绘在一张 “多谷结构的能量景观” 中，每个山谷代表一种可能的亚稳态。

自旋玻璃的亚稳态（局部能力极小值）通过能量最小函数（Energy Minimization Function）来计算。能量最小函数是一种用于描述动态系统稳定性的数学工具，其核心思想是系统在演化过程中会自发向能量最低的状态收敛。

自旋玻璃的能量函数如下所示，J_ij 是自旋间的相互作用强度，S_i 是自旋方向（±1，红蓝箭头）。

Hopfield 神经网络基本原理

大脑的记忆和联想就相当于计算机中的存储和检索。对此，最直观的思路就是构建一个庞大的 “数据库” 将信息存储下来，然后通过 “最长匹配优先” 等算法来进行检索。但是人工神经元不是计算机，也没有数据库，如何实现 “存储空间如何足够大” 和 “检索速度如何足够快” 的最优解问题呢？

霍普菲尔德突破了常规的思维，他从热力学和物理学中获得灵感，认为 “能量最小化原则” 就是自然界中最优的路径，可用于神经网络寻找最优解的过程，继而基于 “能量最小化函数” 来模拟了神经网络中的记忆和联想。

Hopfield 神经网络展示了在神经网络中如何通过能量极小点和来存储和检索记忆，具有深刻的物理含义。

记忆存储（训练），构建能量景观用于存储不同的模式

1. 首先，神经网络接受图片的二值化矩阵向量输入（对神经元进行 +/-1 赋值）；
2. 然后，基于 “能量最小化原则” 通过计算出神经网络的能量总和值；
3. 接着，根据 Hebbian 学习规则来训练网络的权重参数，确保系统在迭代过程中能量严格递减，最终稳定在局部或全局最小值点。
4. 最后，训练收敛，神经网络系统到达了能量最小化的亚稳态，完成了对图片的储存（“记忆” 过程）。并且每个亚稳态对应存储一个记忆模式，多个亚稳态可以存储多个记忆模式（多张图片）。

联想检索（推理），系统状态的动态变化朝着局部最小值发展

在神经元连接权重确定的前提下，神经网络通过调整神经元的数值来使得能量变化。例如：当一张新的图片被输入到网络时，新图片对应的神经元的数值都会逐一被检查。根据能量最小化函数，如果存在 “破损” 部分，那么改变破损神经元的数值可以让网络的能量总和继续下降（“联想” 过程），然后就会修改这个神经元的数值（图片修复过程）。

数学模型的元素

霍普菲尔德认为磁性原子集群和神经元集群拥有类似的 “互相动态影响” 集群行为，所以 Hopfield 神经网络具有特殊的网络拓扑结构，所有节点之间相互全连接。模拟了生物神经元相互连接，如下图所示。

在这个全连接反馈网络中，每个神经元既有输入也有输出，且每个神经元的输出就作为其他神经元的输入。通过连接形成一个动态系统，模拟了大脑中神经元集群的递归循环活动。

受到统计物理学 Ising 铁磁模型启发，Hopfield 神经网络中的神经元集群具有以下特性：

1. 都有一个 x_i 状态，且只有 2 种可能的取值，代表神经元处于活跃或不活跃状态。（注：离散型 Hopfield 网络中，所有神经元的取值都是 -1 或 +1，而不是一个连续的值。）

   • 激活 x_i = +1
   • 未激活 x_i = -1

2. 每条连接都有一个权重 w_ij。

   • 同态链 w_ij > 0，如其一端的神经元处于激发态，会影响另一端的神经元也处于激发态。如其一端神经元处于未激发态，另一端的神经元也会受到抑制。
   • 异态链 w_ij < 0，则相反，其一端神经元的状态会 “反向地” 影响另一端神经元的状态。
   • 权重对称性 w_ji = w_ji。

3. 2 个神经元之间的能量契合度为：h_ij = w_ij ⋅ x_i ⋅ x_j

   • h_i > 0 为高能契合度。
   • h_i < 0 为低能契合度。

以只有 3 个神经元的 Hopfield 神经网络为例，其图形如下所示：

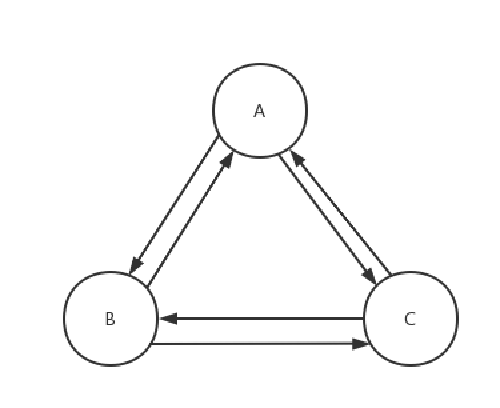
那么上图的权重矩阵就为：

• w_ii = 0 时，神经元不连接自己，所以权重为 0。
• A 不等于 B 时，w_BA = w_AB 对称。
  

神经网络的能量最小函数

整个神经网络的总能量 H 为所有神经元以及之间的权重的累乘积，如下：

• x_i：神经元 i 的激活状态（+1 或 -1）。
• x_j：神经元 j 的激活状态（+1 或 -1）。
• w_ij：神经元 i 与 j 之间的连接权重（需满足对称性，w_ij = w_ji）。

而 Hopfield 神经网络迭代计算的目的就在于求得符合 “能量最小化原则” 的权重矩阵参数。所以最小能量函数 E 就是总能量 H 的负值。这里使用负值，是因为物理学的习惯。这样的系统，低势能才是稳定态。

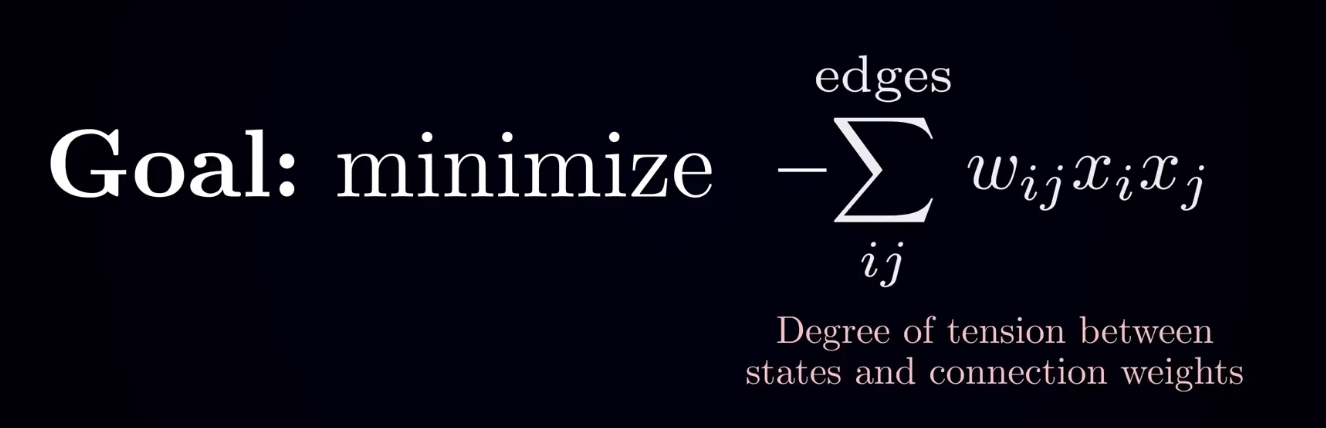
进而，将能力最小函数应用到神经网络中，我们就得到了 Hopfield 神经网络完整的能量最小函数模型，如下图所示。

新记忆的形成：训练中的参数调整迭代

Hopfield 认为神经元的连接权重 w_ij 应当满足 Hebbian 学习规则，以此来进行学习（权重参数调整），模拟了生物神经元突触的可塑性。

Hebb 学习法则指出：当 2 个神经元之间一同激活时，那么它们之间的连接会被加强。所以，得到得到连接权重参数的更新公式，如下图所示。

• Δw_ij 是神经元 i 和 j 之间的权重的变化量。
• η 是学习率，正数，控制权值更新的速度。
• 一个二值化矩阵向量 ξ，其中 ξ_i 表示第 i 个神经元的状态，ξ_j 表示第 j 个神经元的状态（-1 或 +1）。

将公式代入到能量函数中后，得到以下公式。显然的，此时当 ξ_i 和 ξ_j 都是 +1（激活）时，w_ij > 0，此时让 w_ij 变大，则会降低网络的总能量。符合 Hebb 学习法则。

如下公式小于 0。

在训练过程中，调整权重和偏置量参数的几何意义就是在能量景观中 “挖掘” 低谷。

记忆联想算法：推理中的神经元数值调整迭代

对比理解，感知机模型是一种前馈神经网络，推理中用于完成静态的非线性映射；而 Hopfield 模型是一个 “循环/递归/反馈” 神经网络，即：x_i 的输出最终会成为影响 x_i 自身的输入。

同时，Hopfield 模型也是一个反馈动力学系统，其状态演化遵循一个简单的动力学规则，即：对于任意神经元 x_i，其 t+1 时刻的状态由 t 时刻的状态决定。

这使得 Hopfield 网络能够自我调整，恢复到稳定状态。简而言之，推理过程中，Hopfield 神经网络通过动态更新神经元 x_i 的状态，使得网络的能量降低。每次迭代只改变一个神经元的状态，根据顺序逐一更新（进行联想修复），最终使得整个网络的总能量 E 不再降低。

更新公式如下所示：

• s_j(t_n) 是当前时刻第 j 个神经元的状态。
• s_i(t_n+1) 是下一时刻第 i 个神经元的状态。
• J_ij 是 i 和 j 之间的权重。
• 激活函数采用了 sgn 符号函数。
  

该公式的现实意义为：如果一个神经元 i 所连接的 N 个其他神经元及它们之间的权重乘积 > 0，则表示 i 被 “多数投票” 为 +1，否则为 -1。

即：x_i 转换为高能契合，可以提高总能量 H，降低能量最小函数值 E。

记忆多个模式（Pattern）

Hopfield 神经网络可以存储多个模式（图片），但存储容量有限，存储的数量取决于神经元数量的规模，通常是 0.14N 个模式（N 是神经元数量）。

如下是一幅 Hopfield 神经网络的能量景观示意图，每个记忆模式对应着网络中的一个极小值（但不是每个极小值对应一个记忆模式，可能是虚假的记忆）。

多个模式的权重矩阵就等于将全部模式的权重矩阵向量进行叠加。

应用示例

下面以记忆存储和联想修复 2 个 6x6 维的图像为例。

训练图像 1：

• 图像的二值化矩阵为（神经元的数值是通过图片的二值化矩阵向量完成输入的）：
  

• 矩阵可以展开成向量 V：
  V = [0,0,1,1,0,0,0,0,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,0,0,0,0,1,1,0,0]

• 对应的图像为：
  

训练图像 2：

• 图像的二值化矩阵为（神经元的数值是通过图片的二值化矩阵向量完成输入的）：
  

• 矩阵可以展开成向量 V：
  V = [0,0,1,1,0,0,0,1,0,0,1,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,0,0,1,0,0,0,1,1,0,0]

• 对应的图像为：
  

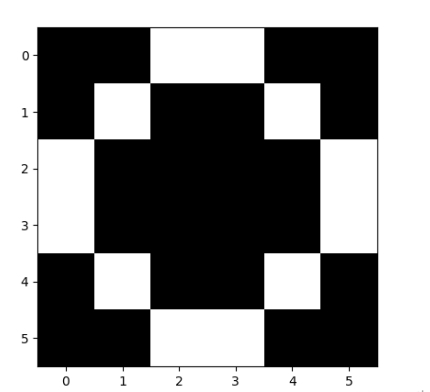
2 个模式存储的结果：

推理修复图形 3：

Python 代码实现：

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt# -------------------------- 定义存储模式 -------------------------- 
# 霍普菲尔德网络中存储的"记忆"模式，这里用6x6二值矩阵表示简单图形
a = np.array([[0,0,1,1,0,0],[0,0,1,1,0,0],[1,1,1,1,1,1],[1,1,1,1,1,1],[0,0,1,1,0,0],[0,0,1,1,0,0]])  # 类似"十字"图形b = np.array([[0,0,1,1,0,0],[0,1,0,0,1,0],[1,0,0,0,0,1],[1,0,0,0,0,1],[0,1,0,0,1,0],[0,0,1,1,0,0]])  # 类似"圆环"图形c = np.array([[0,0,1,1,0,0],[0,0,1,1,0,0],[1,1,1,1,1,1],[1,1,1,1,1,1],[1,0,0,1,0,0],[0,0,1,1,0,0]])  # 被噪声污染的"十字"（用于测试联想记忆）# ------------------------ 霍普菲尔德网络初始化 ------------------------
# 将矩阵展平为向量（霍普菲尔德神经元的状态表示）
array_a = a.flatten()  # 36维向量（6x6=36神经元）
array_b = b.flatten()
input_array = [array_a, array_b]  # 存储的记忆模式集合# 初始化权重矩阵（关键参数，体现Hebbian学习规则）
w = np.zeros((36, 36))  # 36x36权重矩阵（神经元全连接）# 权重训练过程：根据存储模式计算权重矩阵（外积规则）
for s in input_array:w0 = np.zeros((36, 36))for i in range(36):for j in range(36):if i == j:w0[i,j] = 0  # 禁止自连接（霍普菲尔德网络特征）else:# Hebbian学习规则：(2s[i]-1)将0/1转换为-1/1（对称性要求）w0[i,j] = (2*s[i]-1) * (2*s[j]-1)  # 外积公式w += w0  # 累积多个模式的权重# -------------------------- 联想记忆测试 --------------------------
# 初始化输入（带噪声的测试模式）
c = c.flatten()
v0 = c  # 初始状态（受损的输入）# 迭代更新过程（能量最小化搜索）
Y = np.zeros(36)
for t in range(10):  # 迭代次数（通常收敛很快）v1 = np.zeros(36)for j in range(36):  # 对每个神经元j计算输入总和for i in range(36):if i == j:continue  # 跳过自连接else:v1[j] += w[i,j] * v0[i]  # 加权输入求和# 激活函数（阈值判断，对应能量函数的梯度下降）Y[j] = 0 if v1[j] < 0 else 1  # 硬阈值函数v0 = Y  # 更新神经元状态# -------------------------- 结果可视化 --------------------------
# 将结果恢复为二维矩阵并显示
result = np.array(v0).reshape(6, 6)
# 将二值矩阵转为图像（0->0，1->600灰度值）
p = Image.fromarray(result * 600)  
plt.imshow(p)
plt.show()

注意，上述实现中使用了Hebb规则来更新权重，并且在网络状态更新时采用了简单的阈值函数，即 sign 函数。实际应用中，Hopfield 网络还可以采用不同的权重更新规则和激活函数，并且可以根据实际需求调整噪声处理能力和召回性能。在处理大型网络时，应确保对称性权重矩阵的正确性和处理效率。

最终推理修复结果：

局限性

Hopfield 神经网络的一大优点是其强大的联想记忆能力。网络能够通过训练过程存储多个模式，并在接收到与存储模式部分相关的输入时，通过迭代过程自动恢复出完整的模式。这种特性使得 Hopfield 神经网络非常适合应用于图像恢复、序列补全等需要关联记忆的任务。

Hopfield 神经网络的缺点：

1. 易陷入局部极小值：Hopfield网络在迭代过程中寻找能量函数的局部极小值，这意味着网络可能无法在所有情况下都能找到全局最优解，特别是当输入模式非常复杂或者噪声较大时。网络可能在迭代过程中停在了一个并不反映原有存储模式的局部极小点，导致回忆出来的结果不准确或完全错误。

2. 存储容量有限且易发生模式混淆：随着存储模式数量的增加，Hopfield网络的性能会逐渐下降。这是因为网络的权重矩阵必须反映出所有存储模式的信息，过多的模式会导致权重矩阵过于复杂，可能造成模式之间的相互干扰和混淆。此外，网络的稳定性也会随模式数量的增多而降低，表现为原本能够成功回忆的模式在加入新的模式后无法准确回忆出来。

鉴于以上优缺点，Hopfield网络在特定场合如图像恢复、优化问题等有限规模的模式记忆和优化任务中仍然有着实用价值，但在处理大规模、复杂或噪声严重的数据时，可能需要结合其他更先进的神经网络模型或算法来改进其性能。