当前位置：首页 > news >正文

从错误思路到滑动窗口：力扣2962“包含至少K个最大值”的子数组计数问题---left的解读

news 2025/5/1 8:08:20

在写每日力扣时遇到的题，乍一看1700的题好像可以直出，结果是思路假了，还是菜了。附上题目链接

一、错误的初始思路及其问题

在初次尝试解决这个问题时，我第一个直观的想法是先存下所有最大值出现的位置，直接类似滑动窗口但只记录窗口前半截。（很显然这就是病因，之后果然是因为漏了后半截窗口位置导致思路不全，如果你已经一言顶真，那可以直接查看滑动窗口和第二部分我的卡点ans+=left）

我的初始思路是这样的（代码如下）：先将所有 max_ 出现的位置存储在一个向量 map 中。map[i] 表示第 i+1 个最大值在原数组中的索引。然后直接将map数组中每个小于等于lenmap-k的位置加给cnt，cnt是最终返回的数，lenmap-k是保证子数组内max_个数大于等于k个。看着很合理对吧，样例1、2也都通过了

class Solution {
public:long long countSubarrays(vector<int>& nums, int k) {int max_ = 0;for (int x : nums) {max_ = max(max_, x);}vector<int> map; // 存储最大值的位置for (int i = 0; i < nums.size(); ++i) {if (nums[i] == max_) {map.emplace_back(i);}}int lenmap = map.size();if(lenmap < k)return 0;long long cnt = 0;// 错误尝试：基于最大值位置进行计数for (int i = 0; i <= lenmap - k; ++i) {// 这里的逻辑是简陋暴力的！cnt += map[i] + 1;}return cnt;}
};

但直接在63号测试用例附近被gank了悲(；′⌒`)

那么，这个思路为什么是错误的呢？

原因：忽略了子数组的结束边界，简单地以为每个子数组都是以max_为尾元素： map[i] 是第 i+1 个最大值在原数组中的索引。map[i] + 1 仅仅代表以这个最大值位置为结束的所有子数组的数量（从索引 0 到 map[i]，也是窗口的0->left）。这没有错，所以样例也能过去。但是这只是因为样例1里只需要考虑到 0 -> left 也足够了，而当出现 [ 1, 82, 1 ,82 ,2 ,82 ] 时：

二、差个2漏在哪了呢？

如果看过题解就会发现题解的滑动窗口的思路好像跟我们差不多，但是实际打输出追踪ans就会发现端倪：

在第一个符合k的窗口转向第二个时，竟然也加了个2

经过观察发现这个2是left 累计下来的，题解的过程是这样：

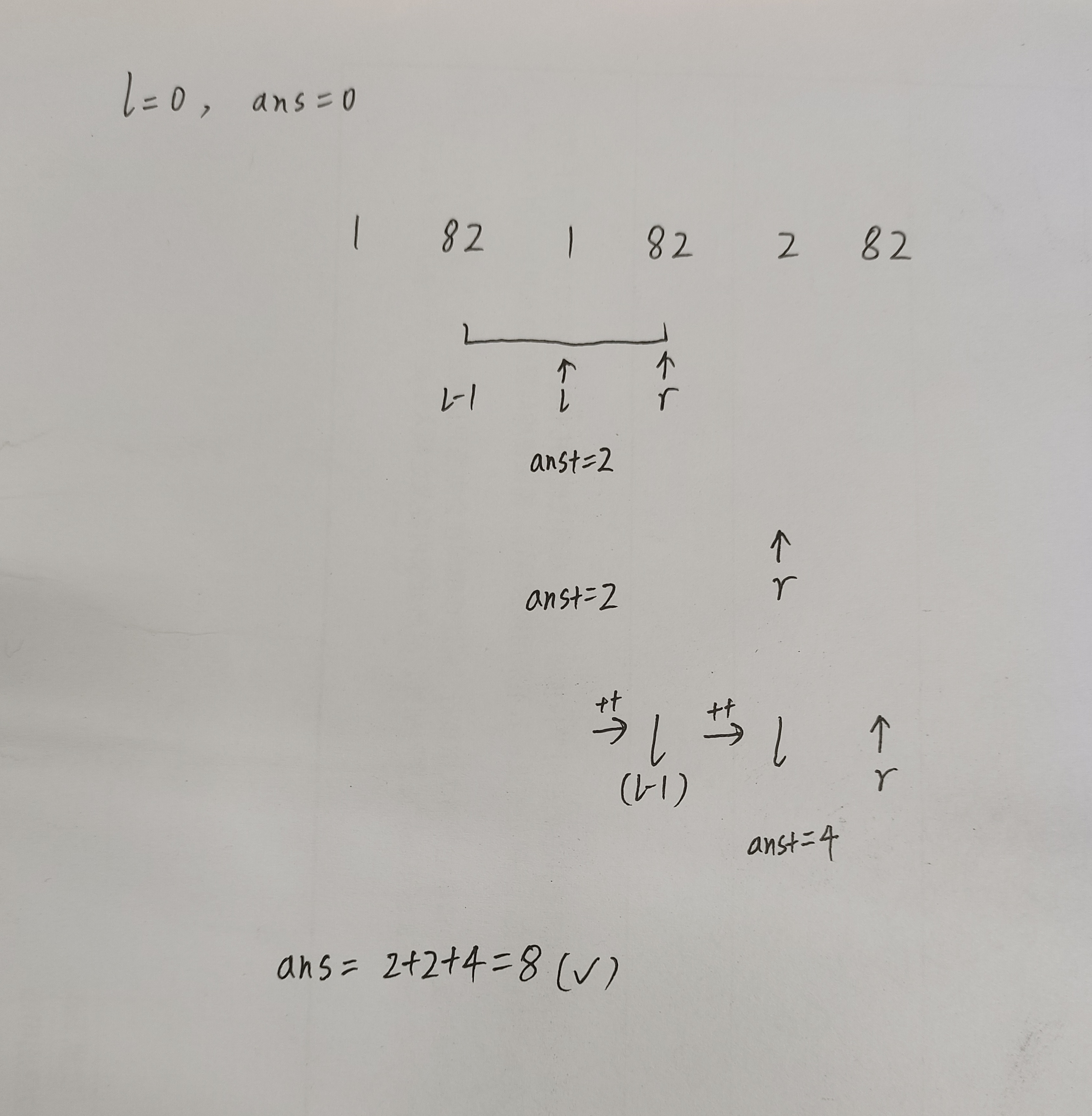
而我们之前的代码遗漏的2是：

所以可以发现这个left至关重要

left定义是

int left= 0;    //之前已知的从left-1到之前r的子数组数量

而

ans += left; //将本次更新后的left-1到现在的r的子数组数量加上

第二部分：正确的滑动窗口思路

解决包含“至少 K 个”元素子数组计数问题的常用且高效的方法是滑动窗口（Sliding Window）。滑动窗口的核心思想是用两个指针 left 和 right 维护一个动态的子数组窗口 nums[left...right]，并在遍历数组的过程中调整窗口大小，使其满足特定条件。

对于本题，我们的目标是统计包含至少 k 个最大值的子数组数量。我们可以让 right 指针从数组开头向右遍历，表示当前考虑的子数组的结束位置。同时，用 left 指针表示子数组的起始位置。我们需要维护一个窗口 [left...right]，并确保它包含至少 k 个最大值。

具体步骤如下：

首先，找到数组中的最大值 max_。
初始化 left = 0，cnt_mx = 0 (当前窗口中最大值的数量)，以及 ans = 0 (最终结果)。
使用 right 指针遍历整个数组 (可以由外层循环的索引 i 表示)。
当 right 指针移动到新位置 i 时，如果 nums[i] 是最大值 max_，则将 cnt_mx 加一。
现在，我们考虑以当前的 right (或 i) 为结束位置的所有子数组。我们希望找到所有合法的起始位置 left，使得子数组 nums[left...i] 包含至少 k 个最大值。
关键步骤： 当当前窗口 nums[left...i] 包含至少 k 个最大值 (cnt_mx >= k) 时，这意味着以 i 为结束，以 left 为起始的子数组是满足条件的。而且，由于 right 是固定的，如果 [left...i] 满足条件，那么任何以比 left 更靠左的位置为起始的子数组 [left' ... i] (其中 left' < left) 也必然包含至少 k 个最大值。
为了找到所有以 i 为结束的满足条件的子数组的起始位置数量，我们使用一个 while 循环来移动 left 指针。当 cnt_mx >= k 时，我们将 left 向右移动。如果移动 left 后，nums[left] 是最大值，则 cnt_mx 减一。这个 while 循环会一直执行，直到窗口 nums[left...i] 中的最大值数量 cnt_mx 小于 k。
在 while 循环结束后，当前的 left 指针指向的位置是满足以下条件的第一个位置：以该位置为起始，以当前的 i 为结束的子数组 nums[left...i] 包含的最大值数量小于 k。
这意味着，所有从索引 0 到 left - 1 之间的位置，都可以作为以当前的 i 为结束位置，并且包含至少 k 个最大值的子数组的起始位置。这样的起始位置共有 left 个。
因此，我们将当前的 left 值累加到总数 ans 中。ans += left。
重复步骤 3-10，直到 right 指针遍历完整个数组。

以下是使用滑动窗口解决此问题的 C++ 代码（考虑至少 k 个最大值的情况）：


class Solution {
public:long long countSubarrays(vector<int>& nums, int k) {int max_ = 0;for (int x : nums) {max_ = max(max_, x);}long long ans = 0;int n = nums.size();int cnt_max = 0; // 窗口 [left...right] 中最大值的数量int left = 0;    // 窗口的左边界  //之前已知的从left-1到之前r的子数组数量// right 指针由外层循环的 i 表示for (int i = 0; i < n; ++i) {// 将 nums[i] (当前 right 指向的元素) 加入窗口if (nums[i] == max_) {cnt_max++;}// 当窗口 [left...i] 包含至少 k 个最大值时，收缩左边界// 这里的重点在于找到以 i 结束的合法起始位置数量while (cnt_max >= k) {// 移动 left 指针，直到窗口不再包含至少 k 个最大值if (nums[left] == max_) {cnt_max--;}left++; // 收缩窗口左边界}// 此时 while 循环结束后，left 是第一个不满足条件的起始位置// 从 0 到 left-1 的所有位置都可以作为起始，与 i 组成满足条件的子数组// 这样的起始位置数量为 leftans += left;        //将本次更新后的left-1到现在的r的子数组数量加上}return ans;}
};

通过滑动窗口，我们能够在 O(n) 的时间复杂度内高效地解决这个问题。尽管代码看起来简洁，但其中 while 循环结束后 ans += left 这一步的理解至关重要，它巧妙地累加了所有以当前 right 为结束的合法子数组数量。也考虑了我之前遗漏右边界的问题

总结与反思

避免陷入表面模式： 我的第一个错误思路就是只看到了“最大值的位置”这个表面特征，并想当然地基于这些点进行计数，而没有深入思考子数组作为一个“区间”的属性以及如何系统地遍历和统计所有可能的区间。~~这提醒我，遇到问题时，不要急于套用看似相关的模式，而要花时间理解问题的本质。~~而是不要轻敌，要先用猪脑过一遍样例，在有思路之后，思考可能的样例卡点，但尽量控制时间。
ans += left 的突破性理解： 最初，ans += left 这一步让我非常困惑，感觉它只是简单地累加了 left 的值，而没有直接对应子数组的数量。通过一步步的推导和思考（正如第二部分详细讲解的），我才意识到 left 在 while 循环结束后，其值恰好代表了以当前 right 为结束、且满足条件的子数组的起始位置数量。这一突破性的理解是掌握滑动窗口计数精髓的关键。它告诉我，算法中的每一步都有其深刻的含义，不能想当然地跳过。
实践出真知： 理论知识是基础，但只有亲手实践、 Debug、并结合具体例子进行推导，才能真正将知识转化为能力。正是在反复尝试理解 ans += left 的过程中，我才彻底掌握了它。