深入理解 X25519 与 Ed25519：密钥交换与签名验签全流程解析

在现代密码学体系中，椭圆曲线密码（ECC）凭借 “短密钥长度 + 高安全性” 的优势，成为 TLS、SSH、区块链等场景的核心技术。其中，X25519 与 Ed25519 是基于 Curve25519 椭圆曲线的两大核心算法 ——X25519 专注于密钥交换，Ed25519 专注于数字签名。本文将从基础概念出发，逐步拆解两者的核心流程，帮助读者建立从理论到实践的完整认知。

一、前置概念：厘清关键术语与基础理论

在深入流程前，需先明确两个易混淆的概念，同时掌握 ECC 的核心原理：

1.1 X25519 与 Ed25519 的区别

很多初学者会将两者混淆，实则定位完全不同：

• X25519：基于 Curve25519 的密钥交换算法（ECDH 的优化实现），作用是让通信双方在不安全信道中协商出共享密钥（用于后续数据加密）；

• Ed25519：基于 Curve25519 的数字签名算法（ECDSA 的优化实现），作用是验证消息完整性、身份真实性（即 “签名验签” 流程）。

简言之：X25519 解决 “密钥怎么安全协商”，Ed25519 解决 “消息怎么安全验证”。

1.2 椭圆曲线密码（ECC）核心原理

ECC 的安全性基于 “椭圆曲线离散对数问题”（ECDLP），其核心是点运算。需理解三个关键概念：

1. 椭圆曲线方程：Curve25519 采用的方程为 \( y^2 = x^3 + 486662x^2 + x \)（定义在有限域 \( GF(2^{255}-19) \) 上，即所有运算结果需对 \( 2^{255}-19 \) 取模）；
2. 基点 G：Curve25519 定义的固定点 \( G = (9, ...) \)（具体坐标可通过标准文档查询），是密钥生成的 “基准”；
3. 点乘运算：若私钥为 \( k \)（一个 256 位随机数），公钥则为 \( K = k \times G \)（即 “将 G 自身相加 k 次”，ECC 的核心运算，逆向求解 k（离散对数）在计算上不可行）。

二、X25519：密钥交换流程详解

X25519 是 ECDH（椭圆曲线 Diffie-Hellman）的优化版本，解决了传统 ECDH 的侧信道攻击风险和兼容性问题。其核心目标是让通信双方（如 Alice 和 Bob）在公开信道中协商出相同的共享密钥，且第三方无法破解。

2.1 流程总览

X25519 密钥交换分为 3 步：密钥生成→公钥交换→共享密钥计算，流程如下图所示：

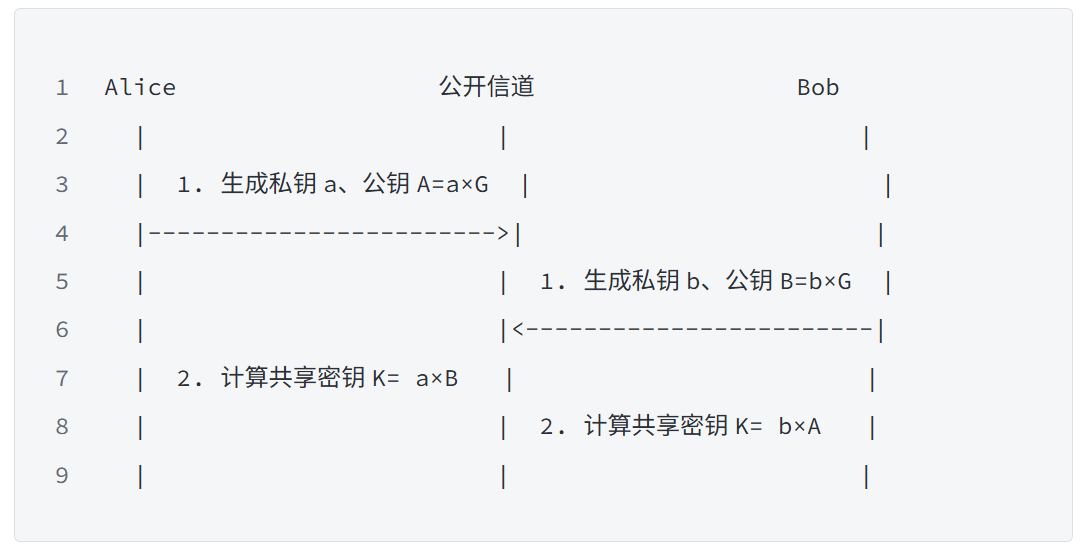
2.2 关键步骤拆解

步骤 1：私钥与公钥生成

• 私钥生成：

从随机数生成器中获取 32 字节（256 位）的随机数，需满足 “清除最高位”（确保在 Curve25519 的安全子群内），最终得到私钥（如 Alice 的私钥a，Bob 的私钥b）。

• 公钥生成：

通过点乘运算计算公钥：公钥 = 私钥 × 基点G（如 Alice 的公钥A = a×G，Bob 的公钥B = b×G）。公钥是椭圆曲线上的一个点，用 32 字节表示（仅存储 x 坐标，y 坐标可通过曲线方程推导）。

步骤 2：公钥交换

Alice 将公钥A通过公开信道发送给 Bob，Bob 将公钥B发送给 Alice。此时第三方（如 Eve）可获取A和B，但无法从公钥反推私钥（ECDLP 问题）。

步骤 3：共享密钥计算

• Alice 收到 Bob 的公钥B后，用自己的私钥a计算：K_Alice = a × B；

• Bob 收到 Alice 的公钥A后，用自己的私钥b计算：K_Bob = b × A；

• 核心等式：根据 ECC 点乘的交换律，a×B = a×(b×G) = b×(a×G) = b×A，因此K_Alice = K_Bob = K（即双方得到相同的 32 字节共享密钥）。

步骤 4：共享密钥派生（可选但必需）

直接得到的 32 字节共享密钥K通常不直接用于加密，需通过密钥派生函数（KDF） 处理（如 HKDF-SHA256），生成最终的会话密钥（用于 AES 等对称加密算法）。KDF 的作用是：

1. 消除共享密钥中的 “偏置”（确保密钥随机性）；
2. 生成符合后续加密算法要求的密钥长度；
3. 绑定上下文信息（如协议版本、双方身份），防止 “密钥重用攻击”。

三、Ed25519：签名与验签流程详解

Ed25519 是基于 Curve25519 的数字签名算法，相比传统 ECDSA，具有 “无随机数安全漏洞”“签名速度快”“签名尺寸小”（64 字节）的优势，广泛用于代码签名、区块链交易、API 身份验证等场景。

其核心逻辑是：签名者用私钥对消息生成签名，验证者用公钥验证签名是否合法（即消息未被篡改、签名确为对应私钥生成）。

3.1 流程总览

Ed25519 流程分为 3 步：密钥生成→签名生成→签名验证，流程如下图所示：

3.2 关键步骤拆解

步骤 1：密钥生成（与 X25519 差异显著）

Ed25519 的密钥生成引入了哈希运算，增强安全性：

1. 私钥生成：

生成 32 字节随机数seed，对seed做 SHA-512 哈希，取前 32 字节作为 “核心私钥”sk_core，后 32 字节用于后续签名计算（避免随机数漏洞）；

    2.公钥生成：

用sk_core与基点 G 做带符号的点乘（适配 Edwards 曲线格式），得到公钥pk（32 字节，直接存储曲线上点的坐标压缩形式）。

注：Ed25519 私钥通常包含seed（32 字节），可通过seed重新推导公钥；而 X25519 私钥就是 32 字节随机数，无法从私钥反推公钥（需重新计算点乘）。

步骤 2：签名生成（核心流程）

假设 Alice 要对消息M生成签名，步骤如下：

1.计算哈希值 r：

用 SHA-512 哈希算法，对 “Ed25519 私钥后 32 字节 + 消息 M” 做哈希，取哈希结果的低 256 位作为r（临时私钥，每次签名不同）；

2.计算临时公钥 R：

用r与基点 G 做带符号的点乘，得到临时公钥R（32 字节，曲线上的点）；

3.计算挑战值 h：

用 SHA-512 哈希算法，对 “临时公钥 R + 公钥 pk + 消息 M” 做哈希，取哈希结果的低 256 位作为h（挑战值，绑定 R、pk、M）；

4.计算签名 S：

按公式 S = (r + h × sk_core) mod (2^252 + 27742317777372353535851937790883648493) 计算S（256 位，签名的核心部分）。

最终签名Sig由 “临时公钥 R（32 字节） + 签名 S（32 字节）” 组成，共 64 字节。

步骤 3：签名验证（核心流程）

Bob 收到消息M、Alice 的公钥pk和签名Sig（R + S）后，验证步骤如下：

1.格式校验：

检查pk（32 字节）、R（32 字节）、S（32 字节）的长度是否合法，且R是否在 Curve25519 的安全子群内（避免 “无效点攻击”）；

2.重新计算挑战值 h：

用与签名生成相同的哈希算法，对 “R + pk + M” 做哈希，取低 256 位得到h（需与 Alice 计算的h完全一致，否则签名无效）；

3.验证椭圆曲线等式：

核心验证逻辑基于 ECC 的点运算等式：

S × G = R + h × pk

具体计算步骤：

• 左侧：计算S × G（带符号点乘，得到曲线上的点 P1）；
• 右侧：计算h × pk（带符号点乘，得到点 P2），再与R做点加运算（得到点 P3）；
• 对比：若P1 == P3，则签名合法；否则签名无效（消息被篡改或签名伪造）。

原理：若签名为 Alice 生成，根据签名生成时的公式S = r + h×sk_core，两边乘 G 可得S×G = r×G + h×sk_core×G = R + h×pk，等式必然成立；若签名伪造，攻击者无法构造满足该等式的 R 和 S。

四、深入细节：安全性与实践注意事项

4.1 核心安全性设计

1.抗侧信道攻击：

X25519 和 Ed25519 的点乘运算均采用 “固定窗口法”，避免因运算步骤差异泄露私钥（传统 ECC 易因分支预测、缓存时序泄露信息）；

2.无随机数依赖：

Ed25519 的签名生成中，r由 “私钥片段 + 消息” 哈希生成（确定性签名），无需额外随机数，避免了 ECDSA 因随机数泄露导致的私钥破解风险；

3.短密钥高安全：

256 位的 X25519/Ed25519 密钥安全性等同于 3072 位的 RSA 密钥，但密钥长度仅为 RSA 的 1/10，适合资源受限场景（如 IoT 设备）。

4.2 实践中的常见问题

1.公钥验证不可少：

接收方在使用 X25519 公钥计算共享密钥前，需验证公钥是否在 Curve25519 的安全子群内（否则可能遭遇 “小 subgroup 攻击”）；

2.签名消息需完整：

Ed25519 签名绑定 “消息全量哈希”，若消息被截断或修改，哪怕 1 字节，h值也会完全不同，验证必然失败；

3.密钥存储需安全：

X25519 私钥和 Ed25519 的seed均为敏感信息，需存储在安全硬件（如 TPM、SE）中，避免明文存储导致泄露。

五、应用场景：从理论到实践

X25519 与 Ed25519 已成为行业标准，典型应用场景包括：

5.1 TLS 1.3：

客户端与服务器通过 X25519 协商预主密钥（ECDHE 握手），证书链中的签名采用 Ed25519（替代传统 RSA 签名，提升握手速度）；

5.2 SSH 协议：

服务器通过 Ed25519 签名认证身份，用户通过 X25519 与服务器协商会话密钥（替代 DH 算法，减少带宽消耗）；

5.3 区块链与加密货币：

比特币、以太坊等项目支持 Ed25519 签名（用于交易签名，64 字节签名尺寸远小于 ECDSA 的 72 字节）；

5.4 端到端加密（E2EE）：

Signal、WhatsApp 等即时通讯软件用 X25519 协商会话密钥，用 Ed25519 验证用户身份（确保消息不被中间人篡改）。

六、总结

X25519 与 Ed25519 是 Curve25519 椭圆曲线的 “双子星” 算法：

• X25519：通过 “私钥→公钥→共享密钥” 的流程，解决 “密钥安全协商” 问题，核心是 ECC 点乘的交换律；

• Ed25519：通过 “哈希绑定 + 点运算验证” 的流程，解决 “消息身份验证” 问题，核心是确定性签名与椭圆曲线等式验证。

两者共同构成了现代密码学的基础组件，其 “高效、安全、简洁” 的特性，使其在各类安全场景中逐步替代传统 RSA 和 ECDSA。理解其核心流程，不仅能帮助开发者正确使用加密库（如openHiTLS、OpenSSL），更能应对实际场景中的安全挑战（如密钥管理、攻击防护）。