数据结构面试重点

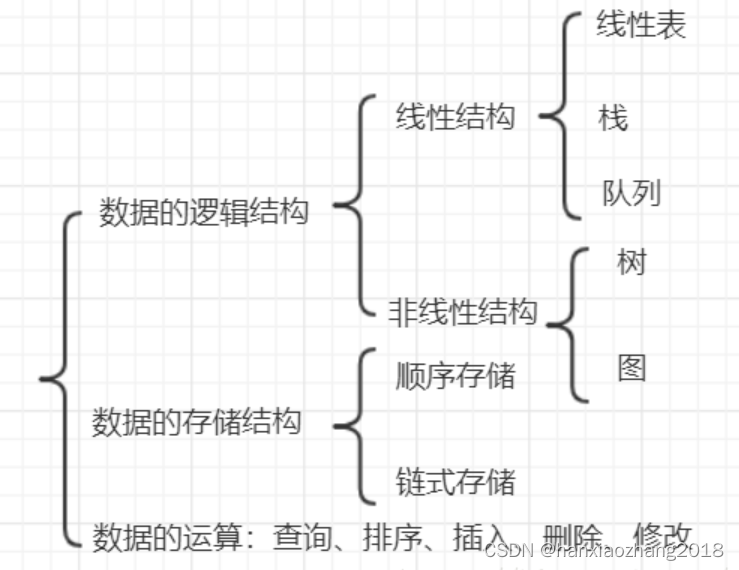
1. 数据结构的三个方面：（@&@）

数据的逻辑结构、数据的存储结构、运算规则

2. 线性表：

概念：

由n（n>=0）个类型相同的数据元素（a0，a1，…an-1）组成的有限序列。

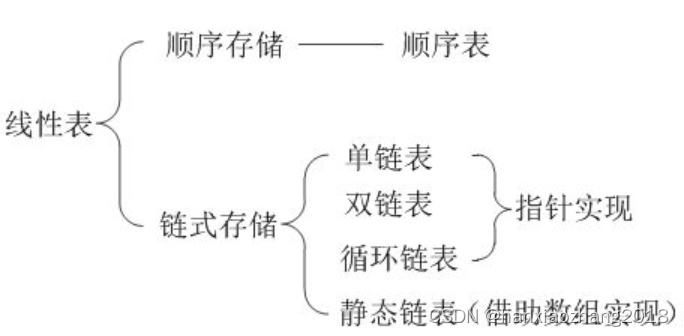
分类：

顺序存储（顺序表）、链式存储（单链表、双链表、循环链表、静态链表）

特点：

• 顺序表：查询的时间复杂度是O(1)（根据索引查找），插入或删除的时间复杂度是O(n)。
• 链表：查询的时间复杂度是O(n)，插入或删除的时间复杂度是O(n)。

3. 单链表：

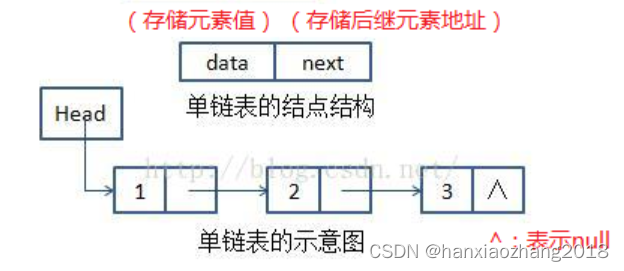
概念：

一种链式存取的数据结构，每个节点由元素 + 指针组成。

操作（重点背下，翻转）：

• 插入：

# 头节点为空插入：
head = new Node(10,null);
# 头节点插入：
Node node = new Node(10,null);
head.next=node;
# 中间节点插入(p节点)：
Node node = new Node(10,p.next);
node.next=p;

• 删除：

# 头结点删除：
head = null;
# 中间节点删除（删除p节点的后继节点）：
p.next =p.next.next;

• 循环：

while(head != null){System.out.println(head.data);head = head.next;
}

• 翻转：总是忘记
  • 思路：声明一个前继节点指针，从head节点开始，循环把后继节点指向前继节点。
  • 具体步骤：看代码注释

public Node reverse(Node head){// 声明当前节点的继节点指针 当前节点的后继节点指针 当前节点Node pre = null,next = null,cur=head; while (cur != null) {  // 循环条件，当前节点不为空next = cur.next;  // 获取当前节点的后继节点，赋值给nextcur.next = pre;  // 将当前节点的后继节点，指向前继节点pre = cur;  // pre赋值成cur，即下一次循环节点的前继节点是当前节点。cur = next; // cur赋值成next，即移动到循环的下一个节点}return pre;
}

单向链表的第N个节点前插入一个节点：

思路：先将M结点插入到N结点后，然后将N结点存储的值和M结点存储的值互换

4. 双链表：

概念：

一种链式存取的数据结构，每个结点有两个地址域的链表。

重要关系（p节点为例）：

p = p.prev.next = p.next.prev

操作：

• 插入：

# 头结点为空插入：
head = new Node(10,null,null);
# p节点之前插入：
Node node = new Node(10,p.prev,p);
p.prev.next = node;
p.prev = node;
# p节点之后插入：
Node node = new Node(10,p,p.next);
if(p.next != null){p.next.prev = node;
}
p.next = node;

• 删除：

# 头结点删除：
head = null;
# 删除（p节点）：
p.prev.next = p.next;
if(p.next != null){p.next.prev =p.prev;
}

• 翻转：
  • 思路，从head节点开始，循环将两个指针方向翻转。

public DoubleNode reverse(DoubleNode head) {// 声明前继节点 后继节点 当前节点DoubleNode pre = null,next = null,cur=head;while (cur != null) {  // 循环条件：当前节点不为空next = cur.next; // 获取当前节点的后继节点，赋值给next// 当前节点的两个指针方向翻转cur.next = pre;  cur.pre = next; pre = cur; // pre赋值成cur，即下一次循环节点的前继节点是当前节点cur = next; // cur赋值成next，即移动到循环的下一个节点}return pre;
}

5. 二叉树：

概念：

二叉树是每个结点最多有两个子树的树结构。

性质：

• 性质1：二叉树第 i 层上的结点数目最多为 2{i-1} (i≥1)。
• 性质2：深度为 k 的二叉树至多（完满二叉树）有2{k}-1个结点(k≥1)。
• 性质3：包含 n 个结点的二叉树的高度至少为[log2 n]+1。注：[ ]表示向下取整
• 性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。
• Tips：结点的度：结点所拥有的子树个数。

三种访问方式：***

• 先序遍历：根节点->左子树->右子树
• 中序遍历：左子树->根节点->右子树
• 后序遍历：左子树->右子树->根节点
• 实现：使用递归序

public static void tree(Node head) {if (head == null) {return;}// 先序开启打印： System.out.print(head.value + " ");tree(head.left);// 中序开启打印： System.out.print(head.value + " ");tree(head.right);// 后序开启打印： System.out.print(head.value + " ");
}

按层遍历：Pass

• 思路：
  • 1. 首先把头结点放入队列。
  • 2. 循环判断队列是否为空。
  • 3. 不为空，打印队列弹出节点，并且将弹出节点的左右孩子节点存入队列。
  • 4. 循环执行 2 3。

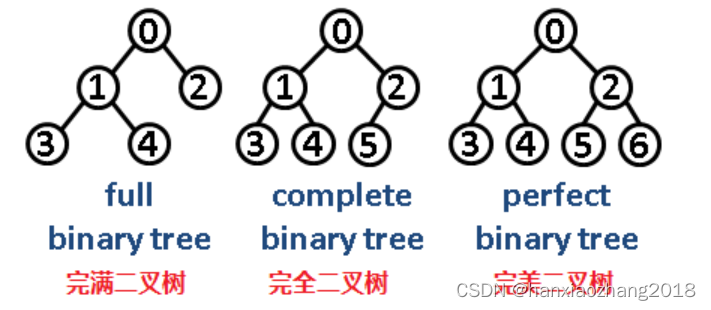
完满二叉树、完全二叉树、完美二叉树:

• 完满二叉树：除了叶子结点之外的每一个结点都有两个孩子结点。
• 完全二叉树（CBT）：
  • 除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐。
  • 是不是完全二叉树的代码：com.hanxiaozhang.tree.binarytreerecursion.IsCBT
• 完美二叉树：
  • 除了叶子结点之外的每一个结点都有两个孩子，每一层(当然包含最后一层)都被完全填充。
  • 是不是完美二叉树的实现思路：递归求出树的深度和节点个数，判断(1

6. 二叉排序树（二叉搜索数）：

概念：

二叉排序树（BST），又称二叉查找树。它可以实现数据的快速查找。二叉排序树的中序遍历结果是有序。

性质：

• 性质1：若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 性质2：若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 性质3：左、右子树也分别为二叉排序树；
• 性质4：没有键值相等的节点。

判断树是否是BST？

• 思路1：BST在中序遍历时是有序的，具体：通过递归序把中序结果存入数组，然后判断数组是否有序。

7. 平衡二叉树（AVL树）：

概念：

它是特殊的二叉排序树（平衡二叉树基于二叉查找树）。它特点：左子树和右子树都是平衡二叉树。左右两棵子树的高度之差不超过1。

好处：

避免二叉查找树退化成链表的问题，把插入、查找、删除的时间复杂度最好情况和最坏情况都维持在O(logN)。

应用场景：

AVL树适合用于插入删除次数比较少，但查找多的情况。插入删除会导致很多的旋转，旋转非常耗时。

常用实现方法：

红黑树、AVL、替罪羊树、Treap、伸展树等

8. 红黑树：

概念：

一种含有红黑节点，并能自平衡的二叉查找树。

性质：

• 性质1：每个节点要么是黑色，要么是红色。
• 性质2：根节点是黑色。
• 性质3：每个叶子节点（NIL）是黑色。
• 性质4：每个红色节点的两个子结点一定都是黑色。
• 性质5：任意节点到每个叶子节点的路径都包含数量相同的黑节点。

其他（自平衡原理等）：

操作：左旋、右旋、变色，见《红黑树2019-12-09》

应用场景：

红黑树是一种不是非常严格的平衡二叉树，所以它的平均查找，增添删除效率都还不错。例如，HashMap中用到了红黑树。

9. B树（平衡多路查找树）：

概念：

B树属于多叉树，它是平衡多路查找树。 下图使用三叉树来举例：

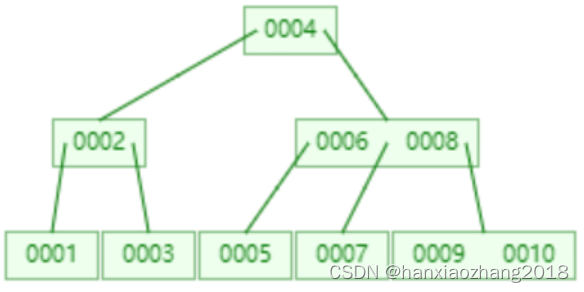
满足的条件：

• 树中的每个节点多拥有m个子节点，且m>=2，空树除外。（Tips：m阶代表一个树节点有多少个查找路径。m阶=m路，当m=2则是二叉树，m=3则是三叉树）
• 除根节点外每个节点的关键字数量大于等于ceil(m/2)-1个，小于等于m-1个，非根节点关键字数必须>=2。（Tips：ceil()是个朝正无穷方向取整的函数，如ceil(1.1)结果为2)
• 所有叶子节点均在同一层，叶子节点除了包含了关键字和关键字记录的指针外，也有指向其子节点的指针，只不过其指针地址都为null。
• 如果一个非叶节点有N个子节点，则该节点的关键字数等于 N-1。
• 所有节点关键字是按递增次序排列，并遵循左小右大原则。

应用场景：

构造一个多阶的B类树，在尽量多的在结点上存储相关的信息，来保证层数尽量的少，方面可以更快的找到信息，磁盘的I/O操作也少一些。

10. B+树（B数的变种树）：

概念：

B+树是B树的变种树，有n棵子树的节点中含有n个关键字，每个关键字都不保存数据，只是用来索引，数据都保存在叶子节点中。相对于B树来说，B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。下图使用三叉树来举例：

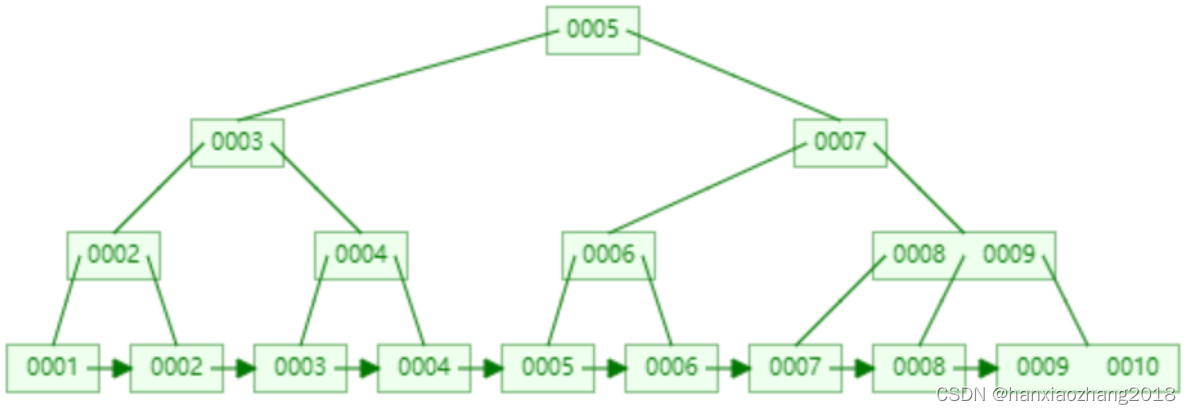
B+树与B树的区别：***

• B+树的叶子节点保存了父节点的所有关键字和关键字记录的指针，每个叶子节点的关键字从小到大链接。
• B+树的非叶子节点只进行数据索引，不会存实际的关键字记录的指针，所有数据地址必须要到叶子节点才能获取到，所以，每次数据查询的次数都一样。
• B+树的根节点关键字数量与其子节点个数相等。

特点： **

• 在B树的基础上，每个节点可以存储更多数量的关键字，树的层级就会更少，所以查询数据更快。
• 所有关键字的指针都存在叶子节点，每次查找的次数都相同，所以查询速度稳定。

应用场景：

磁盘文件组织数据索引和数据库索引。

11. Trie树（字典树\前缀树） ：Pass

概念：

它是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

在图示中，键标注在节点中，值标注在节点之下。每一个完整的英文单词对应一个特定的整数。Trie可以看作是一个确定有限状态自动机，尽管边上的符号一般是隐含在分支的顺序中的。

键不需要被显式地保存在节点中。图示中标注出完整的单词，只是为了演示Trie的原理。

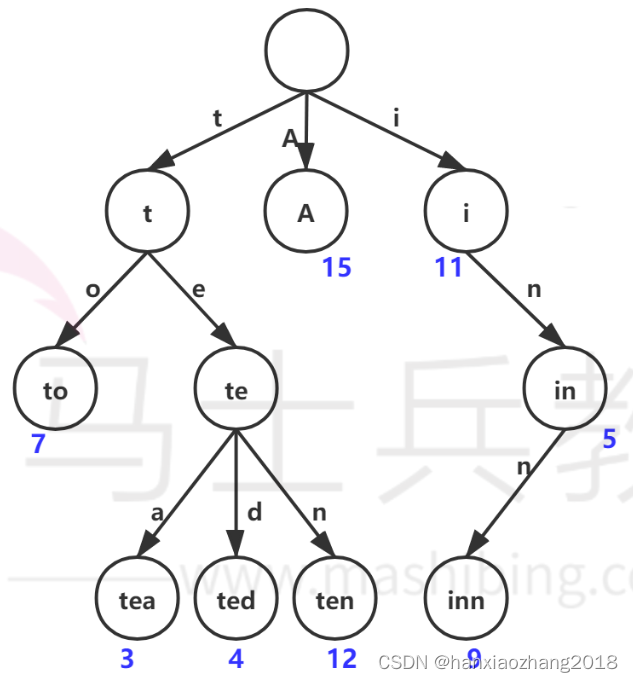
优点：利用字符串的公共前缀来节约存储空间，大限度地减少无谓的字符串比较，查询效率比哈希表高。

缺点：Trie树的内存消耗非常大。

性质：

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
• 每个节点的所有子节点包含的字符都不相同。

典型应用：

用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

实现：

见com.hanxiaozhang.tree.PrefixTree1; 见com.hanxiaozhang.tree.PrefixTree2;

12. 栈和队列的结构：

数组实现栈结构：

思路：维护一个index指针，size大小和capacity容量。push时，index++。pop时，返回index位置的元素，并且index--。size==0时，栈为空。size==capacity时，栈满了。

见 com.hanxiaozhang.stackandqueue.StackArray

数组手写循环队列：

思路：维护两个指针：pushIndex和pollIndex，size大小和capacity容量。如何实现循环，判断下一个指针时用 nextIndex = index < capacity - 1 ? index + 1 : 0

见 com.hanxiaozhang.stackandqueue.QueueArray

使用链表手写栈和队列：（复杂 pass ）

见 com.hanxiaozhang.stackandqueue.StackQueueLinked

13. 堆：

概念：

堆结构就是用数组实现的完全二叉树结构。在完全二叉树中，如果每棵子树的最大值都在顶部就是大根堆，反之小跟堆。堆结构最重要的两个操作：heapInsert（插入堆）与heapify（堆化，将整个数组构建成一个堆）。优先级队列结构，就是堆结构。

堆与数组之间的转换：***

• 使用从0开始的数组表示堆（这个背下来）：（@&@）

i节点 ==> 左节点 2*i+1 、右节点 2*i+2 、父节点 (i-1)/2

• 使用从1开始的数组表示堆（数组0索引位置不使用）：（这个先pass）

i节点==> 左节点 2*i （i << 1）、右节点 2*i+1 (i <<1 | 1) 、父节点 i/2 (i >> 1)

实现：（heapify pass ）

见com.hanxiaozhang.heap.MaxHeap