数据结构之二叉树（1）

树是另一种形式的海。
在数据结构中，也有树这个东西。

1.树的概念与结构

在前面的数据机构中，我们学习的都是线性表。而树是一种非线性的数据结构，它是由n个有限结点组成的一个具有层次关系的集合。顾名思义，它看起来像一颗倒过来的树。也就是根朝上，而叶朝下。

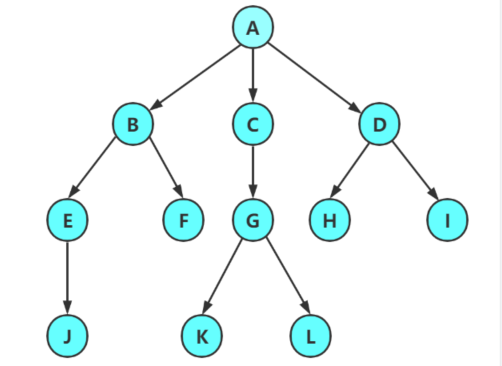
每棵树都有一个根结点。
除根结点外，其余结点被分成多个互不相交的集合。每个集合又是一颗子树。每颗子树都有一个根结点，可以有0个或多个后继。所以树是递归定义的。
树的一些特性：

• 子树是不相交的。
• 除了根结点，每个结点有且仅有一个父结点。
• 一个N个结点的树有N-1条边。

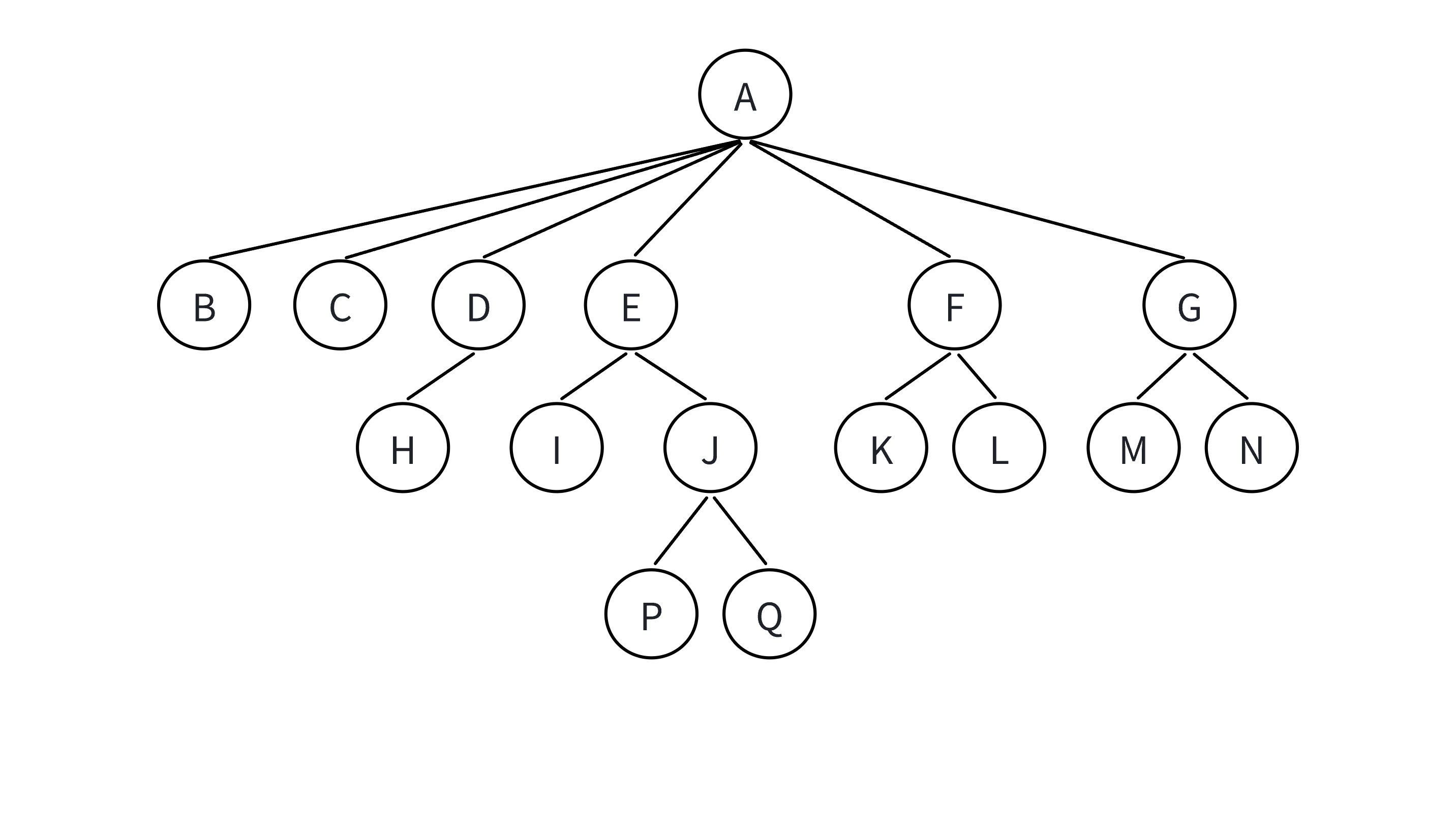
2.树的相关术语

3.树的分类

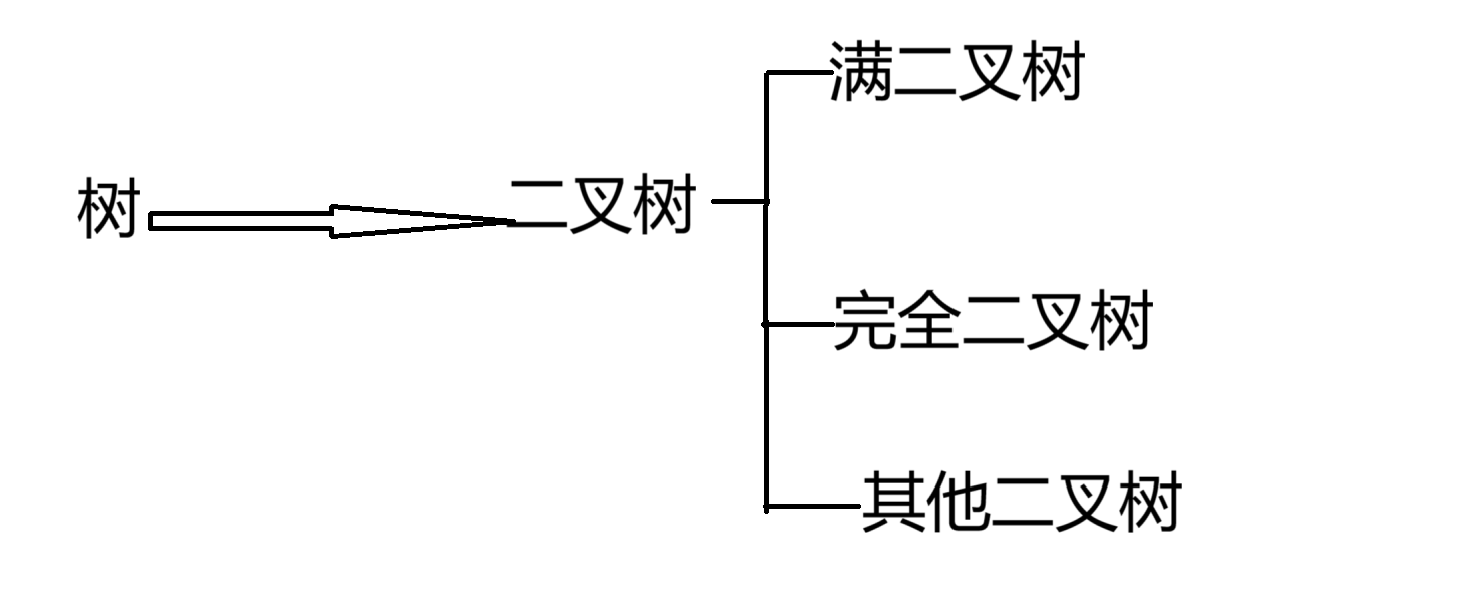
在树形结构中，我们最常⽤的就是⼆叉树，⼀棵⼆叉树是结点的⼀个有限集合，该集合由⼀个根结点加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。
二叉树具有以下特性：

• ⼆叉树不存在度⼤于 2 的结点
• ⼆叉树的⼦树有左右之分，次序不能颠倒，因此⼆叉树是有序树
  
  对于任意的⼆叉树都是由以下⼏种情况复合⽽成的：
  1.空树
  2.只有根结点
  3.只有左子树或右子树
  4.左右子树均存在

3.1满二叉树

⼀个⼆叉树，如果每⼀个层的结点数都达到最⼤值，则这个⼆叉树就是满⼆叉树。

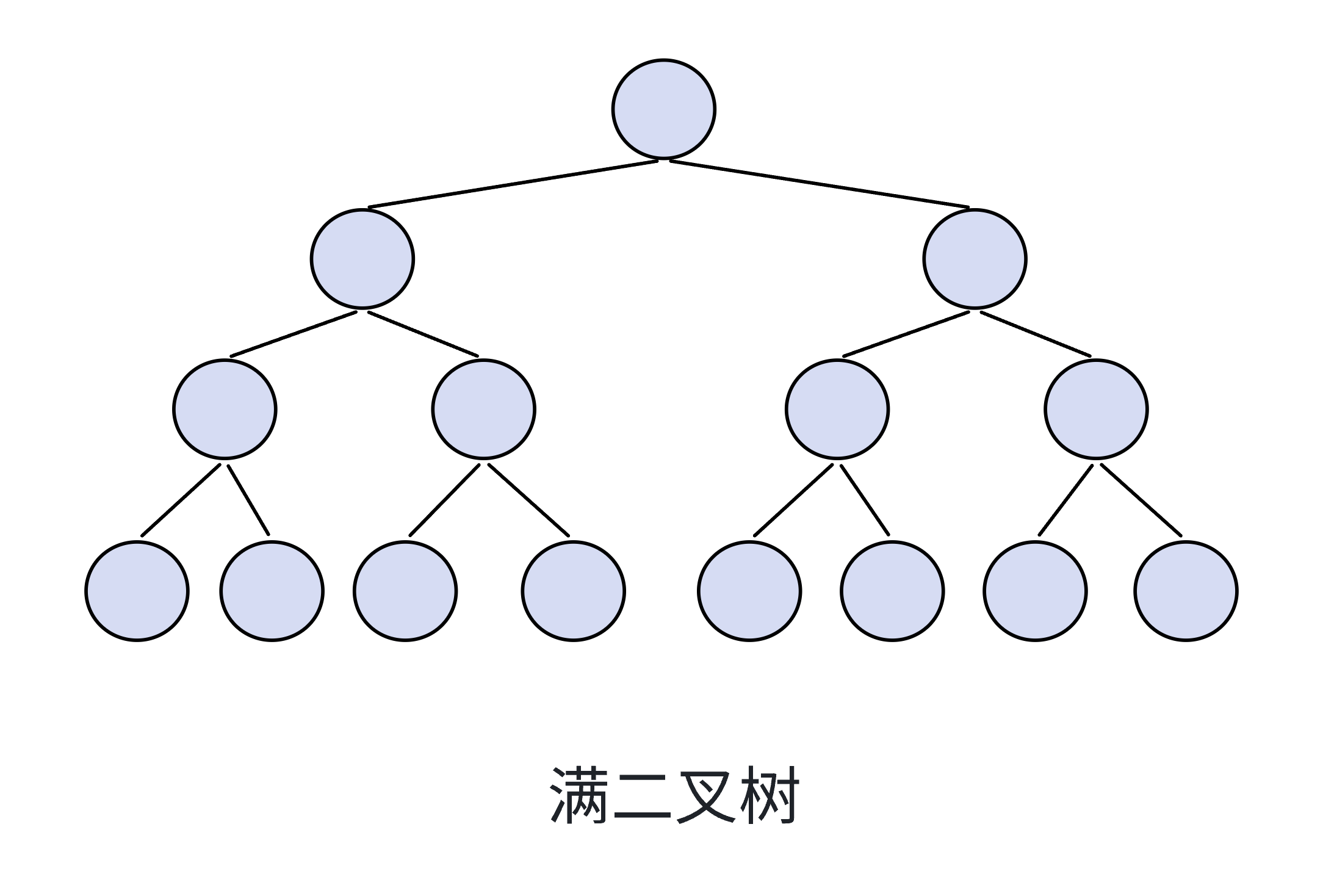
假设二叉树的高度为k，则第k层节点个数为2^(k-1)
则满二叉树总的结点个数：2^0 + 2^1 +2^3 +… +2^(k-1)= 2^k - 1(等比数列求和公式)
若规定根结点的层数为1，具有n个结点的满二叉树的深度为h=log2(n+1)

3.2完全二叉树

概念：棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

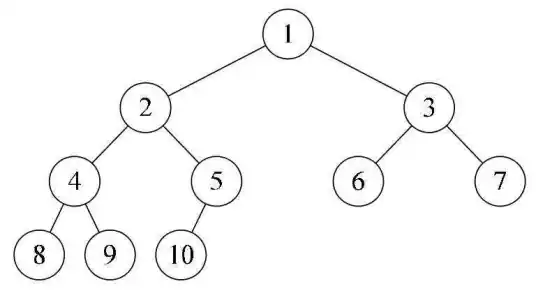
完全二叉树是由满二叉树引出来的。
特性：

• 除了最后一层，其他每层结点个数都达到最大
• 结点从左到右依次排列

可以说满二叉树包含于完全二叉树。
完
主页还有更多优质内容OvO