【LeetCode热题100道笔记】二叉树的右视图

题目描述

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

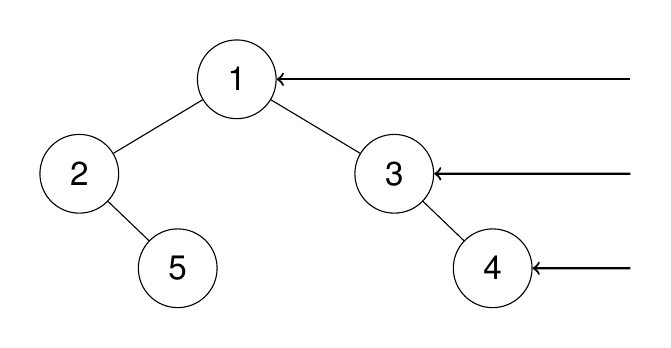
输入：root = [1,2,3,null,5,null,4]
输出：[1,3,4]
解释：

示例 2：
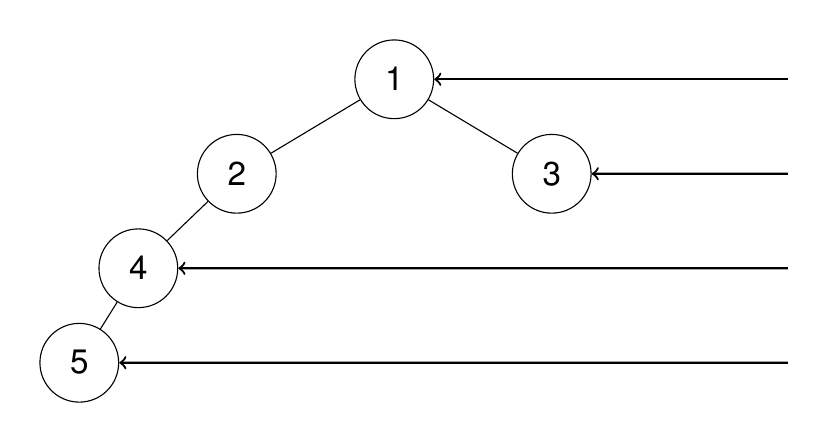
输入：root = [1,2,3,4,null,null,null,5]
输出：[1,3,4,5]
解释：

示例 3：
输入：root = [1,null,3]
输出：[1,3]

示例 4：
输入：root = []
输出：[]

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100

思考：层次遍历+取层尾节点

核心是用队列维护每一层节点，遍历每层时直接提取最后一个节点的值加入结果——因层次遍历按“左→右”顺序收集下一层节点，层尾节点天然是该层最右侧节点，无需额外判断。

算法过程

1. 边界处理：若根节点root为null（空树），直接返回空结果数组。
2. 初始化：创建结果数组result（存储右视图节点值），队列queue初始存入根节点（第一层仅根节点）。
3. 层序循环（遍历每一层）：
   • 记录当前层节点数：用size = queue.length获取当前层总节点数（避免后续队列添加子节点后长度变化）；
   • 取层尾节点值：当前层最右侧节点是队列第size-1个元素，将其val加入result；
   • 收集下一层节点：创建临时数组tmp，遍历当前层所有节点，按“左子节点→右子节点”顺序加入tmp（保证下一层节点仍按左→右排列，层尾为最右侧节点）；
   • 更新队列：将队列替换为tmp（下一层节点），进入下一轮循环，直至队列为空。
4. 返回结果：返回result，即二叉树右视图的节点值列表。

时空复杂度

• 时间复杂度：O(n)，n为二叉树节点总数。
  原因：每个节点仅入队、出队各1次，取层尾节点值的操作也为O(n)，总操作次数与节点数线性相关。
• 空间复杂度：O(m)，m为二叉树最宽层的节点数。
  原因：队列需存储当前层所有节点，最坏情况（完全二叉树最后一层）m=O(n/2)=O(n)，最好情况（链状树，每层仅1个节点）m=1。

代码

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[]}*/
var rightSideView = function(root) {const result = [];if (!root) return result; // 空树返回空数组let queue = [root]; // 队列：维护当前层节点while (queue.length) {const size = queue.length; // 固定当前层节点数（避免后续添加子节点影响）// 取当前层最后一个节点（最右侧节点）的值，加入结果result.push(queue[size - 1].val);// 收集下一层节点（左→右顺序，保证下一层层尾仍为最右侧节点）let tmp = [];for (let node of queue) {if (node.left) tmp.push(node.left);if (node.right) tmp.push(node.right);}queue = tmp; // 切换到下一层}return result;    
};

关键逻辑解析

1. 为何按“左→右”收集下一层节点？
   无论收集顺序是左→右还是右→左，只要能准确找到“当前层最后一个节点”即可。按左→右收集是层次遍历的常规习惯，且无需额外调整顺序——队列中当前层的最后一个元素，就是该层从右往左看的第一个可见节点。

2. 为何要固定当前层节点数size？
   若不固定size，直接遍历queue时，后续添加的下一层节点会混入当前层队列，导致遍历范围错误。用size = queue.length提前锁定当前层节点数，确保仅遍历当前层节点，避免逻辑混乱。

3. 对比深度优先（DFS）实现的优势
   层次遍历（BFS）的优势是“按层处理”，天然适合“取层尾节点”的需求，代码逻辑直观，无需维护深度参数；而DFS（如先右后左的前序遍历）需记录当前节点深度，仅在“首次访问该深度”时记录节点值，逻辑稍复杂。两种方法时间复杂度均为O(n)，空间复杂度相近，但层次遍历更贴合右视图的“层特性”。