【Day 22】94.二叉树的中序遍历 104.二叉树的最大深度 226.翻转二叉树 101.对称二叉树
文章目录
- 94.二叉树的中序遍历
- 题目:
- 思路:
- 代码实现(Go):
- 104.二叉树的最大深度
- 题目:
- 思路:
- 举例:
- 代码实现(Go):
- 226.翻转二叉树
- 题目:
- 思路:
- 举例:
- 代码实现(Go):
- 101.对称二叉树
- 题目:
- 思路:
- 举例:
- 代码实现(Go):
94.二叉树的中序遍历
题目:
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
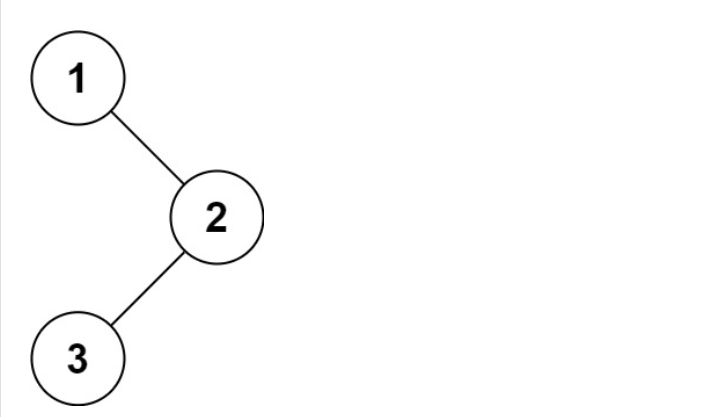
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
思路:
-
递归法:
-
定义一个函数
dfs(node):- 如果节点为空,返回。
- 递归遍历左子树。
- 访问当前节点值。
- 递归遍历右子树。
-
把访问的结果存到一个切片
res中。 -
时间复杂度
O(n),空间复杂度取决于递归深度,最坏O(n)。
-
-
迭代法(栈模拟):
-
用一个栈来模拟递归过程:
- 从根节点出发,不断把左子节点入栈。
- 当不能再往左时,出栈一个节点,访问它的值。
- 再转到该节点的右子树。
-
时间复杂度同样是
O(n),空间复杂度O(n)。
-
代码实现(Go):
递归:
package mainimport "fmt"type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}func inorderTraversal(root *TreeNode) []int {res := []int{}var dfs func(node *TreeNode) // 定义了一个函数类型的变量 dfsdfs = func(node *TreeNode) { // 给 dfs 赋值一个匿名函数(递归函数)if node == nil {return // 空节点直接返回}dfs(node.Left) // 递归访问左子树res = append(res, node.Val) // 访问当前节点dfs(node.Right) // 递归访问右子树}dfs(root) // 从根节点开始递归return res
}func main() {// root = [1,null,2,3]root := &TreeNode{Val: 1}root.Right = &TreeNode{Val: 2}root.Right.Left = &TreeNode{Val: 3}fmt.Println(inorderTraversal(root)) // 输出 [1,3,2]
}
迭代:
func inorderTraversal(root *TreeNode) []int {res := []int{}stack := []*TreeNode{} // 用切片模拟栈// 当 root 不为空,或者栈中还有未处理的节点时继续for root != nil || len(stack) > 0 {// 一直往左子树走,把沿途节点入栈for root != nil {stack = append(stack, root) // 压栈root = root.Left // 移动到左孩子}// 到达最左端,取栈顶节点(左子树都处理完了)root = stack[len(stack)-1] // 取出栈顶stack = stack[:len(stack)-1] // 出栈// 访问当前节点res = append(res, root.Val)// 转向右子树(可能为空,如果为空会在下一轮继续弹栈)root = root.Right}return res
}104.二叉树的最大深度
题目:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
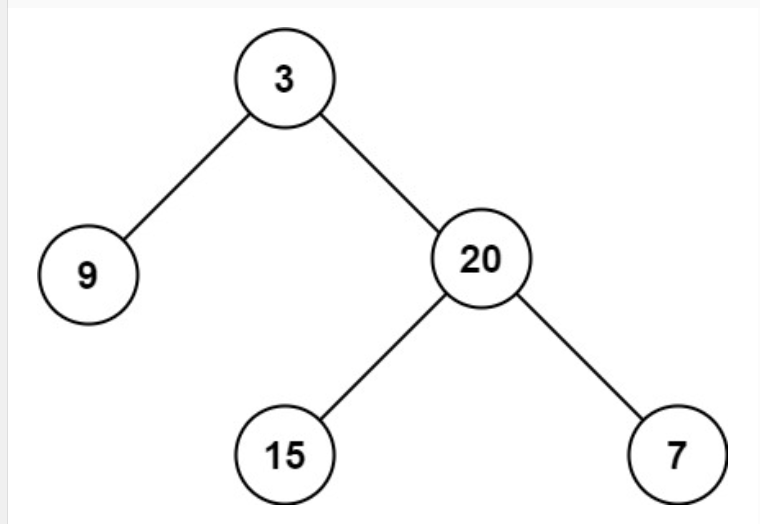
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
树中节点的数量在 [0, 10^4] 区间内。
-100 <= Node.val <= 100
思路:
-
递归定义:
- 对任意节点
node:
maxDepth(node) = max(maxDepth(node.Left), maxDepth(node.Right)) + 1- +1 是算上当前节点。
- 对任意节点
-
递归终止条件:
- 如果
node == nil,说明越过了叶子节点,深度为 0。
- 如果
-
整体逻辑:
- 先计算左子树深度
- 再计算右子树深度
- 取较大值 + 1
这就是 自底向上计算最大深度的思路。
举例:
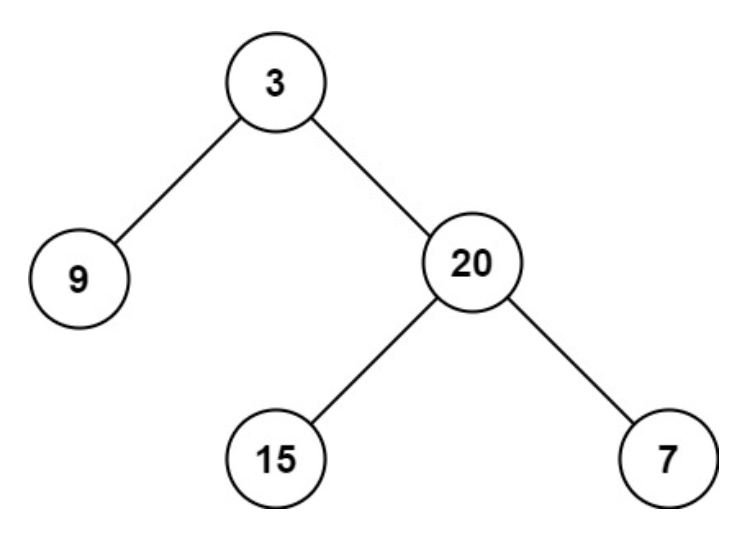
-
左子树
maxDepth(9)→ 叶子节点 → 返回 1 -
右子树
maxDepth(20)- 左子树
maxDepth(15)→ 返回 1 - 右子树
maxDepth(7)→ 返回 1 - 当前节点 20 的深度 =
max(1,1)+1 = 2
- 左子树
-
当前节点 3 的深度 =
max(1,2)+1 = 3
最终结果:3
-
时间复杂度:O(n)
- 每个节点访问一次,n = 节点数
-
空间复杂度:O(h)
- 递归栈的空间,h = 树的高度
- 最坏情况下(链式结构)空间复杂度 O(n)
代码实现(Go):
package mainimport "fmt"type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}func maxDepth(root *TreeNode) int {if root == nil {return 0 // 递归终止条件:空节点深度为0}return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}// 3
// / \
// 9 20
// / \
// 15 7func main() {root := &TreeNode{Val: 3}root.Left = &TreeNode{Val: 9}root.Right = &TreeNode{Val: 20}root.Right.Left = &TreeNode{Val: 15}root.Right.Right = &TreeNode{Val: 7}depth := maxDepth(root)fmt.Println(depth)
}226.翻转二叉树
题目:
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
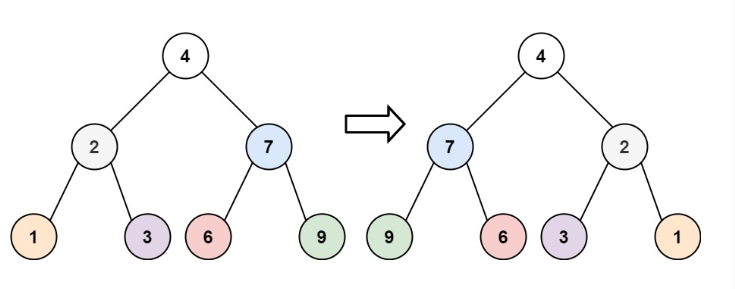
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
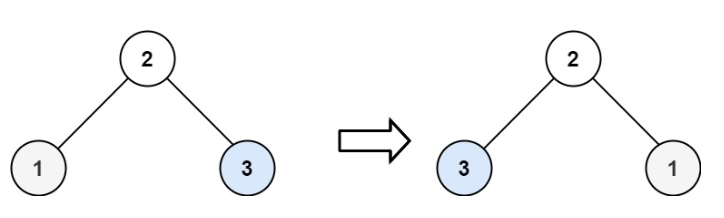
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
思路:
翻转二叉树 就是把每个节点的左右子树交换。
-
递归:
- 如果节点为空,直接返回
nil。 递归翻转左子树和右子树。交换当前节点的左右子树。- 返回
当前节点。
- 如果节点为空,直接返回
-
特点:
- 时间复杂度:
O(n),遍历每个节点一次。 - 空间复杂度:
O(h),递归栈高度为树的高度h,最坏为O(n)。
- 时间复杂度:
举例:
3/ \9 20/ \15 7
翻转过程(递归):
-
根节点 3
- 翻转左子树 9 → 返回 9(叶子节点
交换两个nil之后返回该叶子结点) - 翻转右子树 20
- 翻转左子树 9 → 返回 9(叶子节点
-
右子树节点 20
- 翻转左子树 15 → 返回 15
- 翻转右子树 7 → 返回 7
- 交换左右子树 → 20 的左右变为 7 和 15
-
根节点 3
- 交换左右子树 → 左子树变为 20,右子树变为 9
翻转后的二叉树:
3/ \20 9/ \7 15
核心思路:
递归翻转左右子树 → 交换左右节点 → 返回当前节点类似“自底向上”,叶子节点先返回,父节点再交换
代码实现(Go):
func invertTree(root *TreeNode) *TreeNode {if root == nil {// 如果当前节点为空,直接返回 nilreturn nil}left := invertTree(root.Left) // 递归翻转左子树right := invertTree(root.Right) // 递归翻转右子树// 交换左右子树root.Left = rightroot.Right = leftreturn root
}101.对称二叉树
题目:
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
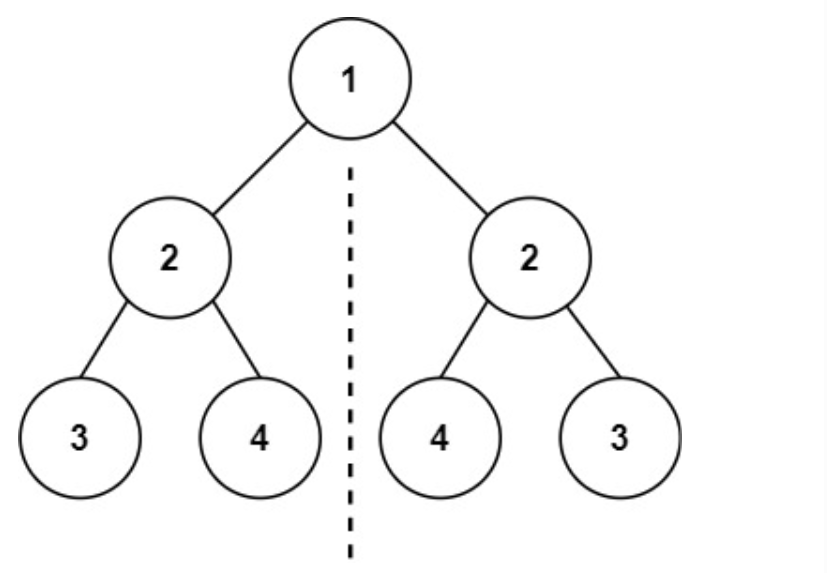
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
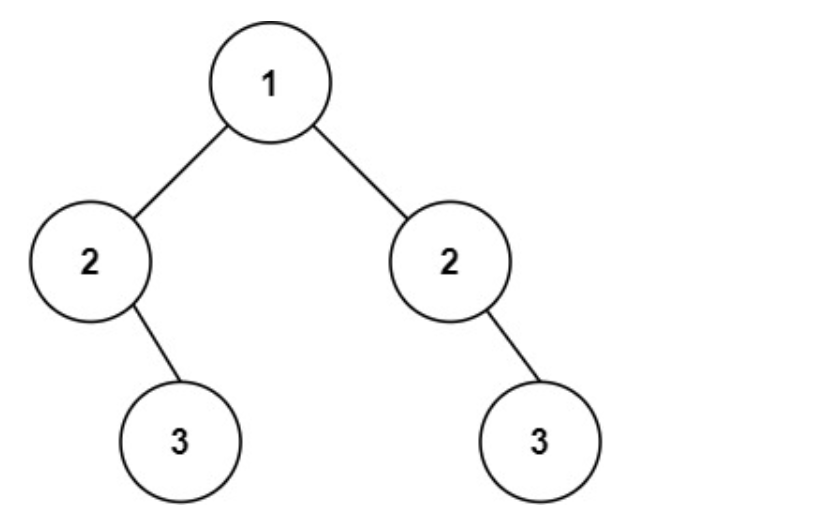
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
思路:
二叉树轴对称意味着左子树是右子树的镜像。
换句话说,对于树的根节点 root:
root.Left的左子树应该等于root.Right的右子树root.Left的右子树应该等于root.Right的左子树
我们可以用递归来判断两个子树是否互为镜像:
- 树为空 → 对称
- 如果两个子树都为空 → 对称
- 如果其中一个为空,另一个不为空 → 不对称
- 如果两个节点值不同 → 不对称
- 否则递归判断:
- 左子树的左节点 vs 右子树的右节点
- 左子树的右节点 vs 右子树的左节点
举例:
1/ \2 2/ \ / \3 4 4 3
调用 isSymmetric(root) → 递归检查左右子树是否镜像:
根节点 1
-
左子树
p = 2 -
右子树
q = 2 -
判断
p.Val == q.Val→ 2 == 2 -
继续递归:
只有当两个节点都不为空且值相等时,才继续递归判断它们的子树是否对称p.Leftvsq.Right→ 3 vs 3p.Rightvsq.Left→ 4 vs 4
左右对应节点
-
左子树的左节点 3 vs 右子树的右节点 3
- 都是叶子节点 → 左右子树都是 nil → 返回 true
-
左子树的右节点 4 vs 右子树的左节点 4
- 都是叶子节点 → 左右子树都是 nil → 返回 true
- 回到节点 2 → 左右镜像都成立 → 返回 true
3. 回到根节点 1
- 左右子树镜像都成立 → 返回 true
-
判断对称的核心逻辑:左右节点值相等,且左右子树互为镜像
-
类似最大深度递归:
先递归到叶子节点(自底向上)再逐层返回判断- 递归里的三步判断是
“当前节点层面”的判断,- 这三步判断的是当前节点 p 和 q 是否可能对称
- 如果不对称(例如值不同或者只有一个为空),递归直接返回 false
- 这部分可以看作
剪枝,避免不必要的递归
-
叶子节点比较时左右都是 nil → 返回 true(安全)
代码实现(Go):
package mainimport "fmt"type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}// 主函数:判断是否对称
func isSymmetric(root *TreeNode) bool {if root == nil {return true // 树为空 → 对称}return check(root.Left, root.Right)
}// 辅助函数:判断两棵树是否对称
func check(p, q *TreeNode) bool {if p == nil && q == nil { // 两个节点都为空 -> 对称return true}if p == nil || q == nil { // 一个为空,一个不为空 -> 不对称return false}if p.Val != q.Val { // 两个节点值不同 -> 不对称return false}// 只有当两个节点都不为空且值相等时,才继续递归判断它们的子树是否对称// 递归判断左右子树是否对称return check(p.Left, q.Right) && check(p.Right, q.Left)
}// 1
// / \
// 2 2
// / \ / \
// 3 4 4 3func main() {root := &TreeNode{Val: 1,Left: &TreeNode{Val: 2,Left: &TreeNode{Val: 3},Right: &TreeNode{Val: 4},},Right: &TreeNode{Val: 2,Left: &TreeNode{Val: 4},Right: &TreeNode{Val: 3},},}fmt.Println(isSymmetric(root)) // 输出 true
}