【论文阅读】InnerGS: Internal Scenes Rendering via Factorized 3D Gaussian Splatting

InnerGS: Internal Scenes Rendering via Factorized 3D Gaussian Splatting

基于分解式 3D 高斯溅射的室内场景渲染

原文链接：InnerGS: Internal Scenes Rendering via Factorized 3D Gaussian Splatting

摘要：

3D 高斯溅射（3D Gaussian Splatting，简称 3DGS）近年来在高效场景渲染领域备受关注，其核心原理是将场景表示为一组显式的各向异性 3D 高斯分布。然而，目前大多数相关研究工作主要聚焦于对物体外部表面的建模。在本研究中，我们将目标定为室内场景重建—— 这一方向对于需要深入理解物体内部结构的应用而言至关重要。通过利用内部 3D 高斯分布直接对连续的体密度进行建模，我们提出的模型能够从稀疏的切片数据中，高效重建出兼具平滑性与细节的内部结构。此外，该方法无需依赖相机姿态信息，具备 “即插即用” 的特性，并且本质上可兼容各类数据模态。

作者给出了代码地址，但是还没有公开，静静等待。。。
代码地址

结论：

在本研究中，我们提出了一种针对室内场景建模的 3D 高斯溅射（3DGS）新型扩展方法 —— 该任务对于医学成像、机器人技术、体分析等应用而言至关重要。目前，仍有多个极具探索价值的方向可供未来研究深入开展。通过我们提出的方法实现的高保真体重建，有望为后续的临床任务（如目标检测或图像分割）提供支持。

介绍：

在虚拟现实、机器人技术和医学成像等应用的推动下，三维（3D）重建已成为计算机视觉与图形学领域的核心研究方向。近年来，神经辐射场（Neural Radiance Fields，简称 NeRF）等方法彻底改变了 3D 场景捕捉技术，能够从二维（2D）图像中实现新视角合成与精细化场景表示。NeRF 模型通过神经网络学习，将场景表示为一个连续的体积场，在视角合成与几何重建方面展现出极高的灵活性。然而，利用 NeRF 实现高视觉质量往往需要复杂的多层感知器（multi-layer perceptrons），这类模型不仅训练成本高昂，渲染速度也较慢 [Kerbl 等人，2023]。这些局限性促使研究人员不断探索更高效的 3D 表示与渲染技术。

一种新兴的解决方案是 3D 高斯溅射（3D Gaussian Splatting，简称 3DGS），该技术近年来因实现快速神经渲染而备受关注。与依赖深度网络对场景进行隐式编码的方法不同，3DGS 通过一组显式的各向异性 3D 高斯分布来表示场景。关键在于，这种方法实现了速度上的突破：它能够达成 1080p 分辨率的实时新视角渲染（≥30 帧 / 秒），并将训练时间从数小时大幅缩短至数分钟。3DGS 兼具神经辐射场在高质量、连续重建方面的优势，以及基于点的渲染和稀疏计算所带来的效率，从而在 3D 场景重建与视角合成领域树立了新的技术标杆。

尽管 3D 高斯溅射（3D Gaussian Splatting，简称 3DGS）传统上主要面向外部视角合成，但当前研究正越来越多地聚焦于一项更复杂的挑战 —— 物体内部结构建模。这项任务标志着研究方向从 “表面补全” 向 “体积推断” 的根本性转变，而这对于需要深入理解物体内部结构的应用而言至关重要。例如，在医学成像领域，精细化的内部重建对疾病诊断与手术规划起着关键作用 [Wang 等人，2025]；在机器人技术与虚拟现实（VR）领域，该技术同样不可或缺 —— 这些系统需掌握物体的构成信息，才能实现真实的操作与交互 [Qiu 等人，2024；Zhu 等人，2024]。为应对这一挑战，研究人员正开发各类创新技术。在医学成像方向，基于物理的衰减模型（辐射场会被特定组织的衰减系数调制）已为 CT 重建质量带来了显著提升 [Zha 等人，2024]；而在另一研究方向，将深度扩散模型与自增强策略融入 3DGS 流程，或许能突破稀疏视角数据的局限性 —— 通过提供额外的伪监督信号，提升内部纹理的合成效果 [Wu 和 Chen，2024]。

然而，该领域仍面临诸多重大挑战。当前大多数方法专为 X 射线或 CT 投影数据设计，难以推广至其他数据模态，如核磁共振（MRI）、功能性核磁共振（fMRI）或其他大规模 3D 遥感数据。此外，这些方法严重依赖外部视角，其重建结果要么缺失精细的内部细节，要么需要复杂的正则化处理，而这会模糊细微结构。最后，许多混合训练方法依赖深度多层感知器（MLPs）或逐视角扩散优化，导致推理速度无法达到实时水平，也增加了扩展构建的难度。

为解决上述局限性，我们提出了一种专为室内场景建模设计的新型方法 —— 该方法采用 3D 高斯密度，而非传统的基于投影的 2D 高斯渲染。具体而言，我们首先在每个深度切片上计算条件 2D 高斯溅射，以确定图像平面内 2D 高斯的中心与影响半径；随后，将这些条件 2D 高斯与沿深度轴分布的边缘 1D 高斯相结合，构建出完整的 3D 高斯溅射（3DGS）密度。这种设计使我们能够执行与 3DGS 相同的基于瓦片的光栅化过程，从而实现从稀疏切片数据中重建出兼具平滑性与细节的内部结构。

本文的贡献如下：

• 提出了“内部高斯溅射”框架，该框架利用3D高斯溅射来实现直接的体积推断。这种新颖的方法能够从稀疏、无位姿的切片数据中，高保真地重建复杂的内部结构。
• 提出了一种以“条件溅射”为核心的高效、基于切片的渲染流程。与启发式投影方法相比，该技术能为每个2D切片动态调整高斯分布的采样方式，从而提高计算效率和重建精度。
• 提供了该解决方案的即插即用型CUDA实现。此外，我们还在多个医学数据集上验证了该方法的有效性。该框架能够重建大脑和心脏核磁共振成像（MRI）等静态场景，以及手腕运动和大脑功能性核磁共振成像（fMRI）数据等4D动态序列。

相关工作

从稀疏视角进行新视角合成 Novel View Synthesis from Sparse Views

3D高斯溅射（3D Gaussian Splatting，简称3DGS）已成为新视角合成领域极具竞争力的方法[Kerbl 等人，2023]。然而，3DGS的重建质量极大程度上依赖于输入视角的质量，这使得它在视角稀疏或无位姿（unposed）的场景下表现不佳。为应对这些挑战，相关研究陆续提出解决方案：例如“COLMAP-Free”方法[Fu 等人，2024]；此外，还有一类端到端方法，通过隐式神经表示直接从稀疏输入中预测3D高斯参数，这类方法包括Gamba[Shen 等人，2024]、Splatter Image[Szymanowicz 等人，2024]和pixelSplat[Charatan 等人，2024]——它们均结合了U-Net骨干网络、Transformer模块与注意力机制，以回归出高斯中心、不透明度及空间参数。另有研究将扩散模型融入3DGS流程，在稀疏监督条件下生成新视角（hallucinate novel views）或优化几何结构。例如Posediffusion（原文未标注文献）、DreamGaussian[Tang 等人，2024]、Deceptive-NeRF/3DGS[Liu 等人，2024]等框架，会将扩散模型生成的视角纳入训练过程，从而在稀疏视角场景下提升重建结果的视觉保真度。

现有研究已将其拓展至稀疏视角和单视角场景，但针对带切片数据的稀疏视角场景，相关研究十分有限。这类场景存在本质上不同的挑战，需要进行体积推断而非表面补全。我们的工作通过从切片重建密集内部结构且不依赖多视角位姿，填补了这一空白。

使用神经辐射场（NeRF）和三维高斯溅射（3DGS）进行内部结构重建 Internal Structure Reconstruction with NeRF and 3DGS

内部结构重建旨在通过外部二维（2D）图像还原物体隐藏的体积细节。在医学成像领域，MedNeRF方法[Corona-Figueroa 等人，2022]对神经辐射场（NeRF）进行了适配，可从单张X射线图像中重建具备3D感知能力的CT投影，并引入物理先验知识以捕捉组织的衰减特性。类似地，NAF方法[Zha 等人，2022]将3D衰减建模为连续的神经场，同时利用自监督判别器与数据增强技术，从单张X射线图像生成高质量的3D感知CT投影。SAX-NeRF方法[Cai 等人，2024b]则引入了基于线段的Transformer（Line Segment-based Transformer）与专用的射线采样策略，用于稀疏视角X射线重建，进而提升了从有限视角中捕捉内部结构细节的能力。Wang等人[2025]的综述文章全面回顾了神经辐射场（NeRF）的发展历程，并重点强调了其在体积重建与内部结构重建领域的适配应用。

“高斯薄饼”（Gaussian Pancakes，Bonilla 等人，2024）方法引入了几何正则化的溅射技术，用于实现逼真的内窥镜重建，证明了3D高斯溅射（3DGS）在人体内部解剖结构建模中的适用性。同样地，“多层高斯溅射”（Multi-Layer Gaussian Splatting，Kleinbeck 等人，2024）方法探索了沉浸式解剖结构可视化，展示了分层高斯表示如何捕捉内部结构。近期的创新成果还包括“水果忍者”（FruitNinja，Wu 和 Chen，2024）方法——该方法利用高斯溅射技术，在对物体进行虚拟切片时生成其内部纹理。在医学应用方向，“X射线高斯”（X-Gaussian，Cai 等人，2024a）方法用辐射强度响应函数（RIRFs）替代了球谐函数，以建模X射线衰减的各向同性特性；与基于神经辐射场（NeRF）的方法相比，该方法实现了更快的推理速度和更优的图像质量。“深度动态高斯溅射”（DDGS，Gao 等人，2024）方法则通过将各向同性衰减与散射、射线硬化等微弱各向异性效应分离，进一步优化了辐射建模。借助结构先验知识，“X射线高斯辐射建模”（X-GRM，Liu 等人，2025）方法将高斯中心固定在体素网格上，同时通过Transformer网络学习辐射属性，最终实现了稳定的收敛效果，并在稀疏视角CT重建任务中取得了更优性能。

然而，现有研究主要聚焦于 X 射线和 CT 数据，难以推广并适配多种数据模态，包括但不限于核磁共振（MRI）、功能性核磁共振（fMRI）、激光雷达（LiDAR）以及点云数据。与之不同的是，我们的方法具备 “即插即用” 特性，且在与现有 3D 高斯溅射（3DGS）应用集成方面具有巨大潜力。

方法

我们提出的方法构建了一种具备照片级真实感的场景表示方式，专门针对内部细节丰富的场景设计。本节内容安排如下：3.2 节将介绍我们提出的 “内部 3D 高斯溅射”（Inner 3D Gaussian Splatting）框架 —— 该框架通过对体积密度建模，实现从稀疏切片中重建内部结构；3.3 节将阐述渲染与优化流程。整个方法流程的概览图如图 1 所示。

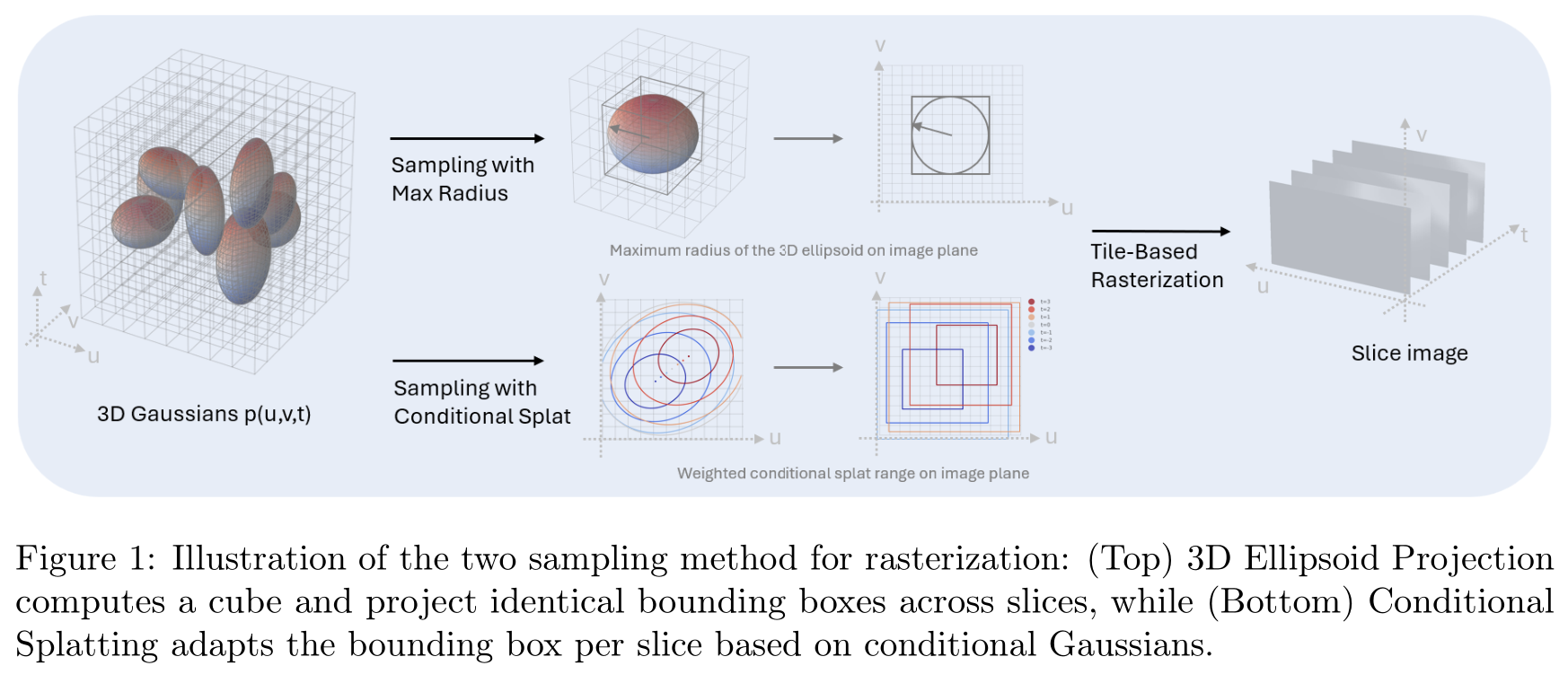
图 1：两种光栅化采样方法示意图：（上）3D 椭球投影法先计算一个立方体，再在各切片上投影相同的边界框；（下）条件溅射法则基于条件高斯分布，为每个切片适配对应的边界框。

3.1 Preliminary: 3D Gaussian Splatting 预备知识：3D 高斯溅射（3DGS）

在三维高斯溅射（3D Gaussian Splatting）中，一个场景被表示为一团三维高斯分布的集合。每个高斯分布在理论上具有无限的作用范围，它对给定空间位置$\mathbf{x}\in {\mathbb{R}}^3$的影响由一个未归一化的高斯函数定义：

$$p(\mathbf{x})=e^{-\frac{1}{2}(\mathbf{x}-\mu {)}^T{\Sigma }^{-1}(\mathbf{x}-\mu )},\text{\hspace{1em}(1)}$$
在这种设定下，每个高斯分布的位置由向量$\mu =({\mu }_x,{\mu }_y,{\mu }_z)$表示。其协方差矩阵$\Sigma$被分解为缩放分量和旋转分量，表达式为$\Sigma =RS{S}^{\top }{R}^{\top }$，其中$S$是一个对角矩阵，包含缩放因子$s_x$、$s_y$和$s_z$，而$R$由编码旋转的单位四元数$q$推导而来。此外，每个三维高斯分布还包含球谐函数（Spherical Harmonics，SH）的系数，用于建模与视角相关的颜色变化，以及一个不透明度参数$\alpha$。这些参数在训练过程中通过最小化渲染损失来联合优化。

3.2 用于内部场景的三维高斯技术

Problem formulation

在标准的三维高斯溅射（3DGS）框架中，每个高斯分布都会被投影到二维图像平面上。这种投影会生成一个二维椭圆形溅射点，其均值和协方差矩阵是由经相机视图矩阵和投影矩阵变换后的三维高斯分布推导得出的。设图像平面上的像素坐标为$(u,v)$，对于宽度为$W$、高度为$H$的图像，$u$的取值范围是$[0,W-1]$，$v$的取值范围是$[0,H-1]$。第$i$个溅射点在像素$(u,v)$处的屏幕空间贡献，通过密度$p_i(u,v)$乘以其不透明度${\alpha }_i$和颜色$c_i$来计算。高斯分布按照从前到后的顺序进行渲染，通过累积颜色和不透明度来生成最终的像素颜色，具体如公式(2)所示，其中$N$表示高斯分布的总数。

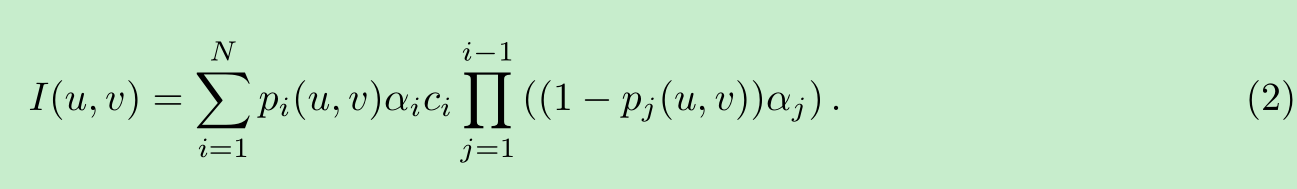
然而，这种基于投影的机制从根本上不适合对内部体结构进行建模，主要有两个原因。首先，学习得到的高斯分布集中在物体表面，使得内部体区域大多为空或未定义。其次，基于投影的渲染管线依赖于相机参数（视图矩阵和投影矩阵），而切片数据中并不存在这些参数。因此，将原始的三维高斯溅射（3DGS）方法应用于稀疏切片数据时，无法捕捉切片之间连续的体信息，从而导致内部表示不完整。

Representation of Inner 3D Gaussian

为了克服这些限制，我们的目标是定义一种可以直接对体积密度进行建模的场景表示。我们考虑二维切片上的任意像素 $(u,v)$，其中该切片位于给定轴上深度为 $t$ 的位置。我们不再依赖投影，而是计算每个高斯对像素的贡献 $p_i(u,v,t)$，因此，像素的最终颜色计算如下：

$$I(u,v,t)=\sum _{i=1}^N{p}_i(u,v,t){\alpha }_i{c}_i\prod _{j=1}^{i-1}(1-p_j(u,v,t){\alpha }_j)$$
通过这个公式，我们直接对连续的体积密度进行建模，从而能够在任意深度合成新的切片。这种内部三维表示方法结合了连续（类似神经辐射场 NeRF）和离散建模（类似网格 Mesh）的优点：高斯的连续性允许无缝的体积插值，能够重建平滑且详细的内部结构。同时，将体积表示为离散的高斯集合提供了一种明确且可解释的表示形式，使该方法高效且适用于医学成像等应用。

公式解析. 像素贡献计算
- 在二维切片上考虑像素 $(u,v)$，切片处于给定轴上深度 $t$ 的位置。与之前基于投影计算溅射点对像素贡献不同，这里直接计算每个高斯 $i$ 对像素 $(u,v)$ 在深度 $t$ 处的贡献 $p_i(u,v,t)$。
- 像素的最终颜色 $I(u,v,t)$ 是通过一个公式计算得出。公式中，${\sum }_{i=1}^N$ 表示对 $N$ 个高斯进行求和，$p_i(u,v,t){\alpha }_i{c}_i$ 体现了第 $i$ 个高斯对像素颜色的基础贡献（涉及密度 $p_i$、不透明度 ${\alpha }_i$ 和颜色 $c_i$），而 ${\prod }_{j=1}^{i-1}(1-p_j(u,v,t){\alpha }_j)$ 这一部分则考虑了前面 $j$ 个高斯对当前高斯贡献的遮挡或混合影响。
3. 新表示方法的优势
- 连续体积密度建模：通过上述公式可以直接对连续的体积密度进行建模，这使得能够在任意深度 $t$ 合成新的切片，为更灵活地处理内部结构提供了可能。
- 结合连续与离散建模优点
- 连续性优势：高斯分布的连续性允许进行无缝的体积插值，这对于重建物体内部平滑且详细的结构非常有帮助，类似于神经辐射场（NeRF）在连续空间建模方面的优势。
- 离散性优势：将体积表示为离散的高斯集合，这种表示形式明确且可解释，相比一些复杂的连续场表示，该方法更加高效，并且特别适合医学成像等应用场景，类似于网格（Mesh）建模的直观性和可操作性。

3.3 Rendering and Optimization

在渲染过程中，三维高斯溅射（3DGS）避免在每个像素处计算所有高斯分布。相反，每个高斯分布被投影到图像平面上，形成一个二维椭圆形溅射点，并计算其3σ范围以定义一个边界框，用于确定重叠的像素。因此，对于每个像素，仅对一部分候选高斯分布进行采样，这大大降低了计算成本。为了在此实现高效的候选采样，我们提出了两种方法：三维椭球投影法和条件溅射法。

方法1：三维椭球投影

在此方法中，我们将三维高斯分布的范围近似为一个球体，该球体的半径由高斯椭球的最大轴长决定。对于协方差为$\Sigma$的高斯分布，椭球的主轴与$\Sigma$的特征向量对齐，并且主轴的长度由特征值的平方根给定（需按一个常数进行缩放）：

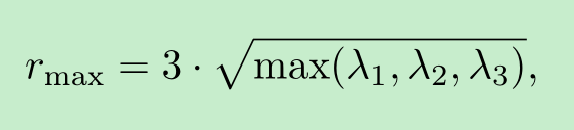
其中，${\lambda }_1$、${\lambda }_2$、${\lambda }_3$ 是协方差矩阵 $\Sigma$ 的特征值。以高斯分布的均值为中心，构建一个边长为 $2r_{max}$ 的立方体，并将该立方体正交投影到每个图像切片上。这样，在所有切片上会得到相同的二维边界框，如图1所示，但这可能会导致处理区域过大，产生冗余计算。

方法2：条件溅射

在第二种方法中，我们采用一种条件公式来计算每个高斯分布在各个切片上的范围，如图1底部所示。具体而言，我们通过分解的高斯结构将高斯分布上的点 $p_i(u,v,t)$ 溅射到给定深度 $t$ 的二维平面上：
$$p_i(u,v,t)=p_i(u,v|t)p_i(t)$$
其中，$p_i(u,v|t)$ 是一个条件二维高斯分布，用于描述在给定切片位置 $t$ 的情况下图像平面上的横向空间分布，而 $p_i(t)$ 是一个一维高斯分布，用于对深度轴上的不确定性或分布进行建模。如附录C所示，条件均值 ${\mu }_{u,v|t}$ 随切片深度 $t$ 变化，这反映出二维溅射中心在各切片间的移动。此外，通过引入与距离相关的缩放因子，二维溅射的范围会随着三维高斯中心与切片之间距离的增加而减小。与第一种方法（将同一个立方体边界框投影到每个切片上）不同，这种方法为每个切片计算一个适配的边界框，从而实现更高效的采样。

对于为每个像素采样的候选高斯分布集合，我们根据其中心与图像平面之间的距离对它们进行排序。通过差分光栅化过程，后续的优化流程与原始的三维高斯溅射（3DGS）方法保持一致，从而得到算法1中描述的完整训练算法。

附录 B Training Implementation

算法1描述了三维高斯溅射（3D Gaussian Splatting）的内部训练循环。它首先在三维网格上初始化高斯分布，然后使用梯度下降法对其参数进行迭代优化。在每一步中，该算法将高斯分布投影到不同的二维切片视图上，计算渲染结果和损失函数，并进行反向传播。此外，还会应用剪枝、致密化（增加高斯数量以填充区域）和克隆等步骤，以动态调整高斯分布的集合，从而提高场景重建质量。

这个算法描述了三维高斯溅射（3D Gaussian Splatting）的内部训练过程，旨在通过优化高斯分布的参数来实现对三维场景的高效重建。以下是对该算法的详细解读：

算法输入和初始化

1. 输入要求：

   • 训练切片 $\mathcal{D}=\{(I_i^{\text{axis}},{\pi }_i^{\text{axis}})\}$，其中 $I_i^{\text{axis}}$ 是二维切片图像，${\pi }_i^{\text{axis}}$ 是切片的位置。
   • 网格分辨率 $g_{\text{res}}$ 和最大迭代次数 $T_{\text{max}}$。
   • 不透明度、梯度和缩放的阈值 $({\tau }_{\alpha },{\tau }_p,{\tau }_s)$。

2. 初始化：

   • 构建一个大小为 $g_{\text{res}}^3$ 的规则网格 $\mathcal{P}$，或者使用SfM（Structure from Motion）估计的点。
   • 每个高斯分布的均值 $\mu$ 围绕网格点初始化，默认参数为 $(s,c,\alpha ,q)$。

优化过程

1. 优化器设置：使用Adam优化器，参数为 $\theta$ 和 $\eta$。
2. 迭代优化：
   • 对于每次迭代（从1到 $T_{\text{max}}$）：
     • 初始化总损失 $L_{\text{total}}$ 为0，并将梯度 $\nabla \theta$ 置零。
     • 对于每个坐标轴 {x,y,z}\{x, y, z\}{x,y,z}：
       • 对于每个切片 $(I_i^{\text{axis}},{\pi }_i^{\text{axis}})$：
         • 计算三维协方差矩阵 ${\Sigma }_n=R_n{S}_n{S}_n{R}_n^{\top }$。
         • 通过光栅化得到预测图像 $I_{\text{pred}}=\text{Rasterize}({\mu }_n,{\Sigma }_n,{\alpha }_n,c_n)$。
         • 计算损失 $L=\text{Loss}(I_{\text{pred}},I_i^{\text{axis}})$，并累加到总损失 $L_{\text{total}}$。
     • 执行反向传播，更新参数 $\theta$。

高斯分布的动态调整

1. 细化迭代检查：如果是细化迭代：
   • 对于所有高斯分布 $(\mu ,\Sigma ,c,\alpha )$：
     • 如果不透明度 $\alpha <{\tau }_{\alpha }$ 或者高斯分布过大（$\text{IsTooLarge}(\mu ,\Sigma )$），则移除该高斯分布（剪枝）。
     • 否则，如果梯度范数 $\Vert {\nabla }_{\mu }L{\Vert }_2>{\tau }_p$：
       • 如果协方差矩阵的Frobenius范数 $\Vert \Sigma {\Vert }_F>{\tau }_s$，则分裂该高斯分布（解决过度重建问题）。
       • 否则，克隆该高斯分布（解决重建不足问题）。

总结

该算法通过在三维空间中初始化高斯分布，并将其投影到二维切片上进行渲染和损失计算，利用梯度下降法优化高斯分布的参数。同时，通过剪枝、分裂和克隆等操作动态调整高斯分布的集合，以提高场景重建的质量。这种动态调整机制有助于在训练过程中更好地适应复杂的场景结构，避免过度重建或重建不足的问题。

附录 C Parameter of 2DGS and 1DGS

给定一个均值向量为 ${\mu }_{3D}=[{\mu }_x,{\mu }_y,{\mu }_z{]}^{\top }$、协方差矩阵为 ${\Sigma }_{3D}=[({\sigma }_{xx},{\sigma }_{xy},{\sigma }_{xz}),({\sigma }_{xy},{\sigma }_{yy},{\sigma }_{yz}),({\sigma }_{xz},{\sigma }_{yz},{\sigma }_{zz})]$ 的三维高斯分布，我们可以沿深度轴 $t$ 将其概率密度分解为因式形式。具体而言，我们将联合密度 $p(u,v,t)$ 分解为沿深度方向 $t$ 的边缘分布与给定 $t$ 时二维坐标 $(u,v)$ 的条件分布的乘积。

深度轴上的边际密度由下式给出：
$$p(t)\sim \mathcal{N}({\mu }_z,{\sigma }_{zz})$$

其中，${\mu }_z$ 和 ${\sigma }_{zz}$分别表示沿 $z$ 轴的高斯分布的均值和方差。

在特定深度 $t$ 的条件下，平面内坐标 $(u,v)$ 上的分布为高斯分布：

$$p(u,v\mid t)\sim \mathcal{N}({\mu }_{uv|t},{\Sigma }_{uv|t})$$

其中，条件均值${\mu }_{uv|t}$根据偏移量$t-{\mu }_z$ 线性移动：

$${\mu }_{uv|t}=\left[\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right]+\frac{t-{\mu }_z}{{\sigma }_{zz}}\left[\begin{array}{c}{\sigma }_{xz}\\ {\sigma }_{yz}\end{array}\right]=\left[\begin{array}{c}{\mu }_u\\ {\mu }_v\end{array}\right]$$

这种关系反映了当我们切片通过不同深度级别时，图像平面中高斯足迹的均值位置如何移动。

相应的条件协方差矩阵由下式给出：

$${\Sigma }_{uv|t}=\left[\begin{array}{cc}{\sigma }_{xx}& {\sigma }_{xy}\\ {\sigma }_{xy}& {\sigma }_{yy}\end{array}\right]-\frac{1}{{\sigma }_{zz}}\left[\begin{array}{c}{\sigma }_{xz}\\ {\sigma }_{yz}\end{array}\right]\left[\begin{array}{cc}{\sigma }_{xz}& {\sigma }_{yz}\end{array}\right]$$

该矩阵解释了当深度 $t$ 固定后，$u$ 和$v$ 方向上的不确定性如何减少。所得的条件分布在深度 $t$的切片上定义了一个二维椭圆高斯足迹，描述了三维高斯分布在该切片上如何投影到成像平面上。

因此，完整的三维高斯密度可以表示为以下乘积：

$$p(u,v,t)=p(t)\cdot p(u,v\mid t)$$

这提供了一种分解且计算高效的方式来对体数据建模，特别适用于基于切片的渲染或断层重建等应用，在这些应用中通常需要处理三维体积的单个平面。

附录 D Simulation on Gaussian Selection via Conditional Splat

为了进一步分析条件溅射（conditional splat）的准确性，我们将切片上的真实三维高斯等概率轮廓与条件溅射近似进行对比。我们生成一个三维高斯分布，并通过用固定切片与高斯密度相交来提取其真实等概率轮廓。然后，从相应的二维椭圆溅射（ellipse splat）计算条件溅射近似，并用边际因子进行缩放。

如图10所示，红色虚线轮廓（条件溅射）与蓝色实线轮廓（真实等概率）紧密重叠。这表明条件溅射为原始三维高斯的影响范围提供了准确且高效的近似。

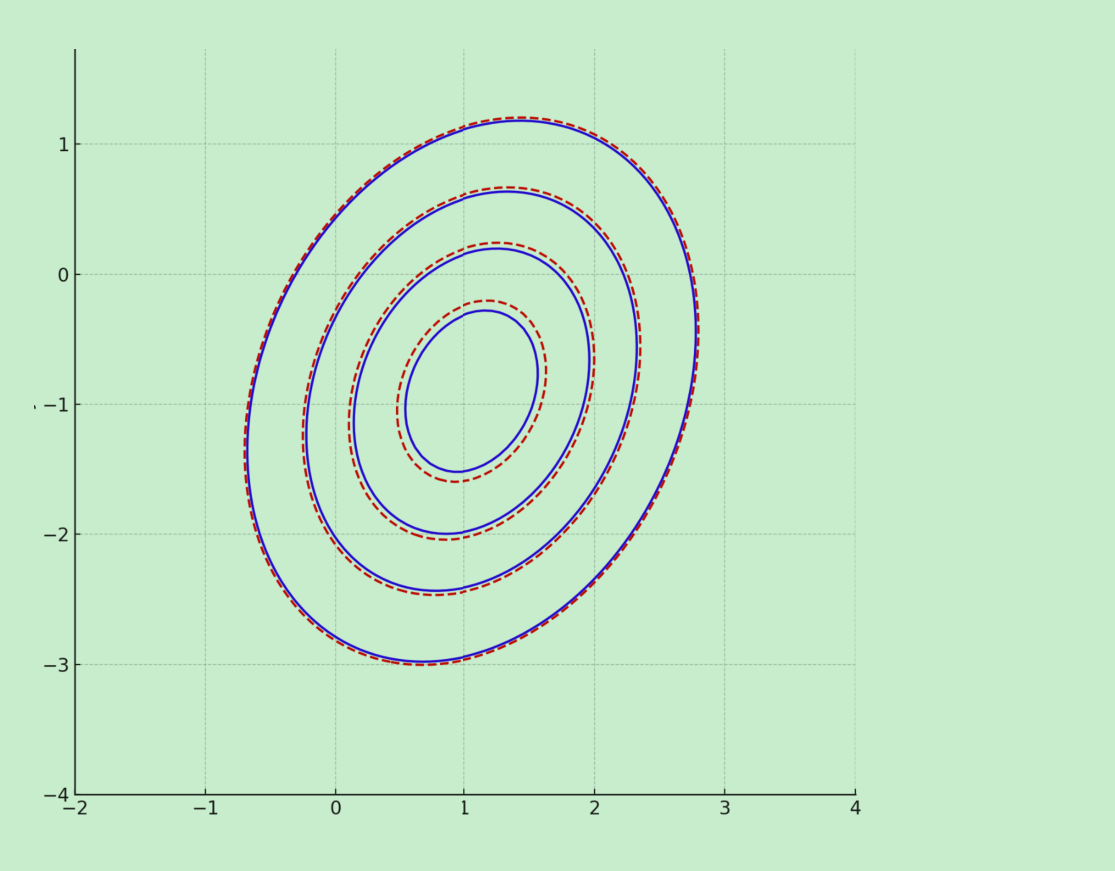
图10：条件溅射近似（红色虚线）与真实三维高斯等概率轮廓（蓝色实线）紧密匹配。