10.2 工程学中的矩阵(2)
十、例题
【例3】求由弹簧连接的 100100100 个质点的位移 u(1),u(2),...,u(100)u(1),u(2),...,u(100)u(1),u(2),...,u(100), 弹性系数均为 c=1c = 1c=1, 每个质点受到的外力均为 f(i)=0.01f(i)=0.01f(i)=0.01. 画出两端固定和固定-自由这两种情形 u 的图形。
解:
% 参数设置
n = 100; % 质点的数量
c = 1; % 弹性系数
f = 0.01*ones(n,1); % 每个质点受到的外力% 1. 两端固定边值条件
% 使用diag函数构造矩阵A
A0 = diag(ones(n+1, 1), 0)-diag(ones(n,1), -1); % A0是一个101*100的矩阵,这里创建一个101*101的矩阵
A0 = A0(:, 1:n); % 截取前100列即可得到矩阵A0% 构造刚度矩阵K
K_fixed = A0'*A0; % 由于弹性系数均为1,所以此处不含有矩阵C% 求解位移u
u_fixed = K_fixed \ f;% 绘制两端固定边值条件的位移图
figure(1);
plot(u_fixed, '+');
xlabel('mass number'); % 质点编号
ylabel('movement'); % 位移
title('两端固定边值条件的位移');
grid on;
print -dpng fixed_fixed_displacement.png;% 2. 固定-自由边值条件
% 构造矩阵 A
A1 = A0(1:n, :); % A1是一个方阵,取A0的前100行即可% 构造刚度矩阵K
K_free = A1'*A1;% 求解位移
u_free = K_free \ f;% 绘制固定-自由边值条件的位移图
figure(2);
plot(u_free, '+');
xlabel('mass number');
ylabel('movement');
title('固定-自由边值条件的位移');
grid on;
print -dpng fixed_free_displacement.png
运行结果:
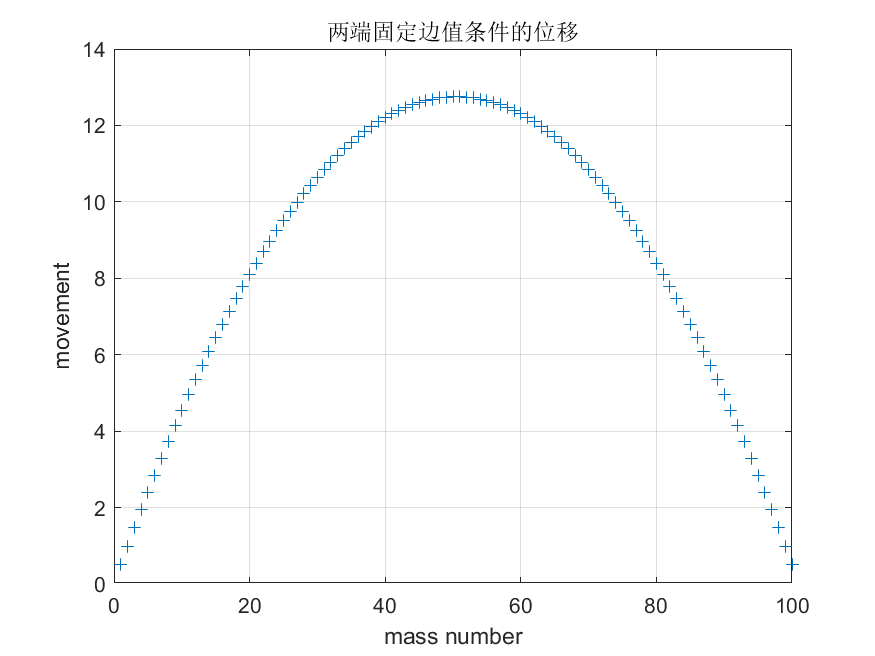 |  |
|---|
【例4】化学工程中通常用一阶导数 dudx\dfrac{\textrm du}{\textrm dx}dxdu 表示流体流速,用二阶导数 d2udx2\dfrac{\textrm
d^2u}{\textrm dx^2}dx2d2u 描述扩散速度。将 dudx\dfrac{\textrm du}{\textrm dx}dxdu 分别换成向前、中心差分和向后差分,取 Δx=18Δx = \dfrac{1}{8}Δx=81. 画出这三种离散方法求出的下面方程数值解的图形:
−d2udx2+10dudx=1,u(0)=u(1)=0.-\dfrac{\textrm d^2u}{\textrm dx^2} + 10\dfrac{\textrm du}{\textrm dx} = 1, \kern 5ptu(0) = u(1) = 0.−dx2d2u+10dxdu=1,u(0)=u(1)=0.
这种 对流-扩散方程(convection-diffsion equation) 无处不在,这个方程转化为描述期权定价问题的布莱克-斯科尔斯(Black-Scholes)方程。
解:
E = diag(ones(6,1),1); % 创建一个对角矩阵,用来辅助计算 K 和 D
K = 64 * (2*eye(7)-E-E'); % 计算二阶差分矩阵
D = 80 * (E-eye(7)); % 向前一阶差分矩阵
u = (K+D)\ones(7,1); % 向前差分求解x = linspace(0, 1, 9); % 区间[0,1]之间等间距9个点,则每段长度1/8 % 画出图形
figure;
plot(x, [0; u; 0], 'o-', 'DisplayName', 'Forward Difference'); % 绘制向前差分解的图像并标上图例, [0; u; 0] 是拼接列向量
hold on;
u = (K-D')\ones(7,1); % 向后差分
plot(x, [0; u; 0], 'd-', 'DisplayName', 'Backward Difference'); % 绘制向后差分解的图像并标上图例
u = (K+D/2-D'/2)\ones(7,1); % 中心差分
plot(x, [0; u; 0], 's-', 'DisplayName', 'Centred Difference'); % 绘制中心差分解的图像并标上图例
xlabel('x'); ylabel('u(x)'); % 坐标轴表示
title('Numrerical Solutions of Convection-Diffusion Equation'); % 图像标题
legend('Location', 'northwest'); % 图例在左上角
grid on;% 精确解计算:u(x) = 1/(10(e^{10}-1))(1-e^{10x})+x/10
e10 = exp(10);
A = 1/(10*(e10-1));
B = -1/(10*(e10-1));
u_exact = A + B * exp(10*x) + x/10;
plot(x, u_exact, 'k-', 'DisplayName', 'Exact Solution'); % 画出第2~8个点的精确解图像
hold off;
运行结果:

通常情况下,中心差分是最优解,它最接近精确解。
