二、感知机
因为感知机也是作为神经网络(深度学习)的起源的算法。因此,学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。
2.1 感知机是什么
感知机接收多个输入信号,输出一个信号。这里所说的“信号”可以想象成电流或河流那样具备“流动性”的东西。
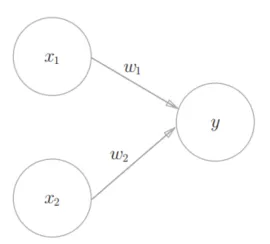
上图是一个接收两个输入信号的感知机的例子。x1、x2是输入信号,y是输出信号,w1、w2是权重(w是weight的首字母)。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时,会被分别乘以固定的权重(w1x1、w2x2)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活”。这里将这个界限值称为阈值,用符号θ表示。
感知机的运行原理只有这些!把上述内容用数学式来表示
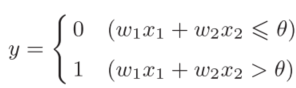
2.2 简单逻辑电路
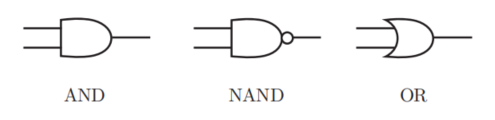
2.2.1 与门(AND gate)
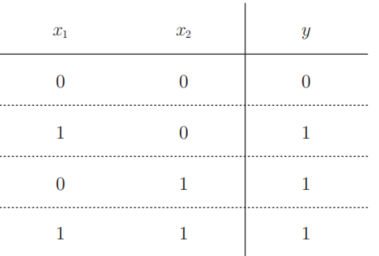
与门仅在两个输入均为1时输出1,其他时候则输出0。
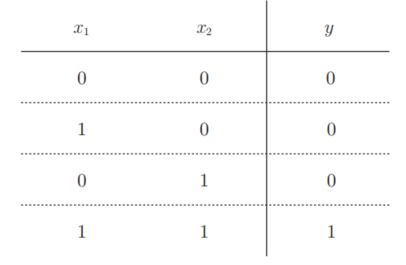
下面考虑用感知机来表示这个与门。需要做的就是确定能满足真值表的w1、w2、θ的值。
满足条件的参数的选择办法有很多。比如,当 (w1, w2, θ) = (0.5, 0.5, 0.7) 时,可以满足。此外,当 (w1, w2, θ) 为(0.5, 0.5, 0.8)或者(1.0, 1.0, 1.0)时,同样也满足与门的条件。设定这样的参数后,仅当x1和x2同时为1时,信号的加权总和才会超过给定的阈值θ。
2.2.2 与非门和或门
再来考虑一下与非门(NAND gate)。NAND是Not AND的意思,用真值表表示仅当x1和x2同时为1时输出0,其他时候则输出1。
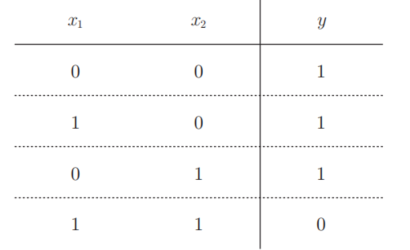
要表示与非门,可以用(w1, w2, θ) = (−0.5, −0.5, −0.7)这样的组合(其他的组合也是无限存在的)。
或门是“只要有一个输入信号是1,输出就为1”的逻辑电路。
那么我们来思考一下,应该为这个或门设定什么样的参数呢?
这里决定感知机参数的并不是计算机,而是我们人。我们看着真值表这种“训练数据”,人工考虑(想到)了参数的值。而机器学习的课题就是将这个决定参数值的工作交由计算机自动进行。学习是确定合适的参数的过程,而人要做的是思考感知机的构造(模型),并把训练数据交给计算机。
2.3 感知机的实现
2.3.1 简单的实现
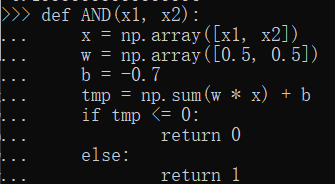
先定义一个接收参数x1和x2的AND函数
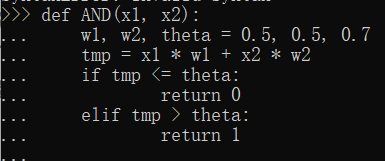
调用函数

这样我们就实现了与门。
2.3.2 导入权重和偏置
刚才的与门的实现比较直接、容易理解,但是考虑到以后的事情,我们将其修改为另外一种实现形式。
把上面表达式的θ换成−b,于是就可以用下式来表示感知机的行为
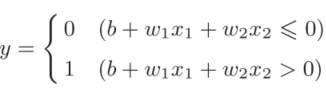
虽然有一个符号不同,但表达的内容是完全相同的。此处,b称为偏置,w1和w2称为权重。
感知机会计算输入信号和权重的乘积,然后加上偏置,如果这个值大于0则输出1,否则输出0。
下面,我们使用NumPy,按上式的方式实现感知机。
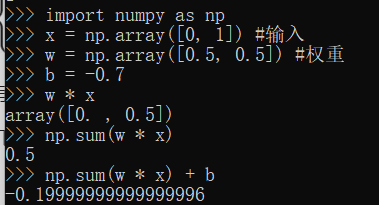
2.3.3 使用权重和偏置的实现
像下面这样实现与门
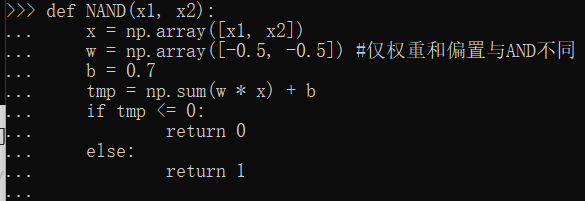
与非门
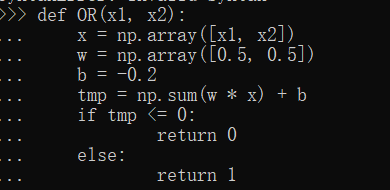
或门
2.4 感知机的局限
到这里我们已经知道,使用感知机可以实现与门、与非门、或门三种逻辑电路。现在我们来考虑一下异或门(XOR gate)。
2.4.1 异或门
异或门也被称为逻辑异或电路。
仅当x1或x2中的一方为1时,才会输出1(“异或”是拒绝其他的意思)。
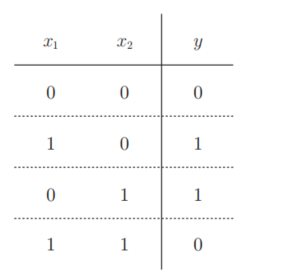
那么,要用感知机实现这个异或门的话,应该设定什么样的权重参数呢?
实际上,用前面介绍的感知机是无法实现这个异或门的。为什么用感知机可以实现与门、或门,却无法实现异或门呢?
首先,我们试着将或门的动作形象化。或门的情况下,当权重参数(b, w1, w2) = (−0.5, 1.0, 1.0)时,可满足真值表条件。此时,感知机可用下式表示。
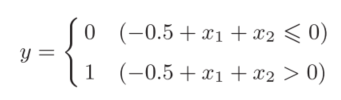
感知机会生成由直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1,另一个灰色空间输出0
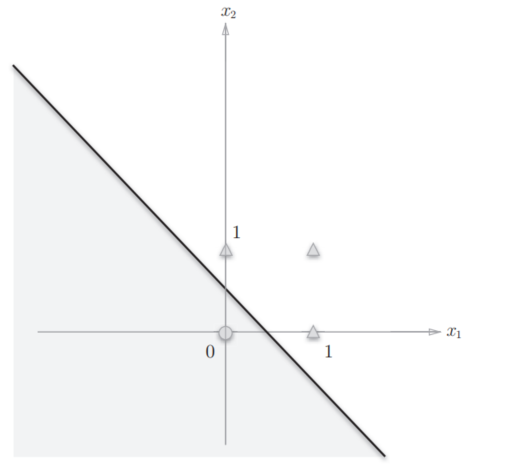
如果想制作或门,需要用直线将图中的○和△分开。实际上,刚才的那条直线就将这4个点正确地分开了。
那么,换成异或门的话会如何呢?能否像或门那样,用一条直线作出分割图中的○和△的空间呢?
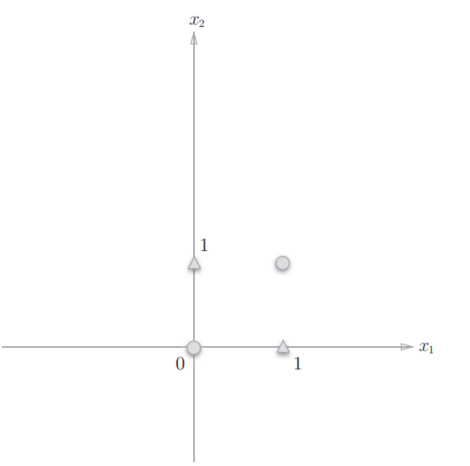
很显然,用一条直线是无法将○和△分开的。
2.4.2 线性和非线性
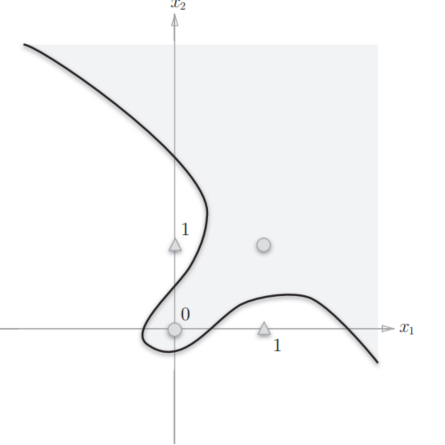
图中的○和△无法用一条直线分开,但是如果将“直线”这个限制条件去掉,就可以实现了。
感知机的局限性就在于它只能表示由一条直线分割的空间。
由曲线分割而成的空间称为非线性空间,由直线分割而成的空间称为线性空间。
2.5 多层感知机
感知机不能表示异或门让人深感遗憾,但也无需悲观。实际上,感知机的绝妙之处在于它可以“叠加层”
这里,我们暂且不考虑叠加层具体是指什么,先从其他视角来思考一下异或门的问题。
2.5.1 已有门电路的组合
异或门的制作方法有很多,其中之一就是组合我们前面做好的与门、与非门、或门进行配置
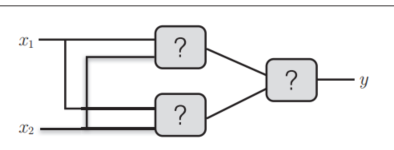
将与门、与非门、或门代入到下图的“?”中,就可以实现异或门!
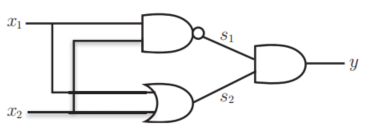
也就是这样
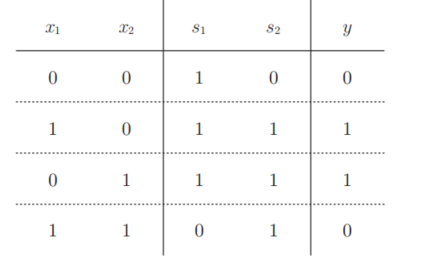
这里,把s1作为与非门的输出,把s2作为或门的输出,填入真值表中。结果如下图:
2.5.2 异或门的实现
使用之前定义的AND函数、NAND函数、OR函数,可以像下面这样(轻松地)实现

这个XOR函数会输出预期的结果。

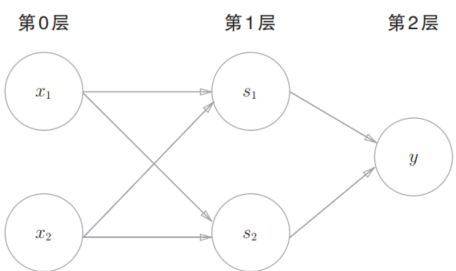
这样,异或门的实现就完成了。下面我们试着用感知机的表示方法(明确地显示神经元)来表示这个异或门。
异或门是一种多层结构的神经网络。这里,将最左边的一列称为第0层,中间的一列称为第1层,最右边的一列称为第2层。
实际上,与门、或门是单层感知机,而异或门是2层感知机。叠加了多层的感知机也称为多层感知机。
2.6 从与非门到计算机
与非门可以使用感知机实现。也就是说,如果通过组合与非门可以实现计算机的话,那么通过组合感知机也可以表示计算机(感知机的组合可以通过叠加了多层的单层感知机来表示)。
那么,什么构造的感知机才能表示计算机呢?层级多深才可以构建计算机呢?
理论上可以说2层感知机就能构建计算机。这是因为,已有研究证明,2层感知机(严格地说是激活函数使用了非线性的sigmoid函数的感知机,具体请参照下一章)可以表示任意函数。但是,使用2层感知机的构造,通过设定合适的权重来构建计算机是一件非常累人的事情。
2.7 小结
- 感知机是具有输入和输出的算法。给定一个输入后,将输出一个既定的值。
- 感知机将权重和偏置设定为参数。
- 使用感知机可以表示与门和或门等逻辑电路。
- 异或门无法通过单层感知机来表示。
- 使用2层感知机可以表示异或门。
- 单层感知机只能表示线性空间,而多层感知机可以表示非线性空间。
- 多层感知机(在理论上)可以表示计算机。
如果我的内容对你有帮助,请辛苦动动您的手指为我点赞,评论,收藏。感谢大家!!
