DAY 17 常见聚类算法-2025.8.29
常见聚类算法
知识点
- 聚类的指标
- 聚类常见算法:kmeans聚类、dbscan聚类、层次聚类
- 三种算法对应的流程
实际在论文中聚类的策略不一定是针对所有特征,可以针对其中几个可以解释的特征进行聚类,得到聚类后的类别,这样后续进行解释也更加符合逻辑。
聚类的流程
- 标准化数据
- 选择合适的算法,根据评估指标调参( )
KMeans 和层次聚类的参数是K值,选完k指标就确定
DBSCAN 的参数是 eps 和min_samples,选完他们出现k和评估指标
以及层次聚类的 linkage准则等都需要仔细调优。
除了经典的评估指标,还需要关注聚类出来每个簇对应的样本个数,避免太少没有意义。
- 将聚类后的特征添加到原数据中
- 原则t-sne或者pca进行2D或3D可视化
作业: 对心脏病数据集进行聚类。
笔记:
一、聚类的指标
聚类指标用于评估聚类结果的有效性,分为内部指标(仅用数据自身特征)和外部指标(需真实类别标签):
1. 内部指标
以下是三种常用的聚类效果评估指标,分别用于衡量聚类的质量和簇的分离与紧凑程度:
1. 轮廓系数 (Silhouette Score)
- 定义:轮廓系数衡量每个样本与其所属簇的紧密程度以及与最近其他簇的分离程度。
- 取值范围:[-1, 1]
- 轮廓系数越接近 1,表示样本与其所属簇内其他样本很近,与其他簇很远,聚类效果越好。
- 轮廓系数越接近 -1,表示样本与其所属簇内样本较远,与其他簇较近,聚类效果越差(可能被错误分类)。
- 轮廓系数接近 0,表示样本在簇边界附近,聚类效果无明显好坏。
- 使用建议:选择轮廓系数最高的
k值作为最佳簇数量。
2. CH 指数 (Calinski-Harabasz Index)
- 定义:CH 指数是簇间分散度与簇内分散度之比,用于评估簇的分离度和紧凑度。
- 取值范围:[0, +∞)
- CH 指数越大,表示簇间分离度越高,簇内紧凑度越高,聚类效果越好。
- 没有固定的上限,值越大越好。
- 使用建议:选择 CH 指数最高的
k值作为最佳簇数量。
3. DB 指数 (Davies-Bouldin Index)
- 定义:DB 指数衡量簇间距离与簇内分散度的比值,用于评估簇的分离度和紧凑度。
- 取值范围:[0, +∞)
- DB 指数越小,表示簇间分离度越高,簇内紧凑度越高,聚类效果越好。
- 没有固定的上限,值越小越好。
- 使用建议:选择 DB 指数最低的
k值作为最佳簇数量。
2. 外部指标
1. 兰德指数(Adjusted Rand Index, ARI):
- 定义: 衡量聚类结果与真实标签的吻合度
- 取值范围: [-1,1]
- 1 表示完全吻合
- 0 表示随机聚类。
- 互信息(Mutual Information, MI)及调整互信息(Adjusted Mutual Information, AMI):
- 定义:量化聚类结果与真实标签的共享信息,AMI 消除了随机因素影响。
- 取值范围 :[0,1]
- 1 表示完全一致。
二、聚类常见算法
| 算法名称 | 核心思想 | 适用场景 |
|---|---|---|
| KMeans 聚类 | 预先指定簇数 K,通过迭代最小化簇内样本的平方误差和(SSE),将样本划分到最近的簇中心 | 数据分布呈凸形、簇数已知的场景 |
| DBSCAN 聚类 | 基于密度定义 “核心点”“边界点”“噪声点”,通过邻域密度连接核心点形成簇,无需指定簇数 | 数据形状不规则、含噪声的场景 |
| 层次聚类 | 按 “自下而上聚合” 或 “自上而下拆分” 的方式,构建聚类层次树( dendrogram ) | 需展示数据层级关系、簇数不确定场景 |
1. KMeans 聚类
1. 算法原理
KMeans 是一种基于距离的聚类算法,需要预先指定聚类个数,即 k。其核心步骤如下:
- 随机选择
k个样本点作为初始质心(簇中心)。 - 计算每个样本点到各个质心的距离,将样本点分配到距离最近的质心所在的簇。
- 更新每个簇的质心为该簇内所有样本点的均值。
- 重复步骤 2 和 3,直到质心不再变化或达到最大迭代次数为止。
2. 确定簇数的方法:肘部法
- 肘部法(Elbow Method) 是一种常用的确定
k值的方法。 - 原理: 通过计算不同
k值下的簇内平方和(Within-Cluster Sum of Squares, WCSS),绘制k与 WCSS 的关系图。 - 选择标准: 在图中找到“肘部”点,即 WCSS 下降速率明显减缓的
k值,通常认为是最佳簇数。这是因为增加k值带来的收益(WCSS 减少)在该点后变得不显著。
3. KMeans 算法的优缺点
优点
- 简单高效:算法实现简单,计算速度快,适合处理大规模数据集。
- 适用性强:对球形或紧凑的簇效果较好,适用于特征空间中簇分布较为均匀的数据。
- 易于解释:聚类结果直观,簇中心具有明确的物理意义。
缺点
- 需预先指定
k值:对簇数量k的选择敏感,不合适的k会导致聚类效果较差。 - 对初始质心敏感:初始质心的随机选择可能导致结果不稳定或陷入局部最优(可通过 KMeans++ 初始化方法缓解)。
- 对噪声和异常值敏感:异常值可能会显著影响质心的位置,导致聚类结果失真。
- 不适合非球形簇:对非线性可分或形状复杂的簇效果较差,无法处理簇密度不均的情况。
2. DBSCAN 聚类
1. 算法原理
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,基于密度的带有噪声的空间聚类应用)是一种基于密度的聚类算法,无需事先知道要形成的簇类的数量,能够发现任意形状的簇,同时还能识别出数据集中的噪声点。核心步骤如下:
- 设定两个参数:邻域半径 ε(Epsilon)、邻域内最小样本数 MinPts;
- 遍历每个未标记样本,计算其 ε 邻域内的样本数:
- 若样本数≥MinPts,标记为 “核心点”,并递归寻找其密度可达的所有样本,形成一个簇;
- 若样本数 <MinPts,标记为 “边界点”(若在某核心点的 ε 邻域内)或 “噪声点”;
- 遍历所有样本后,输出所有簇及噪声点。
2. 基本概念
- 核心点(Core Point):在给定半径 ε(邻域半径)的邻域内,包含样本点的数量不小于 MinPts(邻域内最小样本数)的点。也就是说,如果点 p 的 ε- 邻域内至少有 MinPts 个样本点,那么点 p 就是核心点。例如,给定 ε = 0.5,MinPts = 5,若点 A 的 0.5 邻域内有 6 个样本点,那么点 A 就是核心点。
- 边界点(Border Point):在给定半径 ε 的邻域内,包含样本点的数量小于 MinPts,但该点落在某个核心点的 ε- 邻域内。边界点本身不是核心点,但它与核心点相关联。比如点 B 的 0.5 邻域内只有 3 个样本点,但它在核心点点 A 的 0.5 邻域内,那么点 B 就是边界点。
- 噪声点(Noise Point):既不是核心点也不是边界点的点,即不在任何核心点的 ε- 邻域内的点。
- 直接密度可达(Directly Density-Reachable):对于样本集合 D,如果 p 是核心点,q 在 p 的 ε- 邻域内,那么称点 q 从点 p 直接密度可达。例如,点 p 是核心点,点 q 在点 p 的 ε 邻域内,就可以说 q 从 p 直接密度可达 。
- 密度可达(Density-Reachable):如果存在一个点的序列 p1, p2, …, pn ,其中 p1 = p,pn = q,对于 pi ∈ D (1 <= i <= n) ,pi+1 从 pi 直接密度可达,则称点 q 从点 p 密度可达。这是一个传递关系,密度可达不具有对称性。
- 密度相连(Density-Connected):如果存在一个点 o,使得点 p 和点 q 都从点 o 密度可达,那么称点 p 和点 q 密度相连,密度相连具有对称性。
3. 算法流程
- 初始化:设定参数 ε(邻域半径)和 MinPts(邻域内最小样本数),标记所有样本点为 “未访问” 状态。
- 遍历样本点:逐个检查数据集中的每个样本点 p ,如果点 p 已经被访问过,则跳过;如果点 p 未被访问过,标记点 p 为 “已访问”,并计算点 p 的 ε- 邻域内的样本点数量。
- 判断核心点:如果点 p 的 ε- 邻域内样本点数量小于 MinPts,将点 p 标记为 “噪声点”。如果点 p 的 ε- 邻域内样本点数量大于等于 MinPts,将点 p 标记为 “核心点”,并创建一个新的簇 C ,将点 p 加入簇 C 中。
- 扩展簇:对于点 p 的 ε- 邻域内所有未访问过的样本点 q ,标记点 q 为 “已访问”,并将点 q 加入簇 C 中。如果点 q 是核心点,递归地处理点 q 的 ε- 邻域内的所有未访问过的样本点,将它们也加入到簇 C 中。
- 重复操作:重复步骤 2 - 4,直到所有的样本点都被访问过。此时,生成的各个簇就是 DBSCAN 聚类的结果,而那些没有被划分到任何簇中的 “噪声点”,就作为数据集中的异常或不相关数据被识别出来。
4. DBSCAN 聚类的优缺点
优点
- 无需事先知道簇的数量:相比 K-Means 等算法,不需要提前指定要聚类的簇数,算法会根据数据的密度自动确定。
- 能够发现任意形状的簇:可以有效识别出非球形(如环形、链状等不规则形状)的簇,而 K-Means 等基于距离中心的算法往往只能发现球形的簇。
- 能识别噪声点:可以将不在任何簇中的点标记为噪声点,能够很好地处理数据集中存在的噪声数据。
缺点
- 对参数敏感:参数 ε 和 MinPts 的选择对聚类结果影响很大。不同的参数设置可能会得到完全不同的聚类结果,而且在实际应用中,很难事先确定这两个参数的最优值。
- 计算复杂度高:在高维数据和大规模数据集上,计算每个点的 ε- 邻域内的样本点数量的计算量较大,导致算法的时间复杂度较高。
- 不能很好地反映高维数据的密度差异:在高维空间中,数据分布变得稀疏,传统基于距离定义的密度概念可能不再适用,导致聚类效果不佳。
3. 层次聚类
1. 算法原理
层次聚类(Hierarchical Clustering)是一种通过构建层次化的簇结构来实现数据聚类的算法,无需预先指定簇的数量,最终可形成类似 “树状图”(Dendrogram)的聚类结果,核心是通过 “合并” 或 “拆分” 簇完成层次构建。核心流程如下:
- 初始时,每个样本单独作为一个簇,共 N 个簇;
- 计算所有簇之间的相似度(或距离,如欧氏距离、曼哈顿距离);
- 合并相似度最高(或距离最近)的两个簇,形成新簇,此时簇数减少 1;
- 重复步骤 2-3,直到所有样本合并为一个簇;
- 根据聚类层次树(dendrogram),选择合适的截断位置,确定最终簇数及聚类结果。
2. 核心分类:两种基本策略
层次聚类根据簇的构建方向,分为凝聚式(自底向上) 和分裂式(自顶向下) 两类,其中凝聚式层次聚类因实现简单、应用广泛,是主流方式。
| 类型 | 核心逻辑 | 特点 |
|---|---|---|
| 凝聚式(Agglomerative) | 初始时每个样本为独立簇 → 反复合并 “最相似” 的两个簇 → 最终合并为 1 个簇 | 从细到粗,计算量相对较小,应用最广 |
| 分裂式(Divisive) | 初始时所有样本为 1 个簇 → 反复拆分 “最不相似” 的簇 → 最终拆分为单个样本 | 从粗到细,计算量较大,适用于小数据集 |
3. 关键概念:簇相似度的度量(距离 / 链接方式)
层次聚类的核心是定义 “两个簇之间的相似度”,常用 “距离” 衡量(距离越小,相似度越高),主流 “链接方式”(Linkage)有 4 种:
| 链接方式 | 计算逻辑(衡量簇 A 和簇 B 的距离) | 适用场景 |
|---|---|---|
| 单链接(Single Linkage) | 簇 A 中所有点与簇 B 中所有点的最小距离 | 适合发现细长型簇,但对噪声敏感 |
| 全链接(Complete Linkage) | 簇 A 中所有点与簇 B 中所有点的最大距离 | 簇内密度更均匀,避免异常值影响 |
| 平均链接(Average Linkage) | 簇 A 中所有点与簇 B 中所有点的平均距离 | 平衡单链接和全链接,应用较广 |
| 质心链接(Centroid Linkage) | 簇 A 的质心(均值点)与簇 B 的质心的距离 | 计算简单,但可能出现 “逆合并”(簇合并后距离反而变小) |
4. 主流流程:凝聚式层次聚类(以欧式距离 + 平均链接为例)
- 初始化:将数据集中的每个样本点视为一个独立的 “初始簇”,假设共 N 个样本,初始簇数量为 N。
- 计算距离矩阵:计算所有两两簇(此时为单个样本)之间的距离(如欧式距离),形成 N×N 的距离矩阵。
- 合并最相似簇:在距离矩阵中找到 “距离最小” 的两个簇,将它们合并为一个新簇,此时簇总数减少 1(变为 N-1)。
- 更新距离矩阵:重新计算 “新簇” 与其他所有剩余簇之间的距离(按选定的链接方式,如平均链接计算新簇与其他簇的平均距离),更新距离矩阵。
- 重复合并与更新:重复步骤 3-4,每次合并距离最小的两个簇并更新距离矩阵,直到所有样本最终合并为 1 个簇。
- 生成结果:通过 “树状图(Dendrogram)” 展示层次化簇结构,可根据需求在树状图的某一层 “切割”,得到最终的 K 个簇(K 由业务或树状图密度确定)。
5. 层次聚类优缺点
| 优点 | 缺点 |
|---|---|
| 1.无需预先指定簇数量,结果直观(树状图可解释); 2.能发现任意形状的簇; 3.实现逻辑简单,易理解。 | 1. 时间复杂度高(O (N³),N 为样本数),不适合大规模数据; 2.一旦合并 / 拆分簇,无法回溯调整,对初始距离敏感; 3.高维数据中距离度量的区分度下降,聚类效果变差。 |
作业 : 对心脏病数据集进行聚类
# 数据导入
import pandas as pd
data = pd.read_csv('heart.csv')
data.head()
age sex cp trestbps chol fbs restecg thalach exang oldpeak slope ca thal target
0 63 1 3 145 233 1 0 150 0 2.3 0 0 1 1
1 37 1 2 130 250 0 1 187 0 3.5 0 0 2 1
2 41 0 1 130 204 0 0 172 0 1.4 2 0 2 1
3 56 1 1 120 236 0 1 178 0 0.8 2 0 2 1
4 57 0 0 120 354 0 1 163 1 0.6 2 0 2 1# 区分标签和特征
X = data.drop(['target'],axis=1)
y = data['target']# 对特征做数据标准化处理
from sklearn.preprocessing import StandardScaler # 包导入
scaler = StandardScaler() # 初始化
X_scaled = scaler.fit_transform(X) # 对X做标准化
1. Kmeans 聚类分析
from sklearn.cluster import KMeans # 导入K-meand聚类算法
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score # 导入轮廓系数,CH指数,DB指数# 评估不同K值下的指标
k_range = range(2,11) # 选择范围 K 从 2 到 10
inertia_values = [] # 存储不同k值对应的惯性(肘部法则)
silhouette_scores = [] # 存储不同k值对应的轮廓系数
ch_scores = [] # 存储不同k值对应的CH指数
db_scores = [] # 存储不同k值对应的DB指数# 利用for循环遍历所有K值,计算不同K值的惯性,轮廓系数,CH指数,DB指数,并存储for k in k_range:kmeans = KMeans(k,random_state=42) # 初始化KMeans模型,指定聚类数为k,设置随机种子确保结果可重现kmeans_labels = kmeans.fit_predict(X_scaled) # 对标准化后的数据集X_scaled进行拟合并预测聚类标签inertia_value = kmeans.inertia_ # 计算惯性(所有样本到其最近聚类中心的距离平方和)inertia_values.append(inertia_value) # 存储silhouette = silhouette_score(X_scaled,kmeans_labels) # 计算轮廓系数(评估聚类质量,范围[-1,1],越接近1越好)silhouette_scores.append(silhouette) # 存储ch = calinski_harabasz_score(X_scaled,kmeans_labels) # 计算CH指数(值越大表示聚类效果越好)ch_scores.append(ch) # 存储db = davies_bouldin_score(X_scaled,kmeans_labels) # 计算DB指数(值越小表示聚类效果越好)db_scores.append(db) # 存储print(f'k={k},惯性:{inertia_value:.2f},轮廓系数:{silhouette:.3f},CH 指数:{ch:.2f}, DB 指数:{db:.3f}')# 绘制评估指标图
plt.figure(figsize=(15,10)) # 新建画布# 肘部法则图(Inertia)
plt.subplot(2,2,1) # 包含2行 2列的子图,当前为第一个子图
plt.plot(k_range,inertia_values,marker = 'o') # x值为k_range,y值为inertia_values
plt.title('肘部法则确定最优聚类数k(惯性越小越好)') # 标题
plt.xlabel('聚类数(k)') # 横坐标
plt.ylabel('惯性') # 纵坐标
plt.grid(True) # 显示网格# 轮廓系数图
plt.subplot(2,2,2) # 当前为第二个子图
plt.plot(k_range,silhouette_scores,marker='o', color='orange') # x值为k_range,y值为silhouette_scores
plt.title('轮廓系数确定最优聚类数k(越大越好)') # 标题
plt.xlabel('聚类数(k)') # 横坐标
plt.ylabel('轮廓系数') # 纵坐标
plt.grid(True) # 显示网格# CH指数图
plt.subplot(2,2,3) # 当前为第三个子图
plt.plot(k_range,ch_scores,marker='o',color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数k(越大越好)')
plt.xlabel('聚类数(k)')
plt.ylabel('CH指数')
plt.grid(True)# DB 指数图
plt.subplot(2,2,4) # 当前为第四个子图
plt.plot(k_range,db_scores,marker = 'o',color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k(越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()
k=2,惯性:3331.64,轮廓系数:0.166,CH 指数:54.87, DB 指数:2.209
k=3,惯性:3087.69,轮廓系数:0.112,CH 指数:41.36, DB 指数:2.544
k=4,惯性:2892.52,轮廓系数:0.118,CH 指数:36.06, DB 指数:2.175
k=5,惯性:2814.65,轮廓系数:0.094,CH 指数:29.76, DB 指数:2.386
k=6,惯性:2673.22,轮廓系数:0.095,CH 指数:28.13, DB 指数:2.377
k=7,惯性:2596.68,轮廓系数:0.088,CH 指数:25.50, DB 指数:2.290
k=8,惯性:2464.39,轮廓系数:0.115,CH 指数:25.22, DB 指数:2.136
k=9,惯性:2415.63,轮廓系数:0.105,CH 指数:23.18, DB 指数:2.133
k=10,惯性:2337.41,轮廓系数:0.111,CH 指数:22.31, DB 指数:2.056
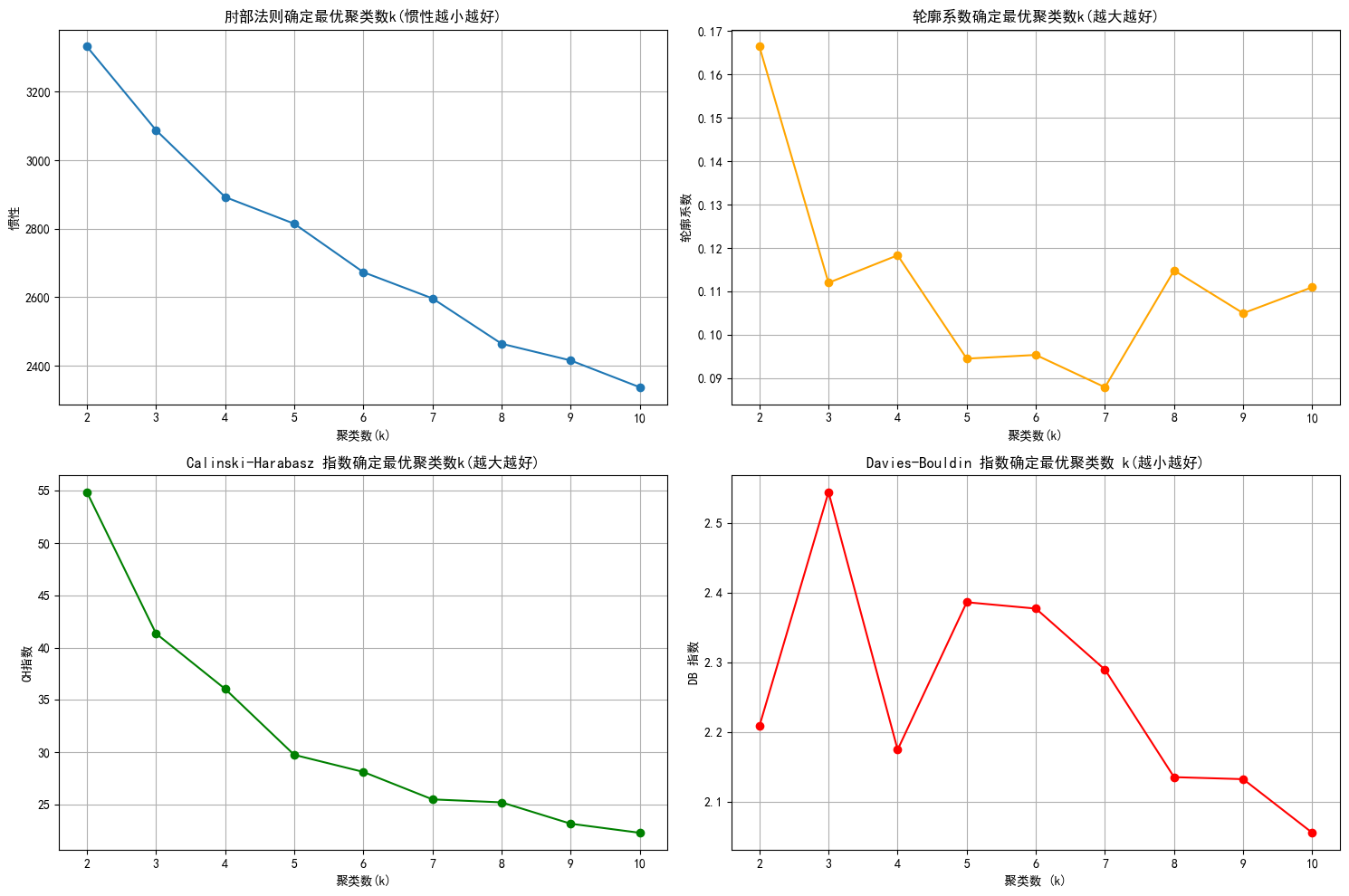
- 根据肘部法则,都可以
- 根据轮廓系数,2,4,8,10
- 根据CH指数,8之前
- 根据DB指数,2,4,10
综上,2,4应该都可以,我们选择4
selected_k = 4# 使用选择的 k 值进行 KMeans 聚类
kmeans = KMeans(n_clusters=selected_k,random_state=42)
kmeans_labels = kmeans.fit_predict(X_scaled)
X['KMeans_Cluster'] = kmeans_labels # 在原始数据集 X 中添加一列 "KMeans_Cluster",存储每个样本对应的聚类标签,便于后续分析# 导入pca
from sklearn.decomposition import PCA # 使用pca降维到 2D 进行可视化
pca = PCA(n_components=2) #初始化 PCA(主成分分析)模型,指定降维到 2 个维度
X_pca = pca.fit_transform(X_scaled) #对标准化数据 X_scaled 进行 PCA 降维处理import matplotlib.pyplot as plt
import seaborn as sns # 导入seaborn# KMeans 聚类结果可视化
plt.figure(figsize=(6,5)) # 建画布
sns.scatterplot(x=X_pca[:,0],y=X_pca[:,1],hue = kmeans_labels,palette='viridis')
# 使用 seaborn 绘制散点图,x 轴为 PCA 第一主成分,y 轴为 PCA 第二主成分
# 用不同颜色(hue=kmeans_labels)表示不同的聚类
# 使用 'viridis' 调色板,使颜色区分明显plt.title(f'KMeans Clustering with k={selected_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 KMeans 聚类标签的前几行
print(f"KMeans Cluster labels (k={selected_k}) added to X:")
print(X[['KMeans_Cluster']].value_counts())
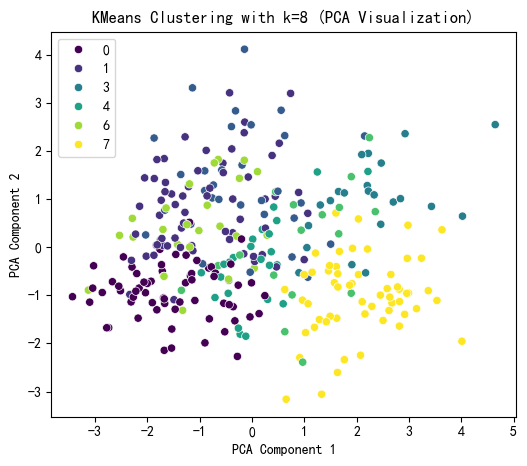
KMeans Cluster labels (k=8) added to X:
KMeans_Cluster
0 64
1 63
7 57
2 31
6 25
4 24
3 22
5 17
Name: count, dtype: int64
2. DBSCAN聚类
import numpy as np
import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 eps 和 min_samples 下的指标
# eps这个参数表示邻域的半径,min_samples表示一个点被认为是核心点所需的最小样本数。
# min_samples这个参数表示一个核心点所需的最小样本数。eps_range = np.arange(0.3, 0.8, 0.1) # 测试 eps 从 0.3 到 0.7
min_samples_range = range(3, 8) # 测试 min_samples 从 3 到 7
results = []for eps in eps_range:for min_samples in min_samples_range:dbscan = DBSCAN(eps=eps, min_samples=min_samples)dbscan_labels = dbscan.fit_predict(X_scaled)# 计算簇的数量(排除噪声点 -1)n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)# 计算噪声点数量n_noise = list(dbscan_labels).count(-1)# 只有当簇数量大于 1 且有有效簇时才计算评估指标if n_clusters > 1:# 排除噪声点后计算评估指标mask = dbscan_labels != -1if mask.sum() > 0: # 确保有非噪声点silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask])ch = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask])db = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask])results.append({'eps': eps,'min_samples': min_samples,'n_clusters': n_clusters,'n_noise': n_noise,'silhouette': silhouette,'ch_score': ch,'db_score': db})print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")else:print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)
eps=0.3, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
算法应该不合适,没有继续做
3. 层次聚类
import numpy as np
import pandas as pd
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 n_clusters 下的指标
n_clusters_range = range(2, 11) # 测试簇数量从 2 到 10
silhouette_scores = []
ch_scores = []
db_scores = []for n_clusters in n_clusters_range:agglo = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward') # 使用 Ward 准则合并簇agglo_labels = agglo.fit_predict(X_scaled)# 计算评估指标silhouette = silhouette_score(X_scaled, agglo_labels)ch = calinski_harabasz_score(X_scaled, agglo_labels)db = davies_bouldin_score(X_scaled, agglo_labels)# 存储评估指标silhouette_scores.append(silhouette)ch_scores.append(ch)db_scores.append(db)# 打印结果print(f"n_clusters={n_clusters}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 5))# 轮廓系数图
plt.subplot(1, 3, 1) # 1 行 3 列的子图,当前为第一个子图
plt.plot(n_clusters_range, silhouette_scores, marker='o')
plt.title('轮廓系数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(1, 3, 2) # 1 行 3 列的子图,当前为第二个子图
plt.plot(n_clusters_range, ch_scores, marker='o')
plt.title('Calinski-Harabasz 指数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(1, 3, 3) # 1 行 3 列的子图,当前为第三个子图
plt.plot(n_clusters_range, db_scores, marker='o')
plt.title('Davies-Bouldin 指数确定最优簇数(越小越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()
n_clusters=2, 轮廓系数: 0.133, CH 指数: 38.71, DB 指数: 2.564
n_clusters=3, 轮廓系数: 0.097, CH 指数: 32.44, DB 指数: 2.558
n_clusters=4, 轮廓系数: 0.104, CH 指数: 31.10, DB 指数: 2.194
n_clusters=5, 轮廓系数: 0.104, CH 指数: 27.60, DB 指数: 2.567
n_clusters=6, 轮廓系数: 0.113, CH 指数: 25.59, DB 指数: 2.265
n_clusters=7, 轮廓系数: 0.097, CH 指数: 23.90, DB 指数: 2.230
n_clusters=8, 轮廓系数: 0.100, CH 指数: 22.85, DB 指数: 2.281
n_clusters=9, 轮廓系数: 0.107, CH 指数: 21.78, DB 指数: 2.195
n_clusters=10, 轮廓系数: 0.111, CH 指数: 20.81, DB 指数: 2.120
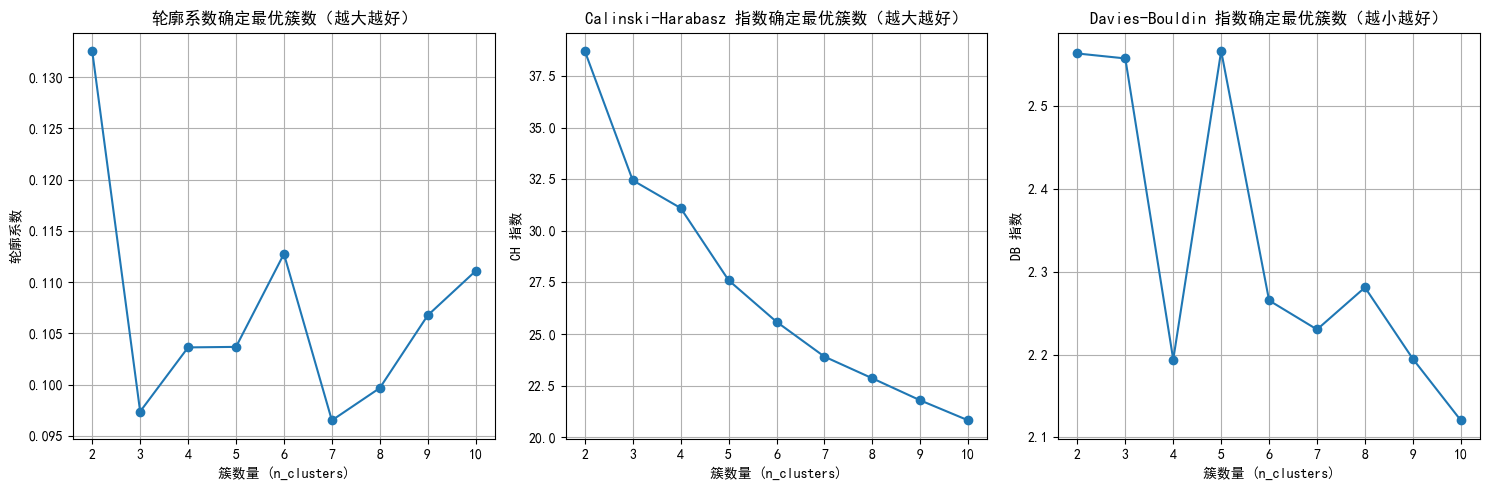
- 从轮廓系数来看,2,6,10
- 从DB指数来看,4,7,10
这里我选择了10
# 提示用户选择 n_clusters 值(这里可以根据图表选择最佳簇数)
selected_n_clusters = 10 # 示例值,根据图表调整# 使用选择的簇数进行 Agglomerative Clustering 聚类
agglo = AgglomerativeClustering(n_clusters=selected_n_clusters, linkage='ward')
agglo_labels = agglo.fit_predict(X_scaled)
X['Agglo_Cluster'] = agglo_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# Agglomerative Clustering 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=agglo_labels, palette='viridis')
plt.title(f'Agglomerative Clustering with n_clusters={selected_n_clusters} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 Agglomerative Clustering 聚类标签的分布
print(f"Agglomerative Cluster labels (n_clusters={selected_n_clusters}) added to X:")
print(X[['Agglo_Cluster']].value_counts())
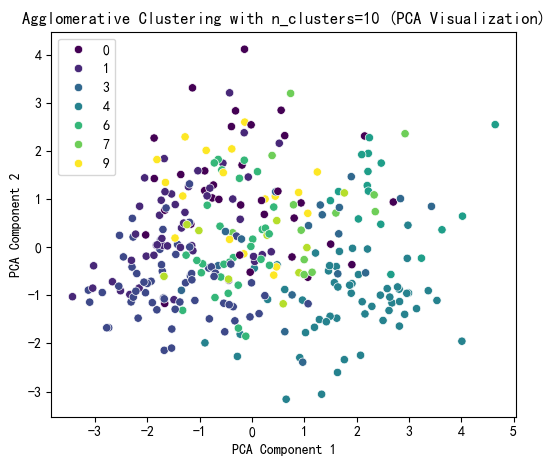
Agglomerative Cluster labels (n_clusters=10) added to X:
Agglo_Cluster
2 62
4 55
1 47
0 34
6 30
3 18
9 18
5 16
7 12
8 11
Name: count, dtype: int64
# 层次聚类的树状图可视化
from scipy.cluster import hierarchy
import matplotlib.pyplot as plt# 假设 X_scaled 是标准化后的数据
# 计算层次聚类的链接矩阵
Z = hierarchy.linkage(X_scaled, method='ward') # 'ward' 是常用的合并准则# 绘制树状图
plt.figure(figsize=(10, 6))
hierarchy.dendrogram(Z, truncate_mode='level',p=3) # p 控制显示的层次深度
# hierarchy.dendrogram(Z, truncate_mode='level') # 不用p这个参数,可以显示全部的深度
plt.title('Dendrogram for Agglomerative Clustering')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.show()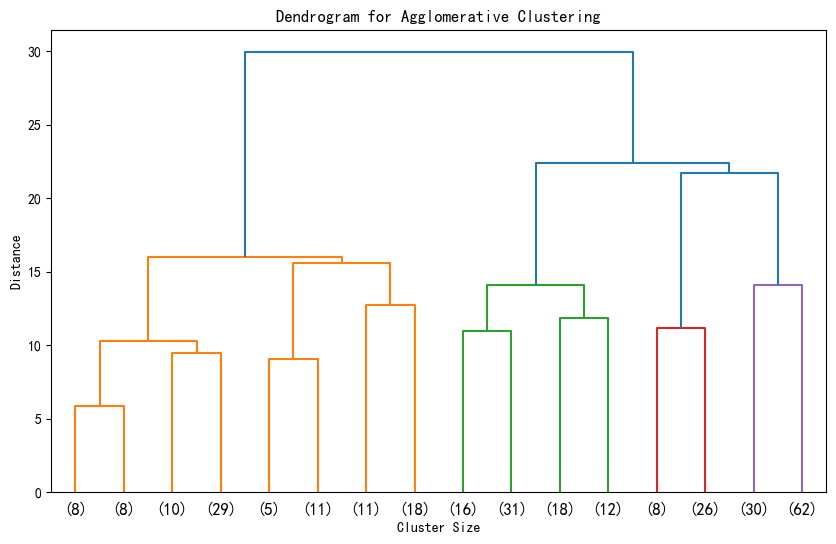
@浙大疏锦行
