学习数据结构（13）二叉树链式结构下

1.实现链式结构二叉树

（1）求二叉树节点个数

（2）求二叉树叶子节点个数

（3）求二叉树第K层节点个数

（4）求二叉树的深度/高度

（5）二叉树查找值为x的节点

（6）二叉树的销毁

（7）层序遍历

层序遍历即自上而下，自左而右逐层访问树的节点的过程，层序遍历需要额外借助队列这种数据结构来实现。

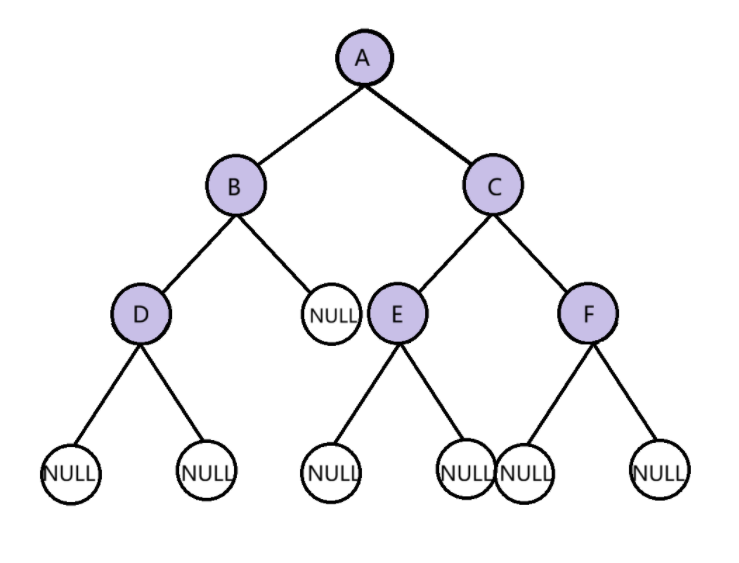
以上图所示的二叉树为例，利用队列实现层序遍历的过程如下：

将队列有关函数的头文件和源文件导入当前项目，将队列节点数据结构中数据的数据类型改为链式二叉树节点的指针，首先将根节点入队：

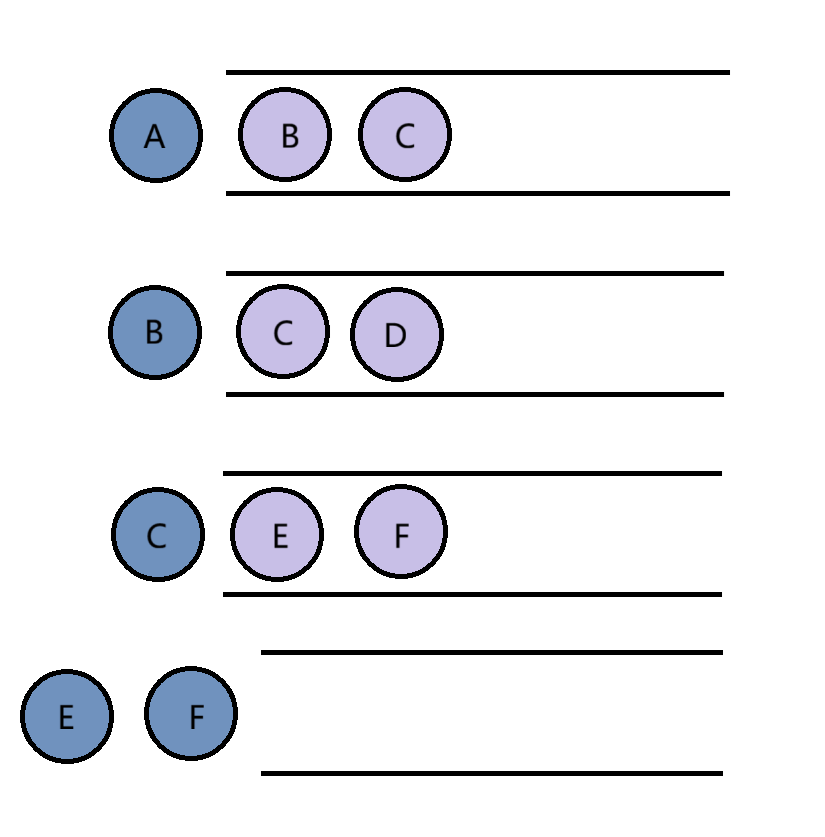
循环判断队列是否为空，若不为空，则提取队头数据，将队头出队列，若队头左右节点不为空，将队头的左右节点依次入队：

最后销毁队列

（8）判断二叉树是否为完全二叉树

创建队列，将根节点入队，循环判断队列是否为空，若不为空则提取队头数据，将队头出队，若队头数据为空指针，则跳出循环，否则将队头左右节点依次入队。

循环判断队列是否为空，若不为空则提取队头数据，将队头出队，若队头数据不为空指针，则二叉树为非完全二叉树，销毁队列，返回false，若直到跳出循环队头数据一直为空指针，则二叉树为完全二叉树，销毁队列，返回true。

2.二叉树相关选择题

（1）二叉树性质

对于任何一颗二叉树，如果度为0的叶子节点的个数为，度为2的分支节点的个数为，则有

推导：二叉树的边数既为又为，联立即可得

例题：

①在具有2n个结点的完全二叉树中，叶子结点（A）

A、n

B、n+1

C、n-1

D、n/2

解析：,,故,又在完全二叉树中，度为1的节点只可能没有或只有一个，当时，，不为整数，排除；当时，,符合题意，故选A

②一棵完全二叉树的结点数为531个，那么这棵树的高度为（B）

A、11

B、10

C、8

D、12

解析：设k为层高，满二叉树总节点个数为，当k=9时，,故这棵树高度为9+1=10，选B

（2）二叉树遍历

若给出二叉树的前序序列，则序列中第一个即二叉树的根节点，若给出二叉树的中序序列，则根节点左右两侧的序列分别是根节点的左子树和右子树，若给出二叉树的后序序列，则序列中最后一个即二叉树的根节点

例题：

③设一颗二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历（D）

A、adbce

B、decab

C、debac

D、abcde

解析：后序遍历中最后一个节点为a，故根节点为a，则由中序遍历得b为a节点的左子树，dce为a节点的右子树，依此类推，可画出二叉树的草图：

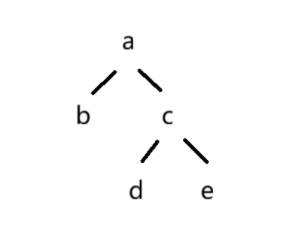，故前序序列为abcde

④某二叉树的后序遍历序列与中序遍历序列相同，均为ABCDEF，则按层次输出（同一层从左到右）的序列为（A）

A、FEDCBA

B、CBAFED

C、DEFCBA

D、ABCDEF

解析：跟上一题的分析方法相同，画出草图：

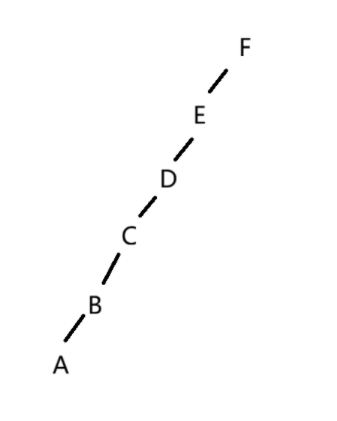，故层序序列为FEDCBA