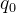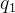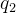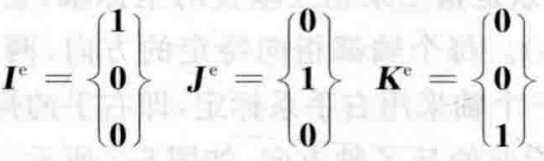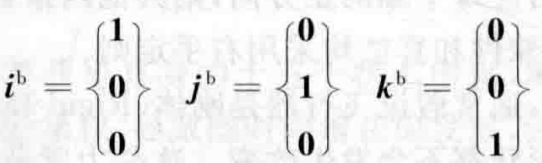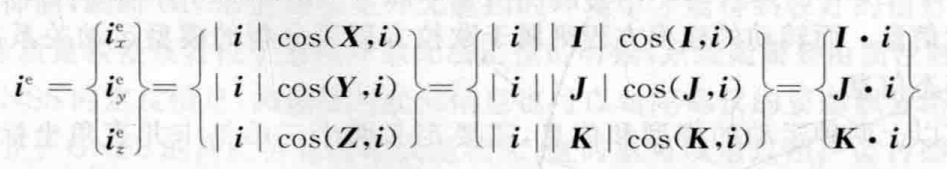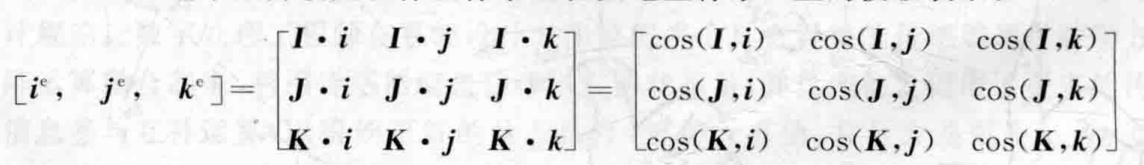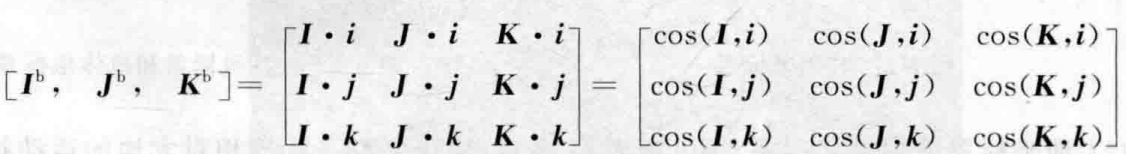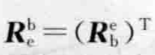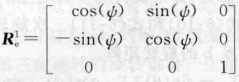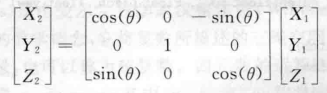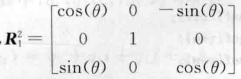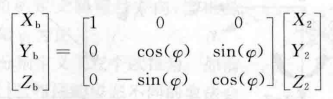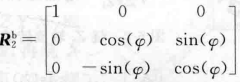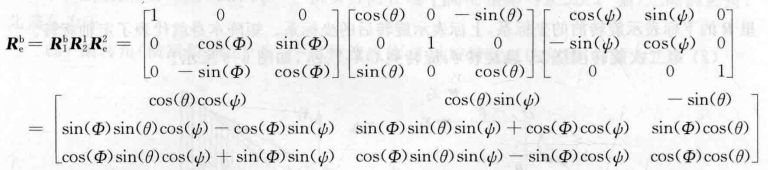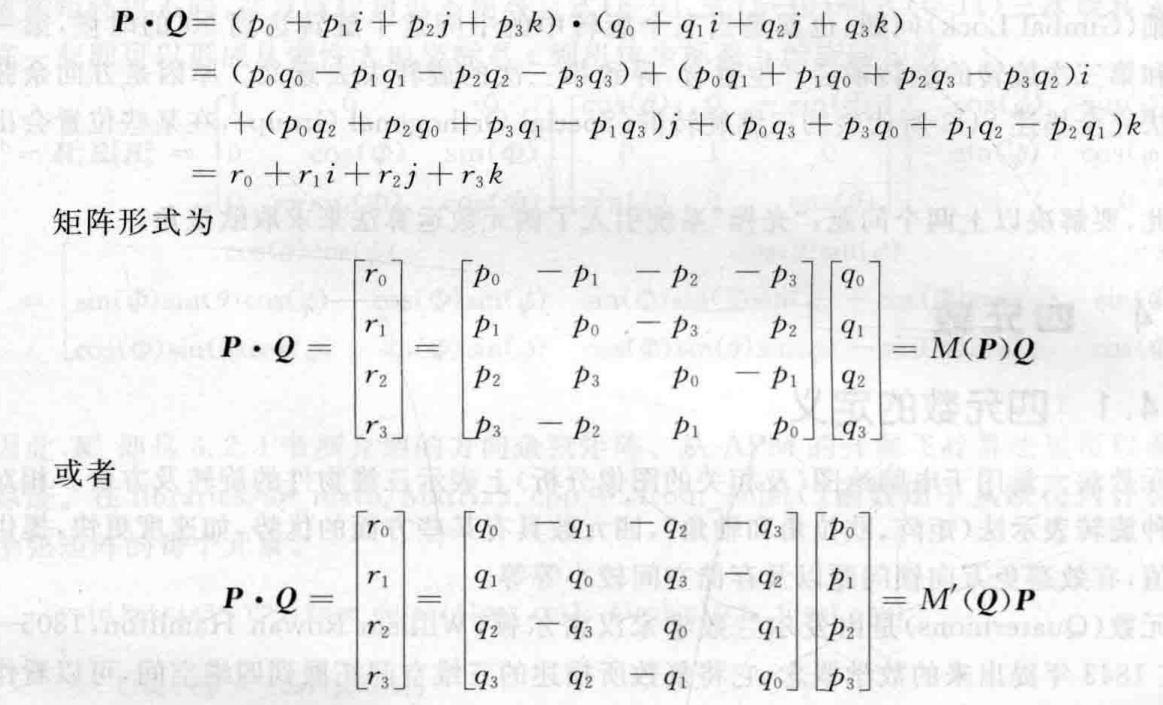当前位置：首页 > news >正文

机器人 - 无人机基础(6) - 状态估计(ing)

news 2025/8/27 15:36:15

一、组合导航

1.1 状态估计是什么

二、飞行器的坐标系

2.1 三维笛卡尔直角坐标系

三、方向余弦矩阵和欧拉角

3.1 方向余弦矩阵

一、组合导航

1.1 状态估计是什么

首先，飞行器要获取状态信息，但是通过单独的传感器容易造成误差累积；组合导航结合GNSS、惯性测量元件、磁力计、气压计、超声波等设备进行多传感器融合，得到较为准确的状态空间量，这个过程成为状态估计；

二、飞行器的坐标系

2.1 三维笛卡尔直角坐标系

指的是三条相互垂直的坐标轴，相交形成的坐标系，交点成为原点O，每个坐标轴指向特定方向；
两个不同坐标轴决定的面成为笛卡尔平面；

我们主要需要研究飞行器<位置、速度> 以及 <姿态>；

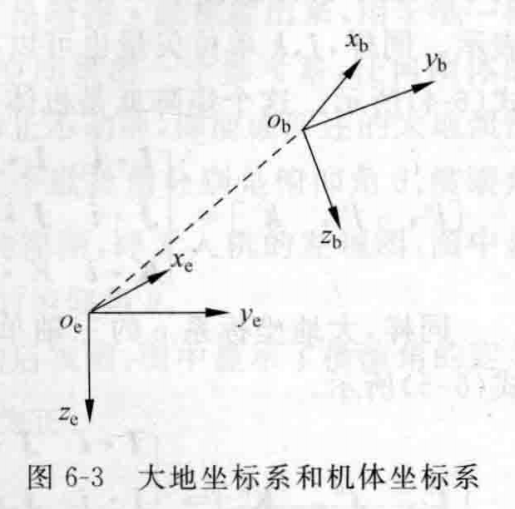
(1).大地坐标系用e或者G表示，一般把起飞点当原点，X-Y-Z方向为北-东-地，用于研究飞行器相对于大地的运动状态、空间位置坐标；
(2).机体坐标系用b或者B表示，坐标原点为机体重心，X-Y-Z方向为机身前-右-下，用于研究飞行器相对于重心的旋转运动；

三、方向余弦矩阵和欧拉角

3.1 方向余弦矩阵

对于大地坐标系e，有：

对于机体坐标系b，有：

我们这里可以把机体坐标系的三个轴的单位矢量在大地坐标系中表示，用的方法是把每个矢量投影到大地坐标系上去，比如这里把机体坐标系中的x轴的单位矢量i，投到大地坐标系上面去的话，表示为如下：
我们可以认为就是把机体坐标系中的x的单位向量，投影到大地坐标系的每个坐标轴上面去；

然后我们可以按照上述方式，把机体坐标轴中的 Y与Z 轴的单位向量 j 和 k 也投影到大地坐标系上面去，就会形成下列矩阵；

反过来，大地坐标系也可以投到机体坐标系上面去(大地坐标系的矢量用机体坐标系表示)；

方向余弦矩阵的作用：坐标间矢量的“翻译器”
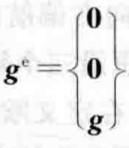
比如在大地中，重力矢量为

假如想知道，它在机体坐标系b中的投影(加速度计测得的重力分量)，那么可以

反之

矩阵的正交性：
方向余弦矩阵是正交矩阵，所以满足以下两个特性，
(1).互逆关系

(2).单位性：矩阵各行各列都是单位矢量，并且两两正交(点积为0)；

我们了解这些什么用？
比如重力矢量这里，无人机悬停的时候，机体坐标系的加速度计测得矢量 $g^b$ ，我们可以通过方向余弦矩阵(DCM)转换为大力坐标系的重力参考，来判断无人机自身姿态；

3.2 姿态与欧拉角

3.2.1 欧拉角简单介绍

三个欧拉角：
俯仰角 $\theta$

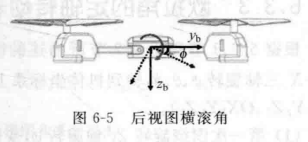
横滚角 $\phi$

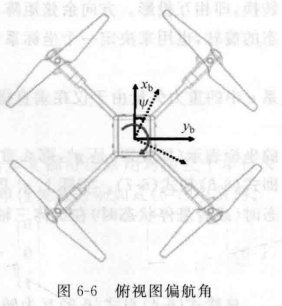
偏航角 $\psi$

相同姿态，不同取法会得到不同欧拉角，
这里用的顺序是Z-Y-X，就是先绕Z轴，再Y，最后X的旋转，达到最终姿态；
其中：

俯仰角 $\theta$ (Pitch)抬头为正，
偏航角 $\psi$ (Yaw) 正北为x轴，机头与x轴偏东为正；
横滚角 $\phi$ (Roll) 绕x轴转，右滚为正；
注意：这里x轴指向北，y指向东，z指向地；

3.2.2 欧拉角定轴转动表示矩阵

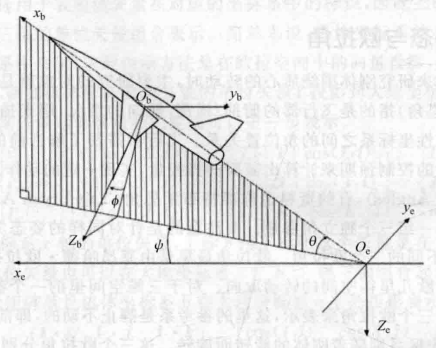
这里主要是尝试按上面说的按Z-Y-X旋转，从大地坐标系e，转换到机体坐标系b

(1).围绕Z轴旋转：

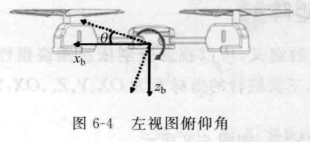
这个比较好理解，可以看右边那个平面视图，Z轴这里是朝着我们，所以看不见，把e坐标系绕着Z轴，旋转 $\psi$ 得到1坐标系；

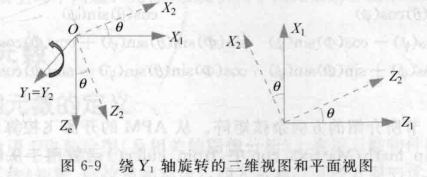
(2).围绕Y轴旋转：
与上面同理，这时候绕Y轴旋转，并且Y轴是指向我们的；

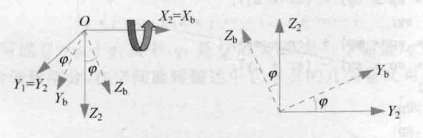
(3).围绕X轴旋转：

然后取得大地坐标系e 到机体坐标系b 的旋转矩阵：

这里右下e和右上b，是指 e坐标系转换到 b坐标系，或者说e指向b；

这里我们可以看到，当 $\theta$ =90°的时候，会出现除数为0的奇点，在物理空间称为万向节死锁问题；这里需要引入四元数运算法来求欧拉角；

3.3 四元数

3.3.1 四元数定义

四元数包含四个元素 $q_0$ $q_1$ $q_2$ $q_3$

$Q(q_0,q_1,q_2,q_3)=q_0+q_1i+q_2j+q_3k=q_0+q$

$i^2=j^2=k^2=-1$

$ij=k,jk=i,ki=j$

$ji=-k,kj=-i,ik=-j$