leetcode-hot-100 (二分查找）

1、搜索插入位置

题目链接：搜索插入位置
题目描述：
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

解答

下面的代码虽然不是很标准，但是可以通过这道题目：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;while (left < right) {int mid = (left + right) >> 1;// int mid = (left - right) >> 1 + left;if (nums[mid] == target)return mid;else if (nums[mid] > target) {right = mid - 1;} else {left = mid + 1;}}return nums[left] < target ? left + 1 : left;}
};

下面的代码才是标准的写法，也比较的安全：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {if (nums.empty())return 0;int left = 0;int right = nums.size(); // 开区间while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else {right = mid;  // 一直保持右边是开区间}}return left;}
};

2、搜索二维矩阵

题目链接：搜索二维矩阵
题目描述：
给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

解答

方法一：借助一维数组

对于二维数组的二分查找，要是不是很会的话，可以将二维数组中的元素按顺序依次存储到一维数组当中，然后再在一维数组上面实行二分查找即可。于是依据这个 取巧 思路，代码编写如下：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int row = matrix.size();int col = matrix[0].size();// 将二维数组中的元素按顺序展平到一维数组中去vector<int> temp;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {temp.push_back(matrix[i][j]);}}// 对展平后的一维数组实行二分查找即可 [left , right);int left = 0;int right = row * col;// also you can use// int right = temp.size();while (left < right) {int mid = left + (right - left) / 2;if (temp[mid] == target) {return true;} else if (temp[mid] > target) {right = mid;} else {left = mid + 1;}}return false;}
};

方法二：直接在二维矩阵上二分

无需展平数组，可以将二维矩阵看做一维数组，然后使用 坐标映射 即可。

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int row = matrix.size();int col = matrix[0].size();int left = 0;int right = row * col - 1;while (left <= right) {int mid = left + (right - left) / 2;int mid_val = matrix[mid / col][mid % col];if (mid_val == target)return true;else if (mid_val > target) {right = mid - 1;} else {left = mid + 1;}}return false;}
};

或者想使用左闭右开区间的话 $[left,right)$ ， 代码可以修改如下：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int row = matrix.size();int col = matrix[0].size();int left = 0;int right = row * col;while (left < right) {int mid = left + (right - left) / 2;int mid_val = matrix[mid / col][mid % col];if (mid_val == target)return true;else if (mid_val > target) {right = mid;} else {left = mid + 1;}}return false;}
};

方法三：灵神解法

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int row = matrix.size();int col = matrix[0].size();int i = 0;int j = col - 1;while (i < row && j >= 0) {if (matrix[i][j] == target)return true;else if (matrix[i][j] < target)i++;elsej--;}return false;}
};

3、在排序数组中查找元素的第一个和最后一个位置

题目链接：在排序数组中查找元素的第一个和最后一个位置
题目描述：
给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

解答

先分析一下题目

先不考虑时间复杂度的要求，而是先想一下这道题目有哪些解法。
首先的一个想法就是使用两个指针，对于满足条件的区间，一个指向左侧，一个指向右侧。
这样代码就编写如下：

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int len = nums.size();int left = -1;int right = -1;for (int i = 0; i < len; i++) {if (nums[i] == target) {left = i;break;}}if (left == -1)return {-1, -1};for (int i = left; i < len; i++) {if (nums[i] != target) {right = i - 1;break;}if (i == len - 1) {right = i;break;}}return {left, right};}
};

上述代码其实还有改进的地方，上面的代码不管是 left 还是 right 都是从左到右的，这样就需要考虑一下边界条件，那么实际上 right 是可以从右到左的，这样条件就可以少判断点。

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int len = nums.size();int left = -1;int right = -1;for (int i = 0; i < len; i++) {if (nums[i] == target) {left = i;break;}}if (left == -1)return {-1, -1};for (int j = len - 1; j >= left; j--) {if (nums[j] == target) {right = j;break;}}return {left, right};}
};

方法：官方解答

class Solution {
public:int binarySearch(vector<int>& nums, int target, bool lower) {int left = 0;int right = (int)nums.size() - 1;int ans = (int)nums.size();while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target || (lower && nums[mid] >= target)) {right = mid - 1;ans = mid;} else {left = mid + 1;}}return ans;}vector<int> searchRange(vector<int>& nums, int target) {int left_index = binarySearch(nums, target, true);int right_index = binarySearch(nums, target, false) - 1;if (left_index <= right_index && right_index < nums.size() &&nums[left_index] == target && nums[right_index] == target) {return vector<int>{left_index, right_index};}return vector<int>{-1, -1};}
};

4、搜索旋转排序数组

题目链接：搜索旋转排序数组
题目描述：
整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 向左旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 下标 3 上向左旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

解答

leetcode 评论区中有一种思想，我觉得不错：

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。
就这样循环即可

于是代码编写如下：

class Solution {
public:int search(vector<int>& nums, int target) {int n = nums.size();if (!n)return -1;if (n == 1)return nums[0] == target ? 0 : -1;int left = 0, right = n - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target)return mid;// 代表 [0,mid) 是有序的if (nums[0] <= nums[mid]) {if (nums[0] <= target && target < nums[mid]) {right = mid - 1;} else {left = mid + 1;}} else { // 表示 [mid,nums.size()) 是有序的if (nums[mid] < target && target <= nums[n - 1]) {left = mid + 1;} else {right = mid - 1;}}}return -1;}
};

5、寻找旋转排序数组中的最小值

题目链接：寻找旋转排序数组中的最小值
题目描述：
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

解答

我写的

根据对这道题目的理解，我写的代码如下：
借鉴的是上一题（搜索旋转排序数组）这道题目的解题思想，

• 如果 nums[left] <= nums[mid] ，说明在这个 [left,mid] 区间是有序的，且最小的值就是 nums[left]，这样将 left 指针移动到 mid+1 位置即可,然后再找剩下区间中的最小值。
• 如果不满足上述条件，则 [mid, nums.size()-1] 这个区间是有序的，且最小值为 nums[mid]，这样将 right 指针移动到 mid-1 位置即可，然后再找剩下区间中的最小值。

class Solution {
public:int findMin(vector<int>& nums) {int target = nums[0];int len = nums.size();int left = 0;int right = len - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[left] <= nums[mid]) {target = min(target, nums[left]);left = mid + 1;} else {target = min(target, nums[mid]);right = mid - 1;}}return target;}
};

官方写的

数组中元素的一般分布如下：

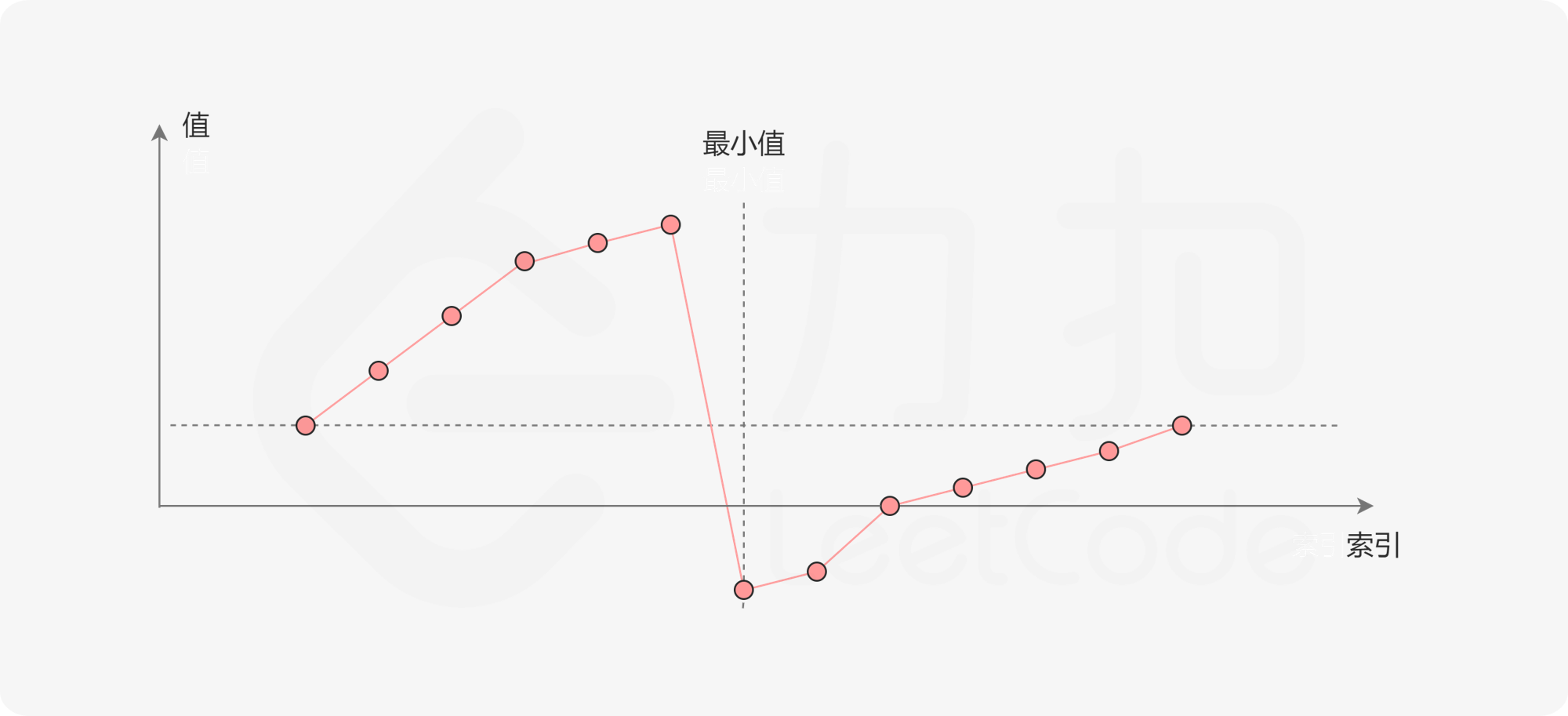
只有下面的两种情况：

情况一：nums[mid] < nums[right]

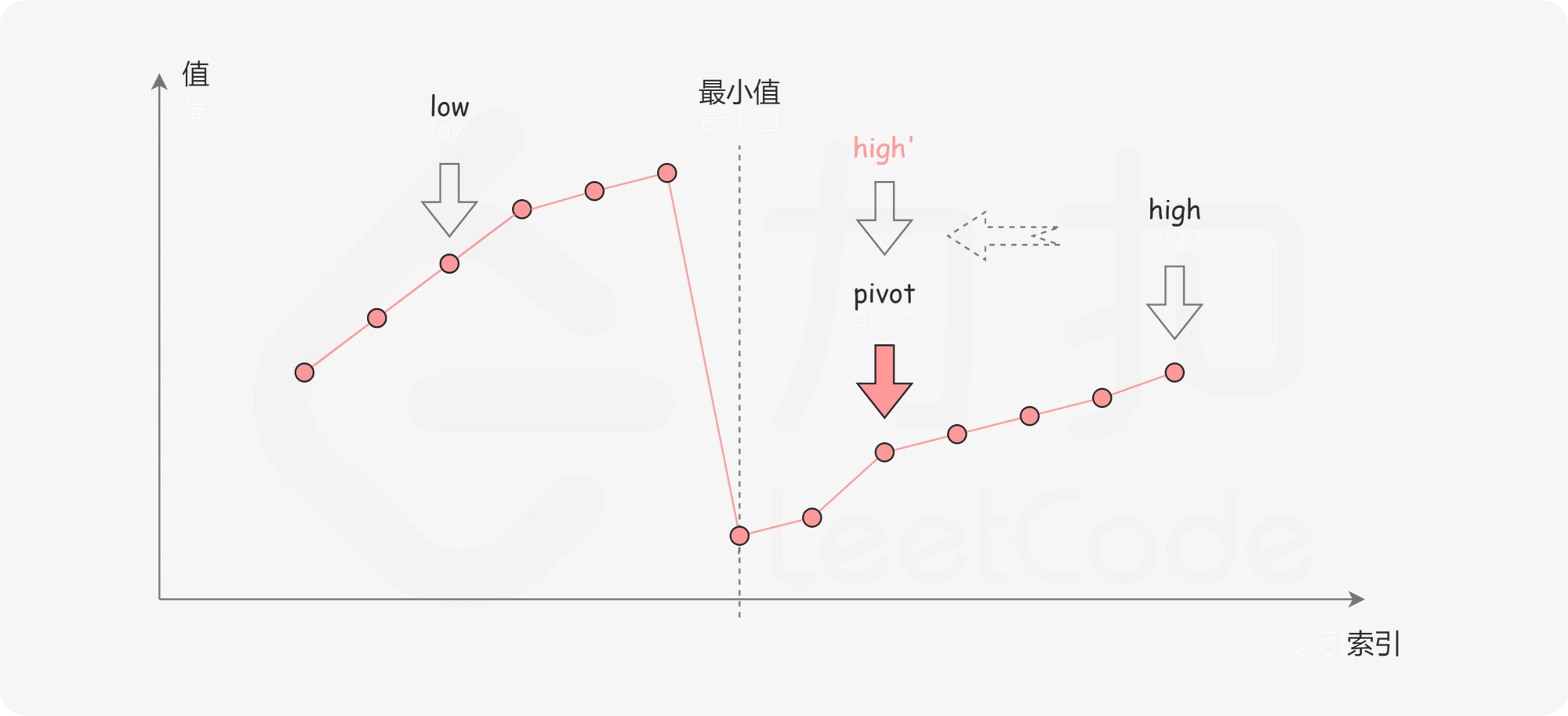
情况二：除开情况一的其他情况

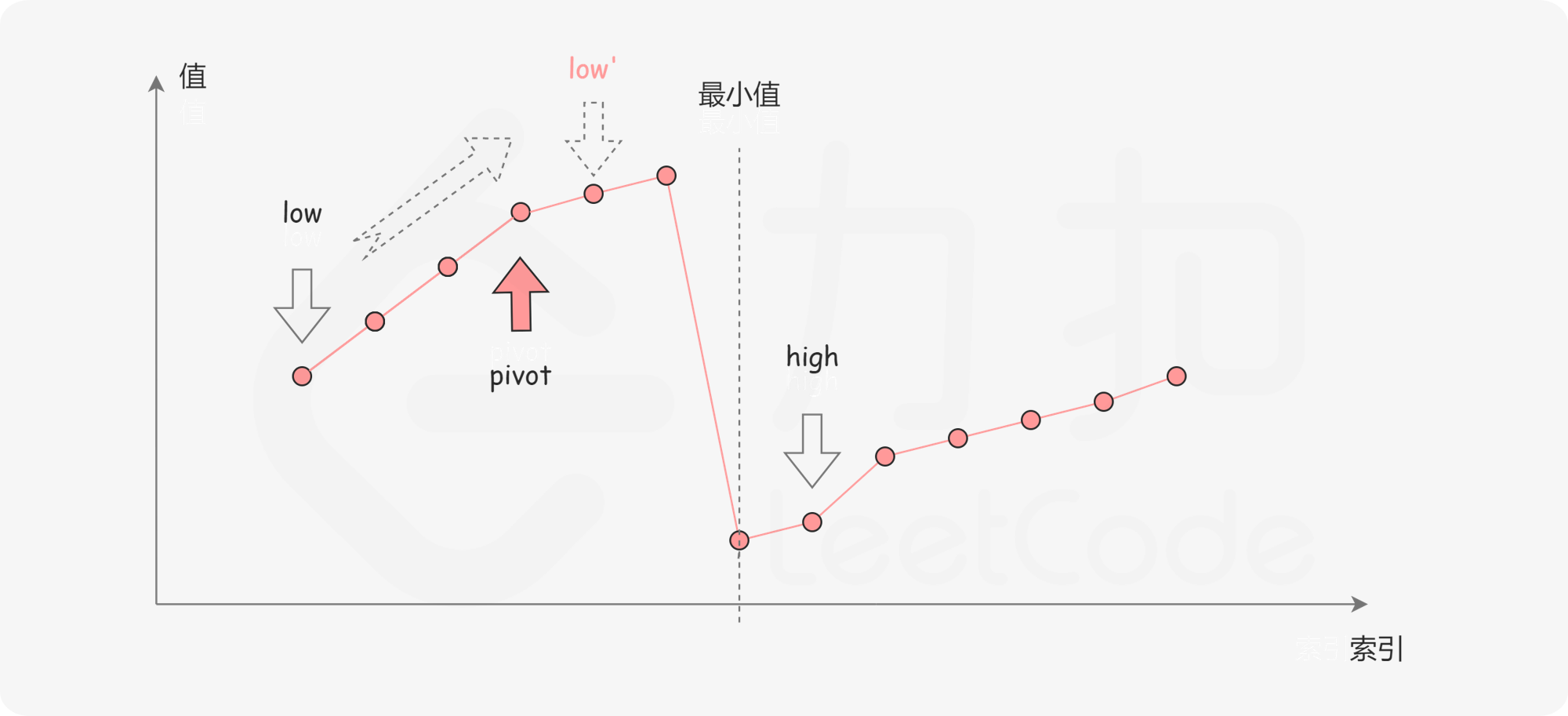
class Solution {
public:int findMin(vector<int>& nums) {int left = 0;int right = nums.size() - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < nums[right])right = mid;elseleft = mid + 1;}return nums[left];}
};

6、寻找两个正序数组的中位数

题目链接：寻找两个正序数组的中位数
题目描述：
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

解答

方法一：二分查找

这题我第一次做，没有啥思路，还是直接看的官方解答：

/* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较* 这里的 "/" 表示整除* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个* 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个* 这样 pivot 本身最大也只能是第 k-1 小的元素* 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组* 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组* 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数*/作者：力扣官方题解
链接：https://leetcode.cn/problems/median-of-two-sorted-arrays/solutions/258842/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution {
public:int getKthElement(const vector<int>& nums1, const vector<int>& nums2,int k) {int m = nums1.size();int n = nums2.size();int index1 = 0;int index2 = 0;while (true) {// 边界情况if (index1 == m)return nums2[index2 + k - 1];if (index2 == n)return nums1[index1 + k - 1];if (k == 1)return min(nums1[index1], nums2[index2]);// 一般情况int new_index1 = min(index1 + k / 2 - 1, m - 1);int new_index2 = min(index2 + k / 2 - 1, n - 1);int pivot1 = nums1[new_index1];int pivot2 = nums2[new_index2];if (pivot1 <= pivot2) {k -= new_index1 - index1 + 1;index1 = new_index1 + 1;} else {k -= new_index2 - index2 + 1;index2 = new_index2 + 1;}}}double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int nums1_len = nums1.size();int nums2_len = nums2.size();int total_length = nums1_len + nums2_len;if (total_length % 2 == 1)return getKthElement(nums1, nums2, (total_length + 1) / 2);elsereturn (getKthElement(nums1, nums2, total_length / 2) +getKthElement(nums1, nums2, total_length / 2 + 1)) /2.0;}
};

方法二：划分数组

对于 nums1 使用一个分割点 i ，对于 nums2 使用一个分割点 j ,使得如下图，蓝色部分划分为一个区域（元素个数记为 nums1_i），剩下的部分划分为一个区域（其中的元素个数记为 nums2_j）。满足要是两数组的元素个数和为偶数，则两区域元素个数相等；要是两数组的元素个数和为奇数，则 nums1_i = nums2_j + 1 。

且还需要满足以下四个条件：
$$\begin{array}{rl}& \text{num1}[i-1]<\text{num1}[i]（已经满足）\\ & \text{num1}[i-1]<\text{num2}[j]\\ & \text{num2}[j-1]<\text{num2}[j]（已经满足）\\ & \text{num2}[j-1]<\text{num1}[i]\end{array}$$

可以看成一根绳子（图中蓝色线），这根绳子的长度是固定的，保证有（$2\ast (i+j)=nums1.size()+nums2.size()+1$）,这样对数组 nums1 数组进行二分即可。保证第一个的数组长度小于第二个数组长度，不满足就交换一下数组即可，这个好处理。

如果：

• $nums1[i-1]>nums2[j]$ ， 说明绳子在第一个数组上面取值偏右了，需要左移一个单位。
• $nums2[j-1]>nums1[i]$ ， 说明绳子在第一个数组上面取值偏左了，需要右移一个单位。

还有一些边界条件需要处理：

• 要是绳子的一头到了 nums1 的第一个位置，这样的话，其左侧是没有元素了的，给其赋值 INT_MIN 即可。
• 要是绳子的一头到了 nums1 的最后一个位置了，这样的话，其右侧是没有元素了的，给其赋值 INT_MAX 即可。
• 对于数组 nums2 的边界处理方法与上面一样。
  
  
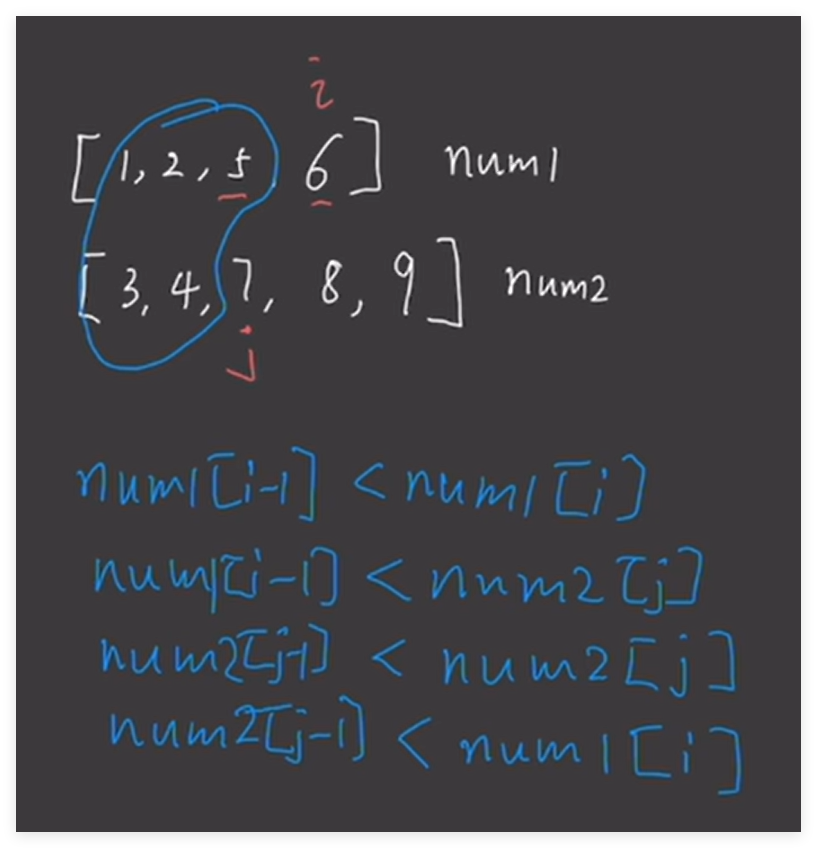
  于是根据上面的思路，可以编写代码如下：

class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {if (nums1.size() >nums2.size()) // 保证第一个数组的长度小于第二个数组的长度swap(nums1, nums2);int m = nums1.size();int n = nums2.size();int left = 0, right = m;while (left <= right) {int i = (left + right) / 2;  // 对第一个数组进行二分int j = (m + n + 1) / 2 - i; // 绳子的另一端(绳子长度是固定的)// 注意：i or j 左侧在绳子上，i or j 以及其右侧不在绳子上// 绳子的一侧在第一个数组上边界情况的处理int left1 = (i == 0) ? INT_MIN : nums1[i - 1];int right1 = (i == m) ? INT_MAX : nums1[i];// 绳子的另一侧在第二个数组上边界情况的处理int left2 = (j == 0) ? INT_MIN : nums2[j - 1];int right2 = (j == n) ? INT_MAX : nums2[j];// 满足那四个条件，这样再判断奇偶，返回结果即可if (left1 <= right2 && left2 <= right1) {if ((m + n) % 2 == 1) {return max(left1, left2);}return ((max(left1, left2) + min(right1, right2)) / 2.0);} else if (left1 > right2) { // 说明 i 的取值偏右了，左移一个单位right = i - 1;} else { // 说明 i 的取值偏左了，右移一个单位left = i + 1;}}return 0;}
};