当前位置： 首页 > news >正文

DAY14-新世纪DL（DeepLearning/深度学习）战士：破（优化算法）2

news 2025/8/23 21:13:59

本文参考文章0.0 目录-深度学习第一课《神经网络与深度学习》-Stanford吴恩达教授-CSDN博客

1.mini-batch梯度下降

优化算法是使你的神经网络运行更快，快速训练模型

向量化能让你快速处理m个样本，所以要把训练样本放入向量中X=\begin{bmatrix} x^{(1)}x^{(2)}x^{(3)}..x^{(m)} \end{bmatrix}，同理对于Y，

在对整个训练集执行梯度下降法时，你要做的是，你必须处理整个训练集，然后才能进行一步梯度下降法，你可以把训练集分割为小一点的子集训练，这些子集被取名为mini-batch，比如说将x^{(1)}到x^{(1000)}称为X^{(1)}，同理类推，对Y也是同样处理

而miin-batch梯度下降步骤和普通的梯度下降一致，不过对象由X,Y变为X^{​{t}},Y^{​{t}},使用batch梯度下降法，一次遍历训练集只能让你做一个梯度下降，使用mini-batch梯度下降法，一次遍历训练集，能让你做多个梯度下降。当然正常来说你想要多次遍历训练集，还需要为另一个while循环设置另一个for循环。所以你可以一直处理遍历训练集，直到最后你能收敛到一个合适的精度。

如果你有一个丢失的训练集，mini-batch梯度下降法比batch梯度下降法运行地更快，所以几乎每个研习深度学习的人在训练巨大的数据集时都会用到

代码：

import numpy as npdef mini_batch_gradient_descent(X, y, learning_rate=0.01, epochs=100, batch_size=32):n_samples, n_features = X.shapetheta = np.zeros(n_features)for _ in range(epochs):indices = np.random.permutation(n_samples)X_shuffled = X[indices]y_shuffled = y[indices]for i in range(0, n_samples, batch_size):X_batch = X_shuffled[i:i+batch_size]y_batch = y_shuffled[i:i+batch_size]gradient = 2/batch_size * X_batch.T.dot(X_batch.dot(theta) - y_batch)theta -= learning_rate * gradientreturn theta

2.理解mini-batch梯度下降

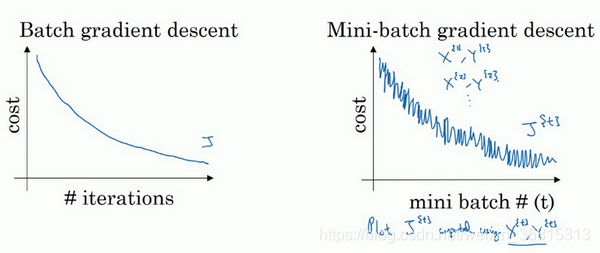
你需要决定的变量之一是mini-batch的大小，m 就是训练集的大小，极端情况下，如果mini-batch的大小等于m ，其实就是batch梯度下降法，每个迭代需要处理大量训练样本，该算法的主要弊端在于特别是在训练样本数量巨大的时候，单次迭代耗时太长。另一个极端情况，假设mini-batch大小为1，就有了新的算法，叫做随机梯度下降法，每个样本都是独立的mini-batch，但是你会失去所有向量化带给你的加速，因为一次性只处理了一个训练样本，这样效率过于低下

用mini-batch梯度下降法，我们从这里开始，一次迭代这样做，两次，三次，四次，它不会总朝向最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向，它也不一定在很小的范围内收敛或者波动。如果mini-batch大小既不是1也不是m ，应该取中间值，那应该怎么选择呢？其实是有指导原则的。

首先，如果训练集较小，直接使用batch梯度下降法，样本集较小就没必要使用mini-batch梯度下降法，你可以快速处理整个训练集，所以使用batch梯度下降法也很好，这里的少是说小于2000个样本，这样比较适合使用batch梯度下降法。不然，样本数目较大的话，一般的b大小为64到512，考虑到电脑内存设置和使用的方式，如果mini-batch大小是2的n 次方，代码会运行地快一些

最后需要注意的是在你的mini-batch中，要确保X^{t},Y^{t}要符合CPU/GPU内存，取决于你的应用方向以及训练集的大小。如果你处理的mini-batch和CPU/GPU内存不相符，不管你用什么方法处理数据，你会注意到算法的表现急转直下变得惨不忍睹

3.指数加权平均

接下来的几个优化算法，比梯度下降快，要理解这些算法，需要用到指数加权平均

给定序列数据$x_t$和衰减因子$\beta$（通常$\beta \in [0,1)$），指数加权平均值$v_t$的计算公式为v_t = \beta v_{t-1} + (1 - \beta) x_t，

其中：v_t是当前时刻的加权平均值。v_{t-1}是上一时刻的加权平均值。\beta控制权重衰减速度（越大，历史数据影响越持久）

4.偏差修正

偏差修正，可以让平均数运算更加准确

当初始阶段（t 较小时），根据指数加权平均v_t = \beta v_{t-1} + (1 - \beta) x_t，v_t可能因初始值（如 v_0=0）而低估真实均值。

此时需要偏差修正：v_t^{\text{corrected}} = \frac{v_t}{1 - \beta^t}，当t增大时，\beta^t \to 0，修正效果逐渐消失

$\beta$较小（如0.1）：对近期变化敏感，适合快速适应新趋势。

$\beta$较大（如0.9）：结果更平滑，但可能滞后于真实变化。

在机器学习中，在计算指数加权平均数的大部分时候，大家不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果你关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能帮助你在早期获取更好的估测。

5.动量梯度下降法

动量梯度下降法的运行速度几乎总是快于标准的梯度下降法，简而言之，基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新你的权重。

动量梯度下降法是梯度下降算法的一种改进版本，通过引入动量项加速收敛并减少震荡。其核心思想是模拟物理中的动量概念，即当前更新方向不仅依赖当前梯度，还受历史梯度方向的影响。

更新公式：v_t = \beta v_{t-1} + (1 - \beta) \nabla_\theta J(\theta)，\theta = \theta - \alpha v_t

其中：

v_t是当前动量项，$v_{t-1}$是上一时刻的动量。

\beta是动量系数（常用值为 0.9，可根据任务调整（如 0.8-0.99）），控制历史梯度对当前方向的影响。

\alpha是学习率（通常需比普通梯度下降更小，因动量会放大更新幅度）。

\nabla_\theta J(\theta)是损失函数关于参数\beta的梯度。

初始化参数：设置初始参数 $\theta$、学习率 $\alpha$、动量系数 $\beta$（如 0.9），初始化动量项 $v=0$。

迭代更新：每次迭代计算当前梯度 \nabla_\theta J(\theta)，并更新动量项v和$\theta$

v = \beta v + (1 - \beta) \nabla_\theta J(\theta)，\theta = \theta - \alpha v

def momentum_gradient_descent(theta, alpha, beta, num_iterations, gradient_function):v = 0for _ in range(num_iterations):grad = gradient_function(theta)v = beta * v + (1 - beta) * gradtheta = theta - alpha * vreturn theta

6.RMSprop

RMSprop算法，全称是root mean square prop算法，它也可以加速梯度下降

RMSprop是一种自适应学习率优化算法。它通过调整每个参数的学习率来加速梯度下降的收敛，特别适合处理非平稳目标函数或稀疏梯度问题。RMSprop 是 AdaGrad 的改进版本，解决了 AdaGrad 学习率单调下降的问题。

核心思想：RMSprop 通过计算梯度平方的指数移动平均来调整学习率。对于频繁更新的参数，其梯度平方的累积值较大，从而降低学习率；对于稀疏更新的参数，累积值较小，学习率相对较高。

初始化参数：

全局学习率 $\eta$

初始参数\theta _0

衰减率\rho（通常设为 0.9）（控制历史信息的权重，值越大对过去梯度依赖越强。）

小常数\varepsilon（通常为 $10^{-8}$，防止除以零）

初始累积变量 $E[g^2]_0 = 0$。

计算梯度
在第t次迭代中，计算当前参数 $\theta_t$的梯度$g_t$：g_t = \nabla_\theta J(\theta_t)

初始化梯度平方的指数移动平均E[g^2]t = \rho \cdot E[g^2]{t-1} + (1 - \rho) \cdot g_t^2

迭代更新：

调整学习率并更新参数\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \cdot g_t

import numpy as npdef rmsprop(params, grads, lr=0.01, rho=0.9, epsilon=1e-8):cache = np.zeros_like(params)  # 初始化累积变量cache = rho * cache + (1 - rho) * grads**2updated_params = params - lr * grads / (np.sqrt(cache) + epsilon)return updated_params

7.Adam优化算法

Adam（Adaptive Moment Estimation）是一种结合了动量（Momentum）和RMSProp思想的梯度下降优化算法，适用于大规模数据或参数的场景。它通过计算梯度的一阶矩（均值）和二阶矩（未中心化的方差）的自适应估计，实现对学习率的动态调整。

每个参数有独立的学习率，适合处理稀疏数据。

初期迭代时，$m_t$和$v_t$偏向零，修正后加速初期收敛。

常用于深度学习中的卷积网络、循环网络等。

核心思想：

动量机制：记录梯度的指数加权移动平均值（一阶矩），保留历史梯度方向信息，加速收敛。

自适应学习率：通过梯度的平方的指数加权移动平均（二阶矩）调整参数的学习率，解决稀疏梯度问题。

初始化参数：

初始参数 $\theta_0$

一阶矩变量 $m_0 = 0$，二阶矩变量$v_0 = 0$

衰减率 $\beta_1$（通常为0.9），$\beta_2$（通常为0.999）

学习率 $\alpha$（默认0.001，可尝试$[0.001, 0.0001]$。）

小常数 $\epsilon$（默认保持$10^{-8}$，防止除以零）

迭代跟新（对于第t步）：

计算当前梯度：$g_t = \nabla_\theta J(\theta_{t-1})$

更新一阶矩：$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

更新二阶矩：$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

修正一阶矩偏差：$\hat{m}_t = m_t / (1 - \beta_1^t)$

修正二阶矩偏差：$\hat{v}_t = v_t / (1 - \beta_2^t)$

更新参数：$\theta_t = \theta_{t-1} - \alpha \cdot \hat{m}_t / (\sqrt{\hat{v}_t} + \epsilon)$

import torch
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999))

8.学习率衰减

学习率衰减（Learning Rate Decay）是优化神经网络训练过程的常用技术，通过逐步降低学习率，帮助模型在训练初期快速收敛，后期稳定精细调整。合理的学习率衰减策略能避免振荡、提升泛化能力。

这里举例指数衰减（其他的衰减可以找其他文章详细学习，本文仅提一嘴）

学习率按指数函数连续衰减，适用于需要平滑调整的场景。

公式：\alpha_t = \alpha_0 \times \gamma^{t}（γ 为衰减率（通常接近 1，如 0.95））

9.局部最优问题

局部最优问题指在优化过程中，算法收敛到一个局部最优解而非全局最优解。该解在邻近区域内是最优的，但在整个解空间中可能存在更优的解。这种现象常见于非凸优化、梯度下降算法或启发式搜索中。

我们从深度学习历史中学到的一课就是，我们对低维度空间的大部分直觉，比如你可以画出上面的图，并不能应用到高维度空间中。适用于其它算法，因为如果你有2万个参数，那么 J 函数有2万个维度向量，你更可能遇到鞍点，而不是局部最优点。

如果局部最优不是问题，那么问题是什么？结果是平稳段会减缓学习，平稳段是一块区域，其中导数长时间接近于0，如果你在此处，梯度会从曲面从从上向下下降，因为梯度等于或接近0，曲面很平坦，你得花上很长时间慢慢抵达平稳段的这个点，因为左边或右边的随机扰动

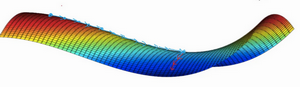
我们可以沿着这段长坡走，直到这里，然后走出平稳段。

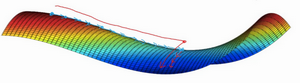
首先，你不太可能困在极差的局部最优中，条件是你在训练较大的神经网络，存在大量参数，并且成本函数 J 被定义在较高的维度空间。

第二点，平稳段是一个问题，这样使得学习十分缓慢，这也是像Momentum或是RMSprop，Adam这样的算法，能够加速学习算法的地方。在这些情况下，更成熟的优化算法，如Adam算法，能够加快速度，让你尽早往下走出平稳段。

10.习题参考

2.11 总结-深度学习第二课《改善深层神经网络》-Stanford吴恩达教授_batch的大小通常不是1也不是m,而是介于两者之间?-CSDN博客

http://www.xdnf.cn/news/1349065.html

相关文章：

  • 多线程下为什么用ConcurrentHashMap而不是HashMap
  • 【Android】 连接wifi时，强制应用使用流量
  • 【从零开始java学习|第九篇】方法的相关知识与练习
  • 【微服务的数据一致性分发问题】究极解决方案
  • 日志的配置
  • 一键部署openGauss6.0.2轻量版单节点
  • Spring原理
  • 最近 | 黄淮教务 | 小工具合集
  • 世界模型一种能够对现实世界环境进行仿真，并基于文本、图像、视频和运动等输入数据来生成视频、预测未来状态的生成式 AI 模型
  • Maxscript如何清理3dMax场景？
  • 打工人日报20250822
  • More Effective C++ 条款01：仔细区别 pointers 和 references
  • Java设计模式-外观模式
  • 滑动窗口+子串+普通数组算法
  • Elasticsearch搜索原理
  • HEVC（H.265）与HVC1的关系及区别
  • Unreal Engine UProjectileMovementComponent
  • 异步开发的三种实现方式
  • Unreal Engine USceneComponent
  • Unreal Engine Simulate Physics
  • 线段树01
  • 20250822 组题总结
  • 如何解决pip安装报错ModuleNotFoundError: No module named ‘uvicorn’问题
  • 北京-测试-入职甲方金融-上班第三天
  • 嵌入式第三十五天(网络编程(UDP))
  • GPS欺骗式干扰的产生
  • DSPy框架：从提示工程到声明式编程的革命性转变
  • 声网SDK更新，多场景抗弱网稳定性大幅增强
  • GaussDB GaussDB 数据库架构师修炼(十八)SQL引擎(1)-SQL执行流程
  • week3-[二维数组]小方块