当前位置：首页 > news >正文

线段树01

news 2025/8/23 20:26:47

线段树的 5 个基本操作：

（1）push_up(u)：传入一个节点编号，更新节点信息

（2）build()：将一段区间初始化为线段树

（3）modify(): 修改操作，分两种，一种是修改单点信息，一种是修改区间（需要用到push_down和 lazy_tag）

（4）query()：查询操作

（5）push_down()：区间修改需要用到的操作

概念引入

概括地说，线段树是一种基于 分治思想 的 二叉树 结构，用于在区间上进行信息统计。与按照二进制位（2 的次幂）进行区间划分的树状数组相比，线段树是一种更加通用的数据结构，功能比树状数组更强大：

线段树的每个节点都代表一个 区间/线段 （每个节点都维护对应子树的一些信息）。
线段树具有唯一的根节点，代表的区间是整个统计范围，如 [1,N][1,N] 。
线段树的叶节点都代表一个长度为 11 的元区间 [x,x][x,x] 。
对于 每个内部节点 [l,r][l,r] ，它的左子节点是 [l,mid][l,mid] ，右子节点是 [mid+1,r][mid+1,r] ，其中 mid=(l+r)>>1mid=(l+r)>>1
线段树是一棵二叉树，一个区间每次折一半往下分，包含 nn 个元素的线段树，最多分 log⁡nlogn 次就到达最低层。需要查找一个点或者区间的时候，顺着结点往下找， 最多 log⁡nlogn 次就能找到 。
结点所表示的“线段”的值，可以是区间和、最值或者其他根据题目灵活定义的值。

比如说一个长度为 1010 的线段，我们可以表示成这样：

上面例子中，对应的线段树结构如下图所示：

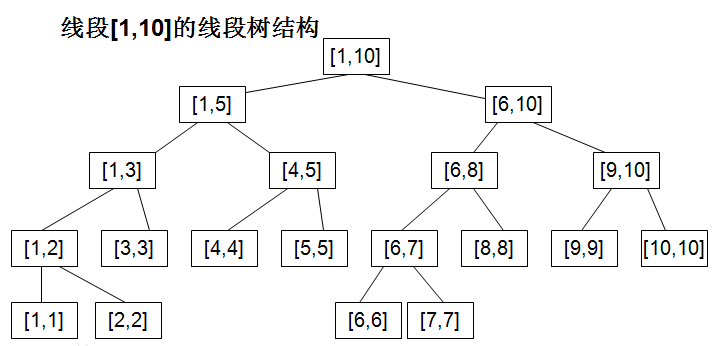
o_segment_tree

上图展示了一棵线段树。可以发现，除去树的最后一层，整棵线段树一定是一棵 完全二叉树 ，树的深度为 O(log⁡N)O(logN) 。因此，我们可以按照完全二叉树的存储方法来保存节点间的关系:

根节点编号为 11 。
编号为 xx 的节点的左子节点编号为 2x2x ，右子节点编号为 2x+12x+1 。

这样一来，我们就能简单地使用一个结构体数组来保存线段树。当然，树的最后一层节点在数组中保存的位置不是连续的，直接空出数组中多余的位置即可。

在理想情况下， NN 个叶节点的满二叉树有 N＋N/2+N/4+⋯+2+1=2N−1N＋N/2+N/4+⋯+2+1=2N−1 个节点。因为在上述存储方式下，最后还有一层可能产生了空余，所以保存线段树的数组长度要 不小于 4N4N 才能保证不会越界。

考查每个线段 [L,R][L,R] ， LL 是左端， RR 是右端：

L=RL=R ，说明这个结点只有一个元素，它是一个叶子结点。
L<RL<R ，说明这个结点代表的不只一个点，那么它有两个儿子，左儿子区间是 [L,Mid][L,Mid] ，右儿子区间是 [Mid+1,R][Mid+1,R] ，其中 Mid=(L+R)/2Mid=(L+R)/2 。例如： L=1,R=5,Mid=3L=1,R=5,Mid=3 ，左儿子是 [1,3][1,3] ，右儿子是 [4,5][4,5] 。

线段树的构建

线段树是除了最后一层之外，其他层都是满的一种树，这点和堆（完全二叉树）是一样的，因此可以使用(静态)一维数组来保存整棵树。

对于编号是 xx 的节点，和其相关的节点关系如下：

编号是x{父亲节点：⌊x2⌋,或写为x>>1左儿子：2x,或写为x<<1右儿子：2x+1,或写为x<<1∣1编号是x⎩⎪⎪⎨⎪⎪⎧父亲节点：⌊2x⌋,或写为x>>1左儿子：2x,或写为x<<1右儿子：2x+1,或写为x<<1∣1

PS:上述两种写法都一样，表面上第二种速度最快，但现代编译器会将除二和加一操作优化为右式，所以编译后速度一样。（不过第二种看着更高级）

编码时，可以定义标准的二叉树数据结构；在竞赛中一般用静态数组实现的满二叉树，虽然比较浪费空间，但是编码稍微简单一点。

下面给的代码，都用静态分配的 tree[]tree[] 。父结点和子结点之间的访问非常简单，缺点是最后一行有大量结点被浪费。

// 定义根结点是tree[1]，即编号为1的结点是根
// 第一种方法：定义二叉树数据结构
struct{int l, r, data;          // 用tree[i].data记录线段i的最值或区间和
} tree[N*4];                 // 分配静态数组，开4倍大// 第二种方法：直接用数组表示二叉树，更节省空间，在竞赛中一般用此方法
int tree[N*4];	             // 用tree[i]记录线段i的最值或区间和
// 结点p是父结点, ls(p)是左儿子，rs(p)是右儿子
inline int ls(int x){ return x<<1;  }     // 左儿子 l，编号是 p*2
inline int rs(int x){ return x<<1|1;}     // 右儿子 r，编号是 p*2+1

线段树的基本用途是对序列进行维护，支持查询与修改指令。给定一个长度为 NN 的序列 AA ，我们可以在区间 [1,N][1,N] 上建立一棵线段树，每个叶节点 [i,i][i,i] 保存 A[i]A[i] 的值。线段树的二叉树结构可以很方便地 从下往上 传递信息。以区间最大值问题为例，记 dat(l,r)dat(l,r) 等于 max⁡l≤i≤r{A[i]}maxl≤i≤r{A[i]} ，显然 dat(l,r)=max(dat(l,mid),dat(mid+1,r))dat(l,r)=max(dat(l,mid),dat(mid+1,r)) 。

下面这段代码建立了一棵线段树并在每个节点上保存了对应区间的最大值。

inline void push_up(int p){                     // 从下往上传递区间值// tree[p] = tree[p<<1] + tree[p<<1|1];     // 求区间和tree[p] = max(tree[p<<1], tree[p<<1|1]);    // 求区间最大值
}
void build(int p,int l,int r){             // 结点编号 p 指向区间[l, r]if(l==r) {                             // 最底层的叶子，存叶子的值tree[p]=a[l];return;}   int mid = (l + r) >> 1;                // 分治：折半build(p<<1, l, mid);                   // 递归左儿子build(p<<1|1, mid+1, r);               // 递归右儿子push_up(p);                            // 从下往上传递区间值
}
// 建树的入口
build(1, 1, n);

在线段树中，根节点是执行各种操作的入口。

线段树的单点修改

操作：形如 C x k，把区间的第 xx 位加上 kk

这个代码比较好写， 从根节点开始 ，看这个 xx 是在左子树还是在右子树，递归查找，直到找到该叶子节点。需要注意的是在返回的时候， 最后不能漏掉 push_up 操作，来更新所有受到该叶子节点影响的父节点 。

代码如下：

// 单点修改, x 位增加 k
void modify(int x, int k, int p, int l, int r)  // l: p 对应区间的左端点， r: p 对应区间的右端点
{if(l == r) {   // 叶子节点tree[p] += k;return;}int mid = (l + r) >> 1;if(x <= mid)  modify(x, k, p*2, l, mid);   // 在左子树else  modify(x, k, p*2+1, mid+1, r);		 // 在右子树push_up(p);    // 从下往上传递区间值
}// 调用入口
modify(x, k, 1, 1, n);

线段树的区间查询

操作：形如 Q l r，查询区间 [l,r][l,r] 上的信息（区间和、最大值、最小值等）。

根据分治的思想，某一个区间上的和目标区间的交集和的计算方式为：

交集和=左区间上的交集部分和+右区间上的交集部分和交集和=左区间上的交集部分和+右区间上的交集部分和

具体实现起来，总体思路为：

如果这个区间被完全包括在目标区间里面，直接返回这个区间的值
如果这个区间的左儿子和目标区间有交集，那么搜索左儿子
如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

示例代码

以求解区间和为例，实现的示例代码如下：

// 区间查询（区间和）
int query(int ql, int qr, int p, int l, int r)
{if(ql <= l && r <= qr)   return tree[p];   // 当前区间完全包含于查询的区间，直接返回该区间值int ans = 0;int mid = (l + r) >> 1;if(ql <= mid)								// 如果这个区间的左儿子和目标区间又交集，那么搜索左儿子ans += query(ql, qr, p<<1, l, mid);if(mid < qr)                                // 如果这个区间的右儿子和目标区间又交集，那么搜索右儿子ans += query(ql, qr, p<<1|1, mid+1, r);return ans;
}
// 求区间 [L,R] 的和的调用方式：query(L, R, 1, 1, n)// 求区间和 —— 结构体示例写法
int query(int i,int l,int r){int s = 0;if(tree[i].l>=l && tree[i].r<=r)             // 如果这个区间被完全包括在目标区间里面，直接返回这个区间的值return tree[i].sum;int s=0;if(tree[i*2].r>=l)  s+=query(i*2,l,r);       // 如果这个区间的左儿子和目标区间又交集，那么搜索左儿子if(tree[i*2+1].l<=r)  s+=query(i*2+1,l,r);   // 如果这个区间的右儿子和目标区间又交集，那么搜索右儿子return s;
}

以查询区间 [l,r][l,r] 的和为例，给出代码。查询递归到某个结点 pp （ pp 表示的区间是 [pl,pr][pl,pr] ）时，有 33 种情况：

[l,r][l,r] 完全覆盖了 [pl,pr][pl,pr] ，即 l≤pl≤pr≤rl≤pl≤pr≤r ，直接返回节点 pp 存储的值即可。
[l,r][l,r] 与 [pl,pr][pl,pr] 不相交，即 l>prl>pr 或者 r<plr<pl ，退出（ 这种情况在代码里不存在，因为初始区间 [1,n] 肯定包含目标区间 ）。
[l,r][l,r] 与 [pl,pr][pl,pr] 部分重叠，分别搜左右子结点。 l<prl<pr ，继续递归左子结点，例如查询区间[4, 9]，与第2个结点[1, 5]有重叠，因为4 < 5。R > pl，继续递归右子结点，例如[4, 9]与第3个结点[6, 10]有重叠，因为9 > 6。

这种查询过程会把询问的区间 [l,r][l,r] 在线段树上划分成 O(log⁡N)O(logN) 个节点，然后再求解区间信息。

至此，线段树已经能够像 ST 算法一样，处理区间最值，也能像树状数组一样，处理区间上的单点修改和区间查询问题。下面做一些练习题巩固一下。

练习题

P2324 树状数组 1 ：单点修改，区间查询 - TopsCoding
P4672 你能回答这些问题吗 - TopsCoding —— 线段树 + 子段和
P4691 敌兵布阵 - TopsCoding

区间修改，单点查询

区间修改和单点查询，我们的思路就变为：如果把这个区间加上 kk ，相当于把这个区间涂上一个 kk 的标记，然后单点查询的时候，就从上跑到下，把沿路的标记加起来就好。因此， 这类操作里，不需要 push_up 操作！建树时也是如此！

这里面给区间贴标记的方式与上面的区间查找类似，原则还是那三条，只不过第一条： 如果这个区间被完全包括在目标区间里面，直接返回这个区间的值 变为了 如果这个区间被完全包括在目标区间里面，将这个区间增加 k 。

区间修改代码：

// 区间修改：[ql, qr] 增加 k
void modify(int ql, int qr, int p,int l,int r, int k){if(ql <= l && r <= qr)   // 如果这个区间被完全包括在目标区间里面，将这个区间标记k{tr[p] += k;return ;}int mid = (l + r) >> 1;if(ql <= mid)    // 包含部分左区间modify(ql, qr, p*2, l, mid, k);if(qr > mid)     // 包含部分右区间modify(ql, qr, p*2+1, mid+1, r, k);// 注意，无 push_up 操作
}

单点查询，查找区间的第 xx 位。这个更好实现，就是 xx 哪往哪跑，把路径上所有的值加上就好了：

int query(int x, int p, int l, int r){int ans = 0;ans += tr[p];if(l == r)return ans;int mid = (l + r )>>1;if(x <= mid) ans += query(x, p << 1, l, mid);else ans += query(x, p<<1|1, mid+1, r);return ans;
}

这样的线段树，除了求和，还可以求区间最小最大值，还可以区间染色。

但是，这样的线段树展现不出来她的魅力。因为区间求和，树状数组比它少了一个很大的常数(树状数组常数是 11 ，线段树常数平均约为 44 )。而区间最值，ST 的那神乎其技的 O(n)O(n) 查询也能完爆它。

练习题

P4086 树状数组 2 ：区间修改，单点查询 - TopsCoding

线段树的区间修改 + 区间查询

本节介绍线段树的核心技术“ lazy-tag ”，并给出“区间修改+区间查询”问题的模板。

在树状数组这一节中，已经指出区间修改比单点修改复杂很多。最普通区间修改，例如对一个数列的 [l,r][l,r] 区间内每个元素统一加上 dd ，如果在线段树上，一个个地修改这些元素，那么 mm 次区间修改的复杂度是 O(mnlog⁡n)O(mnlogn) 的。

试想，如果我们在一次修改指令中发现节点 pp 代表的区间 [pl,pr][pl,pr] 被修改区间 [l,r][l,r] 完全覆盖，并且逐一更新了子树 pp 中的所有节点，但是在之后的查询指令中却根本没有用到 [l,r][l,r] 的子区间作为候选答案，那么更新 pp 的整棵子树就是徒劳的。

换言之，我们在执行修改指令时，同样可以在 l≤pl≤pr≤rl≤pl≤pr≤r 的情况下立即返回，只不过在回溯之前向节点 pp 增加一个标记，标识 “该节点曾经被修改，但其子节点尚未被更新”。

如果在后续的指令中，需要从节点 pp 向下递归，我们再检查 pp 是否具有标记。若有标记,就根据标记信息更新 pp 的两个子节点，同时为 pp 的两个子节点增加该标记，然后清除 pp 的标记（标记往下传）。这个标记，就被称为 lazy-tag。

lazy-tag

lazy-tag （又称懒惰标记，或者延迟标记）。当修改的是一个线段区间时，就只对这个线段区间进行整体上的修改，其内部每个元素的内容先不做修改， 只有当这个线段区间的一致性被破坏时 ，才把变化值传递给下一层的子区间。每次区间修改的复杂度是 O(log⁡n)O(logn) 的，一共 mm 次操作，总复杂度是 O(mlog⁡n)O(mlogn) 的。区间 ii 的 lazylazy 操作，用 tag[i]tag[i] 记录。

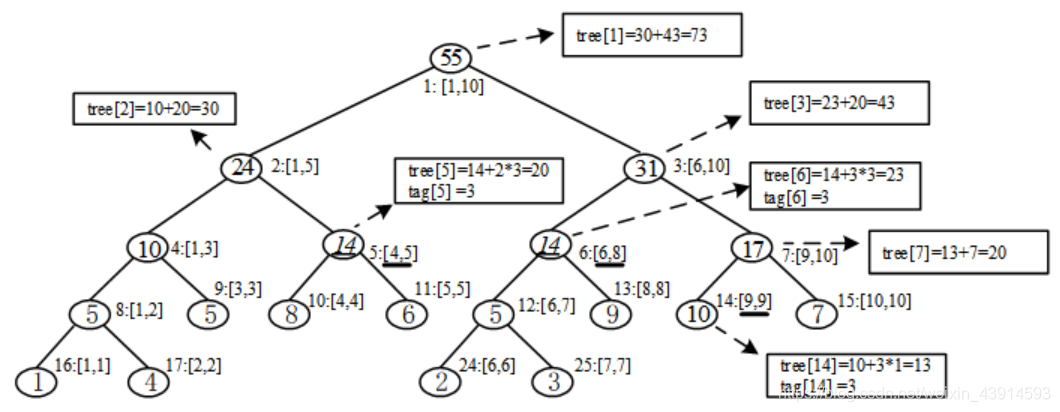
下面举例说明区间修改函数 update()update() 的具体步骤。例如把 [4,9][4,9] 区间内的每个元素加 33 ，执行步骤是：

（1）左子树递归到结点 55 ，即区间 [4,5][4,5] ，完全包含在 [4,9][4,9] 内，打标记 tag[5]=3tag[5]=3 ，更新 tree[5]tree[5] 为 2020 ，不再继续深入；

（2）左子树递归返回，更新 tree[2]tree[2] 为 3030 ；

（3）右子树递归到结点 66 ，即区间 [6,8][6,8] ，完全包含在 [4,9][4,9] 内，打标记 tag[6]=3tag[6]=3 ，更新 tree[6]tree[6] 为 2323 。

（4）右子树递归到结点 1414 ，即区间 [9,9][9,9] ，打标记 tag[14]=3tag[14]=3 ，更新 tree[14]=13tree[14]=13 ；

（5）右子树递归返回，更新 tree[7]=20tree[7]=20 ；继续返回，更新 tree[3]=43tree[3]=43 ；

（6）返回到根节点，更新 tree[1]=73tree[1]=73 。

详情见下图。

push down

push_down()函数 。在进行多次区间修改时，一个结点需要记录多个区间修改。而这些区间修改往往有冲突，例如做 22 次区间修改，一次是 [4,9][4,9] ，一次是 [5,8][5,8] ，它们都会影响 5:[4,5]5:[4,5] 这个结点。第一次修改 [4,9][4,9] 覆盖了结点 55 ，用 tag[5]tag[5] 做了记录；而第二次修改 [5,8][5,8] 不能覆盖结点 55 ，需要再向下搜到结点 11:[5,5]11:[5,5] ，从而破坏了 tag[5]tag[5] ，此时原 tag[5]tag[5] 记录的区间统一修改就不得不往它的子结点传递和执行了，传递后 tag[5]tag[5] 失去了意义，需要清空。所以 lazy−taglazy−tag 的主要操作是 解决多次区间修改 ，用 push_down() 函数完成。它首先检查结点 pp 的 tag[p]tag[p] ，如果有值，说明前面做区间修改时给 pp 打了 tagtag 标记，接下来就把 tag[p]tag[p] 传给左右子树，然后把 tag[p]tag[p] 清零。

push_down() 函数不仅在“区间修改”中用到，在“区间查询”中同样用到。

下面给出 P4087 的线段树代码，它是“区间修改+区间查询”的模板题。

模板题：P4087 树状数组 3 ：区间修改，区间查询 - TopsCoding

注意代码中对二叉树的操作，特别是反复用到的变量 plpl 和 prpr ，它们是结点 pp 所指向的原数列的区间位置 [pl,pr][pl,pr] 。 pp 是二叉树的某个结点，范围是 1≤p≤N∗41≤p≤N∗4 ；而 pl、prpl、pr 的范围是 1≤pl,pr≤n1≤pl,pr≤n ， nn 是数列元素的个数。用满二叉树实现线段树时，一个结点 pp 所指向的 [pl,pr][pl,pr] 是确定的，也就是说，给定 pp ，可以推算出它的 [pl,pr][pl,pr] 。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6 + 10;
ll a[N];      //记录数列的元素，从a[1]开始
ll tree[N << 2]; //tree[i]：第i个结点的值，表示一个线段区间的值，例如最值、区间和
ll tag[N << 2]; //tag[i]：第i个结点的lazy-tag，统一记录这个区间的修改void push_up(ll p) {             //从下往上传递区间值tree[p] = tree[p*2] + tree[p*2+1];// 本题是区间和。如果求最小值，改为：tree[p] = min(tree[ls(p)], tree[rs(p)]);
}
void build(ll p, ll l, ll r) {   // 建树。p是结点编号，它指向区间[pl, pr]tag[p] = 0;                  // lazy-tag标记if (l == r) {tree[p] = a[l];    // 最底层的叶子，赋值return;}ll mid = (l + r) >> 1;       // 分治：折半build(p*2, l, mid);          // 左儿子build(p*2+1, mid + 1, r);    // 右儿子push_up(p);                  // 从下往上传递区间值
}
inline void addtag(ll p, ll l, ll r, ll d) {  // 给结点p打tag标记，并更新treetag[p] += d;                   // 打上tag标记tree[p] += d * (r - l + 1);    // 计算新的tree
}
inline void push_down(ll p, ll l, ll r) {  //不能覆盖时，把tag传给子树if (tag[p]) {                     //有tag标记，这是以前做区间修改时留下的ll mid = (l + r) >> 1;addtag(p*2, l, mid, tag[p]); //把tag标记传给左子树addtag(p*2+1, mid + 1, r, tag[p]); //把tag标记传给右子树tag[p] = 0;                     //p自己的tag被传走了，归0}
}
void modify(ll ql, ll qr, ll p, ll l, ll r, ll d) { //区间修改：把[L, R]内每个元素加上dif (ql <= l && r <= qr) { // 完全覆盖，直接返回这个结点，它的子树不用再深入了addtag(p, l, r, d);   // 给结点p打tag标记，下一次区间修改到p这个结点时会用到return;}push_down(p, l, r);                     // 如果不能覆盖，把tag传给子树ll mid = (l + r) >> 1;if (ql <= mid) modify(ql, qr, p*2, l, mid, d); //递归左子树if (qr > mid)  modify(ql, qr, p*2+1, mid + 1, r, d); //递归右子树push_up(p);                               //更新
}
ll query(ll ql, ll qr, ll p, ll l, ll r) {//查询区间[L,R]；p是当前结点（线段）的编号，[pl,pr]是结点p表示的线段区间if (ql <= l && r <= qr) return tree[p];    // 完全覆盖，直接返回push_down(p, l, r);                      // 不能覆盖，把tag传给子树ll res = 0;ll mid = (l + r) >> 1;if (ql <= mid) res += query(ql, qr, p*2, l, mid);       // 左子节点有重叠if (qr > mid)  res += query(ql, qr, p*2+1, mid + 1, r); // 右子节点有重叠return res;
}
int main() {ios::sync_with_stdio(0);cin.tie(0);ll n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];build(1, 1, n);                 //建树while (m--) {ll op, l, r, x;cin >> op;if (op == 1) {                //区间修改：把[L,R]的每个元素加上xcin >> l >> r >> x;modify(l, r, 1, 1, n, x);} else {                      //区间询问：[L,R]的区间和cin >> l >> r;cout << query(l, r, 1, 1, n) << '\n';}}return 0;
}

具体的题目，可以根据情况选用树状数组和线段树。很多题目只能用线段树，如果两种都能用，建议先考虑用线段树。虽然线段树的代码长很多，但是更容易理解、编码更清晰。而且树状数组的局限性很大，即使能用，也常常需要经过较难的思维转换，区间修改就是一个例子（转差分数组）。