ICCV 2025 | Reverse Convolution and Its Applications to Image Restoration

• 标题：Reverse Convolution and Its Applications to Image Restoration
• 作者：Xuhong Huang, Shiqi Liu, Kai Zhang, Ying Tai, Jian Yang, Hui Zeng, Lei Zhang
• 单位：Nanjing University, The Hong Kong Polytechnic University, OPPO Research Institute
• 论文：https://arxiv.org/abs/2508.09824
• 代码：https://github.com/cszn/ConverseNet

convolution 和 transposed convolution 是神经网络中广泛使用的基础算子。然而，transposed convolution（又称 deconvolution）在数学形式上并非 convolution 的真正逆运算。迄今为止，尚未有 reverse convolution 算子被确立为神经架构的标准组件。
本文首次提出一种新颖的深度可分离 reverse convolution 算子，通过建立并求解正则化最小二乘优化问题，实现对 depthwise convolution 的有效反转。我们全面研究了其核初始化、padding 策略等关键实现细节。
基于此算子，我们进一步构建 reverse convolution block，将其与 layer normalization、1×1 convolution 和 GELU 激活结合，形成类 Transformer 结构。所提出的算子与 block 可直接替换现有架构中的常规 convolution 和 transposed convolution 层，从而构建 ConverseNet。
针对典型图像复原模型 DnCNN、SRResNet 和 USRNet，我们分别训练三种 ConverseNet 变体，用于高斯去噪、超分辨率和去模糊。
大量实验验证了所提 reverse convolution 算子作为基础构建模块的有效性。我们希望这项工作能够为深度模型设计中新算子的开发及其应用铺平道路。

研究背景

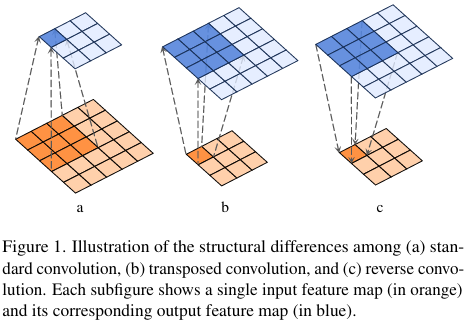
卷积和转置卷积（后面也称为反卷积 deconvolution）是深度神经网络中常用的基本操作。卷积用于特征提取并可以实现下采样以减少空间维度。相反，转置卷积广泛用于对其输入进行空间上采样。这种功能关系导致一些研究将转置卷积视为一种反向卷积形式。然而，从数学角度来看，转置卷积不是卷积的真正逆运算；它可以通过在输入元素之间插入零，然后进行标准卷积来描述。

与反卷积（deconvolution）相关的一个显著方法是用于图像去模糊的反卷积，它通过近似模糊过程的逆运算来从模糊图像中恢复清晰图像。然而，反卷积方法通常涉及迭代优化，并且通常专门用于去模糊，限制了其作为通用神经网络模块的灵活性。

另一个密切相关的工作是可逆卷积（invertible convolution），它通过施加特定约束（如相同的输入输出形状和可处理的雅可比矩阵）来确保精确的可逆性。这些约束限制了其在深度网络中的适用性。值得注意的是，可逆卷积本质上是标准卷积的约束形式，而不是一个全新的算子。因此，开发一个真正的反向卷积算子仍然是一个开放且有价值的研究方向。

尽管有效，这些方法通常会假定一个已知的模糊核操作在单通道灰度图像或者三通道RGB图像，这也限制了他们应用在深度网络中的高维特征表征上的使用。尽管最近的深度Wiener Deconvolution可以应用到深度特征上，但是其主要针对于图像去模糊。

因此，开发一个数学上严格、计算上高效、应用上广泛的反向卷积（reverse convolution）算子具有重要的理论意义和实用价值。这种算子不仅能够实现卷积的真正逆运算，还能够在各种深度学习架构和任务中灵活应用，为深度模型设计提供新的思路和工具。

所以本文中，作者希望提出一种一次计算、无需迭代、支持任意通道维度、可直接嵌入现有网络并真正反转 depthwise convolution 的可学习算子。

研究内容

提出了一种深度可分离 reverse convolution 算子 Converse2D，用于 denoising、super-resolution、deblurring。

具体目标

给定 feature map $\mathbf{X}\in {\mathbb{R}}^{H\times W}$，使用形状为$k_h\times k_w$的depthwise卷积核 $\mathbf{K}$，按照步长 $s$ 进行卷积后得到 $\mathbf{Y}=(\mathbf{X}\otimes \mathbf{K}){\downarrow }_s$。

目标是在已知 $\mathbf{Y},\mathbf{K},s$ 时，恢复 $\mathbf{X}$，即 $\mathbf{X}=\mathcal{F}(\mathbf{Y},\mathbf{K},s)$。

优化问题

如上恢复输入的过程，可以看做是可以最小化重构输出和实际输出之间误差的近似输入。即最小化

$$\Vert \mathbf{Y}-(\mathbf{X}\otimes \mathbf{K}){\downarrow }_s{\Vert }_F^2+\lambda \Vert \mathbf{X}-{\mathbf{X}}_0{\Vert }_F^2$$

• $\lambda >0$ 为正则化参数，控制重构和正则化的权衡。在本文中，正则化参数可以在训练过程中联合优化，从而避免类似于现有大多数 deconvolution 算法中的手工调整
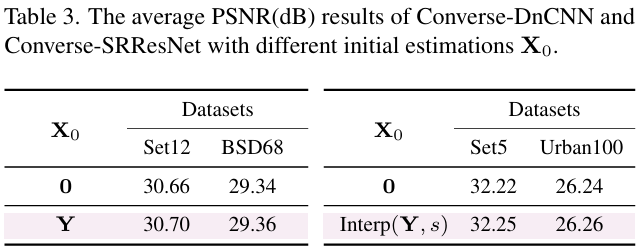
• ${\mathbf{X}}_0$ 为初始估计，可以引导求解过程朝向更稳定和可信的结果，避免对于过拟合。

这里的$\lambda \Vert \mathbf{X}-{\mathbf{X}}_0{\Vert }_F^2$是考虑到直接基于第一项的优化过程，由于退化恢复问题本身的病态特性可能导致的不稳定，而额外引入的正则化项。例如，跨步卷积的下采样过程，恰好把高频细节压到 0，于是零空间包含大量高频模式（即进过这种操作处理后会输出0的输入向量集合），从而从低分辨率输出无法唯一确定高分辨率输入，所以可以称这个逆问题是“病态”的。所以通过引入额外的正则项，将实际的解限制在合理的初始解的附近，避免病态带来的无意义的高频噪声。论文中引入了两种简单的初始估计${\mathbf{X}}_0=0$和${\mathbf{X}}_0=\text{Interp}(\mathbf{Y},s)$，后者表示对输出的上采样插值操作。

求闭式解

这里采用了循环边界假设（fast single image super-resolution using a new analytical solution for l2-l2 problems），即将二维特征图在四个边缘首尾相连后看做一个完整的环形图像，例如上边缘的上一行其实是原图的最下面一行，左边缘的左一列其实是原图的最右面一列。在数学上，任意位置的像素都可以通过取模运算对应到图像实际坐标上。这样的处理方式，把卷积变成循环卷积（circular convolution），从而可用 FFT 在频域一次性计算整幅图，推导闭式解时能得到干净的频域公式。

整体的闭式解为

$${\mathbf{X}}^{\ast }={\mathbf{F}}^{-1}\left(\frac{1}{\lambda }\left(\underset{\mathbf{L}}{\underbrace{\overline{{\mathbf{F}}_K}{\mathbf{F}}_{Y{\uparrow }_s}+\lambda {\mathbf{F}}_{X_0}}}-\overline{{\mathbf{F}}_K}{\odot }_s\frac{({\mathbf{F}}_K\mathbf{L}){\Downarrow }_s}{|{\mathbf{F}}_K{|}^2{\Downarrow }_s+\lambda }\right)\right)$$

1. $\mathbf{F}(\cdot )$ 表示 FFT，${\mathbf{F}}^{-1}(\cdot )$ 表示正逆FFT
2. $|{\mathbf{F}}_k|=\overline{{\mathbf{F}}_k}\odot {\mathbf{F}}_k$，即卷积核$\mathbf{K}$的傅里叶变换形式${\mathbf{F}}_k$的复共轭和其自身之间的元素乘积，反映了平方幅度
3. ${\mathbf{F}}_{Y{\uparrow }_s}$表示通过插入0值放大$s$倍后特征的傅里叶变换
4. ${\odot }_s$ 表示在$s\times s$个不同块上的元素乘法
5. ${\Downarrow }_s$ 为块级别下采样，即应用到$s\times s$个块之间的平均操作
6. 注意，该公式采用了${\downarrow }_s$表示从$s\times s$块中选择左上角像素的下采样形式的假设
7. 当$s=1$，该公式简化为 ${\mathbf{X}}^{\ast }={\mathbf{F}}^{-1}\left(\frac{\overline{{\mathbf{F}}_K}{\mathbf{F}}_Y+\lambda {\mathbf{F}}_{X_0}}{|{\mathbf{F}}_K{|}^2+\lambda }\right)$
8. 这里的卷积核实际上可以联合网络学习，也可以以先验的形式作为条件输入

具体实现

为了实现Converse2D，这里介绍了几个关键的组件细节：

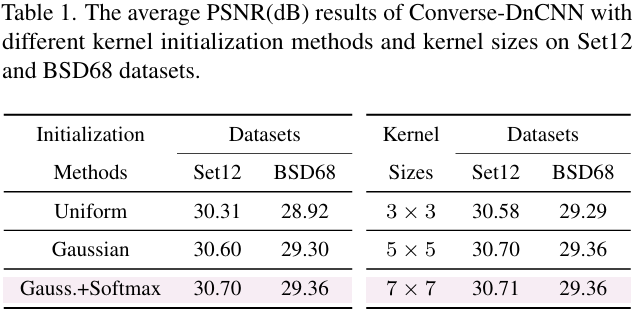
• 卷积核$\mathbf{K}$：初始化很重要，影响Converse2D生成的解的稳定性和准确性。受启发于经典的去模糊方法，本文对随机初始化的$\mathbf{K}$进一步应用 Softmax 归一化，保证非负且和为 1。在高斯去噪任务上，这一方案效果优于均匀分布和高斯分布的初始化。同时实验也展示了$5\times 5$大小的卷积核提供了更好的性能和效率的权衡。
  

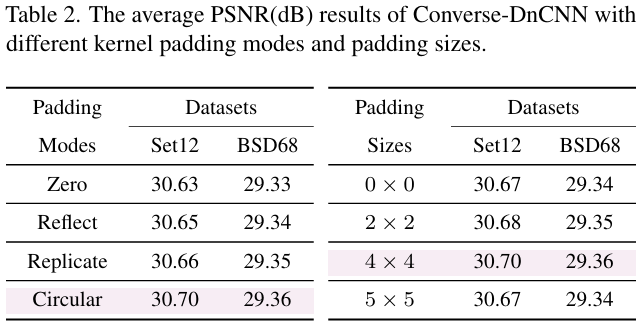
• Padding策略：这回影响边界信息的处理方式和输出的空间尺寸。因此本文在提出的Converse2D上，分析了不同的padding模式（包括circular、reflect、replicate和zero padding）和尺寸。实验中 padding size本身影响不大。circular padding 呈现了一致的优势，这与现有去模糊的文献中发现类似，因为circular padding可以更好的处理边界并减少锯齿。所以默认使用circular padding。
  

• 正则化参数：因为Converse2D本身是通道级别的应用形式，所以可以自然的为每个通道分配独立的正则化参数来处理特征统计的变化，由于正则化参数本身也被集成到了Converse2D的计算中，所以可以自然地通过学习的方式来调整。这里使用了 $\lambda =\text{Sigmoid}(b-9.0)+ϵ$ 的形式，其中$epsilon$ 是一个很小的常数来维持数值稳定。所有的可学习标量$b$被初始化为0，并在训练中自适应调整。而引入的偏移值“9”，则是用于产生一个较小的初始值，从而鼓励训练开始具有更强的数据保真度。

• 初始估计 ${\mathbf{X}}_0$：实验对比反应了 Interp$(\mathbf{Y},s)$ 优于全零初始化，这是因为插值形式提供了一个更好的近似，而全零初始化导致更慢的收敛以及降低了恢复细微结构的能力。
  

基于算法伪代码的大致实现如下：

import torch
import torch.nn.functional as F
import mathdef p2o(psf: torch.Tensor, out_shape):"""把空间核 (PSF)转成频域形式 (OTF)。卷积核之所以能被称作 PSF（Point-Spread Function），是因为在图像退化的线性系统里，卷积核恰好描述了“一个理想点光源经过该系统后所成的像”。psf: (B, C, kh, kw) PSF（Point-Spread Function） 就是空间域的卷积核 k，描述一个点光源经过系统后扩散成的“模糊斑”out_shape: (H*S, W*S) 目标高分辨率尺寸return: (B, C, H*S, W*S) OTF（Optical Transfer Function） 则是频域的表示，等于 PSF 的傅里叶变换"""B, C, kh, kw = psf.shapeH, W = out_shape# 零填充到目标尺寸pad_h = H - khpad_w = W - kwpsf_pad = F.pad(psf, (0, pad_w, 0, pad_h))          # (B,C,H,W)# 循环移位，使核中心位于 (0,0)psf_pad = torch.roll(psf_pad, shifts=(-(kh//2), -(kw//2)), dims=(-2, -1))# 转到频域otf = torch.fft.fftn(psf_pad, dim=(-2, -1))return otfdef splits(x: torch.Tensor, s: int):"""把 tensor 切成 s×s 个块x: (B, C, H*S, W*S)return: (B, C, H, W, s*s)"""B, C, HS, WS = x.shapeH = HS // sW = WS // sx = x.view(B, C, s, H, s, W)x = x.permute(0, 1, 3, 5, 2, 4).contiguous()x = x.view(B, C, H, W, s * s)return xdef sfold_upsampler(self, x: torch.Tensor, s: int):'''通过将元素复制到新的 sxs 局部区域的左上角来放大x: (B, C, H, W)return: (B, C, H*s, W*s)'''B, C, H, W = x.shapez = torch.zeros((B, C, H * s, W * s)).type_as(x)z[..., ::scale, ::scale].copy_(x)return zdef converse2d(X: torch.Tensor, K: torch.Tensor, S: int, bias: torch.Tensor) -> torch.Tensor:"""X: 输入特征图 (B, C, H, W)K: 卷积核 (B, C, kH, kW)S: 上采样/下采样比例bias: 可学习标量 (C,1,1) 用于生成 λreturn: 输出特征图 (B, C, H*S, W*S)"""B, C, H, W = X.shape# 1. 可学习的正则化参数 λlamb = torch.sigmoid(bias - 9.0) + 1e-5# 2. 最近邻上采样得到 X 的初始估计X_0 = F.interpolate(X, scale_factor=S, mode='nearest')# 3. 把输入 X 通过插零放大Y_S = sfold_upsampler(X, S)# 4. 核转到频域 OTFFK = p2o(K, (H * S, W * S)) # (B,C,H*S,W*S) 复数FK_conj = torch.conj(FK) # 取共轭FK_2 = torch.abs(FK) ** 2 # 元素级 |FK|^2# 5. 频域计算 L: B,C,H*S,W*SFKY = FK_conj * torch.fft.fftn(Y_S, dim=(-2, -1))L = FKY + torch.fft.fftn(lamb * X_0, dim=(-2, -1))# 6. 计算 FKL 与 FK2 的块均值FKL_S = splits(FK * L, S).mean(dim=-1) # (B,C,H,W)FK2_S = splits(FK_2, S).mean(dim=-1)# 7. 频域除法Fdiv = FKL_S / (FK2_S + lamb)# 8. 通过对整体的重复来恢复 Fdiv 到高分辨率Fmul = FK_conj * Fdiv.repeat(1, 1, S, S) # (B,C,H,W) -> (B,C,H*S,W*S)Fout = (L - Fmul) / lamb# 9. 逆 FFT 取实部out = torch.fft.ifftn(Fout, dim=(-2, -1)).realreturn out

模型细节

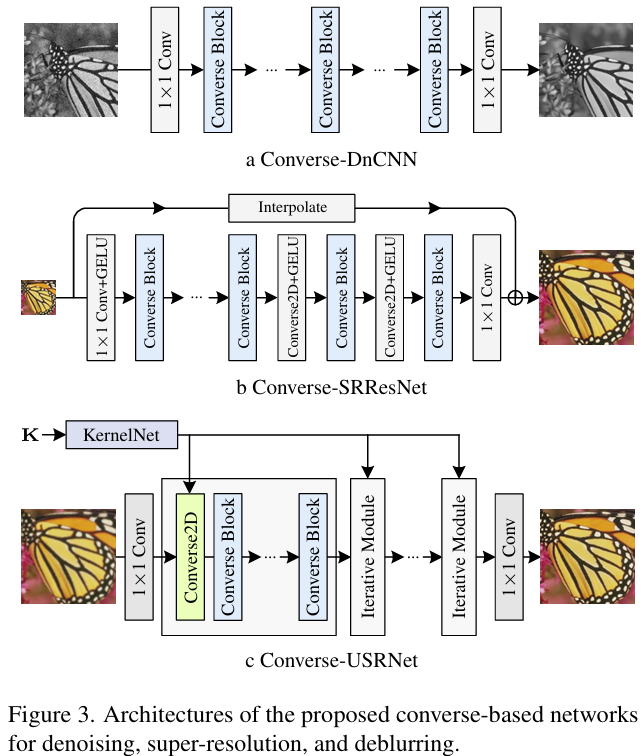
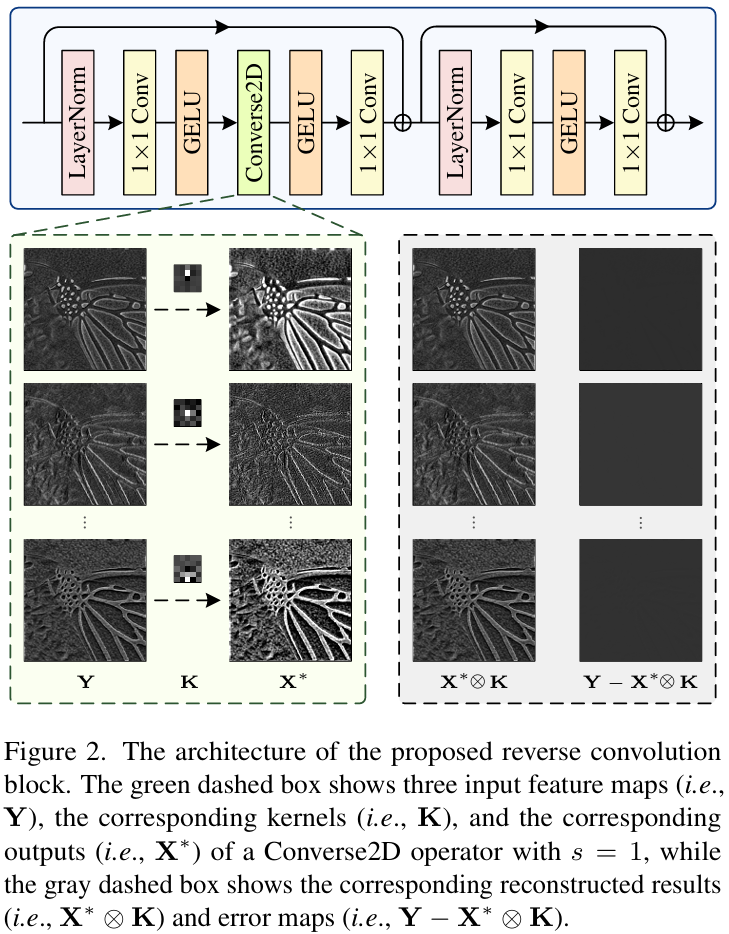
本文基于提出的 Converse2D，构建了Reverse Convolution Block，其中包含 LayerNorm、1×1 Conv、GELU、Converse2D（深度分离的形式）、残差连接，内部实现空间（主要由Converse2D负责）与通道（主要由1x1卷积处理）分离建模。

• Converse-DnCNN和Converse-SRResNet均直接替换各自的核心构建块为Converse2D算子模块
• Converse-USRNet则是用于展示所提算子在kernel-conditioned的场景中的表现，即非盲去模糊任务。将 USRNet 的 data module 换成 Converse2D、并替换其中的ResUNet denoiser为ConverseNet，这包含了7个Converse Block。也设计了 KernelNet 将模糊核映射到 64 维嵌入，这可以直接用于参数化 Converse2D，只有正则化参数是可学习的。

研究价值

首次给出 depthwise convolution 的严格可逆算子，一次前向完成反演；可直接替换现有卷积/转置卷积层，无需迭代；支持任意通道维度，可在特征域而非图像域完成 non-blind deblurring；实验显示在 denoising、super-resolution、deblurring 上均优于或与原结构持平，具有通用模块潜力。

要点汇总

1. Converse2D 算子通过正则化最小二乘问题的闭式解实现了 depthwise convolution 的真正可逆运算 频域推导给出一次性前向计算公式，无需迭代，可直接嵌入深度网络（见“Closed-form Solution”）。
2. Converse2D 支持任意通道维度，可在高维特征空间完成 deblurring，突破传统 deconvolution 仅限 1、3 通道图像的限制 文中指出“unlike deconvolution methods … our operator … supports arbitrary channel dimensions, enabling broad adaptability across network architectures”（见 Abstract 和 Sec. 3）。
3. Converse Block 采用 Transformer-like 结构，将空间建模（Converse2D）与通道交互（1×1 Conv）解耦，提高模块化与表达能力 “separation of spatial and channel-wise processing makes the Converse block an effective and flexible module”（见 Sec. 3.4）。
4. Softmax 归一化的核初始化、Circular padding、插值初始估计 ${\mathbf{X}}_0$ 与可学习正则化参数 $\lambda$ 是 Converse2D 稳定训练与性能提升的关键 实验表格显示 Softmax 初始化 PSNR 高于 Uniform/Gaussian；Circular padding 优于其他模式；Interp$(\mathbf{Y},s)$ 初始化优于全零（见 Sec. 4 和表 1–3）。

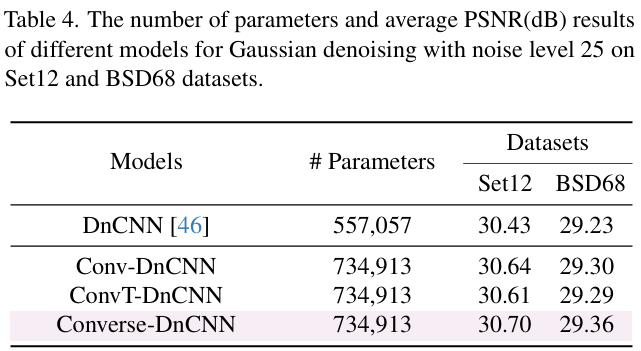
5. 在 Gaussian denoising 任务上，Converse-DnCNN 在 Set12 和 BSD68 数据集上以相同噪声水平 σ=25 取得更高 PSNR，验证算子有效性 表 4 显示 Converse-DnCNN 在 BSD68 达 29.36 dB，高于 Conv-DnCNN 与 ConvT-DnCNN。
   

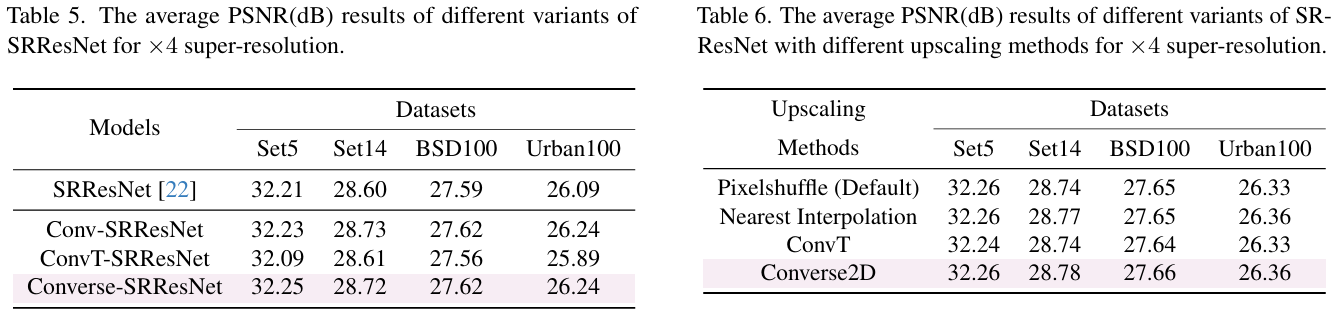
6. 在 ×4 super-resolution 任务上，Converse-SRResNet 与 SRResNet、Conv-SRResNet、ConvT-SRResNet 性能持平，证明 Converse2D 可直接替换转置卷积而不损失精度 表 5 给出各模型在 Set5/Set14/BSD100/Urban100 的 PSNR 对比。
   

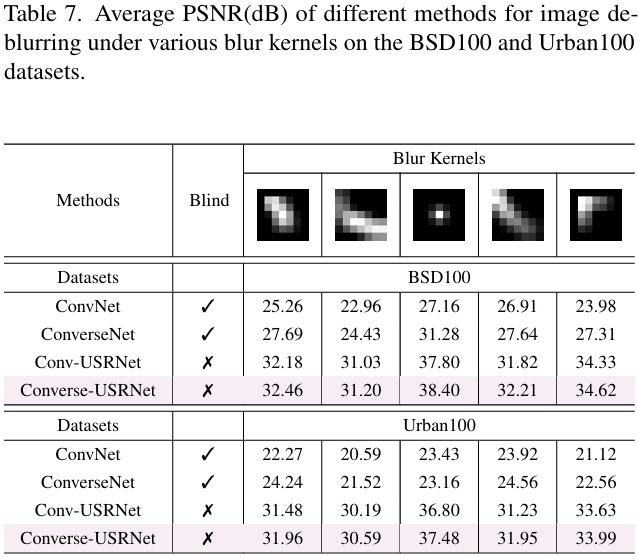
7. 在非盲 deblurring 场景下，Converse-USRNet 通过 KernelNet 将模糊核嵌入特征域，PSNR 高于 Conv-USRNet，并减少边界伪影 表 7 和图 6 对比显示 Converse-USRNet 在 BSD100/Urban100 上优于 Conv-USRNet，且“generate well-aligned and visually sharp outputs”。

8. 在盲 deblurring 设置下，ConverseNet 仍优于 ConvNet，说明 Converse2D 本身具备去卷积能力，可减轻几何失真 （见 Sec. 5.3）。

局限与扩展

论文指出目前实验采用简化设置，尚未在大规模视觉模型或更复杂退化条件下验证；未来工作将扩展到生成任务及更大规模的网络。