当前位置：首页 > news >正文

勾股数-洛谷B3845 [GESP样题二级]

news 2025/8/18 7:33:00

题目描述

勾股数是很有趣的数学概念。如果三个正整数 a,b,c，满足 a^2+b^2=c^2，而且 1≤a≤b≤c，我们就将 a,b,c 组成的三元组 (a,b,c) 称为勾股数。你能通过编程，数数有多少组勾股数，能够满足 c≤n 吗？

输入格式

输入一行，包含一个正整数 n。约定 1≤n≤1000。

输出格式

输出一行，包含一个整数 C，表示有 C 组满足条件的勾股数。

输入输出样例

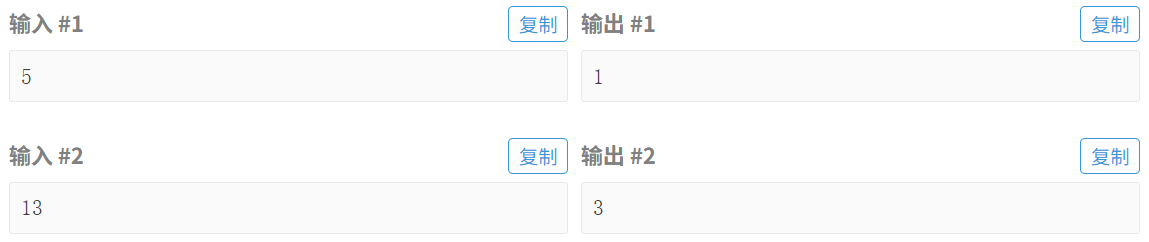
说明/提示

【样例解释 1】

满足 c≤5 的勾股数只有 (3,4,5) 一组。

【样例解释 2】

满足 c≤13 的勾股数有 3 组，即 (3,4,5)、(6,8,10) 和 (5,12,13)。

B3845 [GESP样题二级] 勾股数 - 洛谷

解题思路

对于嵌套循环类题目，考生必须具备暴力枚举和枚举优化能力，暴力能够拿部分分，只有优化才能拿满分，因此要求练习时先写出纯暴力枚举代码，再逐步优化。只有进行优化循环次数和优化循环层数的大量练习，才能确保顺利通过GESP二级考试。

参考百鸡问题

暴力枚举

根据给定的n，寻找在此范围内存在的勾股数个数，题面描述，暴力枚举公勾（a）、股（b）、弦（c)成立的个数，三层嵌套循环，无脑暴力枚举，特别注意题目描述数据范围1≤a≤b≤c。因此不必每个循环都从1开始。代码编写如下：

#include <bits/stdc++.h>
using namespace std;int main(){int n,ans=0;cin >> n;// 1≤a≤b≤cfor(int a = 1; a <= n; a++){for(int b = a; b <= n; b++){for(int c = b; c <= n; c++){if(a * a + b * b == c * c){ans++;//cout << a << " " << b << " " << c << endl;} }}}cout << ans << endl;return 0;
}

枚举层数优化

虽然我们的代码AC通过了，但是我们要养成一个习惯，三层循环尽量通过数学等量关系优化掉一层循环后，只有这样等你上考场后心态放松且自信。据此修改代码，优化掉c循环。

代码实现

#include <bits/stdc++.h>
using namespace std;
int main(){int a,b,c,n,cnt=0;cin>>n;for(int a=1;a<=n;a++){for(int b=a;b<=n;b++){c=(int)(sqrt(a*a+b*b));// 数学换算勾股数c，sqrt二级考点// 验证c的合理性if(c*c==a*a+b*b&&c<=n) cnt++;}      }cout<<cnt;return 0;
}

代码分析（注意点）

1. 遍历 b 从 a 到 n（保证 a ≤ b，避免重复计数如 (3,4,5) 和 (4,3,5)）

2. 计算 c：取 sqrt(a² + b²) 的整数部分作为 c

3. 验证条件（缺一不可）：