【深度学习3】向量化（Vectorization）

向量化（Vectorization） 是一种将数据转换为向量（或矩阵、张量）形式，并利用线性代数运算（如矩阵乘法、向量加法等）替代循环操作的技术。它是提升计算效率、简化模型实现的核心手段，尤其在处理大规模数据时至关重要。

例如在python中，c等于a（一维n个元素的数组）×b（一维n个元素的数组）可以用：

c = np.dot(a,b)#np是numpy的别名

代码速度会比用for循环快很多。

深度学习使用CPU和GPU都可以单指令流多数据流（SIMD）拥有并行的指令，只是GPU更擅长（更快）。

在可能的情况下避免使用循环，而使用向量化提升速度。

numpy中有很多向量化计算的函数：

import numpy as np
#v = [v1,v2,……,vn]
u = np。zeros((n,1))#初始化u为全0的向量
u = np.exp(v)#u等于v中各元素计算指数e^vi
u = np.log(v)#对数u = logv
u = abs(v)#绝对值
u = maximum(v,0)#计算所有元素和0之间相比的最大值
u = v**2#每个元素的平方

逻辑回归中向量化的使用

这是用循环方法写的例子，例子中有两个特征dw1和dw2，如果多的话需要用for循环处理。

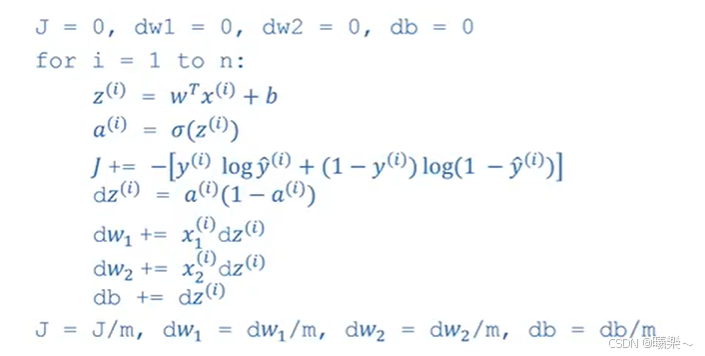
如果要去掉这个可能存在的for循环：

初始化时不用把每个dw都等于0，可以令dw = np.zeros(n-x,1)；#把所有的w放在一个dw数组中。

dw计算时，dw+=x^(i)dz^(i)

最后dw/=m

完全不使用显示for循环的逻辑回归

逻辑回归正向传播

x为单个样本，w为权重，b为偏置，z为线性的中间产物，a为经过sigmoid激活后的输出（概率）

1.计算z = wx+b

2.计算

使用numpy向量化后（把所有输入特征x放在一个X向量中）：

第一步：

Z = np.dot(w.T,X)+b

b是一个实数，但是python会自动把它扩展一个1×m的向量[b,b,……,b]，这种操作叫广播

第二步：

dz样本的预测值与实际标签的差（误差），dw为权重的梯度（更新量），db为偏置b的梯度（更新量）

dz = A-Y

db = 1/m np.sum(dZ)

dw = 1/m X dZ^T

对于外面的大for循环：

Z = np.dot(w.T,X)+b

A = sigmoid(Z)

上面那段代码不用for循环会变成下面这个样子（α是学习率）：