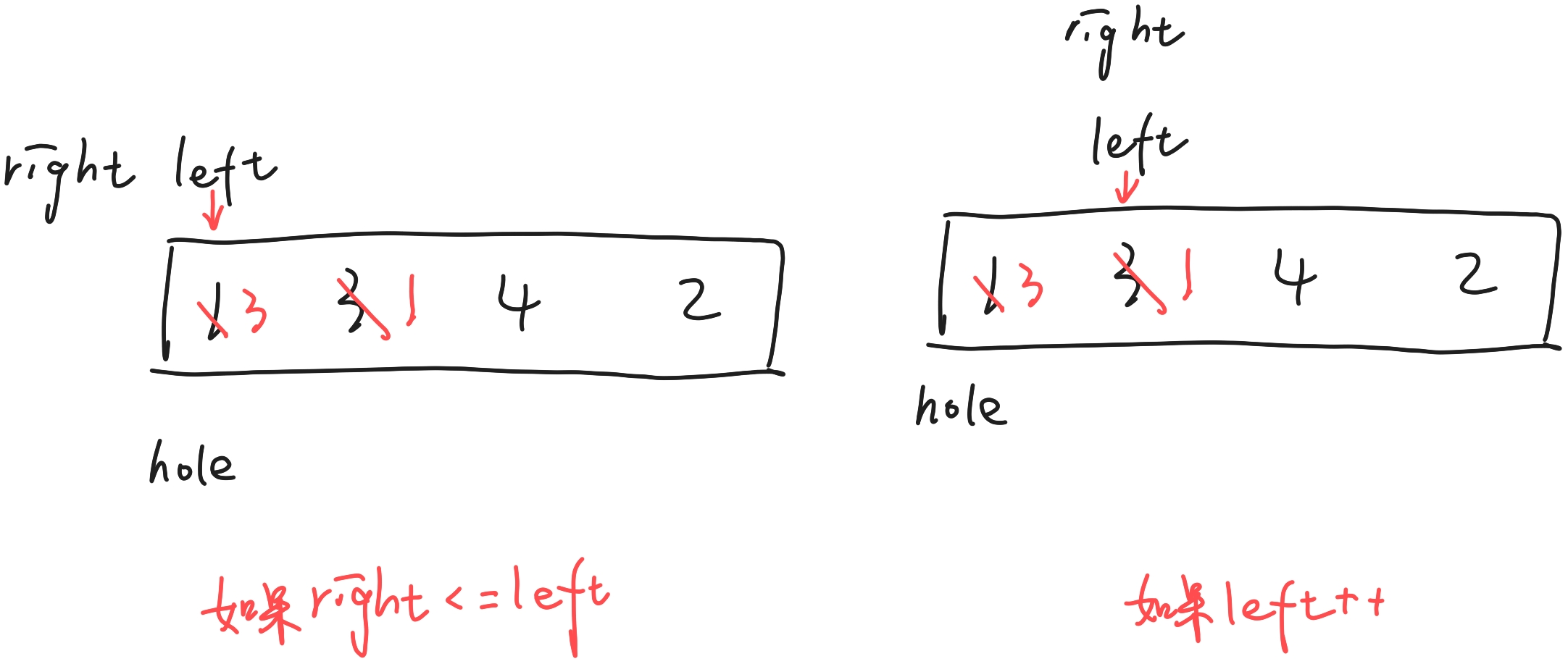初识排序(下)-- 讲解超详细
在上一节中介绍了排序的相关方法,接下来继续讲解快排和其他排序方法。
1. 快速排序
上一节讲述了交换排序中的冒泡排序,现在来介绍交换排序的快排方法。
1.1 hoare版本
看到这个名字,你会觉得这是一种很高级的方法,其实当我们了解之后,这确实是一种很牛的方法,那这个方法是怎么回事呢?我们来分析分析
快速排序是Hoare于1962年提出的⼀种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1.1.1 思路分析
有点看不懂说的是个啥,我来给你分析分析:
我们有两个探路的兵(left 和 right),left从左往右找比基准值大的,right从右往左找比基准值小的。如果找到了交换两者的值(这样做是把小的放前面,大的往后放)。
有人疑惑了,这个基准值是个啥?这个基准值就是划分左右位置的,什么意思呢?
比如划分海拔高度,有一条分界线,左侧是低于分界线海拔的集合,右侧是高于分界线海拔的集合,这里的基准值:左侧比基准值小,右侧比基准值大。我该怎么定义它呢?欸,我们在遍历找大找小的过程中就是找基准值,不妨随便先假设一个基准值,我们假设就以下标为0的为基准值。
left从左往右找比基准值大的,right从右往左找比基准值小的。如果找到了交换两者的值(这样做是把小的放前面,大的往后放)。当right<left的时候,说明右侧已经没有比基准值小的了,左侧已经没有比基准值大的了,那这个值不就是我的基准值(分界线)吗?我交换基准值和right的值。然后小的是一组,大的一组,再进行找基准值划分大小组(左右序列)。
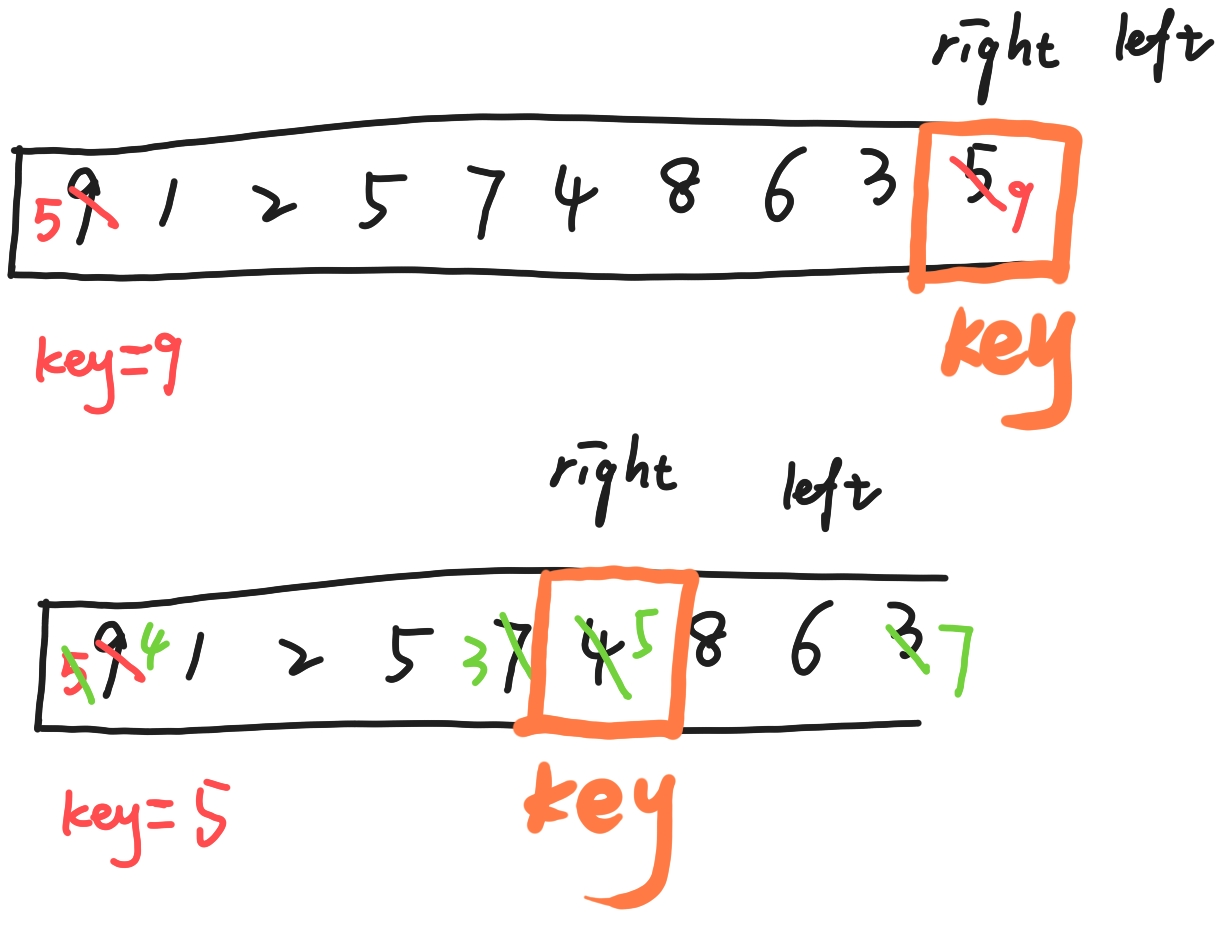
所以整体思路就清晰了:
1.假设下标为0的位置是基准值;
2.left从左往右找比基准值大的,right从右往左找比基准值小的;
3.找到了,交换两者的值,在进行一样的操作;
4.如果right < left,说明没有找到,交换right和基准值(key)的值;
5.划分左右序列,重复以上操作,直到有序。

我们不断地划分左右序列(大小组),也要分别遍历左右序列,这里就需要使用递归了,因为左序列处理完后,还需要返回处理右序列。既然要递归,就要注意递归结束的条件,当right<=left的时候就无需划分左右序列了。
1.1.2 代码实现
void QuickSort(int* arr, int left, int right)
{if(right <= left){return;}//找基准值int keyi = _QuickSort2(arr, left, right);//划分为两个序列//[left,keyi-1] keyi [keyi+1,right]QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}
//hoare版本
int _QuickSort(int* arr, int left, int right)
{int keyi = left;left++;while (left <= right){//right从右往左找比基准值大的//left从左往右找比基准值小的while (left <= right && arr[right] > arr[keyi])//要不要让arr[right] == arr[keyi],要不要交换?{right--;}//left有可能越界,left>right无需再找while (left <= right && arr[left] < arr[keyi]){left++;}if (left <= right){swap(&arr[right], &arr[left]);}}//如果left>right//交换right和keyiswap(&arr[right], &arr[keyi]);return right;
}
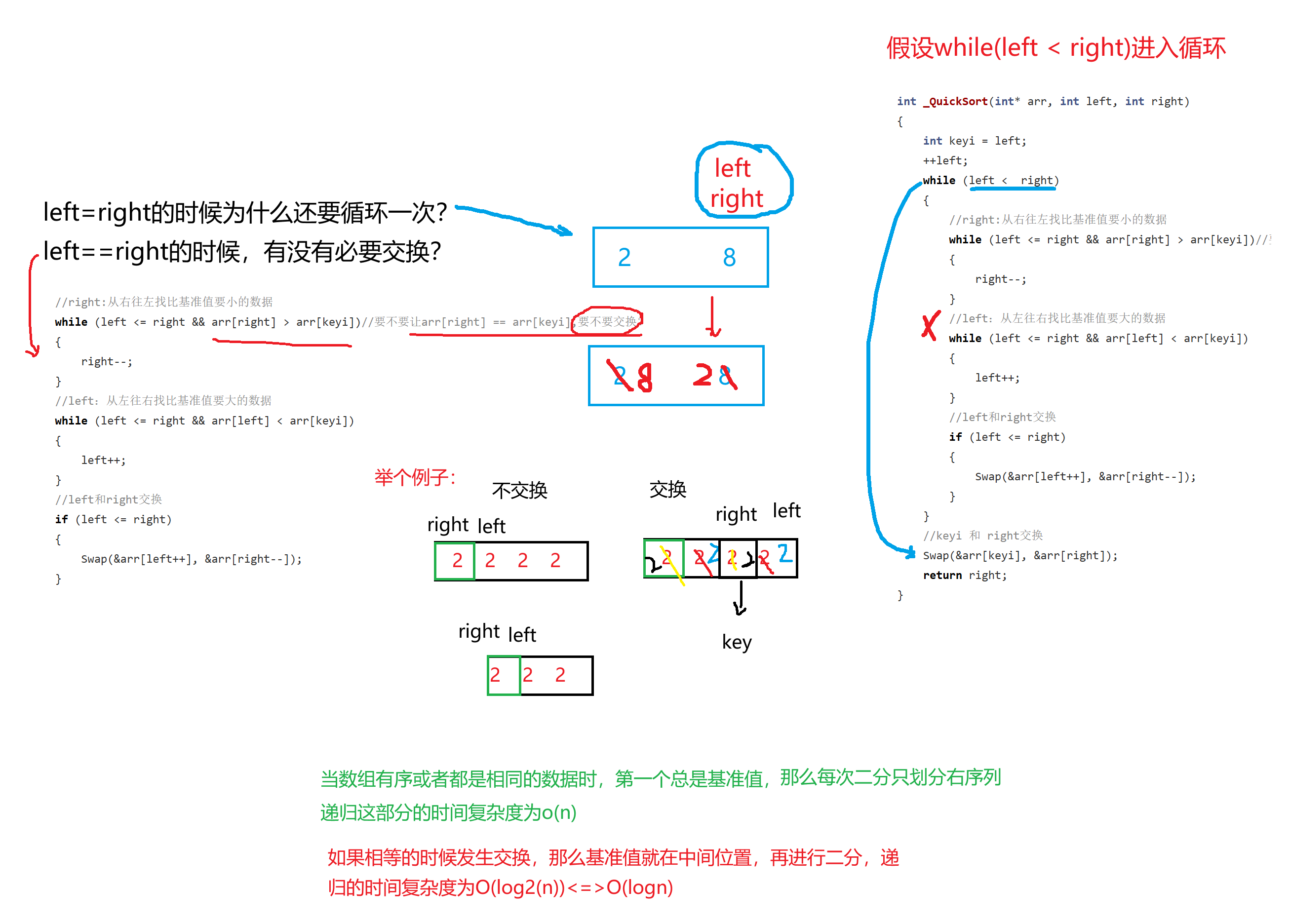
特别注意:添加left <= right是为了防止left找大时越界。

有的同学喜欢深入研究:问了几个问题:
问题1:left可不可以从下标为0的位置开始?
问题2:while(left <= right)为什么要有这个等号?
问题3:如果是while(left <= right)的条件下,当left和right相同的时候要不要交换?
解答:
问题1:如果left一开始不++,无法进入循环条件,left会一直在下标为0的位置。
问题2和问题3:如下图分析:
1.1.3 复杂度
时间复杂度:O(nlogn)
空间复杂度:O(logn)
1.2 挖坑法
挖坑法和hoare版本类似,都是一样的道理。
1.2.1 思路分析
挖坑法顾名思义就是挖一个坑,这个坑里值存放到临时变量tmp里,right从右往左找比tmp小的,left从左往右找比tmp大的,right找到了填坑,这时right的位置会形成新的坑 -- 这个坑由left来填(前提是找到了),如果left>right,就把临时变量填到坑里!!画图分析一下:
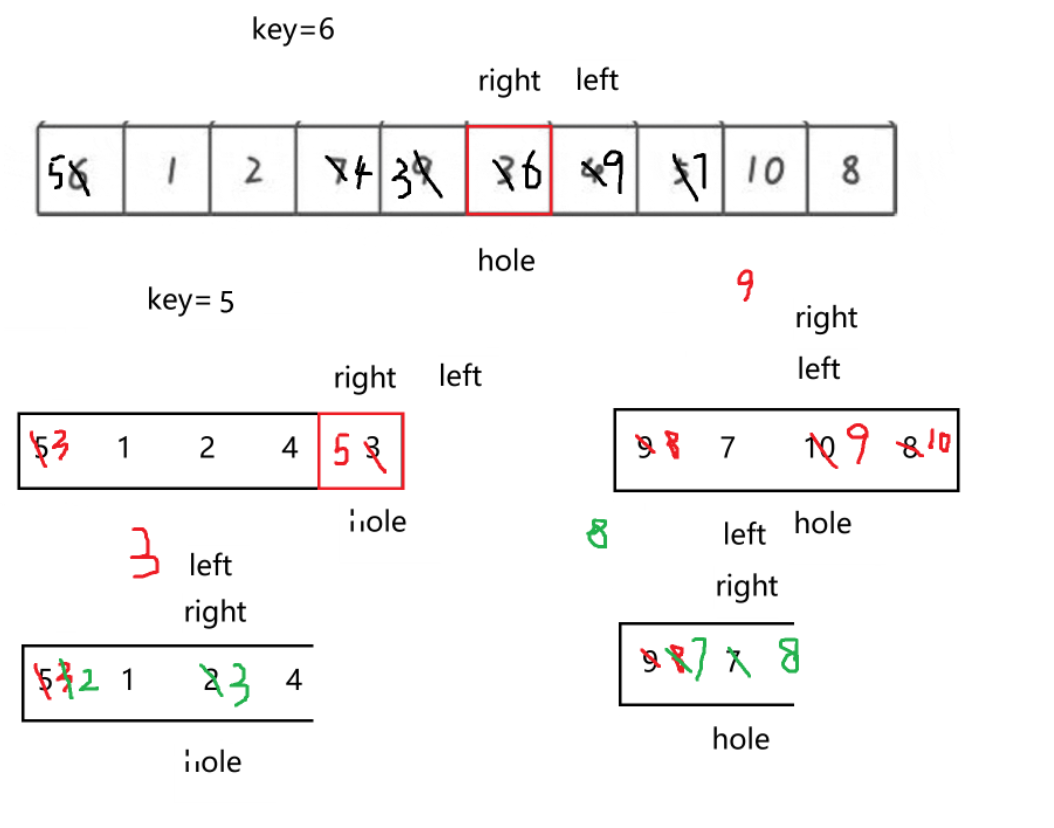
逐步分析:
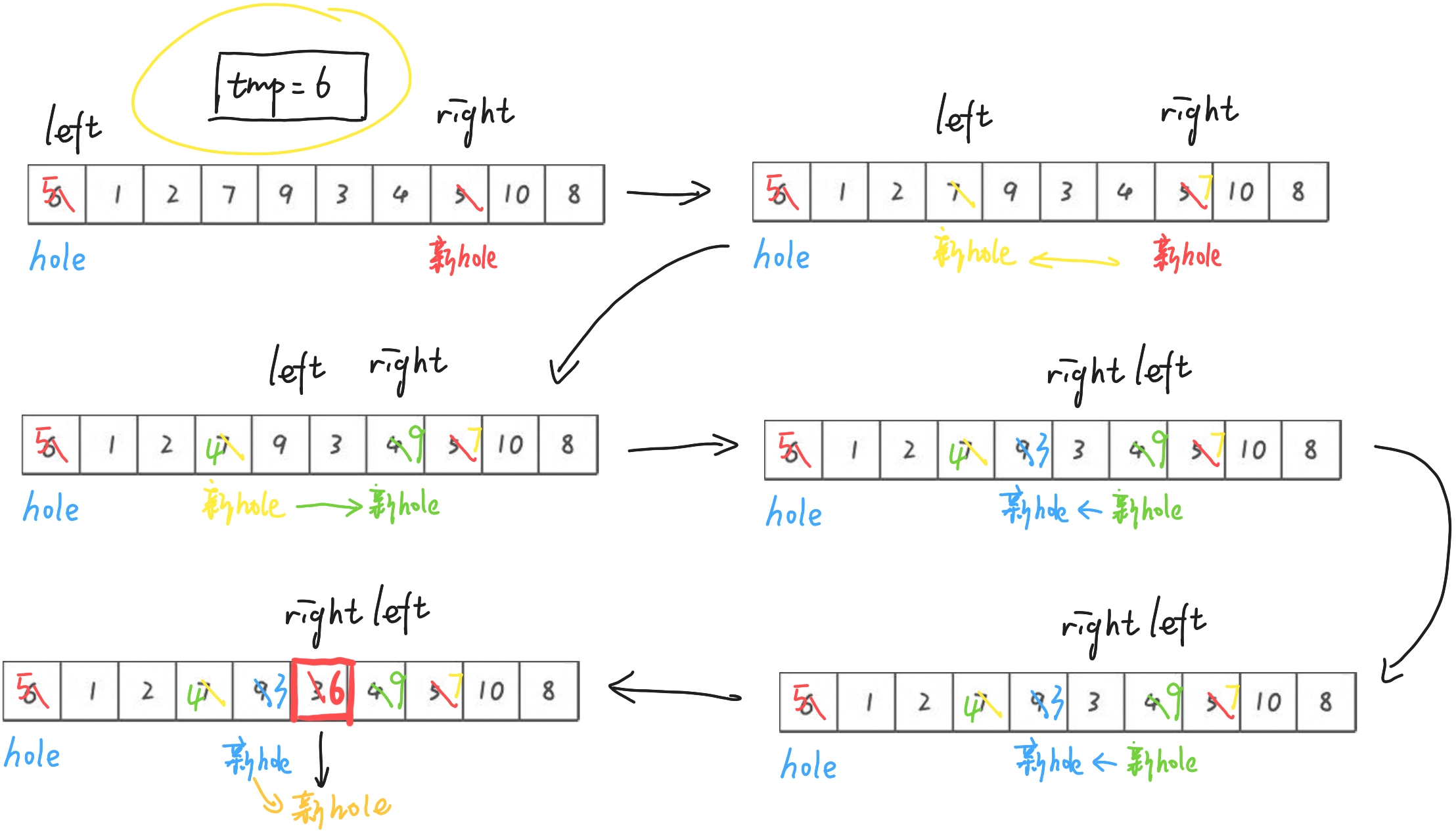
1.2.2 代码实现
//挖坑版本
int _QuickSort1(int* arr, int left, int right)
{int hole = left;int key = arr[hole];while (left < right){//right从右往左找比基准值小的while (left < right && arr[right] >= key){right--;}arr[hole] = arr[right];hole = right;//left从左往右找比基准值大的while(left < right && arr[left] <= key){left++;}arr[hole] = arr[left];hole = left;}//left>rightarr[hole] = key;return hole;
}问题:
1.这里的left为什么不能++?
2.第一个while循环为什么没有等号?(left不++)
3.为什么是arr[right] >= key 和 arr[left] <= key?前面都没有等号,为啥这里要有?
解答:
1.如果left++,会导致图右侧的结果,不符合实际预期;
2.没有等号是为了防止越界(因为第一个while循环的条件也是right和left判定的条件之一);
3.如果没有等号,给你一组含有重复值得数据:
4.如果left++,并且while有等号,结果会不会一样?你可以下来试一试
1.2.3 复杂度
时间复杂度:O(nlogn)
空间复杂度:O(logn)
1.3 lomuto前后指针
1.3.1 思路分析
思路分析:有一个指针(cur)是探路的,另一个指针(prev)待命;如果找到比基准值小的,prev++,prev和cur交换;如果没有找到,cur++,重复此过程,直到cur越界,交换prev和keyi即可
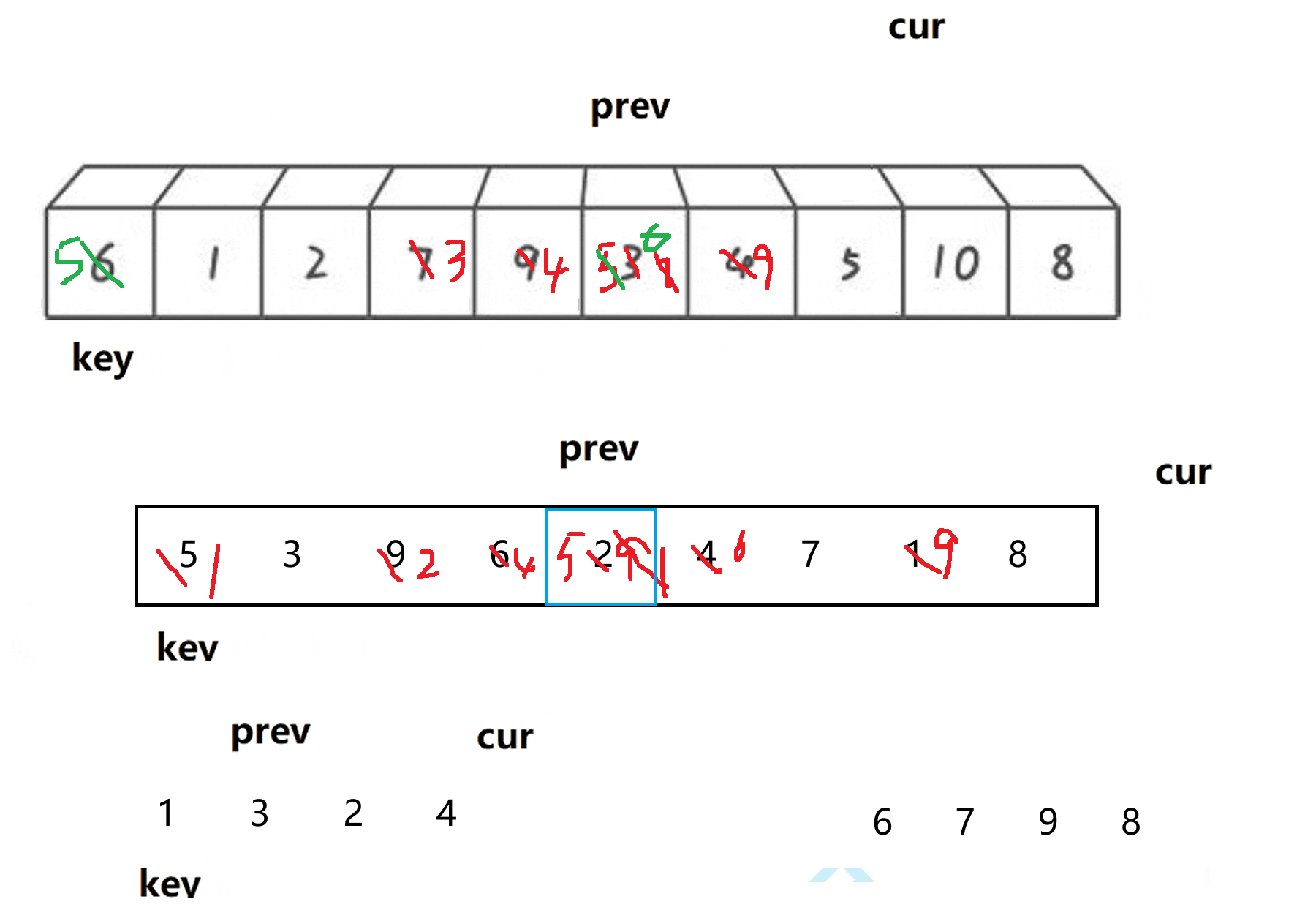
1.3.2 代码实现
//lomoto前后指针版本
int _QuickSort2(int* arr, int left, int right)
{int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){//cur找比基准值小的while (cur<=right && arr[cur] >= arr[keyi]){cur++;}if (cur <= right){prev++;swap(&arr[prev], &arr[cur]);cur++;}}swap(&arr[prev], &arr[keyi]);return keyi;
}上面分析的时候,你会发现当prev和cur在相同的位置时,可以不用交换,这里可以优化。
优化版本:
int _QuickSort2(int* arr, int left, int right)
{int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){//cur找比基准值小的if (arr[cur] < arr[keyi] && ++prev != cur){swap(&arr[prev], &arr[cur]);cur++;}cur++;}swap(&arr[prev], &arr[keyi]);return keyi;
}
1.3.3 复杂度
时间复杂度:O(nlogn)
空间复杂度:O(logn)
到这里三种快排方法就结束了,这三种排序我们都借助了递归的方法,那有没有不用递归方法就能实现呢?有的有的同学,下面就来介绍非递归版本的快排!
1.4 非递归版本
这里我们不用递归方法实现,使用其他方法,想啊想啊,想不出来该怎么实现?
我来告诉你,我们需要借助数据结构 -- 栈来实现。
1.4.1 思路分析
我们知道栈具有先入后出的特性,回顾上面划分左右序列,我们划分完之后,都是先处理左序列,处理完之后再处理右序列,那如果用栈来实现的话,就要让右序列先入栈,在入左序列。
欸,入栈入栈,是入数据吗? -- 不是,如果入数据的话,处理过程会很复杂,这里我们入左右序列的下标,根据下标来找到的对应的序列。
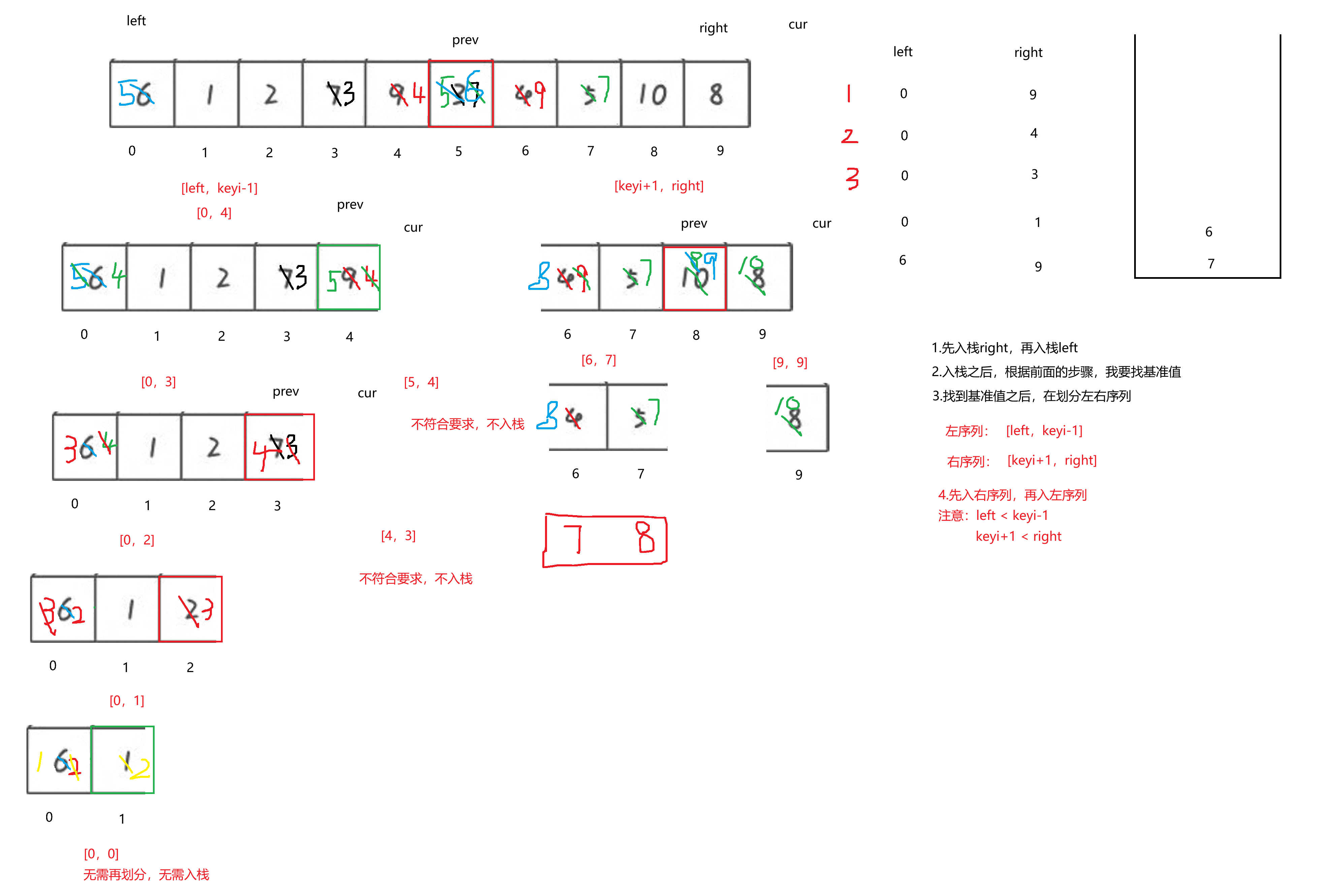
注意:整个过程中left和right都没有发生改变,所以需要有临时变量来保存,并且要保证序列是有效的!
1.4.2 代码实现
//非递归版本--快速排序
void QuickSortNorR(int* arr, int left, int right)//
{ST st;StackInit(&st);//将左右下标入栈StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)){//取栈顶元素,出栈顶int begin = Stacktop(&st);StackPop(&st);int end = Stacktop(&st);StackPop(&st);//找基准值int prev = begin;int cur = prev + 1;int keyi = begin;while (cur <= end)//(这里不能是right,right没有变化,可能越界){if (arr[cur] < arr[keyi] && ++prev != cur){swap(&arr[prev], &arr[cur]);}cur++;}swap(&arr[prev], &arr[keyi]);keyi = prev;//划分左右序列//左序列 [begin,keyi-1]//右序列 [keyi+1,end]if (keyi + 1 < end){StackPush(&st, end);StackPush(&st, keyi + 1);}if (begin < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, begin);}}StackDestroy(&st);
}这就是非递归版本的快排,只要理解了思路写起来就不会那么难了!!!
2. 归并排序
归并排序算法思想: 归并排序(MERGE-SORT)是建立在归并操作上的⼀种有效的排序算法,该算法是采用分治法(Divide andConquer)的⼀个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
2.1 思路分析
什么意思呢?我们先来看一张图:
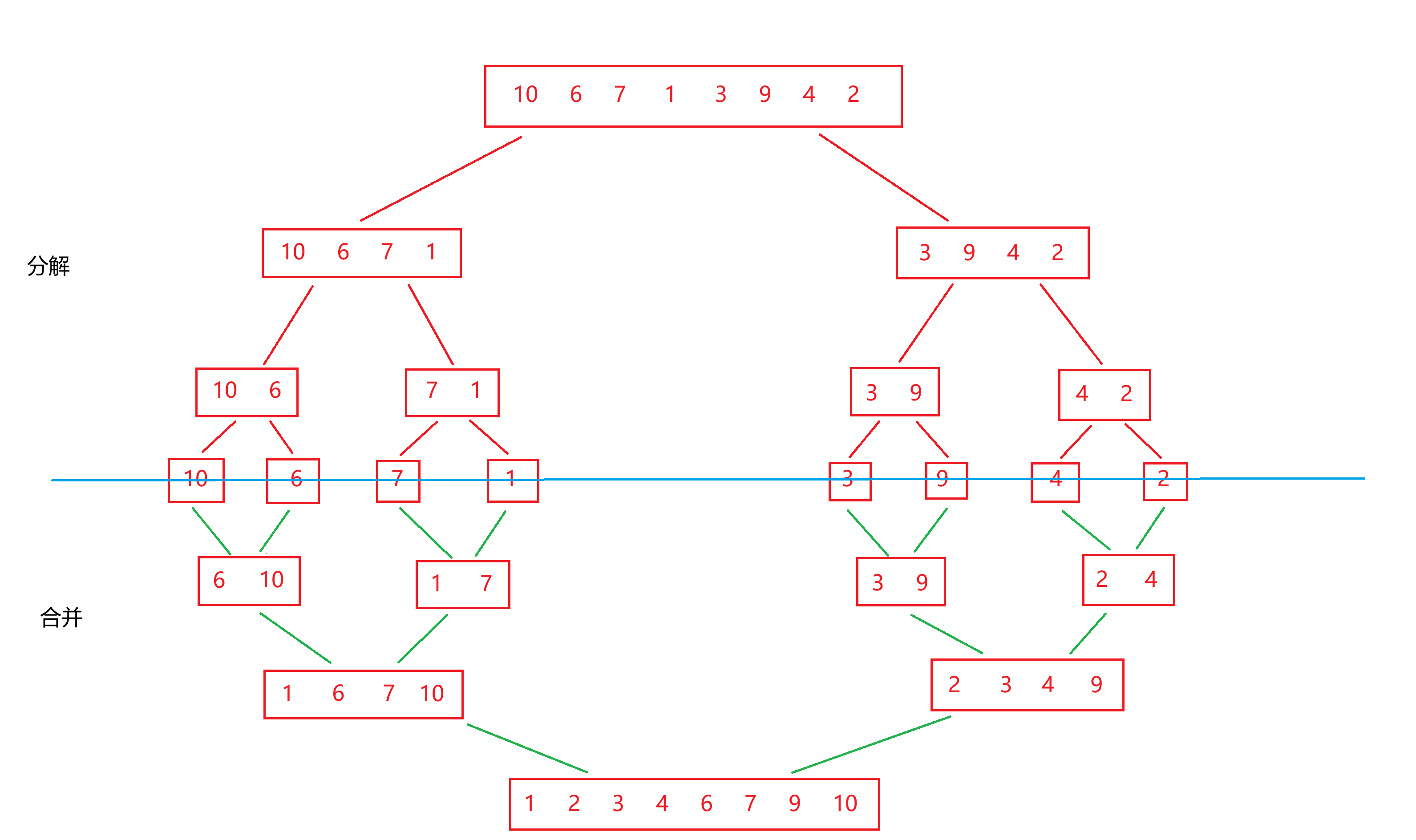
根据图来分析,我们要把数据二分直到不能再二分,为什么这样做呢?(定义的)
如何进行二分呢?二分的话就得找到中间值mid,mid=(left+right)/2;
找到中间值之后,进行二分,左序列:[left,mid];右序列:[mid+1,right]
二分结束的条件是什么呢? -----> left>=right,这个时候只剩下一个元素,没必要再二分。
---------------------------------------------------------------------------------------------------------------------------------
二分之后,我们要进行归并,什么意思呢?就是相邻两组数据进行大小比较,比较的结果存放到临时数组,直到每个数据比较完毕。
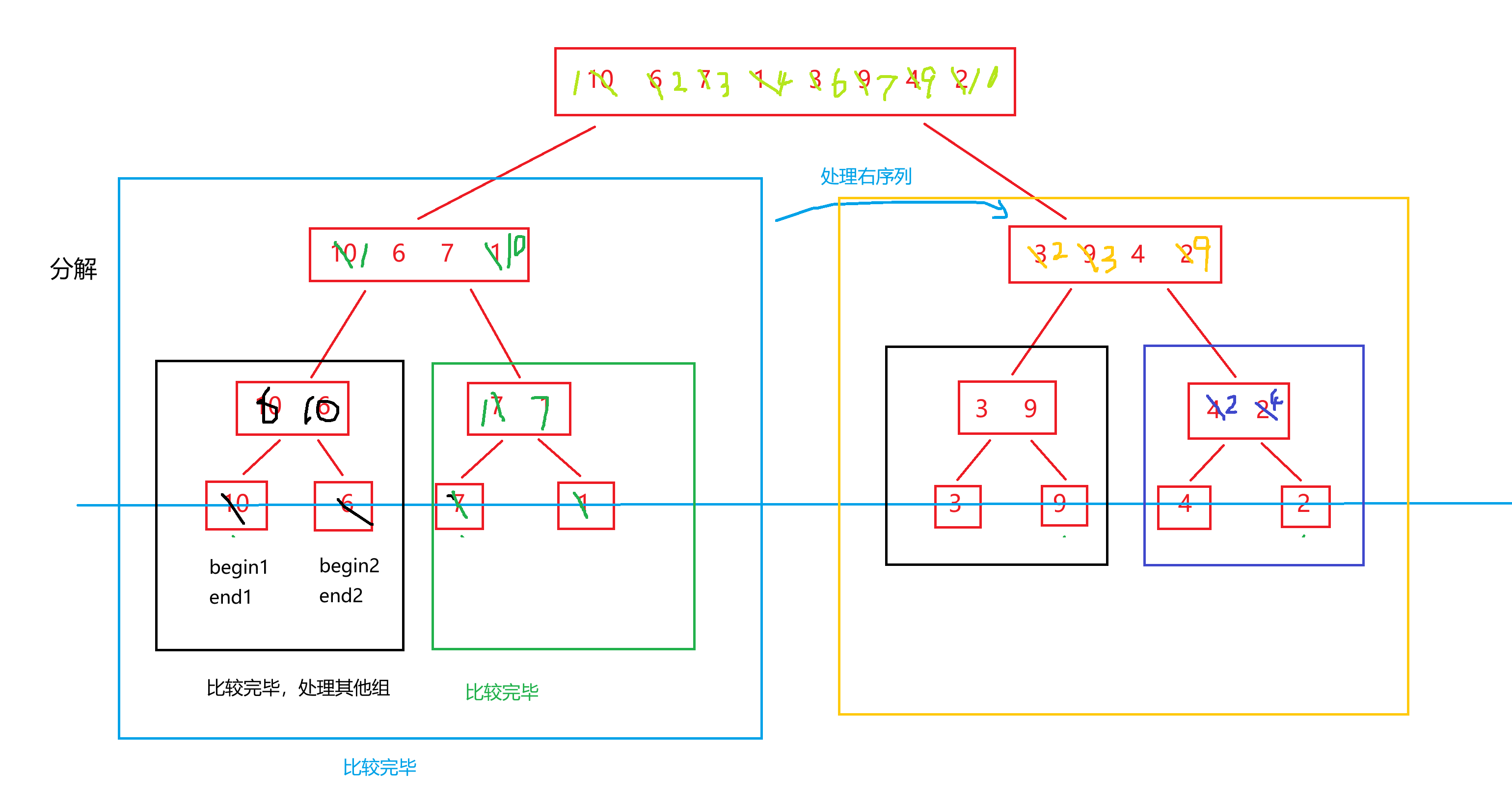
左边递归完,才处理右边部分!!!
思路清晰了,我们直接上代码!
2.2 代码实现
void _MerMergeSort(int* arr, int left, int right, int* tmp)
{//二分if (left >= right){return;}int mid = (left + right) / 2;_MerMergeSort(arr, left, mid, tmp);_MerMergeSort(arr, mid + 1, right, tmp);//比较大小//左序列int begin1 = left;int end1 = mid;//右序列int begin2 = mid + 1;int end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}//比较完之后,可能还有数据没有比较while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//将排序后的数据,重新存放到arr数组for (int i = left; i <= right; i++){arr[i] = tmp[i];}//注意这里不能这样写,因为begin1在不断的变化!!!//for (int i = begin1; i <= end2; i++)//{//arr[i] = tmp[i];//}
}void MergeSort(int* arr, int left, int right)
{int* tmp = (int*)malloc(sizeof(int) * (right));_MerMergeSort(arr, left, right, tmp);
}2.3 复杂度
时间复杂度:O(nlogn)
空间复杂度:O(n)
3. 排序性能对比
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();//执行到这里的时间InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);//排序的时间printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}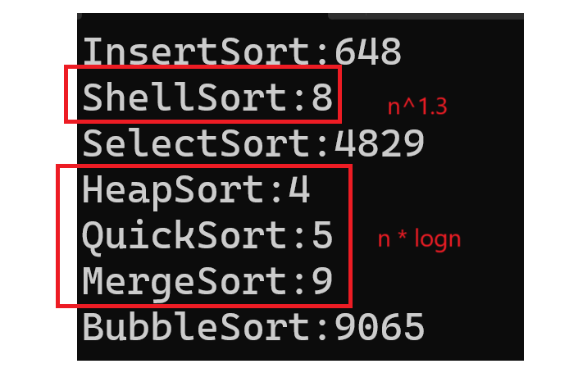
根据时间,会发现堆排序是最好的,冒泡排序是最差的。
那么到这里排序就已经结束了,下一次将会进入C++阶段了!!!敬请期待~