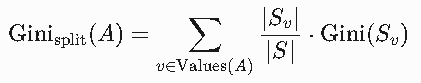机器学习 入门——决策树分类
决策树是一种直观且强大的机器学习算法,适用于分类和回归任务。本文将全面介绍决策树分类的原理、实现、调优和实际应用。
一、什么是决策树分类
1.概念
决策树分类是一种树形结构的分类模型,它通过递归地将数据集分割成更小的子集来构建决策规则。就像我们日常生活中做决策一样(例如:如果天气晴朗,就去公园;否则在家看电影),决策树通过一系列的判断条件来对数据进行分类。下图为一个决策树
2.构建过程
特征选择:
使用指标(如信息增益、增益率或基尼指数)选择最佳分裂特征。
信息增益(ID3算法):选择使信息熵下降最多的特征。
增益率(C4.5算法):解决信息增益对多值特征的偏好问题。
基尼指数(CART算法):衡量数据不纯度,值越小纯度越高。
节点分裂:
根据特征的阈值(连续值)或类别(离散值)将数据划分为子集。
递归处理子集,直到满足停止条件。
剪枝策略(防止过拟合):
预剪枝:在分裂前评估,若增益不足则停止分裂。
后剪枝:先构建完整树,再自底向上剪去不重要的分支。
二、决策树的分类标准
1、信息增益(Information Gain)
1. 核心概念
(1)熵(Entropy)
定义:衡量数据集的不确定性(混乱程度)。熵越大,数据越无序。
公式:
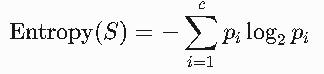
S:当前数据集;
pi:类别 i在数据集中的比例;
c:类别总数。
例子:
若数据集全是同一类别(如全为“是”),熵为0(完全确定)。
若类别均匀分布(如“是”“否”各占50%),熵为1(最大不确定性)。
天气 | 温度 | 湿度 | 风力 | 是否出去玩 |
|---|---|---|---|---|
晴 | 高 | 高 | 无 | 否 |
晴 | 高 | 高 | 有 | 否 |
多云 | 高 | 高 | 无 | 是 |
雨 | 中 | 高 | 无 | 是 |
雨 | 低 | 正常 | 无 | 是 |
上述列表中类别分布为3个“是”,2个“否”。
所以信息熵为
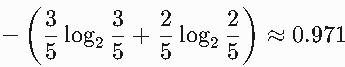
(2)信息增益(Information Gain)
定义:划分前后熵的减少量,反映属性对分类的贡献。
公式:
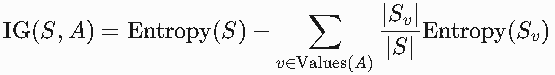
A:候选属性;
Values(A):属性 A的所有可能取值;
Sv:属性 A取值为 v的子集。
目标:选择使 IG(S,A)最大的属性 A。
对于上述数据,可以计算出每个属性的信息增益以天气为例
取值:晴(2条)、多云(1条)、雨(2条)。
子集熵计算:
晴:2条全为“否” → Entropy(S晴)=0。
多云:1条全为“是” → Entropy(S多云)=0。
雨:2条全为“是” → Entropy(S雨)=0。
信息增益:
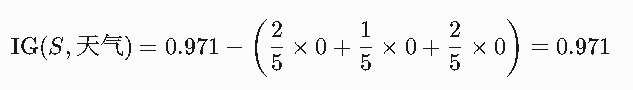 (同理可计算其他属性的信息增益,选择最大的作为划分节点。)
(同理可计算其他属性的信息增益,选择最大的作为划分节点。)
2. 构建决策树
通过计算信息增益我们就可以构建决策树。
根节点划分(天气)
天气 = 晴:2条数据,全为“否” → 叶节点(否)。
天气 = 多云:1条数据,全为“是” → 叶节点(是)。
天气 = 雨:2条数据,全为“是” → 叶节点(是)。
此时决策树已完全分类,无需进一步划分(所有子集纯度100%)。
但若假设“雨”的子集不纯(例如有“否”),则需继续划分其他属性。
2、信息增益比
信息增益比是对信息增益的改进,用于解决信息增益对多值属性的偏好问题。
通过引入属性的固有值(Intrinsic Value),惩罚取值较多的属性,从而平衡划分标准。
公式:
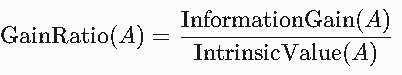
其中:
IntrinsicValue(A)=
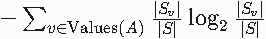
Values(A):属性 A的所有取值,Sv是取值为 v的子集。
InformationGain(A)为a属性的信息增益
计算步骤(示例)
沿用之前的天气数据集,但假设“湿度”有更多取值以演示效果:
天气 | 湿度(新) | 是否出去玩 |
|---|---|---|
晴 | 80% | 否 |
晴 | 85% | 否 |
多云 | 90% | 是 |
雨 | 75% | 是 |
雨 | 60% | 是 |
Step 1: 计算信息增益(IG)
对属性“湿度”(连续属性需离散化,假设分为高/正常):
高(80%, 85%, 90%, 75%):3否,1是 → 熵 ≈ 0.811
正常(60%):1是 → 熵 = 0
IG(湿度)=0.971−(54×0.811+51×0)≈0.322
Step 2: 计算固有值(IV)
湿度取值分布:高(4条)、正常(1条)。
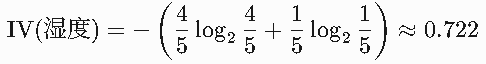
Step 3: 计算增益比
GainRatio(湿度)=0.7220.322≈0.446
3、GINI系数
基尼系数是决策树(如CART算法)中用于衡量数据不纯度的指标,表示从数据集中随机抽取两个样本,其类别标签不一致的概率。
GINI系数
公式:
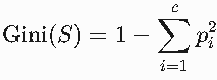
S:当前数据集;
pi:类别 i在数据集中的比例;
c:类别总数。
范围:0(完全纯净)到 0.5(均匀分布的两类)
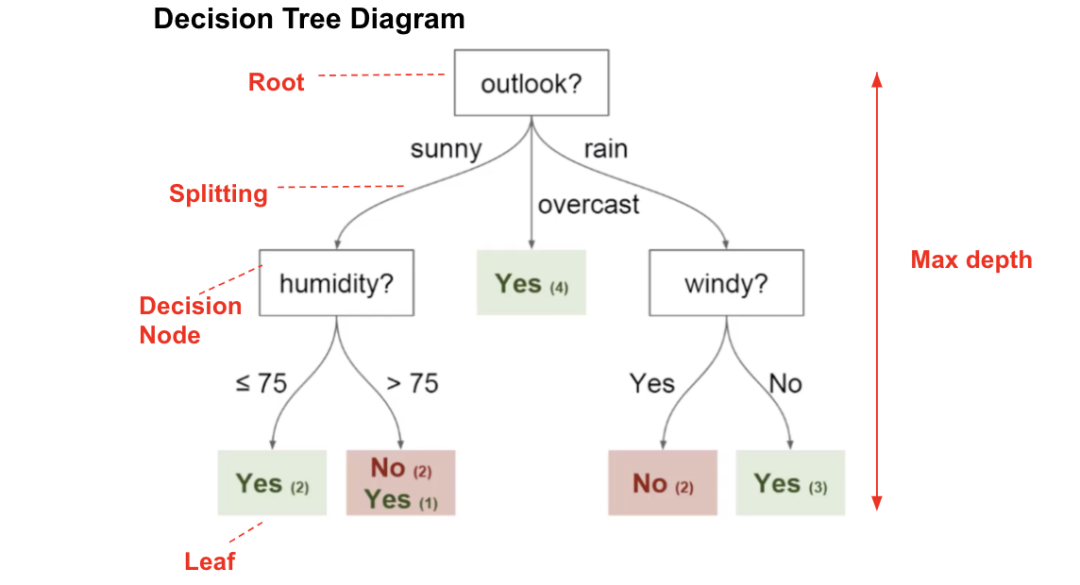
特征A条件下的加权基尼系数
公式:
Values(A):特征A的所有可能取值(如“天气”取值为晴、雨、多云)。
Sv:特征A取值为 v的子数据集。
S:特征A的数据集数
Gini(Sv):子集 Sv的基尼系数。
假设银行根据以下特征决定是否批准贷款申请:
年龄 | 收入 | 学历 | 是否有房产 | 是否批准贷款 |
|---|---|---|---|---|
青年 | 低 | 高中 | 无 | 否 |
青年 | 低 | 高中 | 有 | 否 |
青年 | 中 | 本科 | 无 | 否 |
中年 | 高 | 本科 | 有 | 是 |
中年 | 中 | 硕士 | 无 | 是 |
老年 | 中 | 硕士 | 有 | 是 |
目标:预测“是否批准贷款”
特征:年龄、收入、学历、是否有房产
Step 1: 计算初始基尼系数
类别分布:3“否”,3“是”。
初始基尼系数:
Gini(S)=1−((63)2+(63)2)=1−(0.25+0.25)=0.5
Step 2: 计算各特征的基尼增益
(1)特征:年龄
取值:青年(3条)、中年(2条)、老年(1条)。
子集基尼系数:
青年:3条(全“否”)→ Gini=1−(1^2+0^2)=0
中年:2条(1“否”,1“是”)→ Gini=1−(0.5^2+0.5^2)=0.5
老年:1条(全“是”)→ Gini=0
加权基尼系数:
Ginisplit(年龄)=1/2×0+62×0.5+1/6×0≈0.167
(2)特征:是否有房产
取值:有(3条)、无(3条)。
子集基尼系数:
有:3条(1“否”,2“是”)→ Gini=1−(3/1)^2−(3/2)^2≈0.444
无:3条(2“否”,1“是”)→ Gini≈0.444
加权基尼系数:
Ginisplit(房产)=1/2×0.444+1/2×0.444≈0.444
4、决策树剪枝(Pruning)
1. 剪枝的目的
决策树容易过拟合(Overfitting),当你的数据量过大时,会导致树深度过大或节点过多。剪枝通过移除部分分支或子树,简化模型结构,提升泛化能力(指模型在未见过的数据上表现良好的能力,即从训练数据中学到的规律能否推广到新样本。)。
核心目标:在训练集准确性和测试集泛化性之间取得平衡。
2. 剪枝方法分类
(1)预剪枝(Pre-Pruning)
在决策树构建过程中提前停止生长,通过设定阈值限制树的复杂度。
预剪枝就像给树苗修剪枝叶,在决策树生长过程中提前阻止不必要的分支。通过设定规则限制树的复杂度,防止它长得"太茂盛"(过拟合)。
预剪枝的常见方法
(1) 限制树的高度(max_depth)
作用:控制树的最大层数,避免决策规则过于复杂。
例子:贷款审批时,最多只问3个问题(如年龄→收入→房产),再多就拒绝(防止过度追问隐私)。
(2) 设置节点最小样本数(min_samples_split)
作用:节点至少需要多少样本才允许继续分裂。
例子:医生诊断时,至少要有10个相似病例才新增检查项,否则按经验开药。
(3) 信息增益阈值(min_impurity_decrease)
作用:只有分裂能显著提升分类效果时才允许分裂。
例子:挑西瓜时,如果"听声音"和"看颜色"判断效果差不多,就只用其中一个特征。
三、python实战
1.sklearn.tree.DecisionTreeClassifier()参数
sklearn.tree.DecisionTreeClassifier(criterion="gini", splitter="best", max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0,)
DecisionTreeClassifier是 scikit-learn 提供的分类决策树模型,适用于离散类别预测(如垃圾邮件分类、疾病诊断)。
1.核心分裂参数
参数 | 说明 | 推荐值 | 引用 |
|---|---|---|---|
| 分裂质量评估标准: | 高维数据用 | |
| 分裂策略: | 小数据用 |
2. 剪枝与复杂度控制
参数 | 说明 | 推荐值 | 引用 |
|---|---|---|---|
| 树的最大深度。 | 通常设为 3-10,通过交叉验证选择 | |
| 节点继续分裂的最小样本数: | 样本量大时建议 ≥10 或 0.01-0.1 | |
| 叶节点最小样本数,防止噪声干扰 | 分类任务建议 ≥5 | |
| 限制叶节点总数,优先于 | 特征多时设为 10-100 | |
| 分裂需达到的最小不纯度减少量 | 0-0.1,值越大树越简单 |
3. 特征与随机性控制
参数 | 说明 | 推荐值 | 引用 |
|---|---|---|---|
| 分裂时考虑的最大特征数: | 高维数据用 | |
| 随机种子,保证结果可复现 | 固定值如 |
4. 类别不平衡处理
参数 | 说明 | 推荐值 | 引用 |
|---|---|---|---|
| 类别权重: | 类别不平衡时用 |
5. 其他实用参数
参数 | 说明 | 推荐值 | 引用 |
|---|---|---|---|
| 代价复杂度剪枝参数,后剪枝强度 | 通过交叉验证选择 | |
| 预排序数据以加速训练(已弃用) | 不推荐使用 |
2.实例——客户历史流失数据
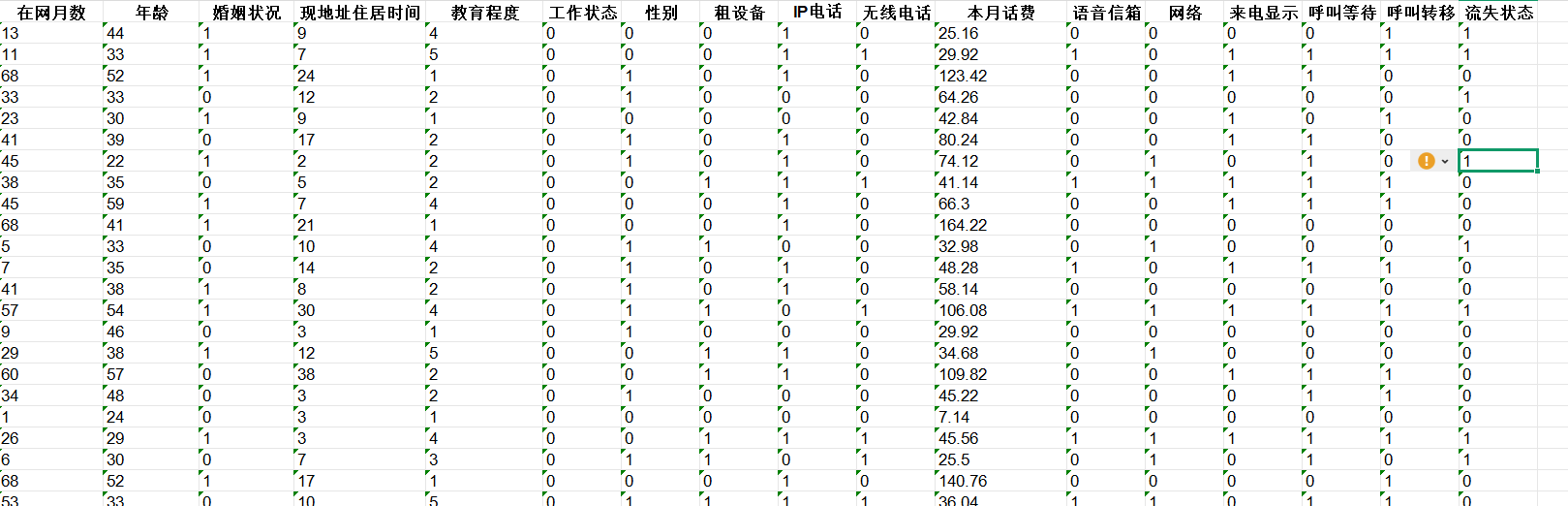
对于600多条数据,一共20个属性,两种状态,为二分类问题
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split as trtesp
#sklearn自带的拆分数据集的函数train_test_split
#导入需要用到的库data = pd.read_excel('电信客户流失数据.xlsx')x = data.iloc[:, :-1]
y = data.iloc[:, -1]x_train,x_test,y_train,y_test = \trtesp(x, y, test_size=0.2, random_state=100)#拆分数据集lr = DecisionTreeClassifier()
lr.fit(x_train, y_train)from sklearn.model_selection import cross_val_score#导入打印召回率的函数
#定义循环列表定义最大深度,分裂的最小样本,叶节点最小样本数,最大叶子节点总数范围
max_depth = [i for i in range(4,13)]
min_samples_split = [i for i in range(2,10)]
min_samples_leaf = [i for i in range(12,19)]
max_leaf_nodes = [i for i in range(9,16)]scores = 0
best = []#定义最佳参数存放列表#利用循环嵌套寻找最佳参数
for depth in max_depth:for min_samples in min_samples_split:for min_leaf in min_samples_leaf:for max_leaf in max_leaf_nodes:lr = DecisionTreeClassifier(criterion='gini',max_depth=depth,min_samples_split=min_samples,min_samples_leaf=min_leaf,max_leaf_nodes=max_leaf,random_state=42)#进行交叉验证,评估模型的泛化能力score = /cross_val_score(lr, x_train, y_train, cv=8,scoring='recall')scores_m = sum(score)/len(score)#计算分数if scores_m > scores:#统计最大分数scores= scores_mbest = [depth,min_samples,min_leaf,max_leaf]print('最佳惩罚因子为:',best[:])
#训练最佳参数模型
lr = DecisionTreeClassifier(criterion='gini',max_depth=best[0],min_samples_split=best[1],min_samples_leaf=best[2],max_leaf_nodes=best[3],random_state=42)
lr.fit(x_train, y_train)
y_spred = lr.predict(x_train)
y_pred = lr.predict(x_test)
from sklearn import metrics
print('自测:',metrics.classification_report(y_train, y_spred))#获取自测报告
print('测试:',metrics.classification_report(y_test, y_pred))#获得测试集测试报告#输出决策树图像
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
fig,ax = plt.subplots(figsize=(10,10))
plot_tree(lr,filled=True,ax=ax)
plt.show()