曼哈顿距离与切比雪夫距离
一、引入
在一座繁华而古老的城市中,发生了一起神秘的珠宝盗窃案。警方迅速展开调查,锁定了几个嫌疑人,但他们都有不在场证明,案件陷入了僵局。
负责此案的侦探林探长是个数学高手,他深知在城市的大街小巷中,隐藏着破解谜题的线索。城市的布局就像一个巨大的坐标系,每个地点都有其独特的坐标。
有一天,林探长在研究监控录像时发现,嫌疑人在案发前后在城市中不同地点出现过。他意识到,要判断嫌疑人是否有足够的时间作案,就需要计算嫌疑人在城市中移动的距离。
第一种距离计算方式就像是在城市的直线路径中穿梭。假如城市的道路都是笔直且相互垂直的,嫌疑人可以沿着直线从一个地点直接到达另一个地点,这种距离就像是连接两点的直线长度,这就是欧几里得距离。就好比在空旷的原野上,你可以直接朝着目标直线前进,这是最短的路径。
然而,这座城市的道路并非都是畅通无阻的直线。大部分道路都是呈网格状分布,嫌疑人只能沿着街道的直角转弯行走。就像在棋盘上移动棋子一样,只能横向或纵向移动,这种沿着网格线行走的距离就是曼哈顿距离。在城市中,车辆和行人大多遵循这样的规则移动。
还有一种情况,如果嫌疑人非常熟悉城市的地形,他知道一些捷径,比如通过一些小巷子或者秘密通道,他可以在某些情况下快速地从一个地点到达另一个地点,就好像他能瞬间跨越两点之间的最大横向或纵向差距,这种只考虑两点之间最大坐标差值的距离就是切比雪夫距离。(切比雪夫距离就好像,能同时在东西和南北两方向上运动,取两方向上最长运动时间记)
林探长通过这三种不同的距离计算方式,结合嫌疑人在各个地点出现的时间,最终找到了真正的罪犯。原来,罪犯利用了城市中特殊的地形和交通规则,巧妙地制造了不在场证明,但在数学的精确计算下,他的罪行还是暴露了。
二、图形解释
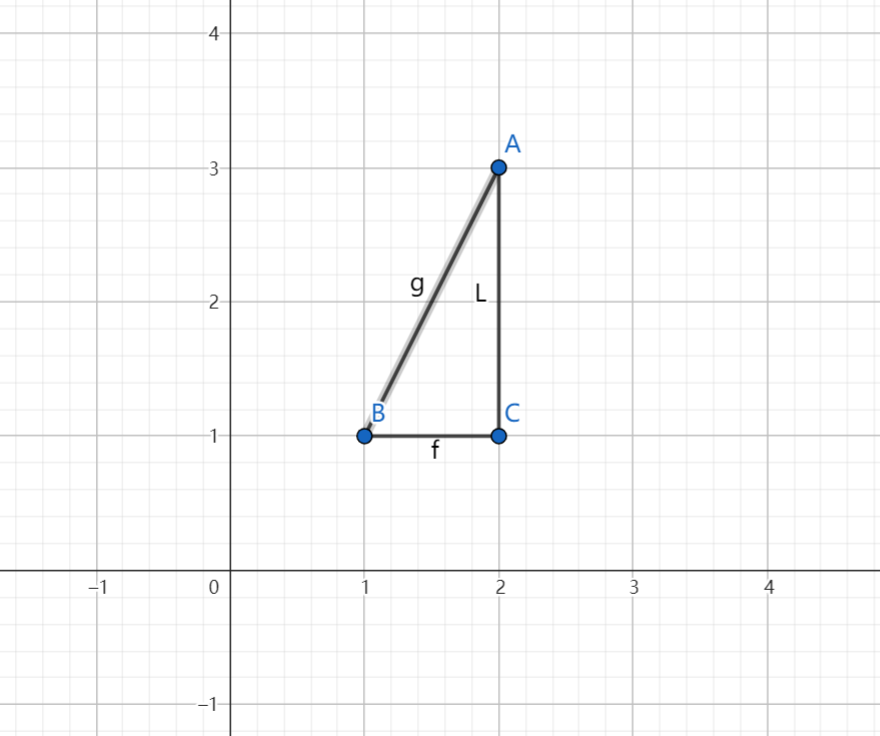
二维平面内点A与点B
之间的几种距离:
欧几里得距离=|g|=
曼哈顿距离=|f|+|L|=
切比雪夫距离=max(|f|,|L|)=
三、概念解释
欧几里得距离是两点间的直线距离。
二维空间:
三维空间:
n维空间:
曼哈顿距离(Manhattan Distance)是几何空间中测量两点之间距离的一种方式,它表示两个点在标准坐标系上的绝对轴距总和。具体来说,曼哈顿距离是两点在南北方向上的距离加上在东西方向上的距离,公式为:d(i,j)=|xi-xj|+|yi-yj|。
对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离因此曼哈顿距离又称为出租车距离,曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同。
切比雪夫距离(Chebyshev distance)是指在任意坐标维度上两个向量之间的最大差值。它也被称为棋盘距离,因为在国际象棋中,国王从一个方格移动到另一个方格的最小步数等于切比雪夫距离。其公式为:d(p, q) = max(|pᵢ - qᵢ|),其中p和q是两个点的坐标。切比雪夫距离广泛应用于图像处理、国际象棋等领域,但对异常值敏感。
在西洋棋里,车(城堡)是以曼哈顿距离来计算棋盘格上的距离;而王(国王)与后(皇后)使用切比雪夫距离,象(主教)则是用转了45度的曼哈顿距离来算(在同色的格子上),也就是说它以斜线为行走路径。只有国王需要一步一步走的方式移动,皇后、主教与城堡可以在一或两次移动走到任何一格(在没有阻碍物的情况下,且主教忽略它不能走到的另一类颜色)。
四、转换
切比雪夫距离与曼哈顿距离的相互转换
A(x1,y1)
B(x2,y2)
切比雪夫距离
曼哈顿距离
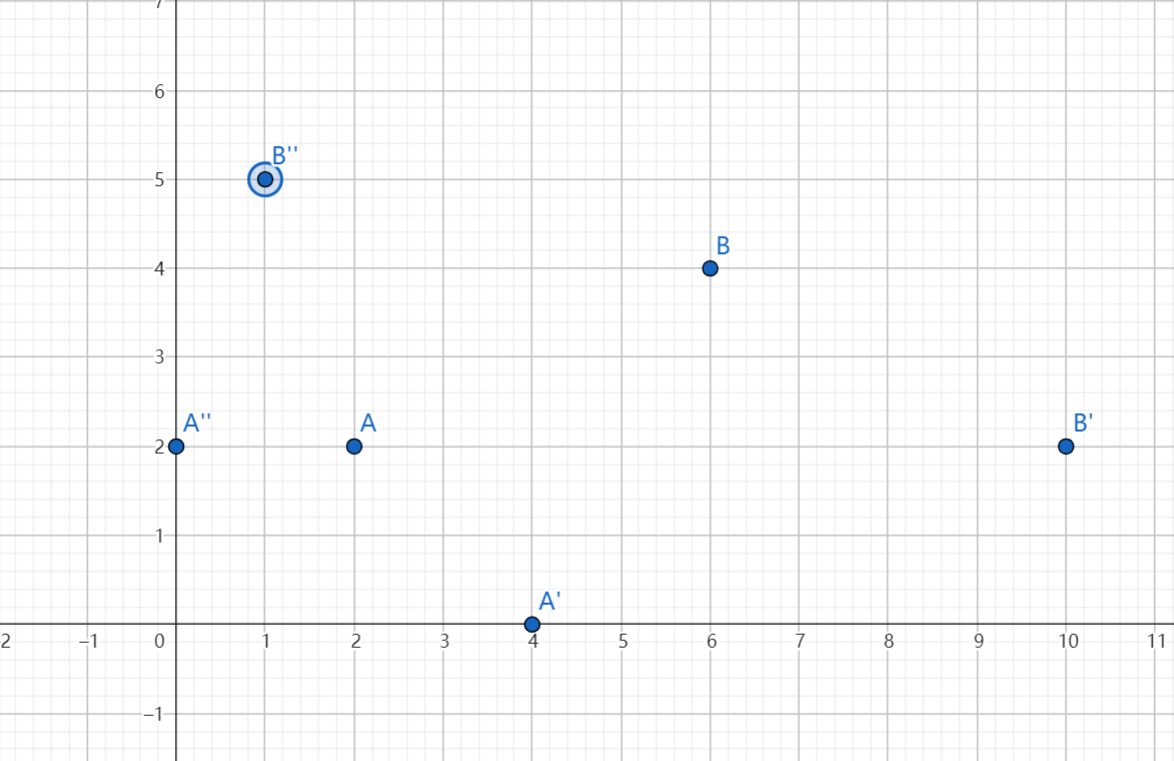
将点(x,y)映射到(x+y,x-y),原先两点间曼哈顿距离等于映射后两点间切比雪夫距离。
例:下图将点A映射到点A',将点B映射到点B'。
将点(x,y)映射到((x-y)/2,(x+y)/2),原先两点间切比雪夫距离等于映射后两点间曼哈顿距离。
例:下图将点A映射到点A'',将点B映射到点B''。