线性回归的应用
一·介绍
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
(用于线性回归任务,通过拟合数据找到最优线性模型,实现对连续目标值的预测 )
1. 参数
fit_intercept
(控制模型是否拟合截距项,若为False,回归直线过原点 )normalize
(决定是否对输入数据做归一化处理 )copy_X
(设置是否复制输入特征矩阵X,False时会直接覆盖原数据 )n_jobs
(指定并行计算的任务数,-1表示利用所有 CPU 加速,适用于多目标大规模场景 )
2. Attributes(属性,模型训练后可获取 )
coef_
(存储线性回归的特征系数,多目标任务返回二维数组,单目标返回一维数组 )intercept_
(线性模型的截距项,即独立于特征的偏移值 )
3. 方法
fit(X, y[, n_jobs])
(用训练集X和标签y训练模型,学习特征与标签的线性关系 )predict(X)
(用训练好的模型,对输入X(测试集或新数据)做预测 )score(X, y[, sample_weight])
(评估模型在数据集X和标签y上的预测效果,可带样本权重 )
二·代码部分
1·一元线性回归
csv数据
广告投入,销售额
29,77
28,62
34,93
31,84
25,59
29,64
32,80
31,75
24,58
33,91
25,51
31,73
26,65
30,84
#x y
2·代码
import pandas as pd#pandas基于numpy封装的 #列名 LinearRegression: <class 'sklearn.lin.^A1 ^16
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression"""
相关关系:包含因果关系和平行关系
因果关系:回归分析【原因引起结果,需要明确自变量和因变量】
平行关系:相关分析【无因果关系,不区分自变量和因变量】
"""data = pd.read_csv("data.csv")
a = data.广告投入
#绘制散点图
plt.scatter(data.广告投入, data.销售额)
plt.show()corr = data.corr()#求x和y的相关系数
#估计模型参数,建立回归模型
lr = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]lr.fit(x,y)#第四步、对回归模型进行检验
"""此处的score指R方"""
result = lr.predict(x)
score = lr.score(x, y)a = round(lr.intercept_[0],2)#查看截距
b = round(lr.coef_[0][0], 2)#查看斜率
print("线性回归模型为: y = {}x + {}.".format(b, a))#第五步、利用回归模型进行预测
predict = lr.predict([[40], [45], [50]])
print(predict)
data = pd.read_csv("data.csv")
a = data.广告投入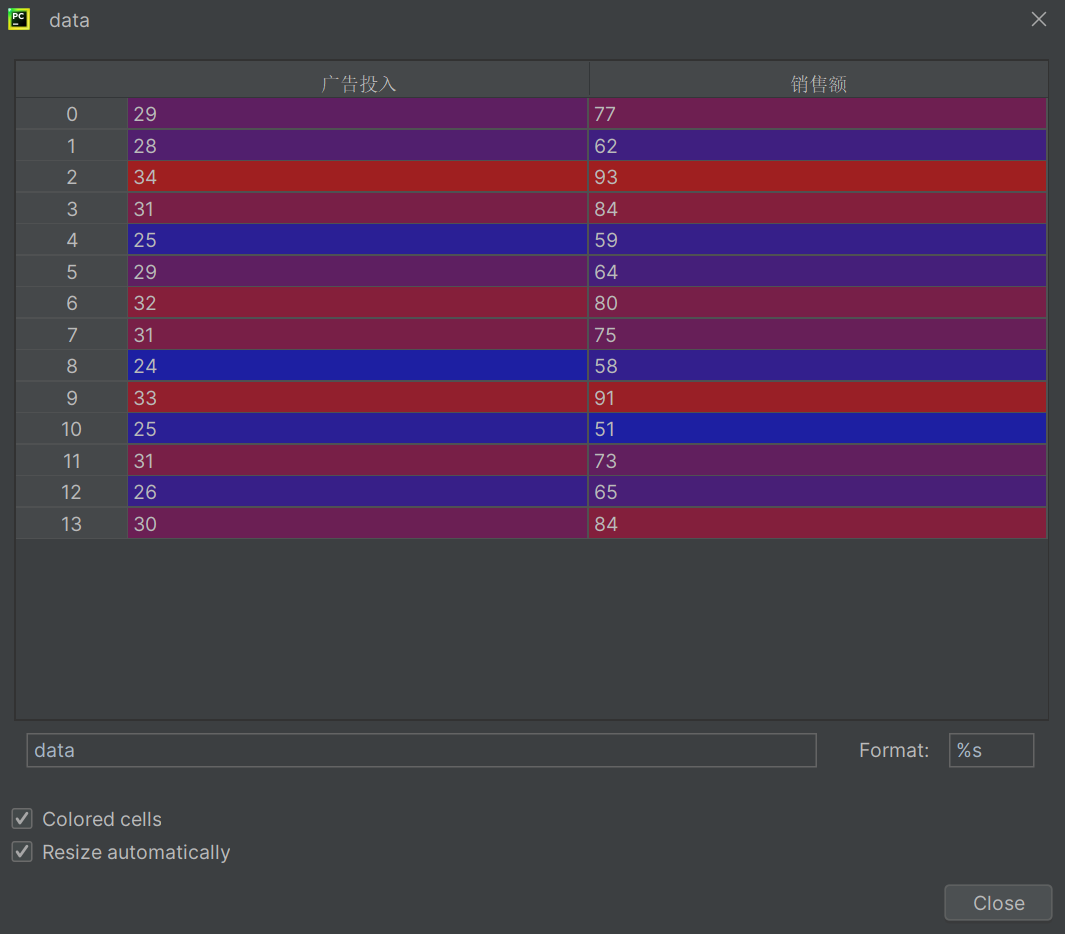
#绘制散点图
plt.scatter(data.广告投入, data.销售额)
plt.show() 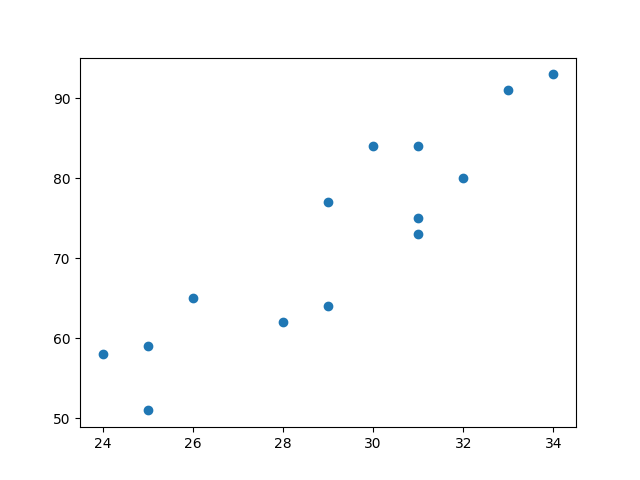
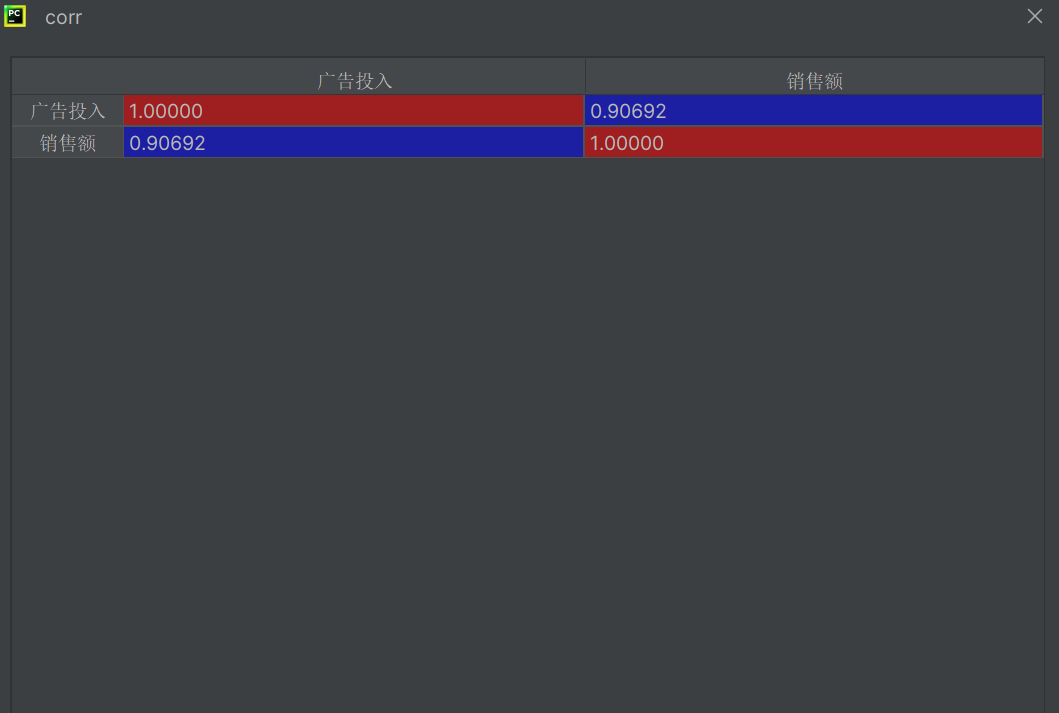
corr = data.corr()#求x和y的相关系数
#估计模型参数,建立回归模型
lr = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]相关系数
又称皮尔逊相关系数,是研究变量之间相关关系的度量,一般用字母 r 表示。
计算方式:
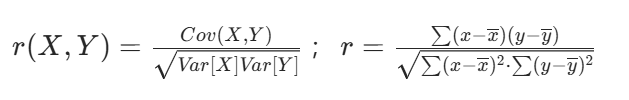
(Cov(X,Y))为X与Y的协方差
(Var[X])为X的方差
(Var[Y])为Y的方差
相关系数
相关系数解释:
1. |r| 0.8时,可视为两个变量之间高度相关
2. 0.5 |r| < 0.8时,可视为中度相关
3. 0.3 |r| < 0.5$时,视为低度相关
4. |r| < 0.3时,说明两个变量之间的相关程度极弱,可视为不相关
DataFrame数据列表
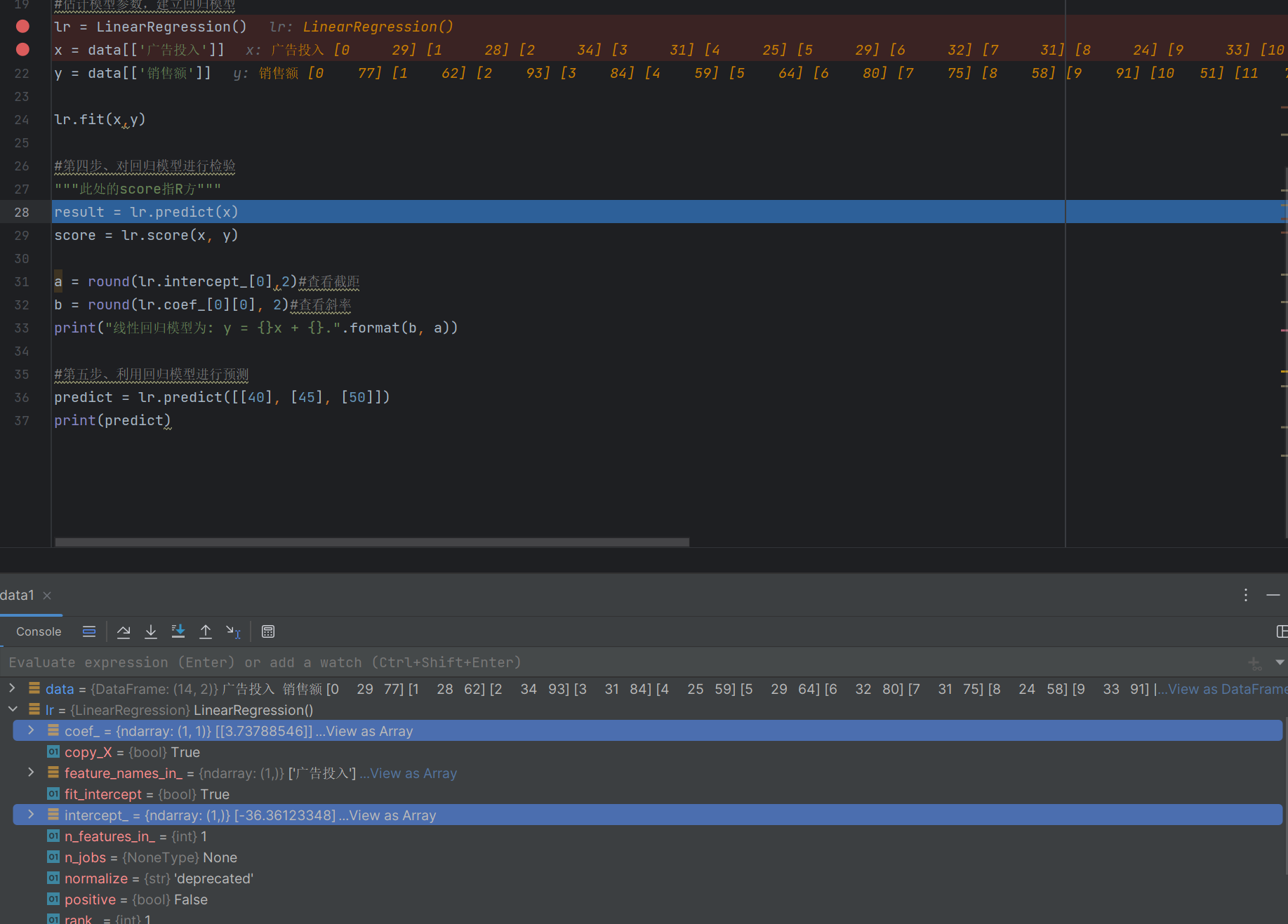
y=coef x+intercept y=3.7379x+-36.36123
测试的结果
#第四步、对回归模型进行检验
"""此处的score指R方"""
result = lr.predict(x)
score = lr.score(x, y) 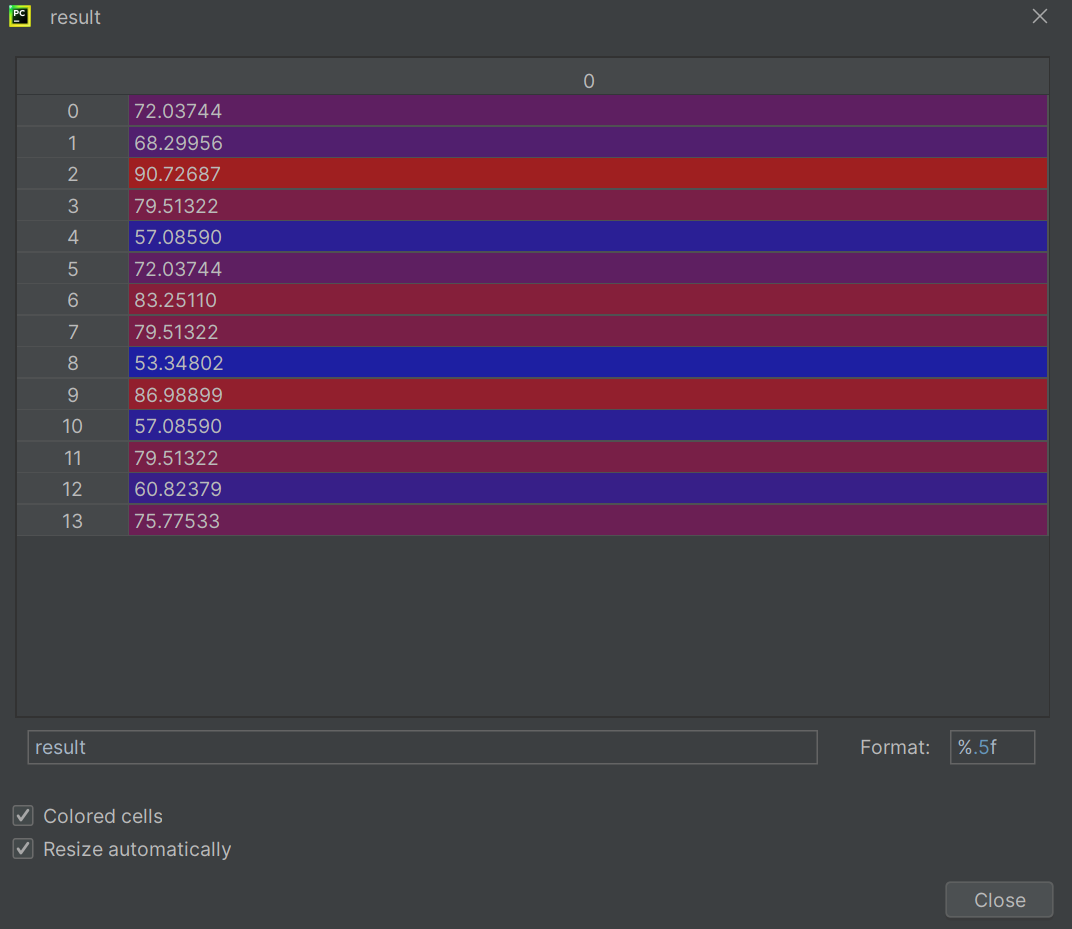
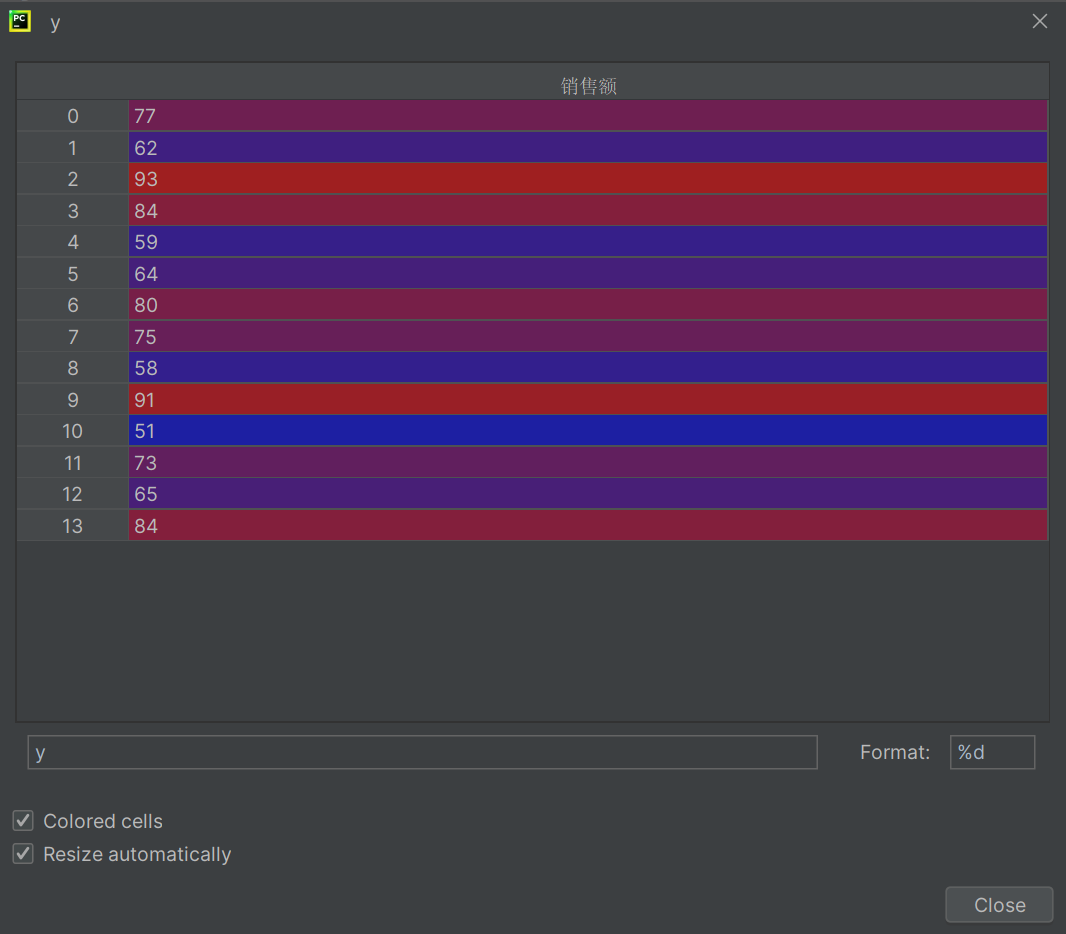
真实的结果就是y
对比观察
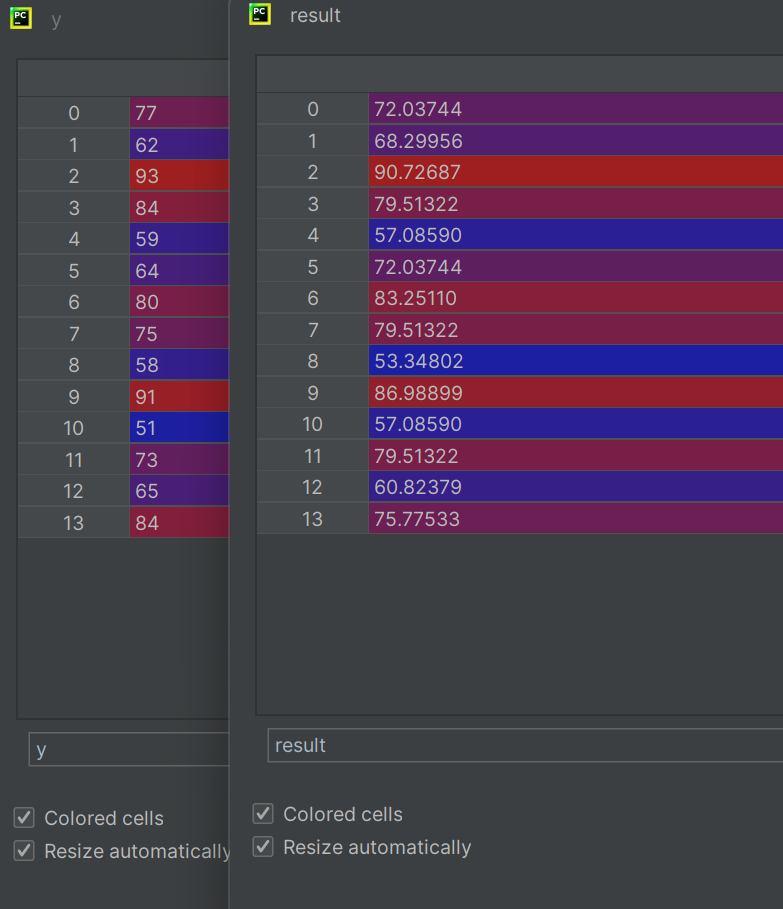
回归:得到 1 个具体的连续性的值
如何判断?
拟合优度
即判定系数 R 方,计算公式如下:
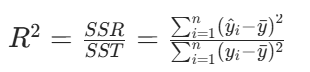
SSR: 回归平方和
SST: 离差平方和
1. 反映了回归直线的拟合程度。
2. 取值范围在 [0,1] 之间。
3.R 方越接近 1,说明拟合效果越好;R 方越接近 0,说明拟合效果越差。
4.R 方的平方根是相关系数。
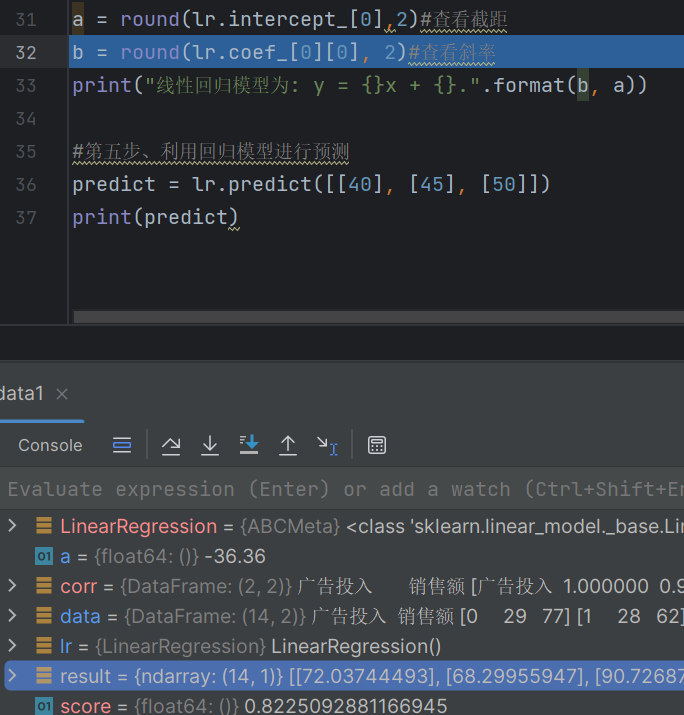
返回值说明
a = round(lr.intercept_[0],2)#查看截距
b = round(lr.coef_[0][0], 2)#查看斜率
print("线性回归模型为: y = {}x + {}.".format(b, a)) 
2·多线线性回归
import pandas as pd
from sklearn.linear_model import LinearRegression# 导入数据
data = pd.read_csv("多元线性回归.csv", encoding='gbk', engine='python')# 打印相关系数矩阵
corr = data[["体重", "年龄", "血压收缩"]].corr()# 第二步,估计模型参数,建立回归模型
lr_model = LinearRegression()
x = data[['体重', '年龄']]
y = data[['血压收缩']]lr_model.fit(x, y) # 训练模型# 第四步,对回归模型进行检验
score = lr_model.score(x, y) # sklearn statsmodes(数理统计这个专业)# 第五步,利用回归模型进行预测
print(lr_model.predict([[80, 60]]))
print(lr_model.predict([[70, 30], [70, 20]]))# 获取自变量系数和截距
a = lr_model.coef_
b = lr_model.intercept_
print("线性回归模型为: y = {:.2f}x1 + {:.2f}x2 + {:.2f}.".format(a[0][0], a[0][1], b[0]))