数据结构——图(二、图的存储和基本操作)
一、邻接矩阵
1、邻接矩阵定义
一个一维数组存储图中顶点的信息,一个二维数组存储图中边的信息(各顶点之间的邻接关系)。
邻接矩阵可用来存储无向图、有向图
若图中有n个顶点,则邻接矩阵A是n
n
邻接矩阵采用顺序存储结构
空间复杂度为O(|V|²)
与边数无关
存储顶点信息使用O(|V|),存储边信息使用O(|V|²)
更多用于稠密图
1)无向图的邻接矩阵
注:对称矩阵且唯一,对称矩阵在实际存储时只需要存储上(下)三角矩阵中的元素
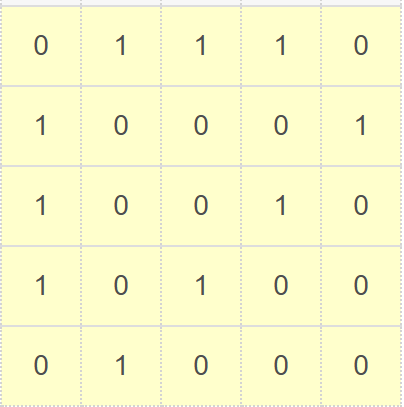
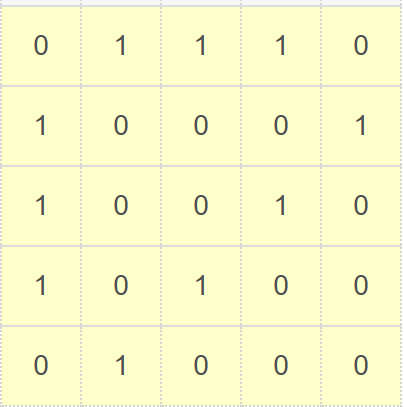
| 如右表黄色区域,有向图的邻接矩阵。 G[i][j]=0,两顶点间不存在边 G[i][j]=1,两顶点间存在边 | 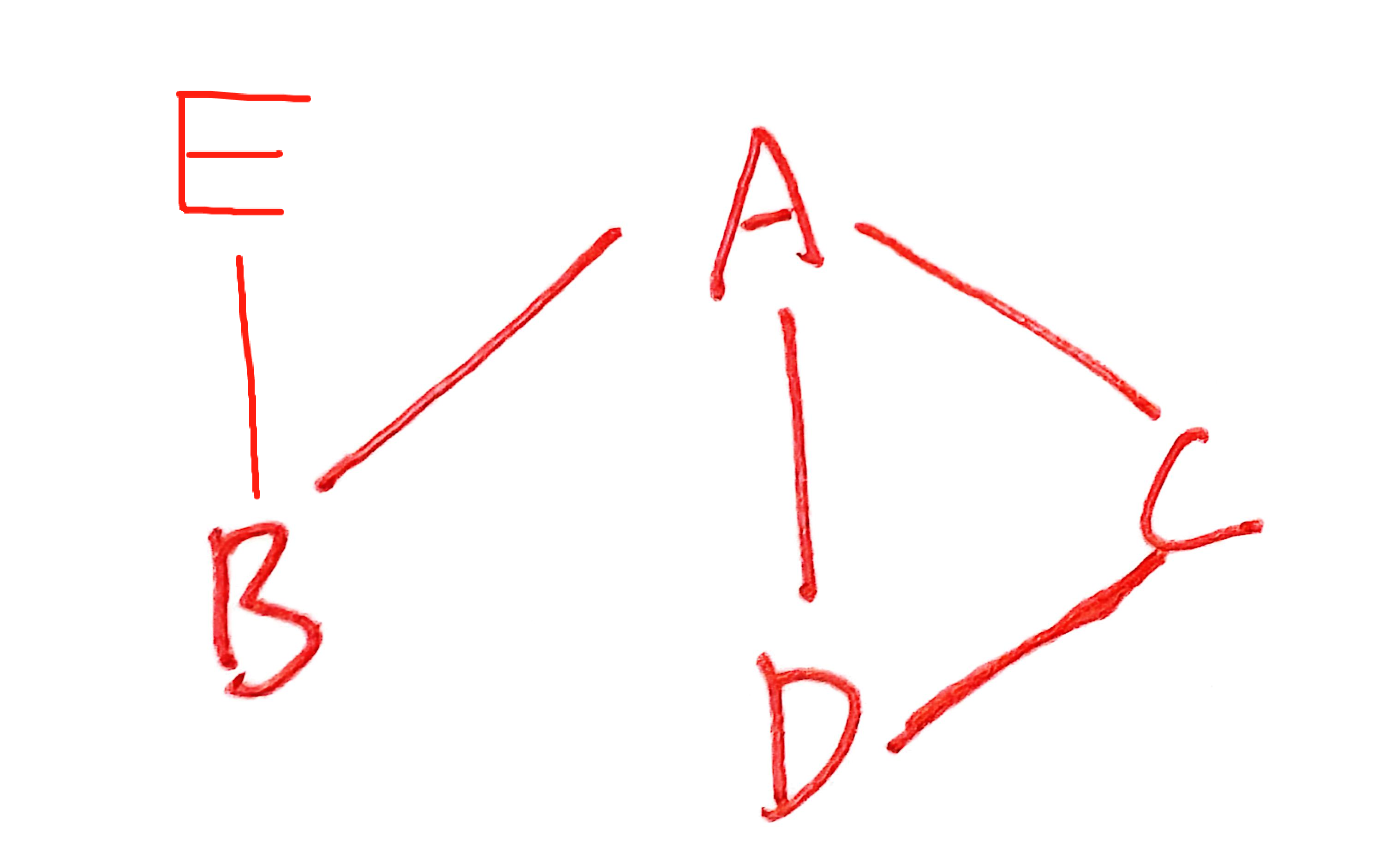 | 0 | 1 | 2 | 3 | 4 | |
| A | B | C | D | E | |||
| 0 | A | 0 | 1 | 1 | 1 | 0 | |
| 1 | B | 1 | 0 | 0 | 0 | 1 | |
| 2 | C | 1 | 0 | 0 | 1 | 0 | |
| 3 | D | 1 | 0 | 1 | 0 | 0 | |
| 4 | E | 0 | 1 | 0 | 0 | 0 | |
对于无向矩阵
度遍历行或列
顶点A的度 = 邻接矩阵第0行(或第0列)的非零元素(或非∞元素)的个数之和
时间复杂度为O(|V|)
2)有向图的邻接矩阵
注:唯一,但是由于两个点之间的边是双向的,因此并不对称
| 如右表黄色区域,有向图的邻接矩阵。 G[i][j]=0,顶点i到顶点j不存在弧 G[i][j]=1,顶点i到顶点j存在弧 | 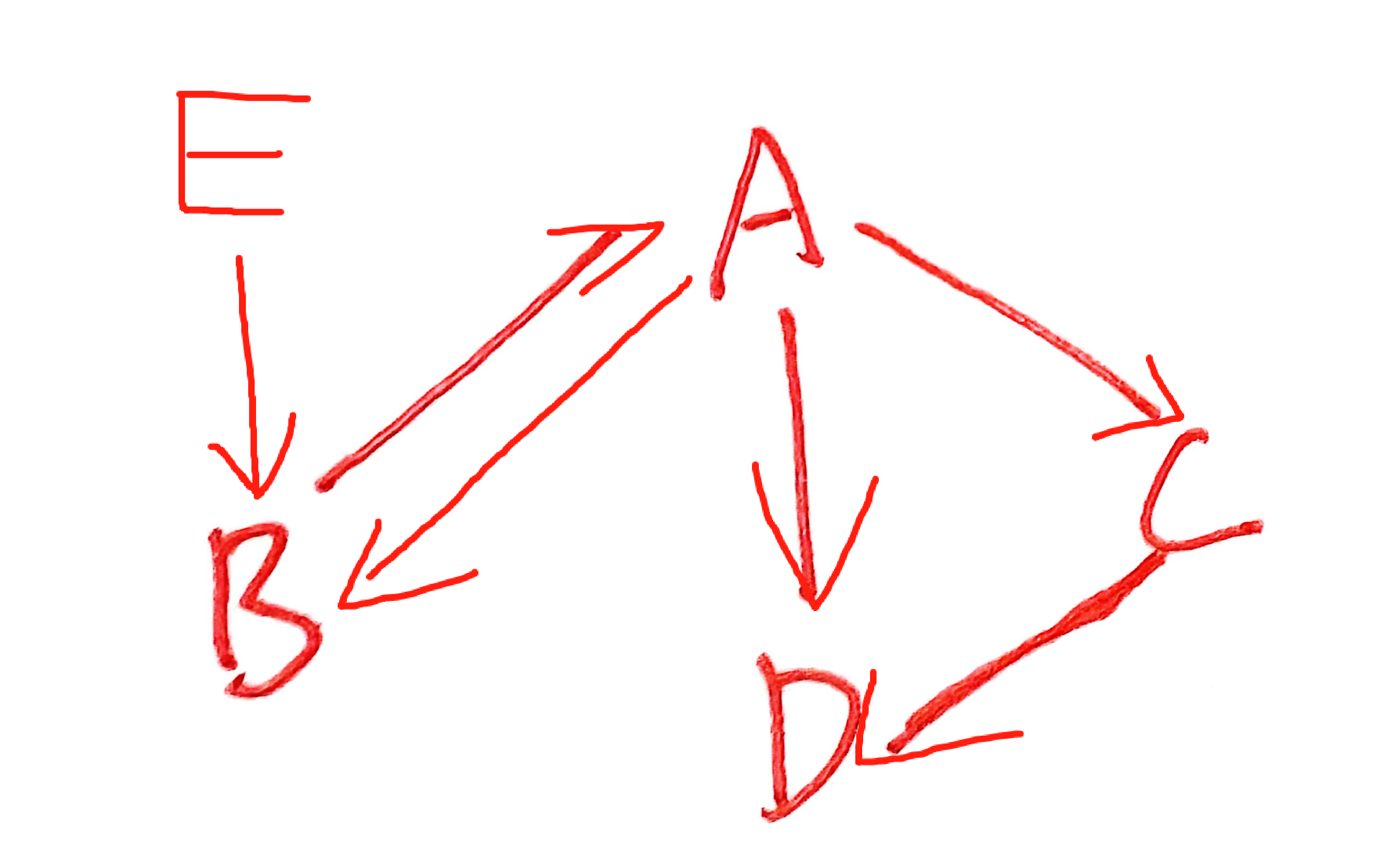 | 0 | 1 | 2 | 3 | 4 | |
| A | B | C | D | E | |||
| 0 | A | 0 | 1 | 1 | 1 | 0 | |
| 1 | B | 1 | 0 | 0 | 0 | 0 | |
| 2 | C | 0 | 0 | 0 | 1 | 0 | |
| 3 | D | 0 | 0 | 0 | 0 | 0 | |
| 4 | E | 0 | 1 | 0 | 0 | 0 | |
对于有向矩阵
出度遍历行,入度遍历列
顶点A的度 = 出度+入度 = 邻接矩阵第0行的非零元素(或非∞元素)的个数 + 邻接矩阵第0列的非零元素 (或非∞元素)的个数 = 3+1 = 4
时间复杂度为O(|V|)+O(|V|)
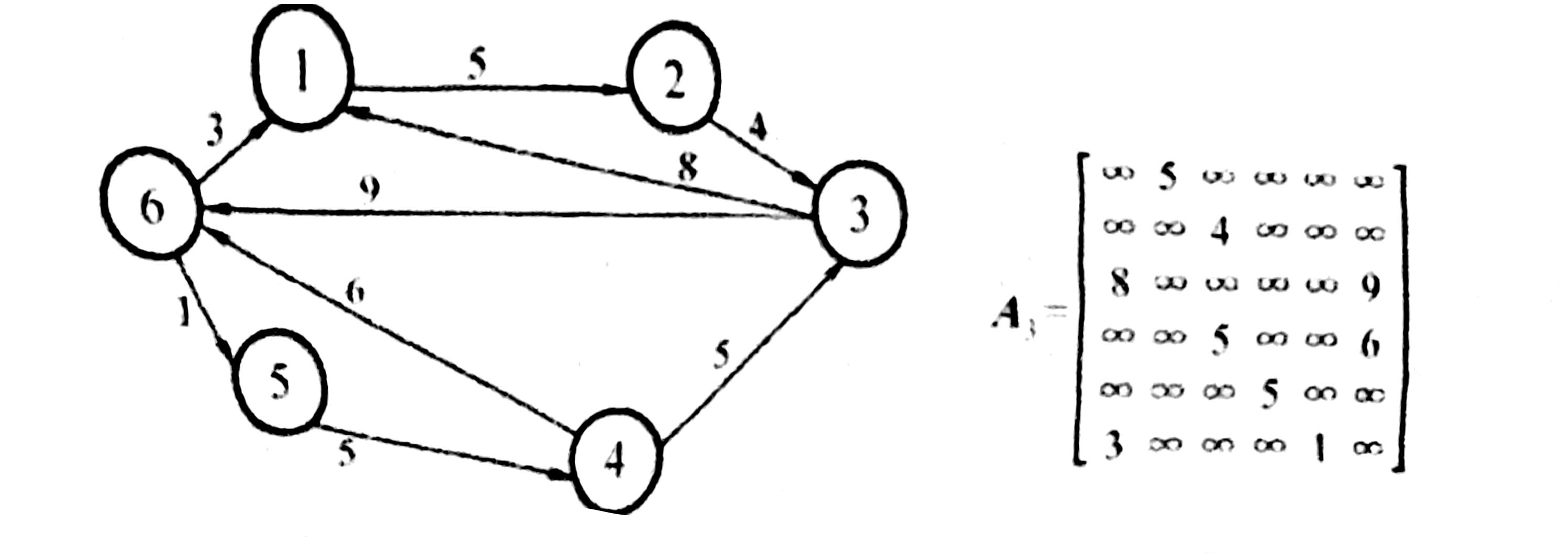
3)带权图的邻接矩阵
无穷∞表示两个顶点之间不存在边(也可以使用0表示)
2、邻接矩阵性质
用邻接矩阵存储图
1、很容易确定图中任意两个顶点之间是否有边相连
比如无向图中,判断A与D之间是否相连,检查G[0][3]==1或G[3][0]==1
2、若要确定图中有多少条边,必须按行、按列对每个元素进行遍历,时间复杂度为O(|V|²)
3、若要确定顶点的度,必须按行、按列对每个元素进行遍历,时间复杂度为O(|V|)
3、邻接矩阵存储结构(算法实现)
#define INFININITY //最大int值,即无穷
#define MAXVertexNum 100 //最大顶点数typedef char VerTexType; //顶点对应的数据类型
typedef int ArcType; //边对应的数据类型 typedef struct{VerTexType vexs[MAXVertexNum]; //顶点表ArcType arcs[MAXVertexNum][MAXVertexNum]; //邻接矩阵,边表int vexnum,arcnum; //图的当前点数和边数
}MGraph;1、在简单应用中,可以直接使用二维数组作为图的邻接矩阵(顶点信息可忽略)
2、当邻接矩阵的元素仅表示相应边是否存在时,EdgeType可用值为0或1的布尔类型
邻接矩阵具体算法操作查看
图——邻接矩阵基本操作算法实现-CSDN博客
4、邻接矩阵的相关计算
[1][1] = 顶点B到顶点B的长度为2的路径的数目
=第2行*第2列
=
=2
[0][3] = 顶点A到顶点D的长度为2的路径的数目
=第1行*第4列
=
=1

二、邻接表
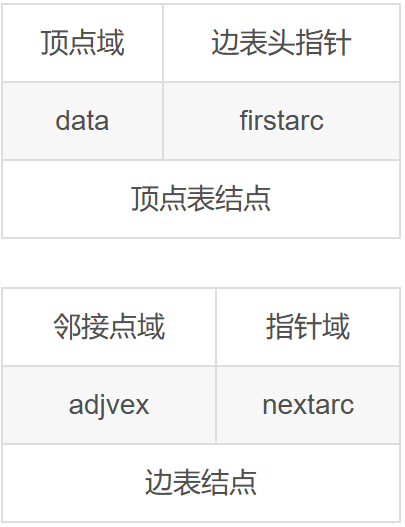
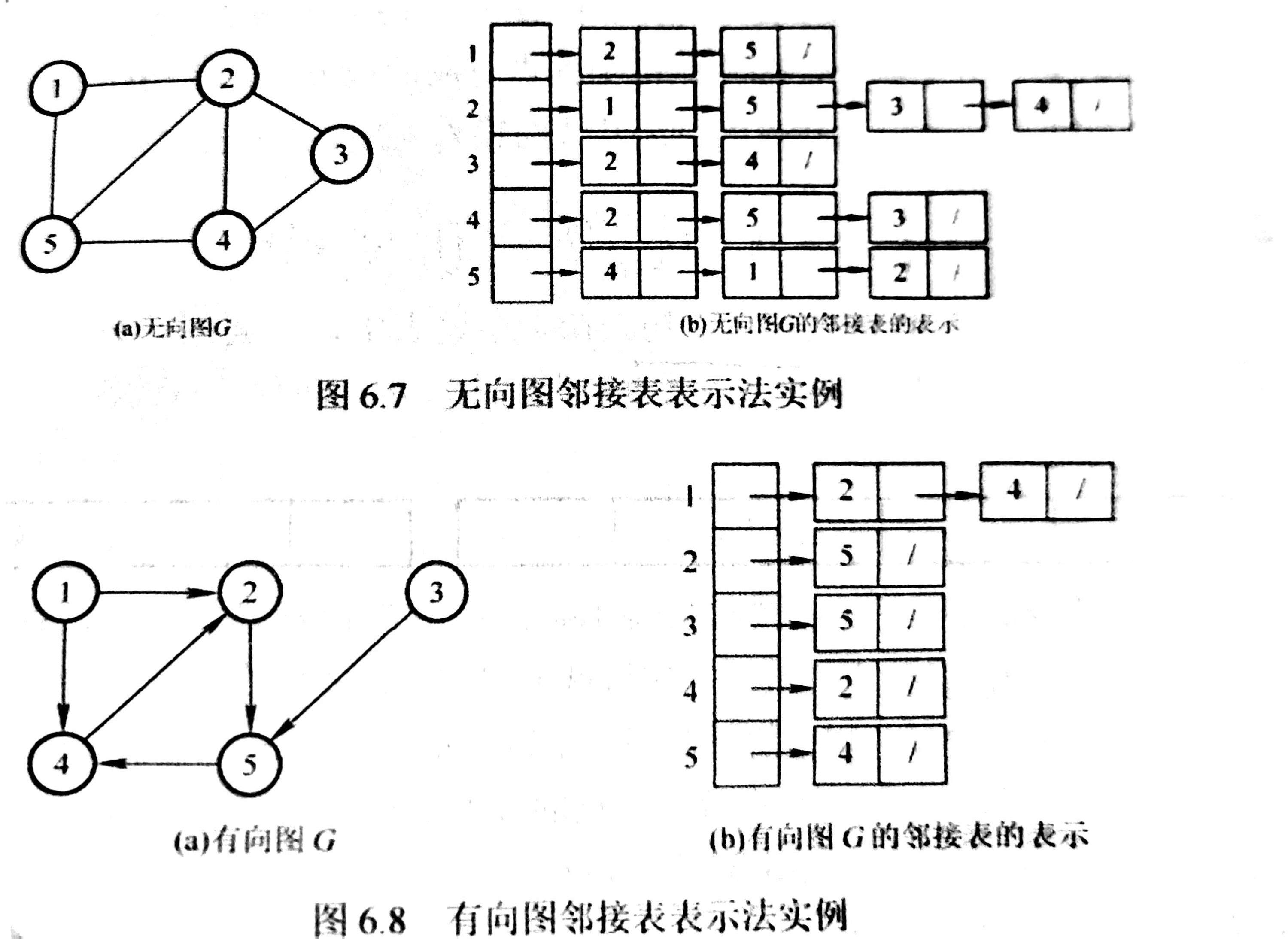
1、邻接表定义
对图中每个顶点建立一个单链表,第i个单链表中的结点表示依附于顶点i的边(对于有向图则是以顶点i为尾的弧),称为边表(对于有向图则是出边表)
边表的头指针和顶点的数据信息采用顺序存储,即顶点表
结合顺序存储和链式存储
若G为无向图,则所需存储空间为O(|V|)+O(2|E|),因为每条边在邻接表出现两次
若G为有向图,则所需存储空间为O(|V|)+O(|E|)
2、邻接表的存储结构(算法实现)
#define MAXVertexNum 100 //最大顶点数typedef struct ArcNode{ //边表结点 int adjvex; //该边所指向的顶点的位置 struct ArcNode *nextarc;//指向下一条边的指针 Otherinfo info; //网的边权值
}ArcNode;typedef struct VNode{ //顶点结点VerTexType data; //顶点信息ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VNode,AdjList[MAXVertexNum];//AdjList表示邻接表类型typedef struct{ AdjList vertices; //邻接表int vexnum,arcnum; //图的当前顶点数和弧数
}ALGraph;
关于邻接表更多具体基础操作算法查看附件
图——邻接表基本操作算法实现-CSDN博客
3、邻接表性质
1、对于稀疏表(边数较少的表),采用邻接表将极大节省空间
2、图的邻接表不唯一,在每个顶点对应的边表中,各边结点的链接次序可以是任意的,取决于建立邻接表的算法及边的输入次序。
1、给定一个顶点,极其容易找出它的所有邻边(对于有向图,则是出边)
遍历该顶点的单链表,最差时间复杂度为O(|V|)
2、对于有向图,找一个顶点A的入边,需要遍历所有顶点(除该顶点A外)的边表,找到结点A,时间复杂度为O(|E|)
3、若要确定两个顶点间是否存在边,找到相应结点对应的边表中查找另一个结点
对于有向图,如果出边未找到,还需要遍历所有顶点(除自身)的边表,找到自身结点。
4、在有向图的邻接表中,求某个顶点的出度只需要计算其邻接表中的边表个数,但求某个顶点x的入度则需要遍历全部邻接表,统计邻接点域为x的边表结点个数。
三、十字链表
是有向图的一种链式存储结构
有向图的每条弧用一个结点(弧节点)表示,每个顶点用一个(顶点结点)表示
解决入边难寻的问题,同时节省存储空间,空间复杂度为O(|V|+|E|)
| data | firstin | firstout |
| 数据信息 | 指向以该顶点为弧头的第一条弧 | 指向以该顶点为弧尾的第一条弧 |
| tailex | headvex | hlink | tlink | (info) |
| 弧尾编号 | 弧头编号 | 指向弧头相同的下一条弧 | 指向弧尾相同的下一条弧 | 弧的相关信息 |
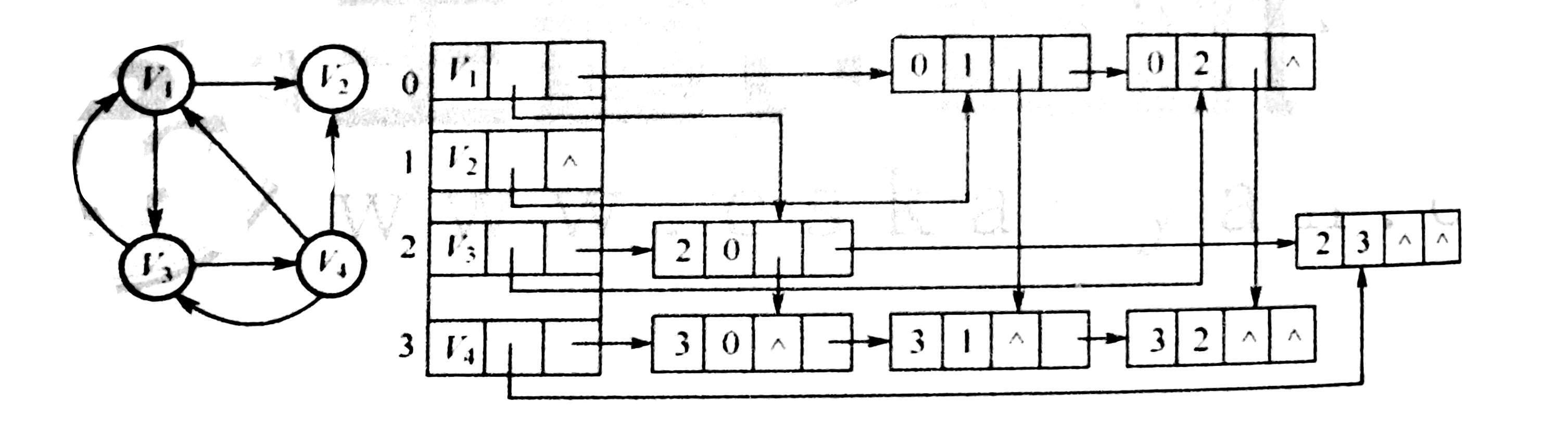
顶点结点之间是顺序存储,弧结点省略了info域
图的十字链表不是唯一的,但是一个十字链表表示唯一确定的一个图
在十字链表中,既容易找到以V为尾的弧,也容易找到以V为头的弧,因而容易求得顶点的出度和入度
四、邻接多重表
邻接多重表是无向图的一种链式存储
解决邻接表中求两个顶点之间是否存在边而执行删除边等操作时,需要分别遍历两个顶点的边表的问题。
| ivex | ilink | jvex | tlink | (info) |
| 顶点编号 | 依附于顶点ivex的下一条边 | 另一个顶点编号 | 依附于顶点jvex的下一条边 | 弧的相关信息 |
| data | firstedge |
| 数据信息 | 依附于该顶点的第一条边 |
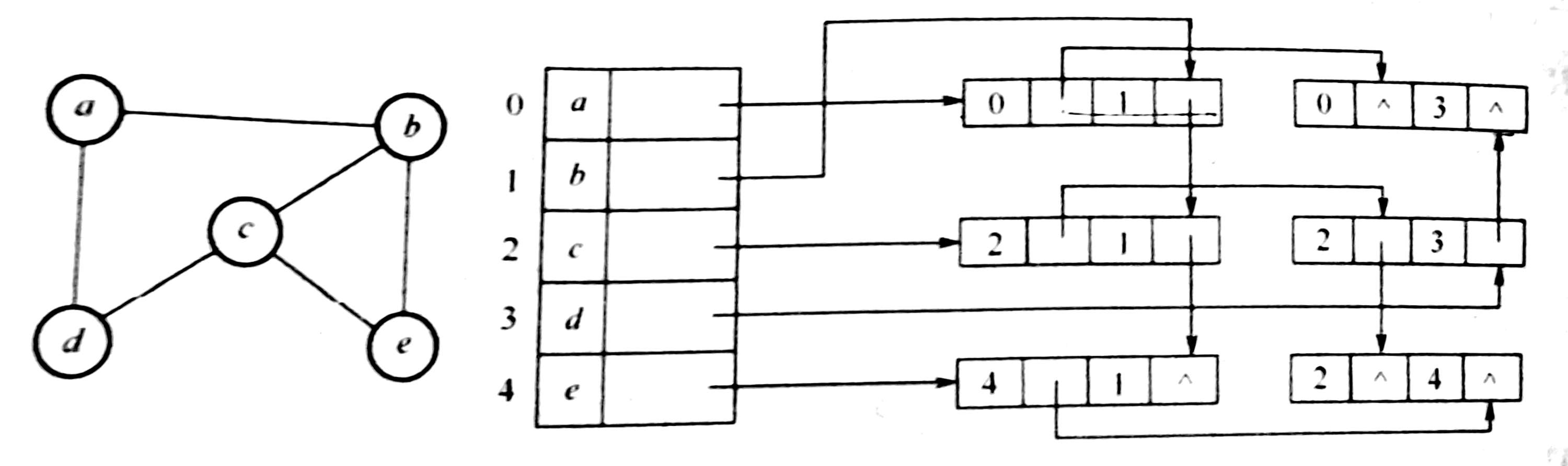
在邻接多重表中,所有依附于同一顶点的边串联在同一链表中
因为每条边依附于两个顶点,所以每个边结点同时链接在两个链表中
邻接多重表和邻接表的区别
同一条便在邻接表中用两个结点表示,在邻接多重表中只有一个结点
五、图的基本操作
Adjacent(G,x,y) 判断图是否存在边<x,y>或(x,y)
Neighbors(G,x) 列出图中与结点x邻接的边
InsertVertex(G,x) 在图中插入顶点x
DeleteVertex(G,x) 在图中删除顶点x
AddEdge(G,x,y) 若无向边(x,y)或有向边<x,y>不存在,则向图G中添加该边
RemoveEdge(G,x,y) 若无向边(x,y)或有向边<x,y>存在,则从图G中删除该边
FirstNeighbor(G,x) 求图中顶点x的第一个邻接点,若有则返回定点好,若x没有邻接点或图中不存在x,则返回-1
NextNeighbor(G,x) 假设图中顶点y是顶点x的一个邻接点,返回除y外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1
Get_edge_value(G,x,y) 获取图中边(x,y) 或 <x,y>对应的权值
Set_edge_value(G,x,y,v) 设置图中边(x,y) 或 <x,y>对应的权值为v
| V表示顶点数、E表示边数,此表显示最差所需消耗时间,时间复杂度取最高量级即可 这里假设顶点为A、B、C,因此,需要知道索引需要遍历顶点集操作,时间复杂度为O(|V|),下表中均省略这一步的时间复杂度 | ||||
| 操作 | 邻接矩阵 | 邻接表 | ||
| 有向图 | 无向图 | 有向图 | 无向图 | |
| InsertVertex(G,x) 插入顶点 | O(1) | O(1) | O(1) | O(1) |
| DeleteVertex(G,x) 删除顶点 | O(|V|²) | O(|V|²) | O(|V| + |E|) | O(|V| + 2|E|) |
| 找到顶点索引,删除顶点所在行列 | 找到顶点索引,删除顶点链接的所有边表结点 遍历所有边表结点,删除该顶点的边表结点 | |||
| AddEdge(G,x,y) 插入边 | O(1) | O(1) | O(1) | O(2) |
| 找到两个顶点的索引,设置 G.arcs[i][j](G.arcs[i][j]与G.arcs[j][i]) | 找到两个顶点的索引, 在顶点表找到弧头, 在该顶点表结点的边表头指针后添加边表结点 | 找到两个顶点的索引, 分别在这两个顶点表结点的边表头指针后添加边表结点 | ||
| RemoveEdge(G,x,y) 删除边 | O(1) | O(1) | O(|V|) | O(2|V|) |
| 找到两个顶点的索引,设置 G.arcs[i][j](G.arcs[i][j]与G.arcs[j][i]) | 找到边的弧头索引, 遍历该弧头的边表结点 | 找到两个顶点的索引, 分别遍历两个顶点的边表结点 | ||
| Adjacent(G,x,y) 判断图是否存在边<x,y>或(x,y) | O(1) | O(1) | O(|V|) | O(|V|) |
| 找到两个顶点的索引,判断 G.arcs[i][j](或G.arcs[j][i]) | 在顶点表找到弧头, 遍历该弧头的边表结点 | 找到某个顶点的索引, 遍历顶点的边表结点 | ||
| Neighbors(G,x) 列出图中结点x的邻接的边 | O(|V|) | O(|V|) | O(|V| + |E|) | O(|V|) |
| 找到结点x的索引,遍历结点x所在的行(或行列) | 在顶点表找到弧头,遍历该弧头的边表结点(出边) 遍历整个边表节点找弧头(入边) | 找到某个顶点的索引, 遍历顶点的边表结点 | ||
| FirstNeighbor(G,x) 获取第一个邻接点 | O(|V|) | O(|V|) | O(|E|) | O(1) |
| 找到结点x的索引,遍历结点x所在的行(或行列) | 找到结点x的索引, 遍历结点x的第一个边表结点 如果为空,遍历所有边表结点 | 找到结点x的索引, 遍历结点x的第一个边表结点 如果为空,则不存在 | ||
| NextNeighbor(G,x,y) 获取下一个邻接点 | O(|V|) | O(|V|) | O(|V|)+O(|E|) | O(|V|) |
| 找到结点x的索引,遍历结点x所在的行(或行列) | 在顶点表找到结点x,遍历结点x的边表结点,找到y的下一个结点 如果结点x的边表结点不存在,则在顶点表结点找到结点y,遍历顶点表结点y之后的所有顶点表结点的边表结点,如果找到结点x,则返回对应顶点结点 | 在顶点表找到结点x,遍历结点x的边表结点,找到y的下一个结点 | ||
| Get_edge_value(G,x,y) 获取边权值 | O(1) | O(1) | O(|V|) | O(|V|) |
| Set_edge_value(G,x,y,v) 设置边权值 | O(1) | O(1) | O(|V|) | O(2|V|) |
图的遍历算法见附件
数据结构——图(三、图的 广度/深度 优先搜索)-CSDN博客
六、图的四种存储方式总结对比
| 项目 | 邻接矩阵 | 邻接表 | 十字链表 | 邻接多重表 |
|---|---|---|---|---|
| 空间复杂度 | O(|V|²) | 无向图:O(|V| + 2|E|) 有向图:O(|V| + |E|) | O(|V| + |E|) | O(|V| + |E|) |
| 找相邻边 | 遍历对应行或列的时间 复杂度为O(|V|) | 找有向图的入度必须遍历整个邻接表 | 很方便 | 很方便 |
| 删除边或顶点 | 删除边很方便,删除顶点需大量移动数据 | 无向图中删除边或顶点都不方便 | 很方便 | 很方便 |
| 适用于 | 稠密图 | 稀疏图和其他 | 只能存有向图 | 只能存无向图 |
| 表示方式 | 唯一 | 不唯一 | 不唯一 | 不唯一 |