当前位置：首页 > news >正文

从零开始大模型之编码注意力机制

news 2025/7/27 10:07:57

从零开始大模型之编码注意力机制

1 长序列建模中的问题
2 使用注意力机制捕捉数据依赖关系
3 自注意力机制
4 实现带可训练权重的自注意力机制
5 利用因果注意力隐藏未来词汇
6 将单头注意力扩展到多头注意力
7 Pytorch附录
7.1 torch.nn.Linear

多头+掩码+可训练权重的注意力机制。
为什么要自注意力机制？为什么要带训练权重的自注意力机制？为什么要增加掩码功能？为什么要增加多头功能？

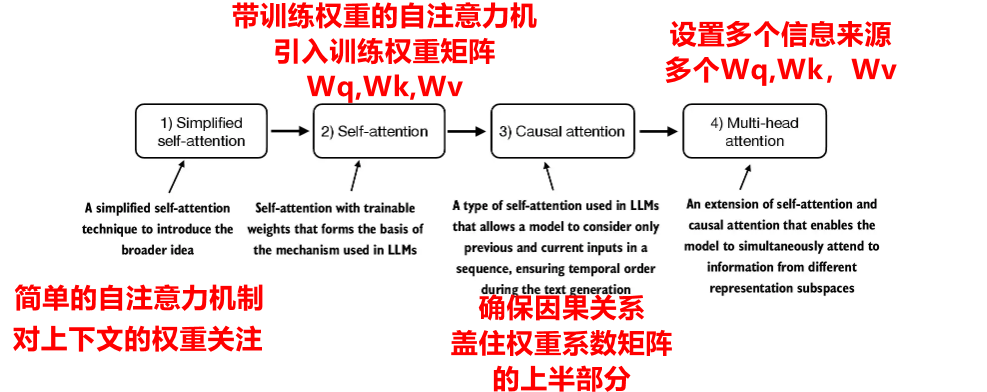
在这里插入图片描述

1 长序列建模中的问题

无注意力机制存在语法不对齐，以及没有联系上下文的缺点。Transformer相比传统的RNN能够解决较长距离的依赖。

2 使用注意力机制捕捉数据依赖关系

自注意力机制是transformer机制中一种重要机制，它通过允许一个序列种的每个位置与同一序列中其他所有位置进行交互并权衡其重要性，能够更高效的输入表示。

3 自注意力机制

自注意力机制是序列token中，当前token与前后上下文的token之间的线性组合关系构成，构成的这个向量叫做上下文向量。上下文向量 = 各个词元嵌入向量的加权和。
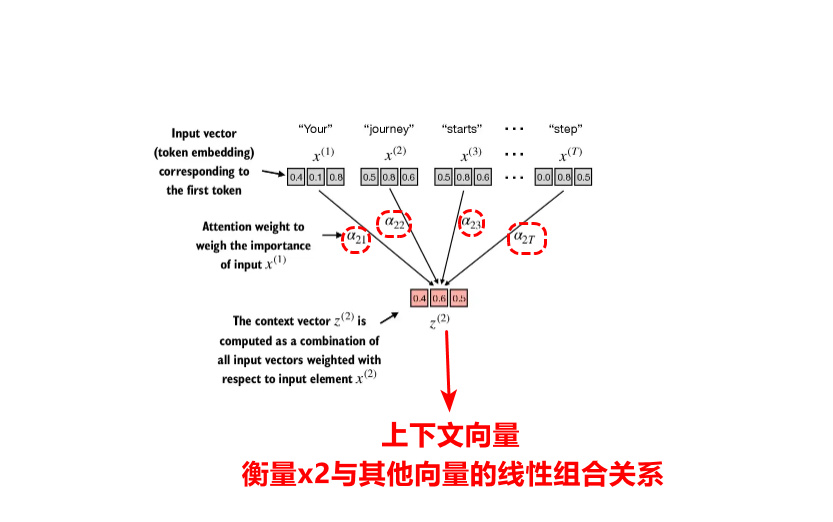
在这里插入图片描述
之所以引入注意力机制，就是为了进行语义的连贯，对于每个输入的token词元来说，不是独立的单独词元；这就像我们做阅读理解，总是要结合上下文要推敲某句话的含义是一样的，通过自注意力机制，让我们能够关注到当前文章内容与上下文之间的联系。
自注意力机制详细的操作步骤如下：
1.计算选定token的词元嵌入向量与所有token序列的词元嵌入向量点积就得到注意力分数
2.softmax归一化注意力分数
3.用归一化的注意力分数对词元嵌入向量加权求和，得到该位置的上下文向量，依次类推计算所有位置的上下文向量。
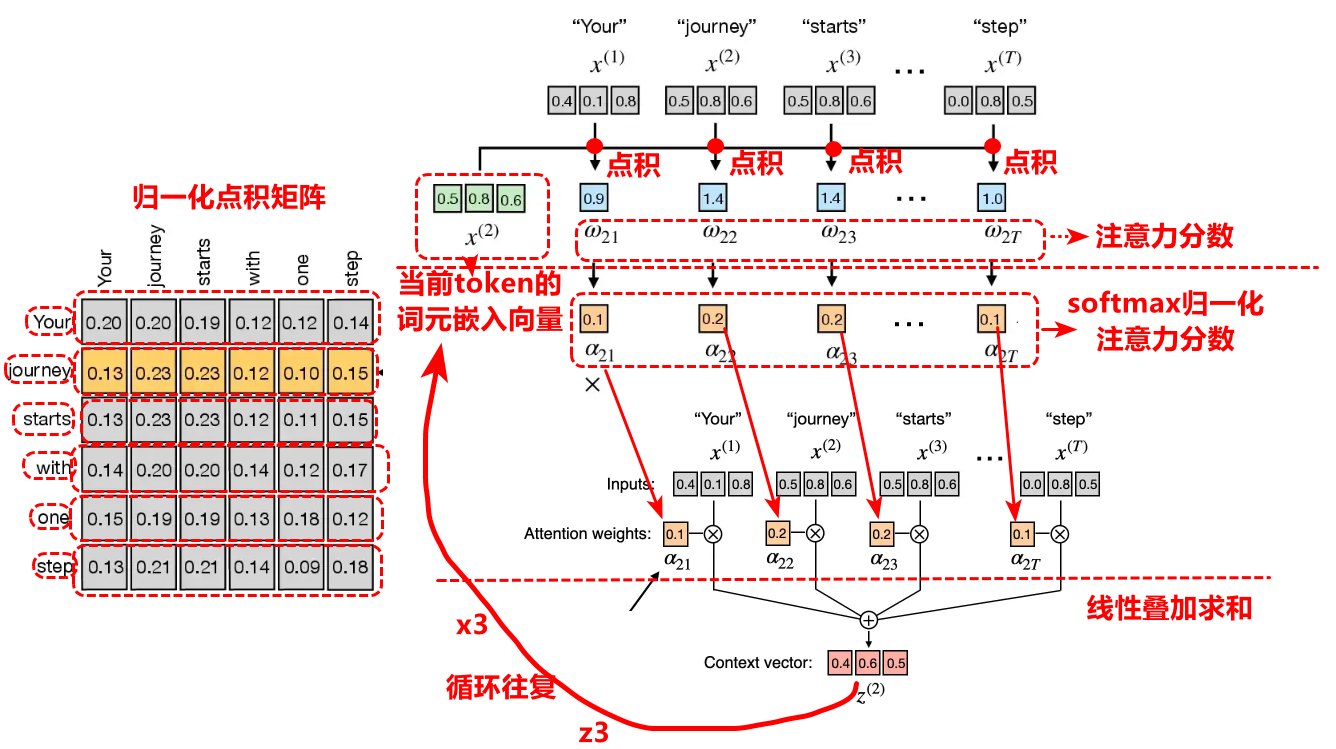
在这里插入图片描述

4 实现带可训练权重的自注意力机制

带可训练权重的自注意力机制是在简单的自注意力机制上引入了可训练权重矩阵Wq,Wk,Wv，通过反向传播算法进行更新，同时带可训练权重的自注意力机制又被称为是缩放点积注意力。引入带可训练权重的自注意力机制一方面是为了能够动态的联系上下文，这是因为简单的自注意力机制只能通过点积静态计算相关权重，另一方面受到人类在数据库中检索信息的启发，其本质是模仿人类搜索查询，其中Q代表query(查询)，K代表key(键)，V代表value(值)。
实现带可训练权重的自注意力机制仍然是三个核心步骤，计算权重系数，系数归一化，系数线性叠加。
第一步，对于每个词元嵌入向量，将q（query）查询向量依次定为第一个token,第二个token的嵌入向量，在确定某token下的查询向量，然后计算别的token的嵌入向量与权重矩阵Wk和Wv矩阵的乘积，可以得到k(key)键向量，v(value)值向量。
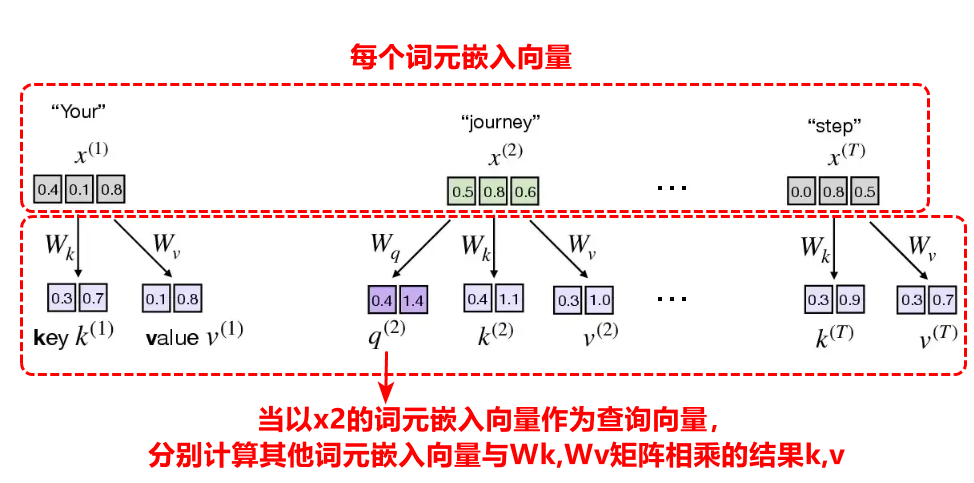
在这里插入图片描述
第二步将得到的当前的查询向量q2，与其他所有token的k向量进行点积就得到每个token在上下文向量的占比分数，将该分数进行softmax归一化后即为权重系数。

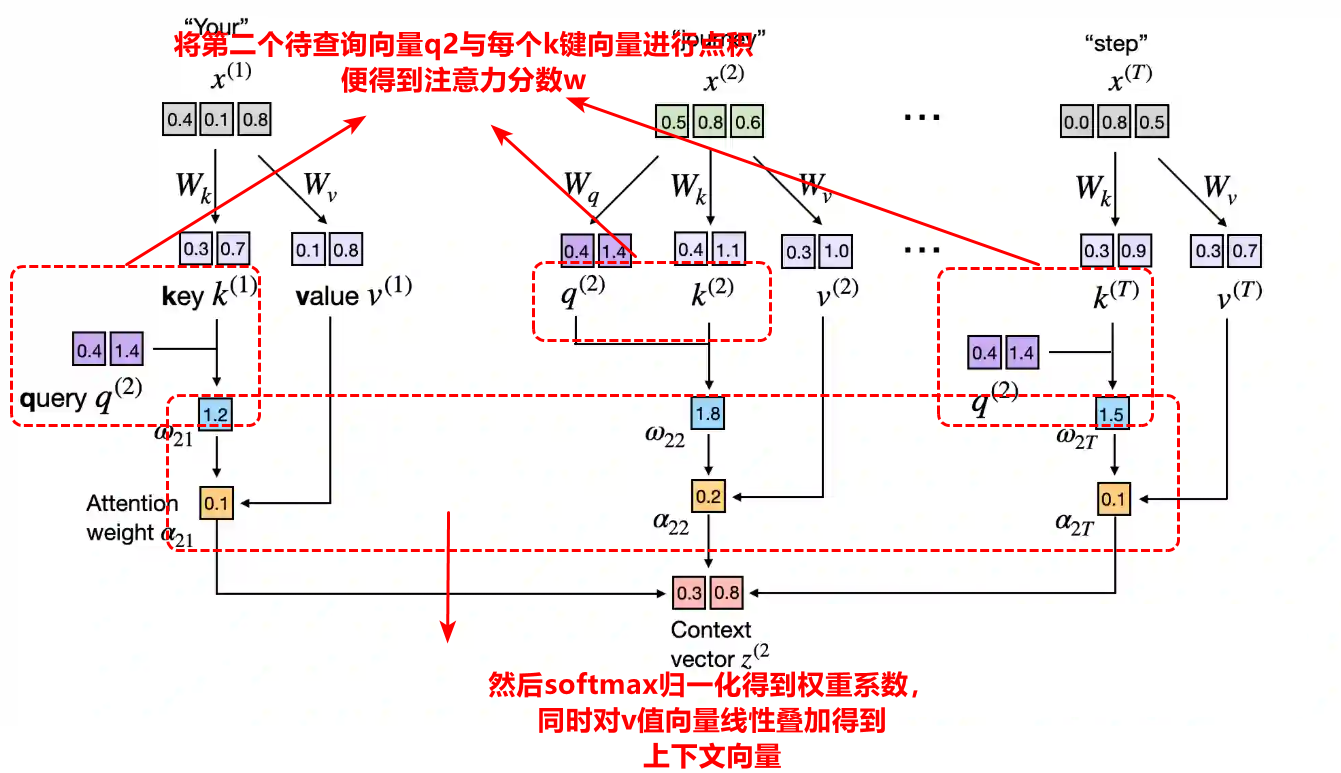
最后，用权重系数对每个token的值向量进行线性叠加就能得到上下文向量，这个上下文向量能够动态理解语义，因为Wq,Wk,Wv是动态训练可更新得到的。
总的来说，上面最后的公式可以总结为：
$Attention(Q,K,V)=softmax(QKTdk)VAttention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_{k}}})V$
以下是相关步骤的简练总价：
引入可训练权重矩阵，Wq,Wk,Wv。
1.对当前位置的词元嵌入向量分别与Wq,Wk,Wv相乘得到q,k,v，拿着这个当前位置的q，所有位置的k向量分别相乘，得到权重系数
2.对权重系数进行softmax归一化处理
3.用权重系数对所有v向量进行加权求和得到该位置的上下文向量，依次类推，计算所有上下文向量。
相关代码如下：

#%% 带训练权重的自注意力机制
import torch
import torch.nn.functional as F #该类提供了卷积，池化，激活等函数
# 假设对应词序列的token对应的词元嵌入向量为下面张量所示
inputs = torch.tensor([[0.43, 0.15, 0.89], # Your     (x^1)[0.55, 0.87, 0.66], # journey  (x^2)[0.57, 0.85, 0.64], # starts   (x^3)[0.22, 0.58, 0.33], # with     (x^4)[0.77, 0.25, 0.10], # one      (x^5)[0.05, 0.80, 0.55]] # step     (x^6)
)
torch.manual_seed(123)#设置随机种子，确保重复实验能够产生相同的效果
# 初始化Wq,Wk,Wv权重矩阵
Wq_matrix = torch.nn.Parameter(torch.rand(3, 2), requires_grad=False) #假设权重矩阵是3x2
Wk_matrix = torch.nn.Parameter(torch.rand(3, 2), requires_grad=False)
Wv_matrix = torch.nn.Parameter(torch.rand(3, 2), requires_grad=False)
# 计算所有token构成的q,k,v矩阵,所有嵌入词元向量矩阵inputs与权重矩阵对应矩阵相乘
q = torch.matmul(inputs, Wq_matrix)
k = torch.matmul(inputs, Wk_matrix)
v = torch.matmul(inputs, Wv_matrix)
# 结合注意力的计算公式
context_vector = torch.matmul(F.softmax(torch.matmul(q, k.T) / torch.sqrt(torch.tensor(k.shape[1])), dim=-1), v)

为了后续的方便，同时考虑到nn.Linear相比于nn.Parameter，提供了优化的初始化方案，在模型上定义了一个抽象的层：

#%% 带训练权重的自注意力机制的抽象类
import torch
import torch.nn.functional as F #该类提供了卷积，池化，激活等函数
class SelfAttention(nn.Module):def __init__(self,d_in=3,d_out=2,qkv_vias=False):super().__init__() #继承神经网络# Wq,Wk,Wv的初始化self.Wq_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.Wk_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.Wv_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵def foward(self,inputs):#前向传播计算q,k,vq = self.Wq_matrix(inputs) #inputs 与 Wq_matrix矩阵相乘k = self.Wk_matrix(inputs)  # inputs 与 Wk_matrix矩阵相乘v = self.Wv_matrix(inputs)  # inputs 与 Wv_matrix矩阵相乘attention_scores = q @ k.T # 注意力分数attention_weights = torch.softmax(attention_scores / k.shape()**0.5,dim=1) #softmax归一化权重系数context_vec_matrix = attention_weights @ v #线性叠加求上下文向量矩阵return context_vec_matrix

5 利用因果注意力隐藏未来词汇

权重系数矩阵右上角进行遮挡，然后归一化，使用dropout随机丢弃(随机置零)，防止过拟合。
事实上，考虑到逻辑的时空的连贯性，我们说话的时候是因果关系的，比如当我心里想说“我很想吃西瓜”，但是当我说出“我很想…”的时候，后续的的词你是不知道的，这就是因果关系，只知道当前及过去，当前的词是“想”，过去的词是“我很”，所以理论上来说，对于“我很想吃西瓜”这句话，应该逐个词掩码，说==“我”的时候，掩码”很想吃西瓜“,当说”我很“的时候，掩码”想吃西瓜“==，依次类推，所以因果注意力的本质上是更接近真实自然的真实语境，基于此，事实上我们只要基于可训练权重自注意力机制上，对softmax归一化权重矩阵进行上面部分掩码，然后重新归一化计算系数。
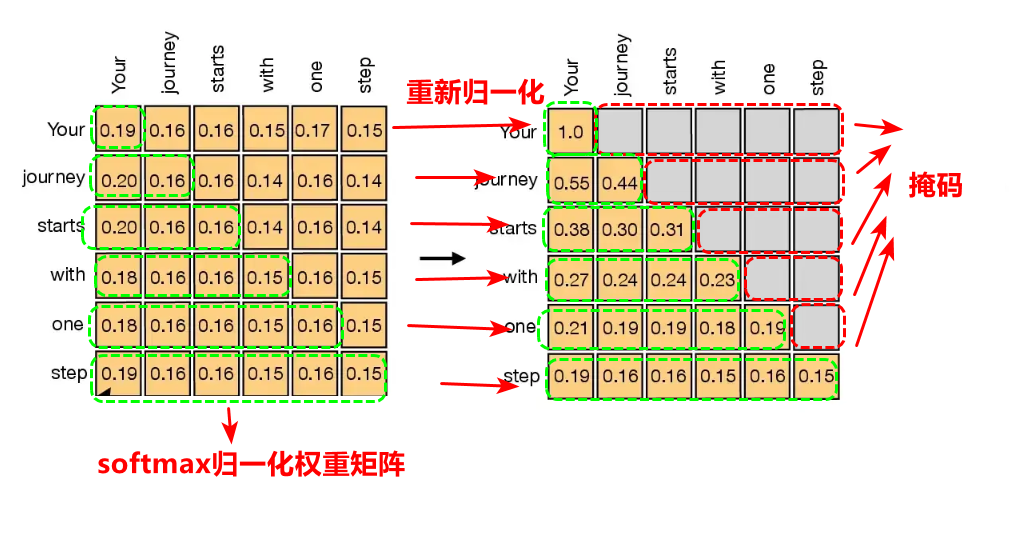
在这里插入图片描述
考虑采用的思路是创建上三角不包含对角线的上三角块，对权重系数矩阵的上三角部分掩码为 $−∞-\infty$ ,这样再次归一化的时候，由于 $e−∞e^{-\infty}$ 为零，就能实现因果+带训练权重的注意力机制，其相关代码如下：

#%% 掩码+带训练权重的自注意力机制的抽象类
import torch
import torch.nn.functional as F #该类提供了卷积，池化，激活等函数
class SelfAttention(nn.Module):def __init__(self,d_in=3,d_out=2,qkv_vias=False):super().__init__() #继承神经网络# Wq,Wk,Wv的初始化self.Wq_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.Wk_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.Wv_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵def foward(self,inputs):#前向传播计算q,k,vq = self.Wq_matrix(inputs) #inputs 与 Wq_matrix矩阵相乘k = self.Wk_matrix(inputs)  # inputs 与 Wk_matrix矩阵相乘v = self.Wv_matrix(inputs)  # inputs 与 Wv_matrix矩阵相乘attention_scores = q @ k.T # 注意力分数attention_weights = torch.softmax(attention_scores / k.shape()**0.5,dim=1) #softmax归一化权重系数mask = torch.triu(torch.ones(6,6),diagonal=1)#上三角(不包含对角线)矩阵创建masked = attention_weights.masked_fill(mask.bool(),-torch.inf)#对矩阵中为1的上半部分不包含对角线进行掩码为-infattention_weights = torch.softmax(masked/k.shape()**0.5,dim=-1)#再次使用softmax归一化context_vec_matrix = attention_weights @ v #线性叠加求上下文向量矩阵return context_vec_matrix

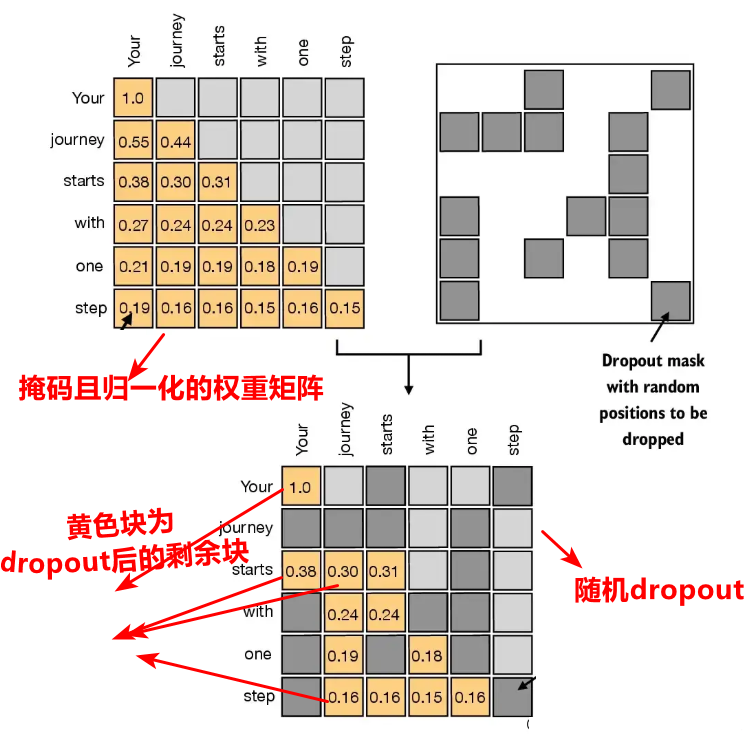
在这里插入图片描述

为了防止过拟合，也就是数据只在训练集上表现较好的效果，事实上是模型过于复杂，举个简单列子来理解，就好比原来是三次函数的趋势，你要了7次函数，虽然也可以拟合训练集，但是模型更加复杂了，这样预测的时候，容易陷入局部更加详细的部分，为了解决这个问题，使用了dropout来随机丢弃权重矩阵系数中的部分系数，或者说叫置零，通常设置随机丢弃率来合理调整丢弃的比列，以下是增加了dropout后的代码：

#%% dropout掩码+带训练权重的自注意力机制的抽象类
import torch
import torch.nn.functional as F #该类提供了卷积，池化，激活等函数
class SelfAttention(nn.Module):def __init__(self,d_in=3,d_out=2,qkv_vias=False):super().__init__() #继承神经网络# Wq,Wk,Wv的初始化self.Wq_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.Wk_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.Wv_matrix = nn.Linear(d_in, d_out, bias=qkv_vias) #3x2全连接层的抽象层,默认会有一个初始化权重矩阵self.dropout = nn.Dropout(0.1) #dropout随机丢弃10%def foward(self,inputs):#前向传播计算q,k,vq = self.Wq_matrix(inputs) #inputs 与 Wq_matrix矩阵相乘k = self.Wk_matrix(inputs)  # inputs 与 Wk_matrix矩阵相乘v = self.Wv_matrix(inputs)  # inputs 与 Wv_matrix矩阵相乘attention_scores = q @ k.T # 注意力分数attention_weights = torch.softmax(attention_scores / k.shape()**0.5,dim=1) #softmax归一化权重系数mask = torch.triu(torch.ones(6,6),diagonal=1)#上三角(不包含对角线)矩阵创建masked = attention_weights.masked_fill(mask.bool(),-torch.inf)#对矩阵中为1的进行掩码为-infattention_weights = torch.softmax(masked/k.shape()**0.5,dim=-1)#再次使用softmax归一化attention_weights = self.dropout(attention_weights)  # 先对归一化得权重系数进行随机丢弃dropout，防止过拟合context_vec_matrix = attention_weights @ v #线性叠加求上下文向量矩阵return context_vec_matrix

6 将单头注意力扩展到多头注意力

将多个来源的上下文向量进行线性叠加。
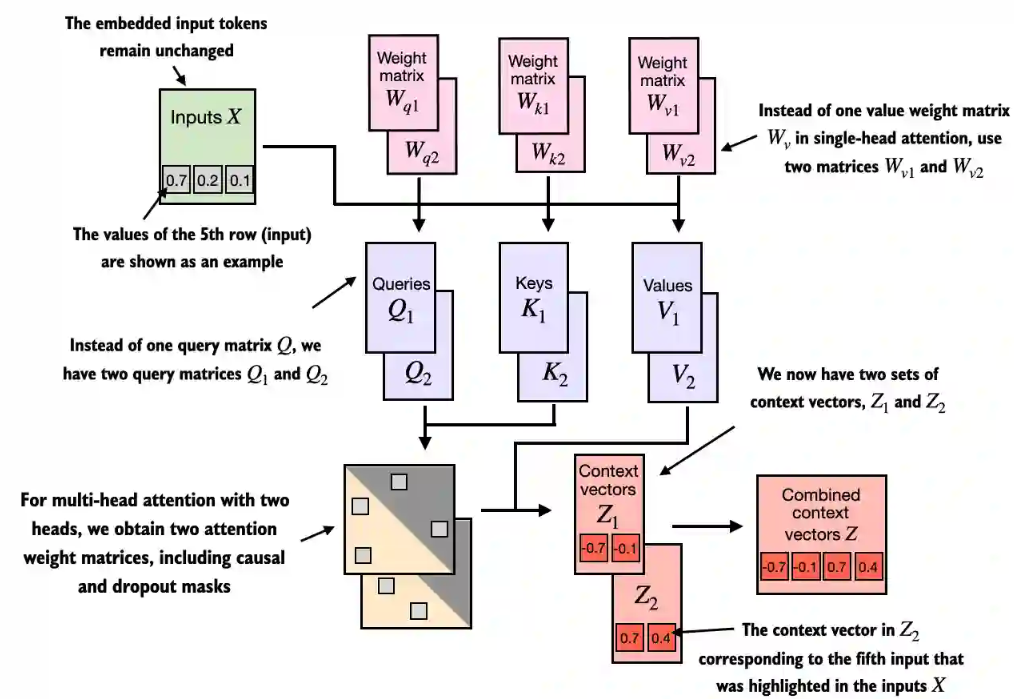
在这里插入图片描述

class MultiHeadAttention(nn.Module):def __init__(self, d_in, d_out, context_length, dropout, num_heads, qkv_bias=False):super().__init__()assert (d_out % num_heads == 0), \"d_out must be divisible by num_heads"self.d_out = d_outself.num_heads = num_headsself.head_dim = d_out // num_heads # Reduce the projection dim to match desired output dimself.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)self.out_proj = nn.Linear(d_out, d_out)  # Linear layer to combine head outputsself.dropout = nn.Dropout(dropout)self.register_buffer("mask",torch.triu(torch.ones(context_length, context_length),diagonal=1))def forward(self, x):b, num_tokens, d_in = x.shape# As in `CausalAttention`, for inputs where `num_tokens` exceeds `context_length`, # this will result in errors in the mask creation further below. # In practice, this is not a problem since the LLM (chapters 4-7) ensures that inputs  # do not exceed `context_length` before reaching this forwarkeys = self.W_key(x) # Shape: (b, num_tokens, d_out)queries = self.W_query(x)values = self.W_value(x)# We implicitly split the matrix by adding a `num_heads` dimension# Unroll last dim: (b, num_tokens, d_out) -> (b, num_tokens, num_heads, head_dim)keys = keys.view(b, num_tokens, self.num_heads, self.head_dim) values = values.view(b, num_tokens, self.num_heads, self.head_dim)queries = queries.view(b, num_tokens, self.num_heads, self.head_dim)# Transpose: (b, num_tokens, num_heads, head_dim) -> (b, num_heads, num_tokens, head_dim)keys = keys.transpose(1, 2)queries = queries.transpose(1, 2)values = values.transpose(1, 2)# Compute scaled dot-product attention (aka self-attention) with a causal maskattn_scores = queries @ keys.transpose(2, 3)  # Dot product for each head# Original mask truncated to the number of tokens and converted to booleanmask_bool = self.mask.bool()[:num_tokens, :num_tokens]# Use the mask to fill attention scoresattn_scores.masked_fill_(mask_bool, -torch.inf)attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)attn_weights = self.dropout(attn_weights)# Shape: (b, num_tokens, num_heads, head_dim)context_vec = (attn_weights @ values).transpose(1, 2) # Combine heads, where self.d_out = self.num_heads * self.head_dimcontext_vec = context_vec.contiguous().view(b, num_tokens, self.d_out)context_vec = self.out_proj(context_vec) # optional projectionreturn context_vectorch.manual_seed(123)batch_size, context_length, d_in = batch.shape
d_out = 2
mha = MultiHeadAttention(d_in, d_out, context_length, 0.0, num_heads=2)context_vecs = mha(batch)print(context_vecs)
print("context_vecs.shape:", context_vecs.shape)

7 Pytorch附录

7.1 torch.nn.Linear

定义了一个全连接层，torch.nn.Linear(in_features,out_features,bias)
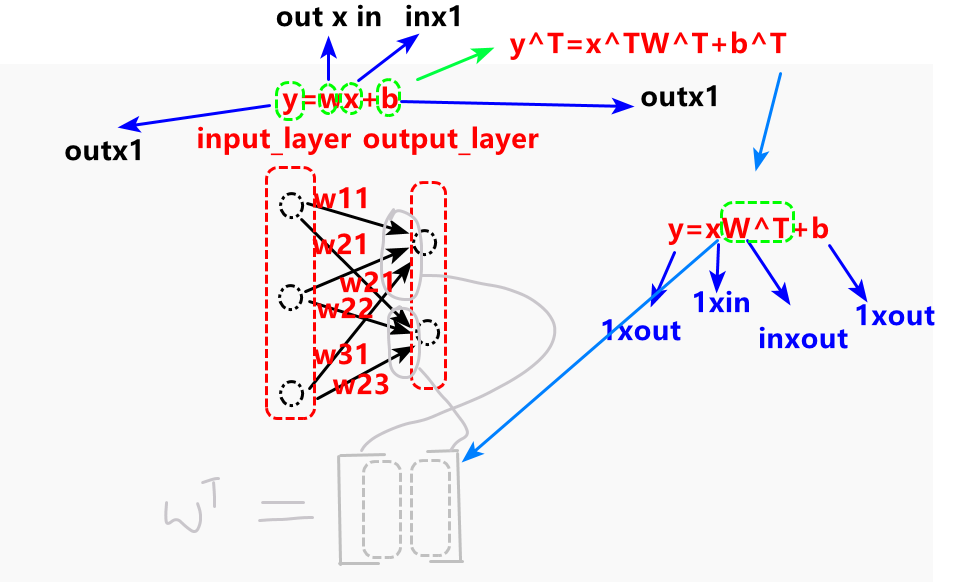
在这里插入图片描述
torch.nn.Linear(in_features,out_features,bias)是一个抽象全连接神经网络层，输入x，经过 $y=xw^{T}+b$ ，输出y，特别地当偏置项为0的时候 $y=xw^{T}$ ,事实上就是一个矩阵的乘法，输入x与 $w^{T}$ 相乘，而当这个抽象全连接神经网络层被定义的时候，权重矩阵 $w^{T}$ 以及偏置项b就会自动初始化。