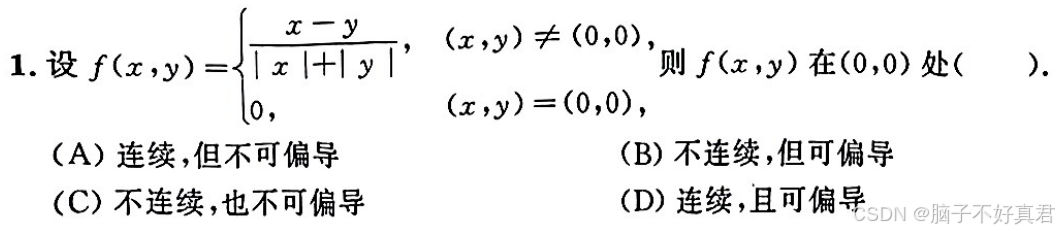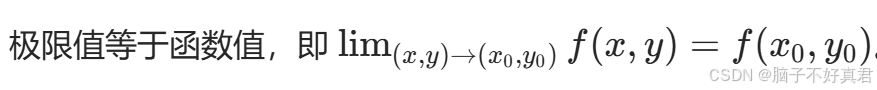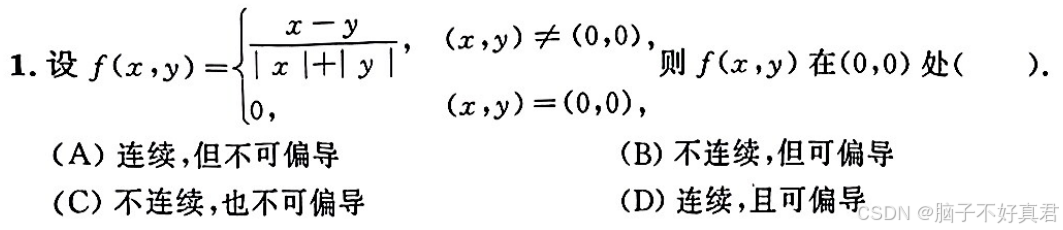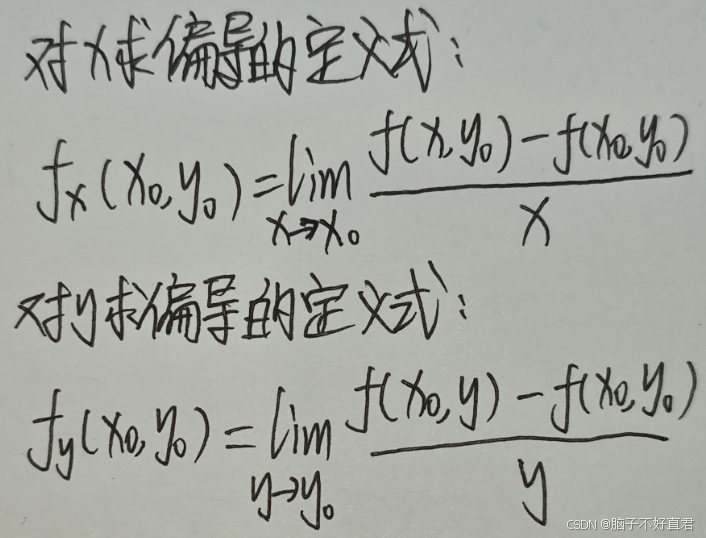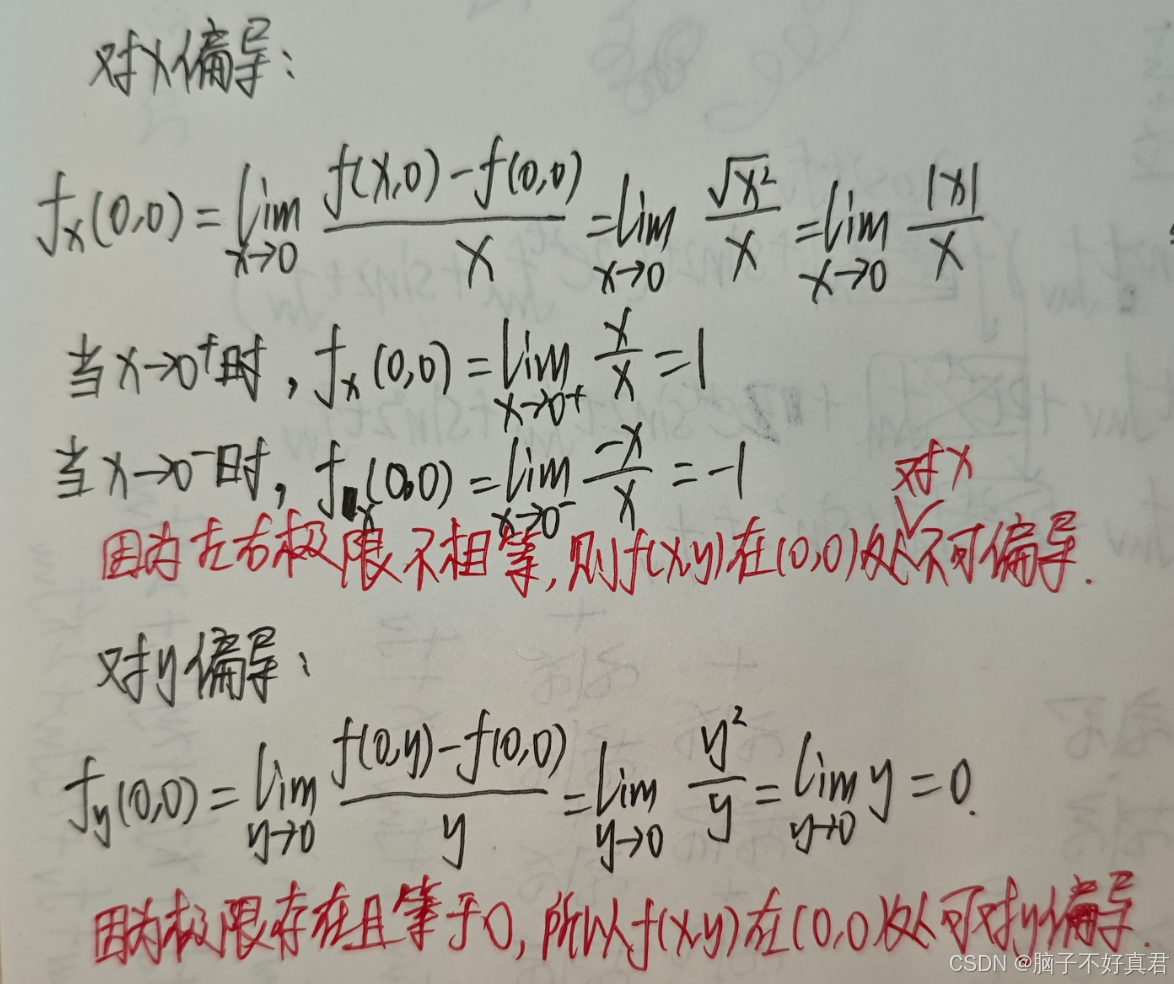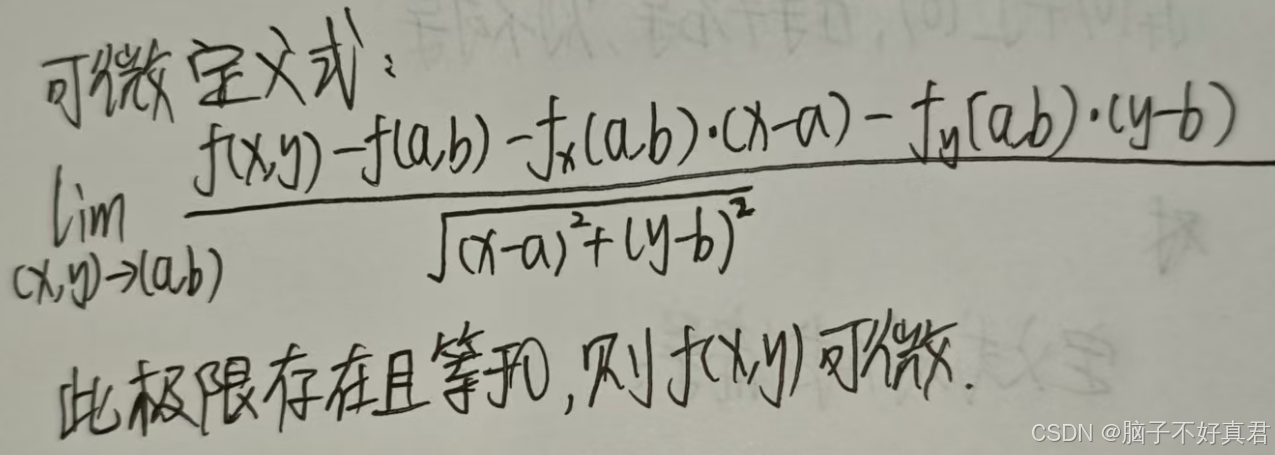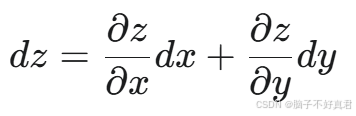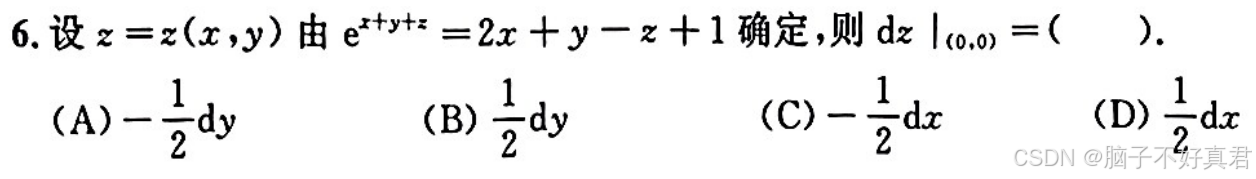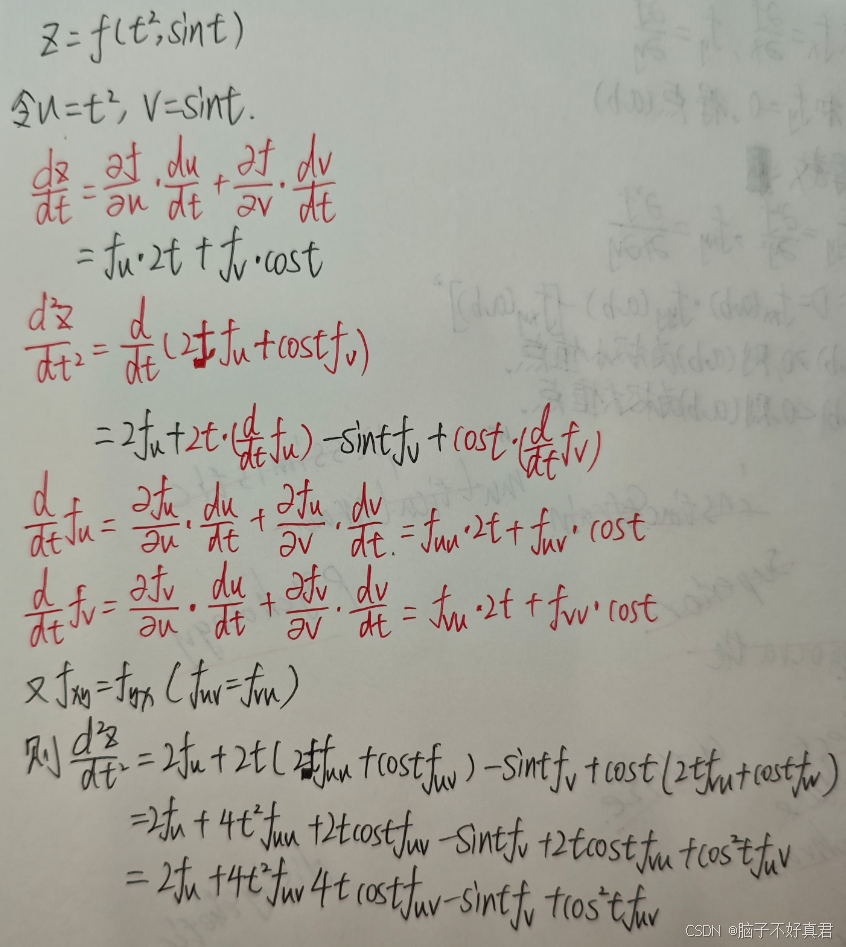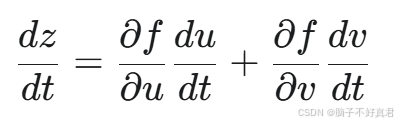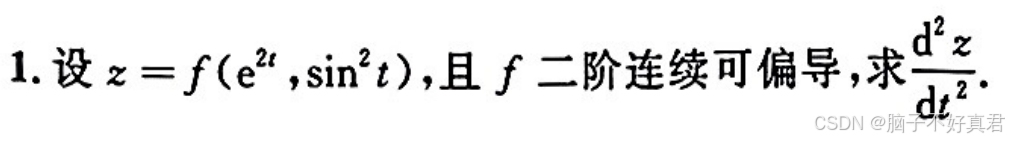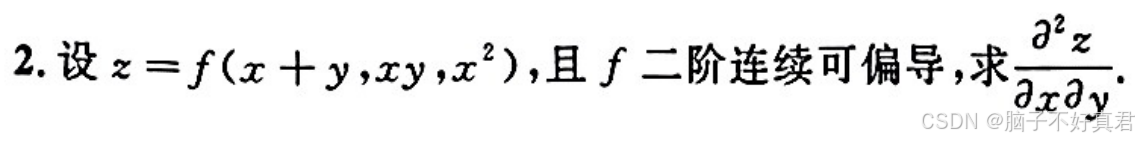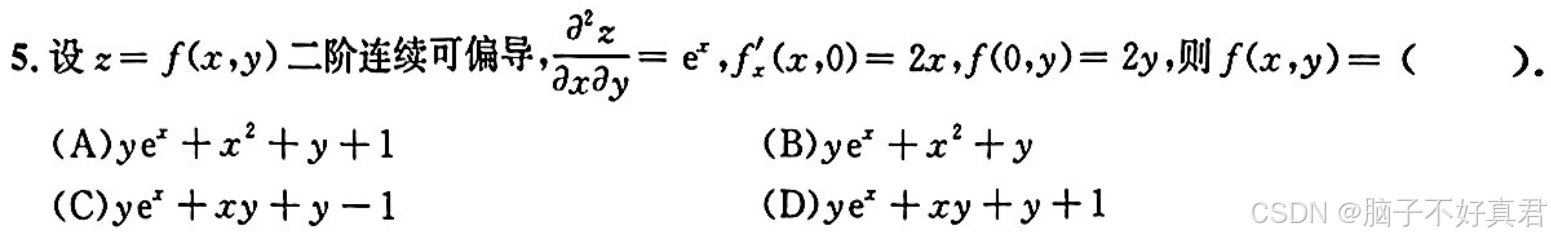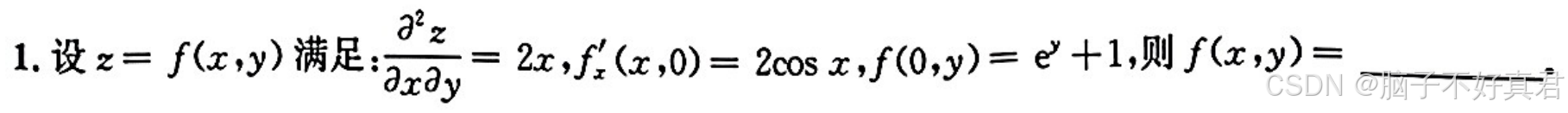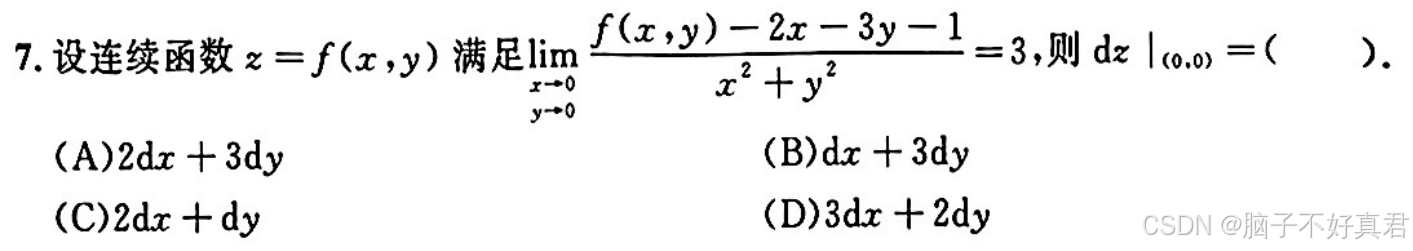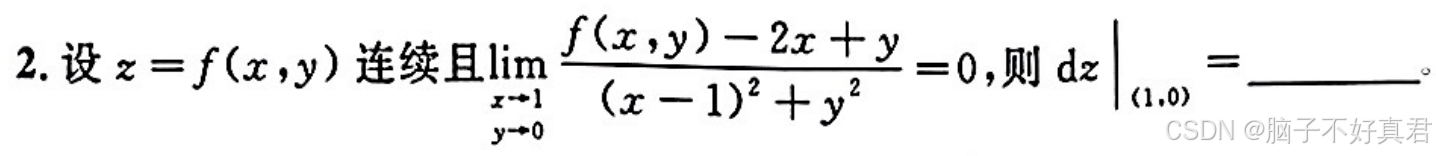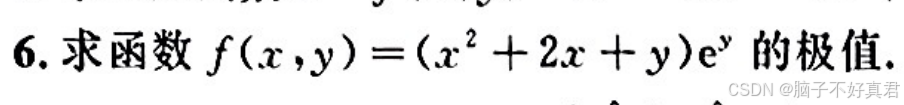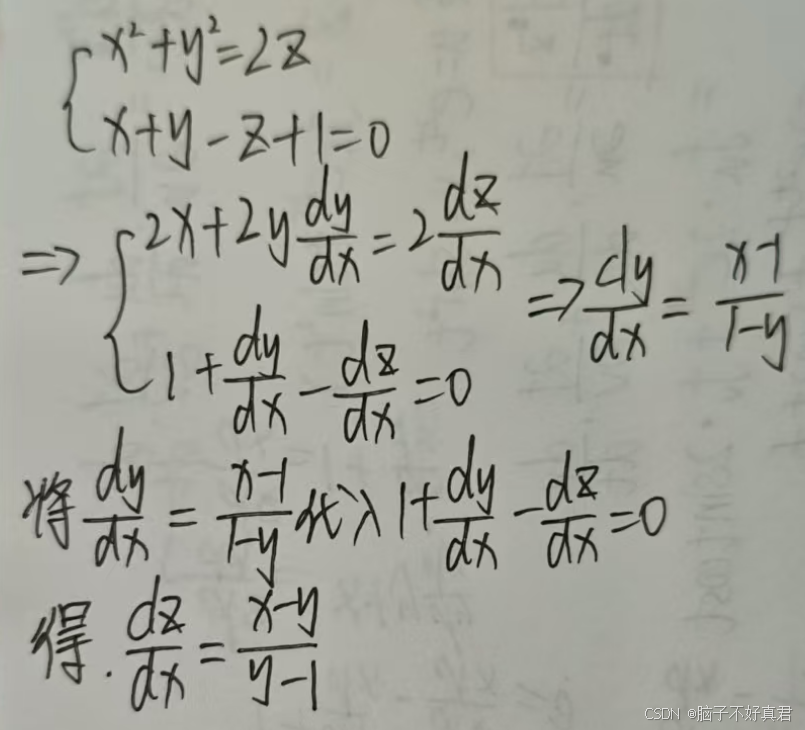一文速通《多元函数微分学》
目录
一、解题必背知识点
(1)二元函数连续、可偏导、可微之间的关系
例题
(2)判断二元函数的连续性
(3)判断极限存在的方法
方法①:直接代入法
方法②:路径法(常用)
例题
(4)判断二元函数的可偏导性
偏导数的定义公式法:
例题
(5)判断二元函数的可微性
(6)f(x)=|x|在 x=0 点是不可导的(图像上是一个尖点)
(7)隐函数求导
例题
(8)全微分公式
例题
(9)二元函数极值求法
例题
(10)克莱罗定理
例题
(11) 全导数公式
例题
(12)三元函数求二阶偏导
例题
(13)隐函数存在定理
例题
(14)二元函数连续性、偏导性、可微性判断的综合例题
例题
二、解题必备技巧
(1)偏导+积分的——一种题型
(2)题目所给极限存在,且极限分母→0,为保证极限存在,分子必须→0或某种形式(具体看题目),利用分子→或某种形式(具体看题目),可以求得解题需要的信息.
例题
(3)在求二元函数的极值点的临界点时,如果在解 fy=0 中含有 x,可直接代入在解 fx=0 中得到的x,从而求得 y.
例题
(4)读懂 y=y(x),z=z(x)
例题
(5)极坐标在求二元函数极限中的应用
例题
(6)二元函数连续性、偏导性、可微性判断的综合例题
例题
一、解题必背知识点
(1)二元函数连续、可偏导、可微之间的关系
可微 => 连续 => 极限存在.
可微 => 可偏导.
连续 不一定 可微.
可偏导 不一定 连续,更不一定 可微.例题
(2)判断二元函数的连续性
一个二元函数 f(x,y) 在点 (x0,y0) 处连续,需要满足以下三个条件:
(3)判断极限存在的方法
方法①:直接代入法
极限值等于函数值则函数连续,又连续 => 极限存在,则极限存在.
方法②:路径法(常用)
二元函数极限存在,要求点 (x,y) 沿任何路径趋近于 (x0,y0) 时,极限值都存在且相等。反之,如果能找到至少两条路径,使得极限值不相等,那么极限不存在,从而函数不连续。
例题
(4)判断二元函数的可偏导性
偏导数的定义公式法:
注意:左右偏导定义式存在即可偏导,不需要相等. 只要有一个偏导数不存在或不可偏导,函数在该点就是不可偏导的.例题
(5)判断二元函数的可微性
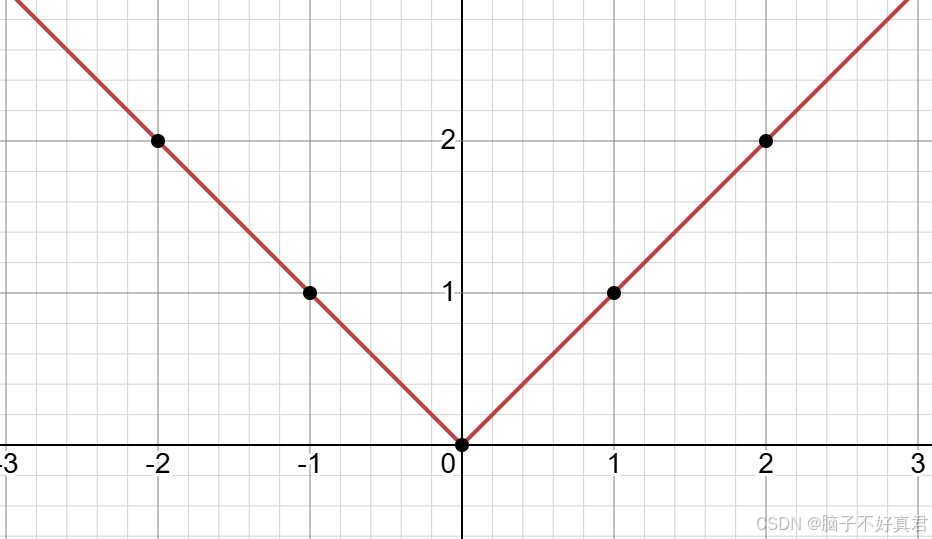
(6)f(x)=|x|在 x=0 点是不可导的(图像上是一个尖点)
几何直观:尖点处无法画出唯一的切线
代数证明:左右导数不相等
(7)隐函数求导
隐函数求导基本思路是:直接对方程两边分别对自变量求偏导,不需要对方程进行移项到一端只剩z.
例题
(8)全微分公式
例题
(9)二元函数极值求法
例题
(10)克莱罗定理
例题
(11) 全导数公式
例题
(12)三元函数求二阶偏导
例题
(13)隐函数存在定理
例题
(14)二元函数连续性、偏导性、可微性判断的综合例题
例题
二、解题必备技巧
(1)偏导+积分的——一种题型
(2)题目所给极限存在,且极限分母→0,为保证极限存在,分子必须→0或某种形式(具体看题目),利用分子→或某种形式(具体看题目),可以求得解题需要的信息.
这个技巧会以意想不到的形式出现.
例题
(3)在求二元函数的极值点的临界点时,如果在解 fy=0 中含有 x,可直接代入在解 fx=0 中得到的x,从而求得 y.
例题
(4)读懂 y=y(x),z=z(x)
例题
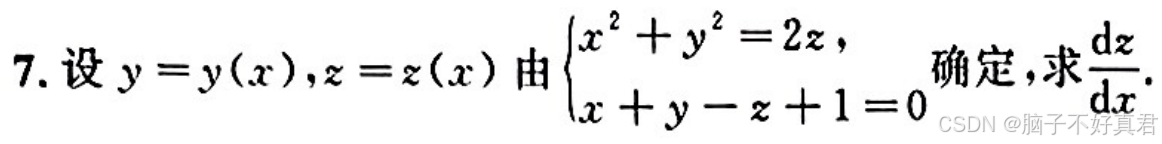
(5)极坐标在求二元函数极限中的应用
例题
(6)二元函数连续性、偏导性、可微性判断的综合例题
例题