机器学习(重学版)基础篇(概念与评估)
本篇参考周志华老师的西瓜书,但是本人学识有限仅能理解皮毛,如有错误诚请读友评论区指正,万分感谢。
一、基础概念与评估方法
本节目标:建立理论基础框架
1、机器学习定义
机器学习是一门通过计算手段利用经验(以数据形式存在)改善系统性能的学科。其核心是研究 “学习算法”—— 通过该算法,输入经验数据可生成 “模型”,模型能对新情况(如未见过的样本)做出判断。
形式化定义:若计算机程序通过经验 E,在任务类 T 上的性能(以 P 评估)得到改善,则称该程序对 E 进行了学习。
我的理解:
机器学习是让计算机从数据中自动学习规律(模型),从而提升其完成特定任务(如预测、识别)能力的技术。
六维核心要点:
目标: 改善系统在特定任务上的性能
手段: 利用计算处理数据(经验)
核心: 学习算法
产物: 模型
关键能力: 模型能对新情况(未见过的数据)做出有效判断(泛化能力)
衡量: 性能指标(P)的提升
数据 -> 算法 -> 模型 -> 预测 -> 提升
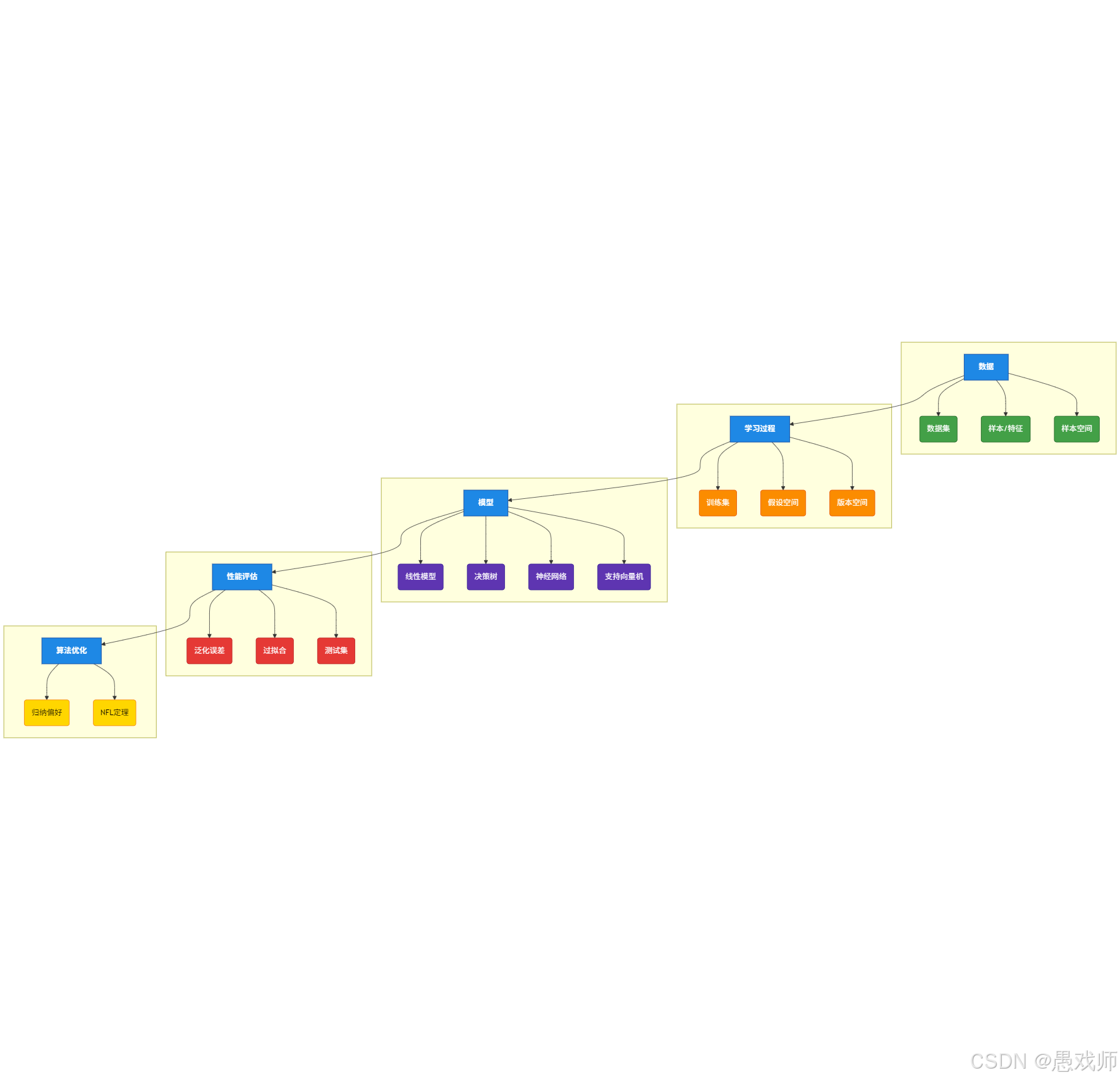 2、核心术语
2、核心术语
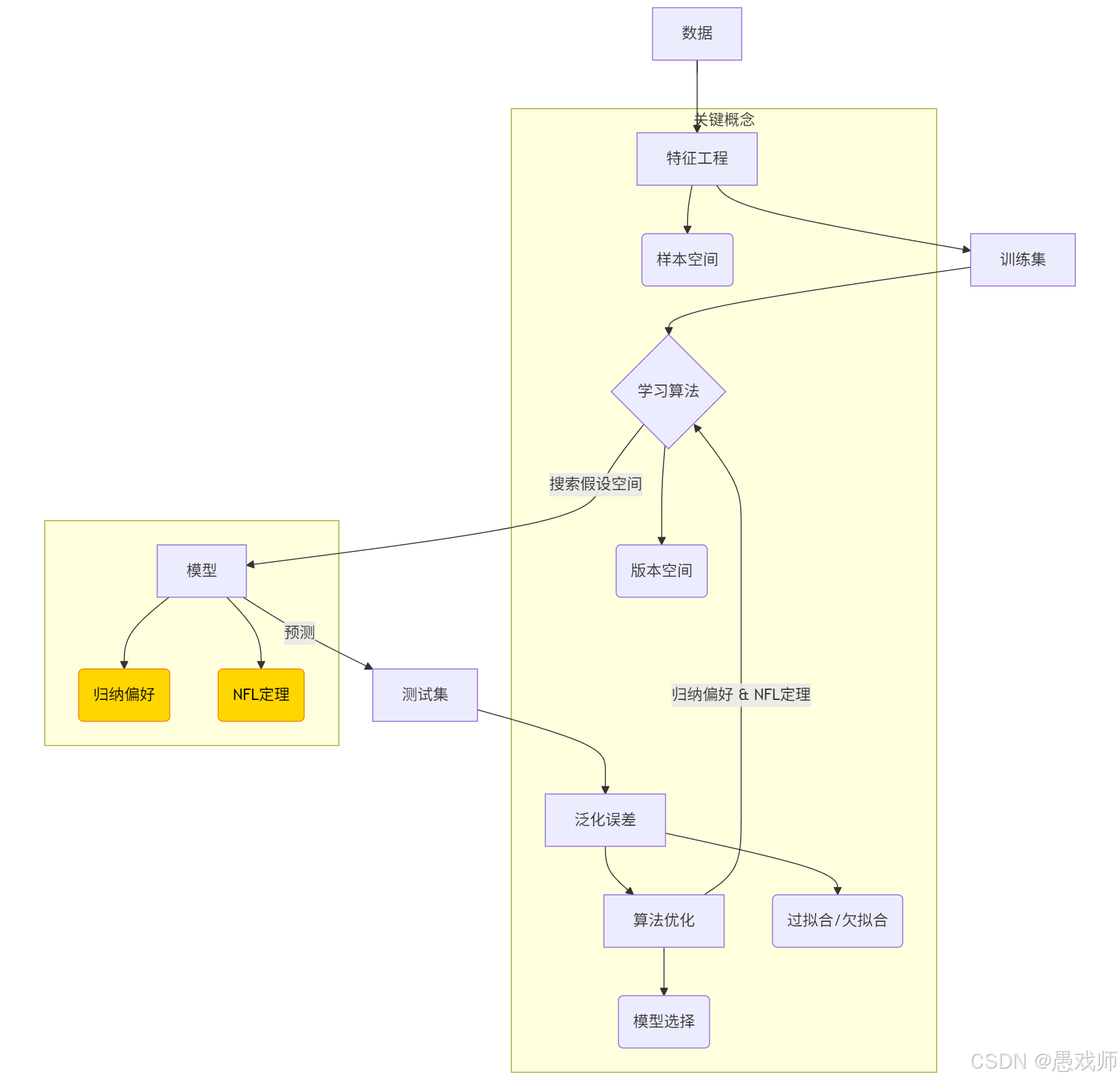
2.1、基础概念与数据术语
机器学习(Machine Learning, ML)
通过计算手段利用数据(经验)改善系统性能的学科,核心是从数据中生成模型的学习算法。
示例:用历史房价数据训练模型预测新房价。数据集(Data Set)
多条记录组成的集合,每条记录描述一个对象或事件。
示例:1000条西瓜的{色泽, 根蒂, 敲声, 标签}记录。样本/示例(Sample/Instance)
数据集中的单条记录(如一条西瓜数据)。
样例(Example):带标记(Label)的样本(如标注"好瓜"的西瓜数据)。特征/属性(Feature/Attribute)
描述样本的维度(如西瓜的"色泽"),其取值称属性值(Attribute Value)(如"青绿")。
样本空间(Sample Space)
所有特征张成的多维空间,每个样本是空间中的一个点(即特征向量)。
示例:用[色泽, 根蒂, 敲声]构建三维空间,每个西瓜对应一个坐标点。
2.2、学习过程术语
训练(Training)
从数据中学习模型的过程,核心是通过算法发现数据内在规律。
训练集(Training Set):用于训练模型的数据集合(如80%的西瓜数据)
训练样本(Training Sample):训练集中的单条数据记录(如一条西瓜的{色泽=青绿, 根蒂=蜷缩, 标签=好瓜})
示例:用1000条历史病例训练疾病诊断模型
假设(Hypothesis)
模型对数据规律的推测(如“根蒂蜷缩的西瓜是好瓜”),目标是逼近真相(Ground-Truth)(客观规律)。
模型是假设的形式化表达,学习本质是寻找最佳假设标记(Label)
样本的预测目标值(监督学习的核心),又称标签。
分类任务:离散值(如“好瓜/坏瓜”)
回归任务:连续值(如西瓜价格15.6元)
带标记的样本称为 样例(Example)
假设空间(Hypothesis Space)
所有可能假设的集合,反映问题的求解范围。
示例:西瓜分类问题中,所有由“色泽/根蒂/敲声”组合构成的判断规则
数学表达:若特征有3个二值属性,假设空间大小为 223=256223=256 种可能规则
版本空间(Version Space)
假设空间中与训练集一致的假设子集(即符合所有训练样本的假设)。
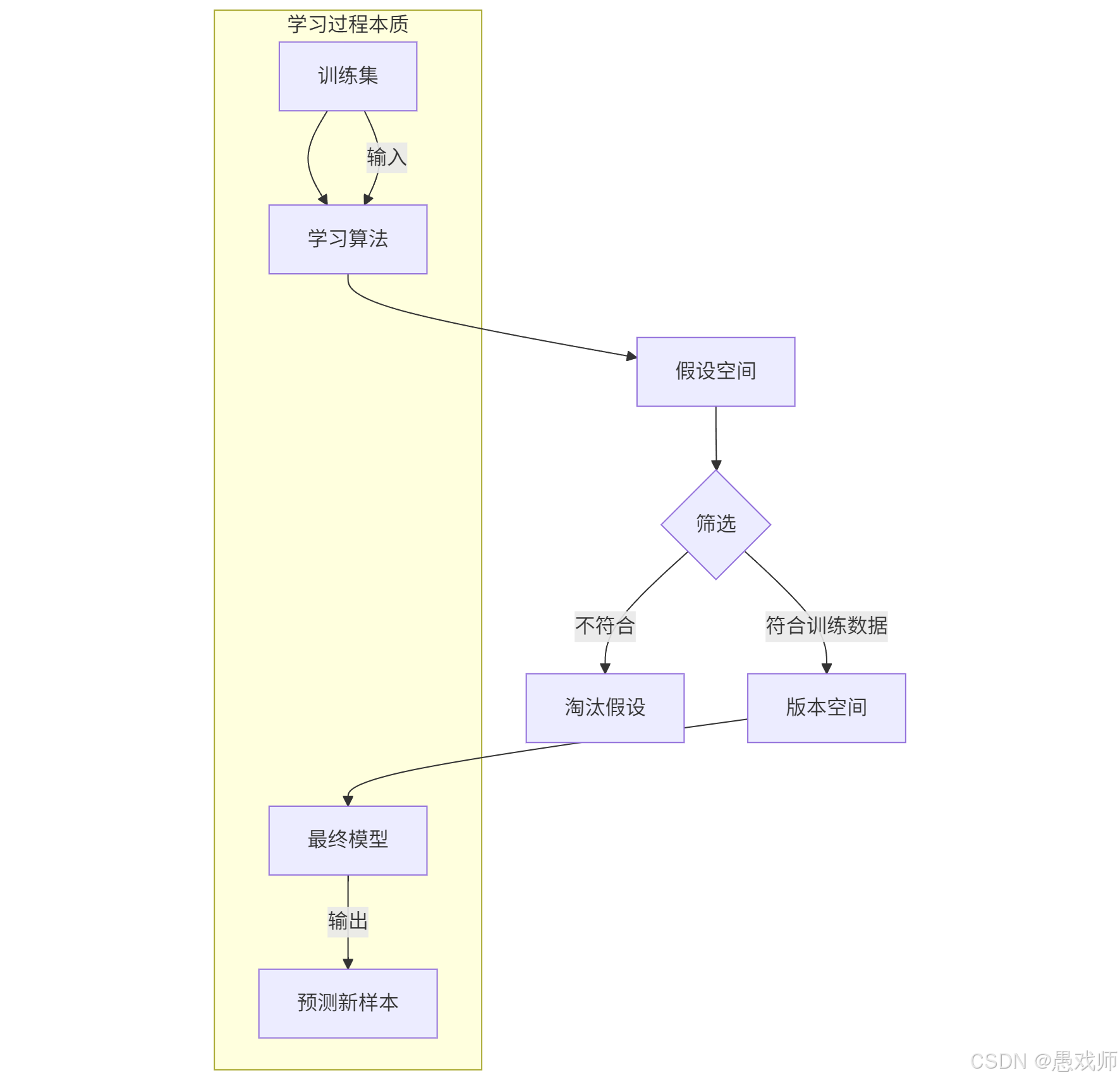
举个例子:(西瓜分类)
训练集
样本1:{色泽=青绿, 根蒂=蜷缩, 敲声=浊响, 标签=好瓜}
样本2:{色泽=乌黑, 根蒂=稍蜷, 敲声=沉闷, 标签=坏瓜}
假设空间
假设1:根蒂=蜷缩 → 好瓜
假设2:色泽=青绿 AND 敲声=浊响 → 好瓜
版本空间生成
若假设1能正确分类所有训练样本 → 进入版本空间
若假设2将样本2误分类 → 被淘汰
最终模型
从版本空间中根据归纳偏好选择最优假设(如选择最简规则:“根蒂=蜷缩 → 好瓜”)
核心价值:版本空间缩小了搜索范围,使学习算法能高效找到可行解,但最终模型选择依赖算法偏好(如奥卡姆剃刀原则优先选择简单假设)。
2.3、性能评估术语
1. 误差(Error)
定义:模型预测结果与真实值之间的差异。
训练误差(Training Error):模型在训练集上的误差(反映模型对已知数据的拟合程度)。
泛化误差(Generalization Error):模型在新样本上的误差(反映模型的实际应用能力,核心优化目标)。
2. 泛化(Generalization)
定义:模型对未见过的数据的适应能力。
核心目标:最小化泛化误差(而非训练误差)。
示例:背熟100道题得满分(训练误差=0),但考试遇到新题不及格(泛化误差高)→ 泛化失败。
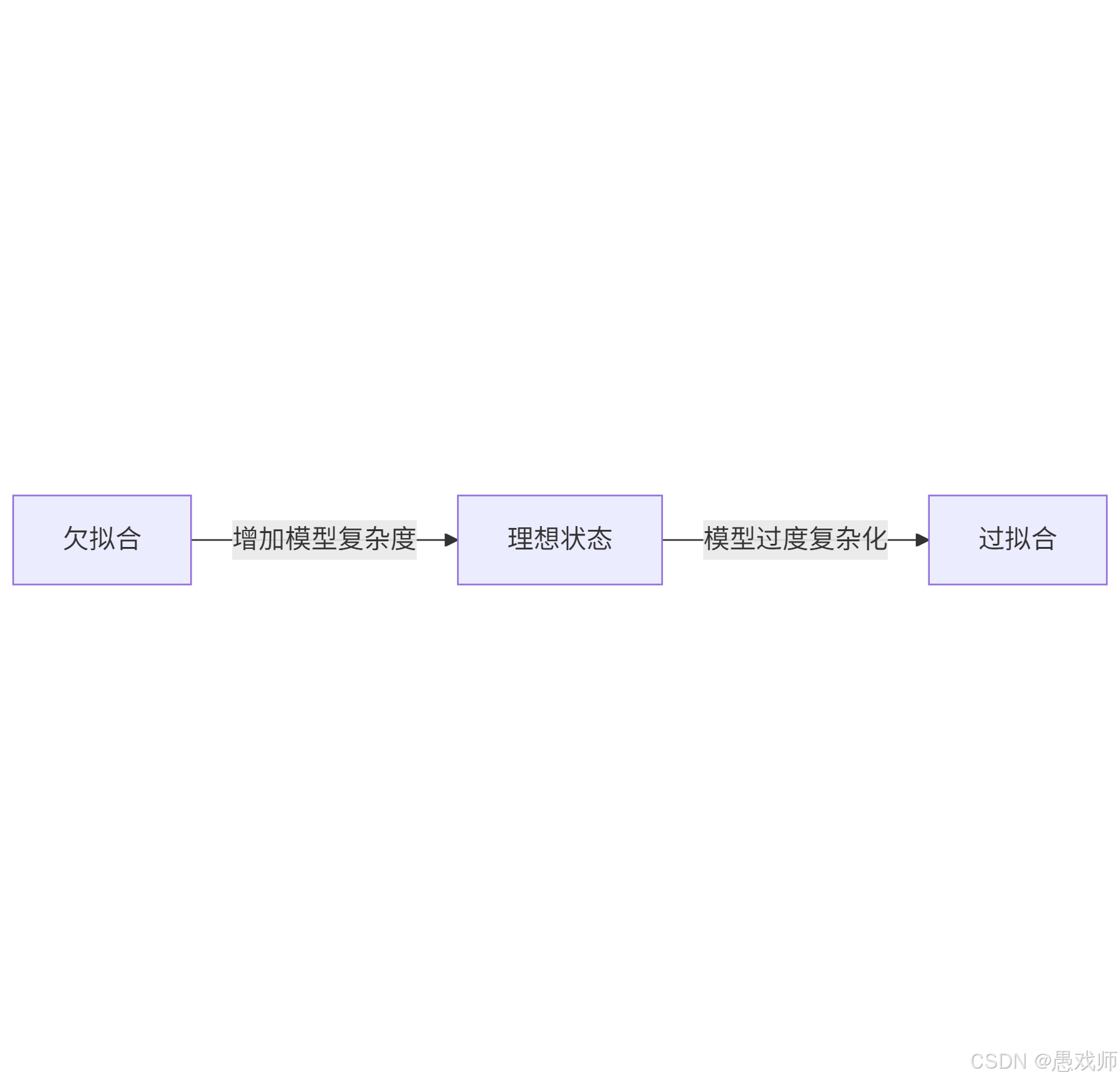
3. 过拟合(Overfitting) vs 欠拟合(Underfitting)
| 现象 | 本质原因 | 表现 | 解决方案 |
|---|---|---|---|
| 过拟合 | 模型过度复杂,拟合了训练数据中的噪声 | 训练误差极低,泛化误差高 | 正则化、增加数据量、简化模型 |
| 欠拟合 | 模型过于简单,未捕捉数据规律 | 训练误差和泛化误差均高 | 增加模型复杂度、特征工程 |
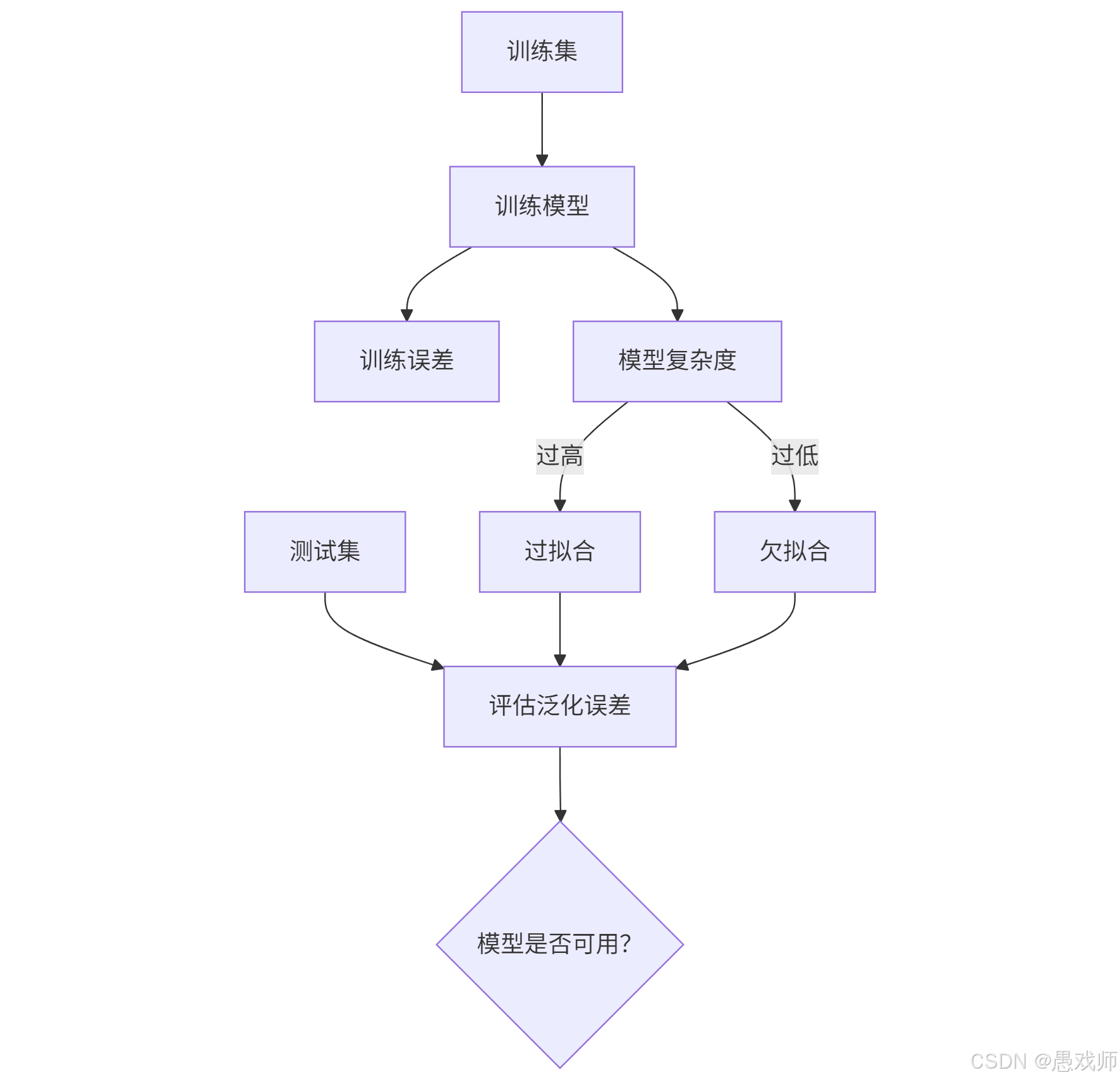
4. 测试集(Testing Set)
定义:用于最终评估模型泛化性能的独立数据集,必须与训练集完全互斥(无重叠样本)。
为什么需要?:防止模型通过“死记硬背”训练数据获得虚假高精度。
实践规则:
划分比例:常用 70% 训练集 / 30% 测试集
严格隔离:测试集样本绝不能参与训练过程
反例:若用全部数据训练和测试,模型可能100%准确但实际无法预测新样本。
2.4、算法哲学术语
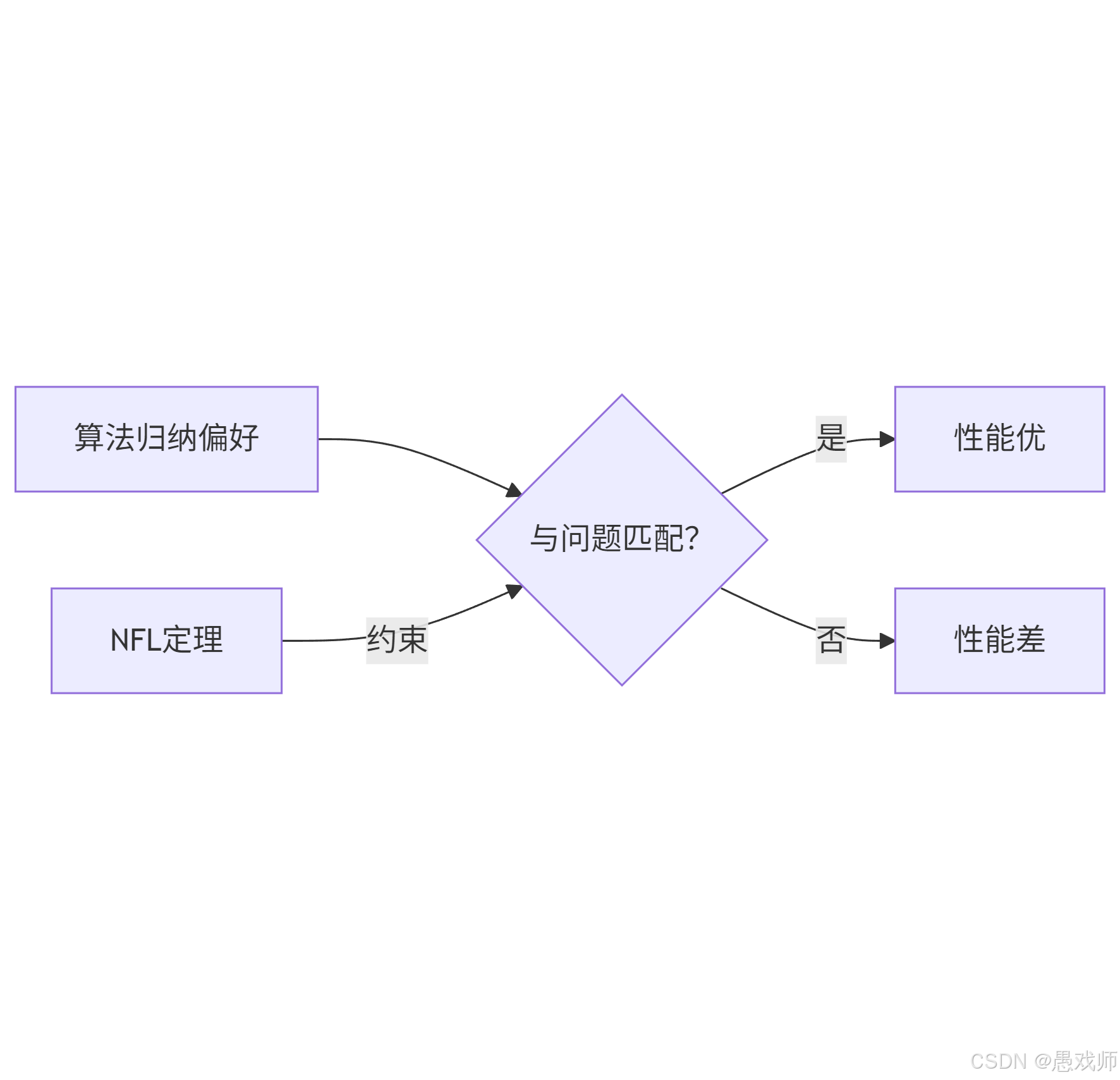
归纳偏好(Inductive Bias)
算法对特定假设的先天偏好(如决策树偏好"信息增益高的特征")。
NFL 定理(No Free Lunch Theorem)
核心:没有万能最优算法!脱离具体问题,所有算法期望性能相同。
启示:为图像识别选CNN,为表格数据选决策树。
2.5、经典算法术语
| Algorithm | Key Concept | Core Mechanism |
|---|---|---|
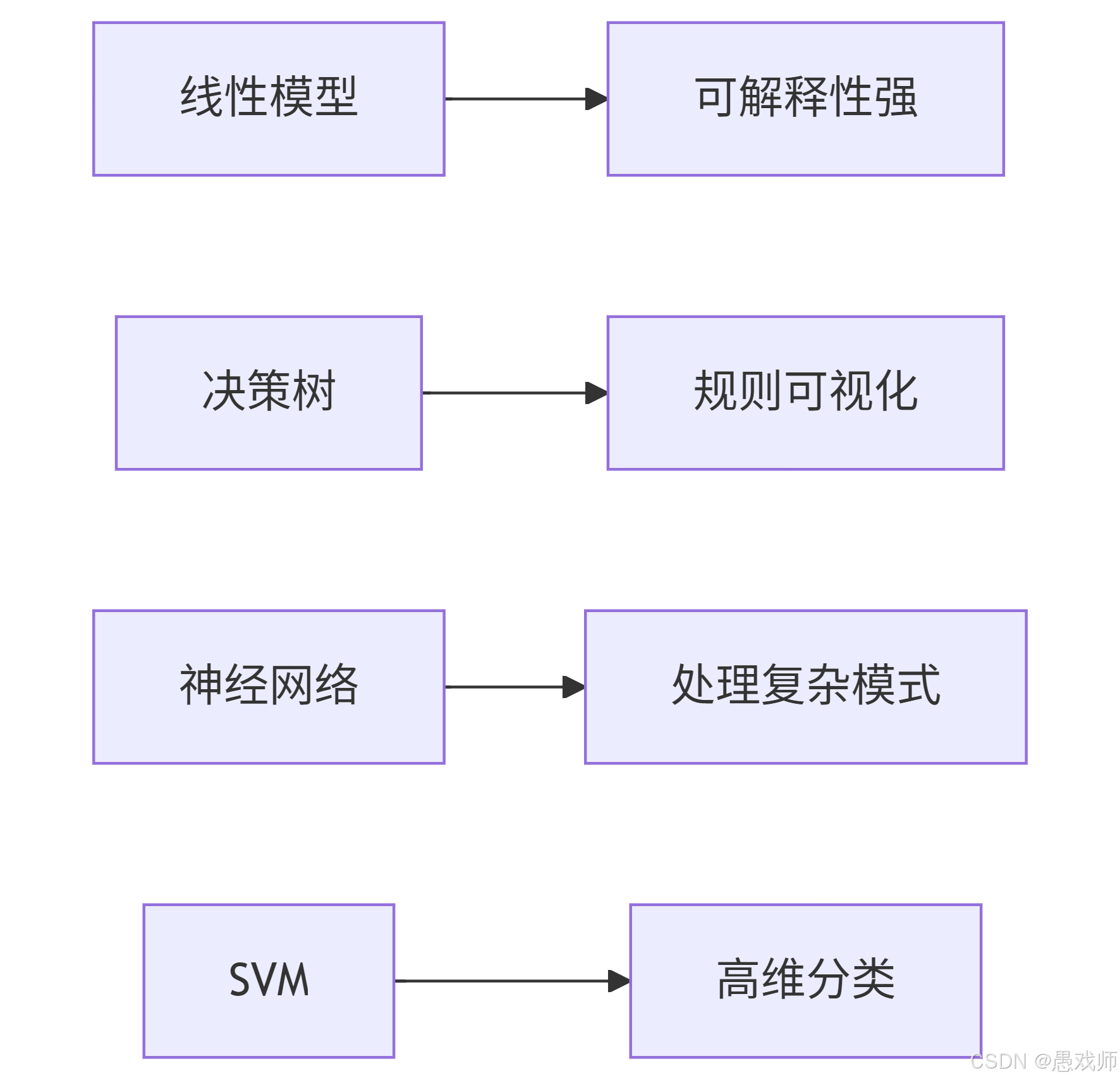
| 线性模型(Linear Model) | Interpretable linear combinations | |
| 决策树(Decision Tree) | Tree-structured attribute partitioning (e.g., color → stem → sound) | Splitting criteria (信息增益/Gini) |
| 神经网络(Neural Network) | Layered nonlinear transformations | 反向传播(Backpropagation, BP) |
| 支持向量机(Support Vector Machine, SVM) | Maximize-margin hyperplane | 核技巧(Kernel Trick)/支持向量(Support Vectors) |
3.归纳偏好与NFL定理
“没有最好的算法,只有最匹配问题的算法”
—— 通过分析数据分布、目标函数、误差容忍度,选择偏好与问题对齐的模型。
3.1、归纳偏好(Inductive Bias)
1. 核心内容
定义:算法对特定假设的固有偏好(如“简单模型优先”),是模型从版本空间中选择唯一解的必要条件。
必要性:
若无偏好,当多个假设与训练集一致时(如西瓜分类中“好瓜=根蒂蜷缩”和“好瓜=根蒂蜷缩且敲声浊响”),算法无法稳定预测新样本。表现形式:
奥卡姆剃刀:偏好更简单的假设(如决策树剪枝)。
特征偏好:某些算法更关注特定特征(如SVM偏好间隔最大的分类面)。
2. 数学原理
假设空间搜索约束:

3.2、NFL定理(No Free Lunch Theorem)
1. 核心内容
核心结论:
在所有可能问题分布均匀的假设下,任何算法的期望性能相同。
即:若算法A在问题集 F1 上优于B,则必存在问题集 F2 使B优于A。脱离具体问题谈“最优算法”无意义,需匹配问题特性(如数据分布、目标函数)。
2. 数学原理
目标函数均匀分布假设:
设真实目标函数 f均匀分布在所有可能函数空间 F 中。期望误差推导:

证明核心:对所有 f 求和后,算法间的差异被抵消。
3.3、两者关联
偏好决定性能边界:
归纳偏好是算法“个性”,而NFL定理证明其性能高度依赖问题场景。
3.4、NFL定理应用实例
案例:西瓜分类中的算法选择
场景1:真实规律为“根蒂蜷缩→好瓜”
算法A:偏好“根蒂”特征(如决策树按信息增益优先选择根蒂)
→ 高准确率算法B:偏好“敲声”特征(如人为设定特征权重)
→ 低准确率
场景2:真实规律变为“敲声浊响→好瓜”
算法A:因错误偏好 → 准确率下降
算法B:与问题匹配 → 准确率上升
NFL生效:
若均匀随机出现两种场景,算法A和B的长期平均准确率相同。
实际项目应用建议:
问题分析优先:
考察数据分布(如特征相关性、噪声水平)
明确任务目标(如分类精度 vs. 模型解释性)
算法匹配策略:
问题特性 推荐算法 原因 特征间线性可分离 SVM/线性模型 偏好最大间隔/线性关系 高维非结构化数据 神经网络 偏好多层非线性特征提取 需可解释性 决策树 偏好规则简单性
3.5、关键问题解答
Q1: 算法A在部分问题优于B,在其他问题是否必然更差(仅个人不成熟的经验)
不一定。NFL定理仅保证在所有问题均匀分布时,A和B的平均性能相同。
实际中:若现实问题分布不均匀(如图像识别任务远多于语音任务),某些算法可能长期占优。
Q2: 如何将NFL定理应用于实际项目(仅个人不成熟的经验)
“万能算法”是幻想:
测试新问题时,至少比较3种不同偏好的算法(如树模型、神经网络、SVM)。问题拆解匹配偏好:
子任务1(特征选择):用偏好稀疏性的Lasso回归
子任务2(模式识别):用偏好复杂边界的神经网络
动态算法切换:
监控数据分布漂移(如用户行为变化),当原有算法性能下降时,切换至匹配新分布的算法。
4、一图小结
机器学习是 "数据→学习→模型→评估→优化" 的闭环系统,NFL定理要求我们根据问题特性动态调整算法偏好。
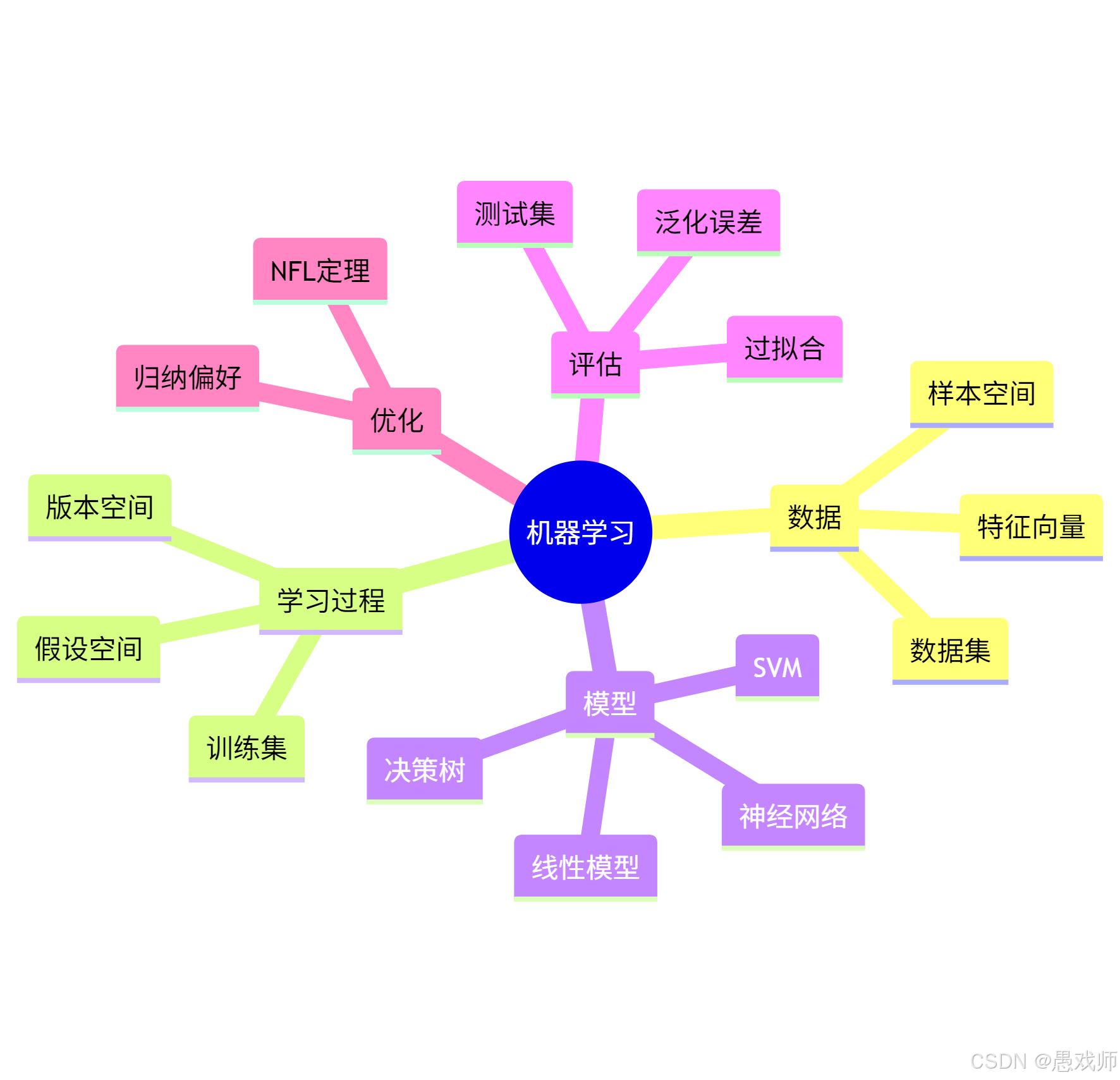
5、模型评估与选择
5.1、过拟合/欠拟合
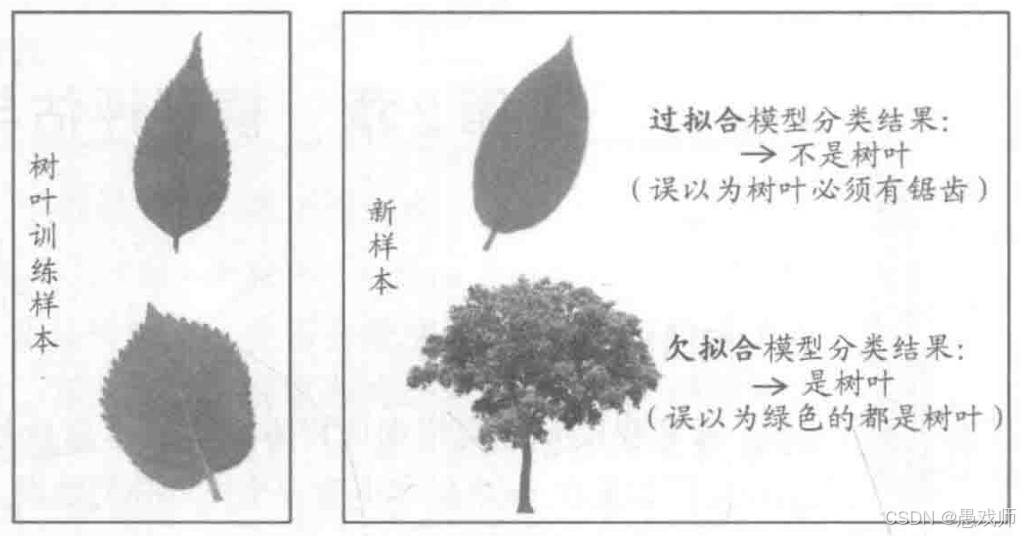 引用自西瓜书
引用自西瓜书
5.1.1、过拟合与欠拟合核心对比
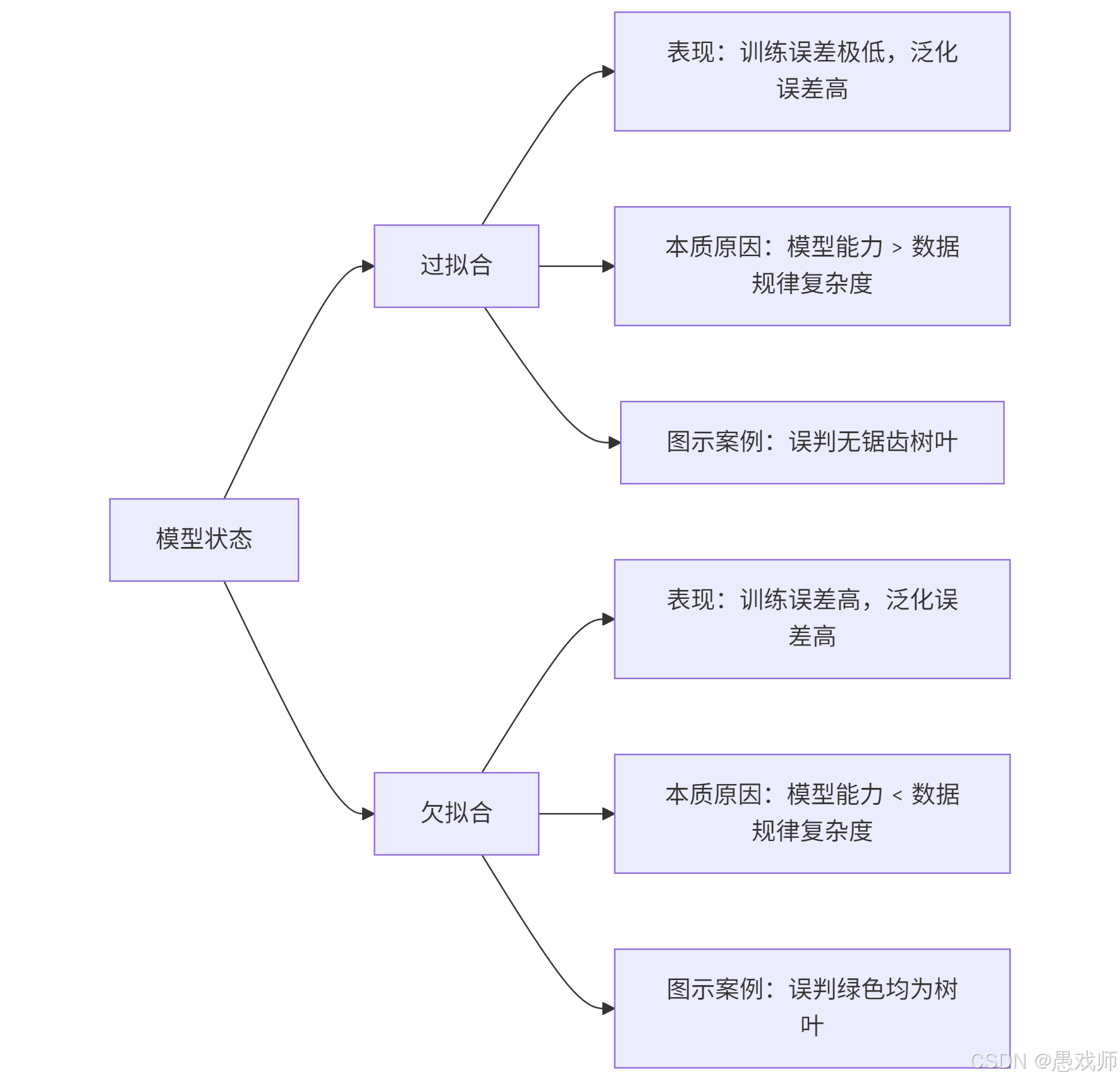 5.1.2、直观解析
5.1.2、直观解析
过拟合

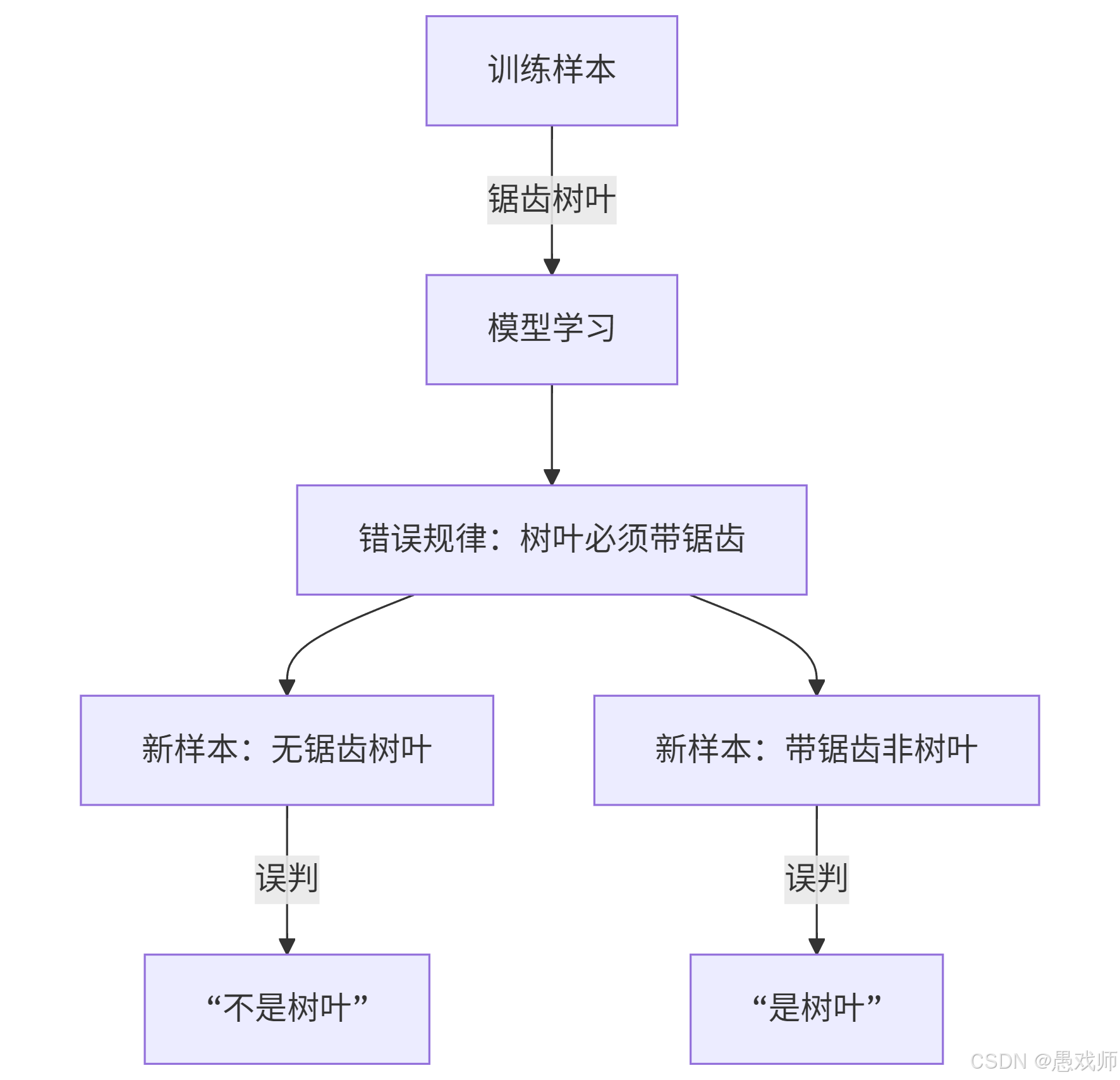
关键错误:将训练样本的偶然特性(锯齿)当作普遍规律
现实案例:人脸识别模型将"戴眼镜"作为必要特征,导致无法识别不戴眼镜的用户
欠拟合

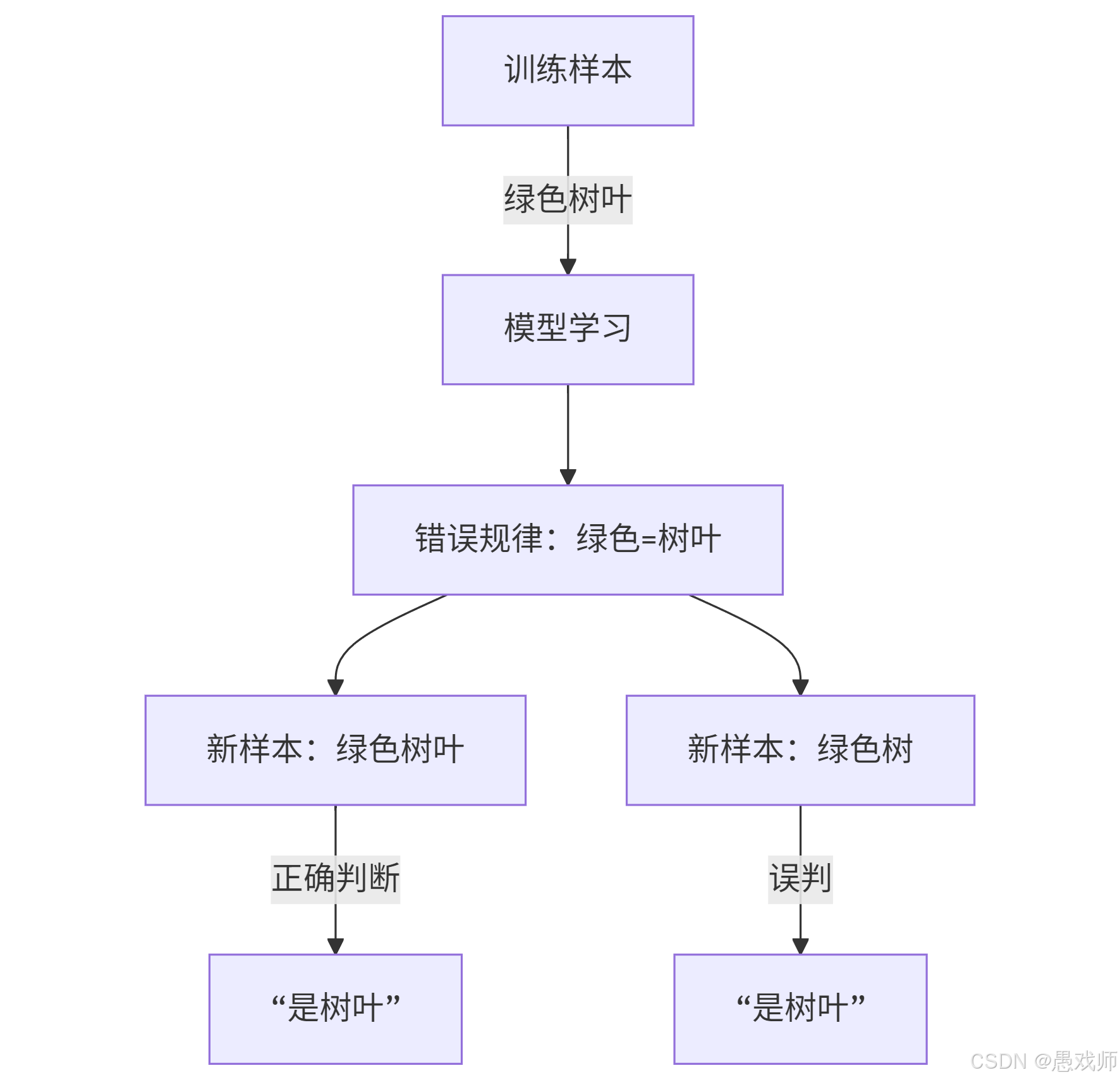
关键错误:未学习到形状、纹理等关键特征
现实案例:垃圾邮件过滤仅基于关键词"免费",误判重要邮件
对照表
| 维度 | 过拟合 | 欠拟合 |
|---|---|---|
| 模型能力 | 过于复杂(如深层神经网络) | 过于简单(如线性回归) |
| 数据匹配度 | 模型复杂度 > 真实规律复杂度 | 模型复杂度 < 真实规律复杂度 |
| 典型场景 | 小样本训练复杂模型 | 复杂问题用简单模型 |
| 解决方案 | 1. 增加训练数据量 2. 正则化(L1/L2) 3. 降低模型复杂度 4. Dropout(神经网络) | 1. 增加模型复杂度 2. 特征工程 3. 延长训练时间 4. 减少正则化强度 |
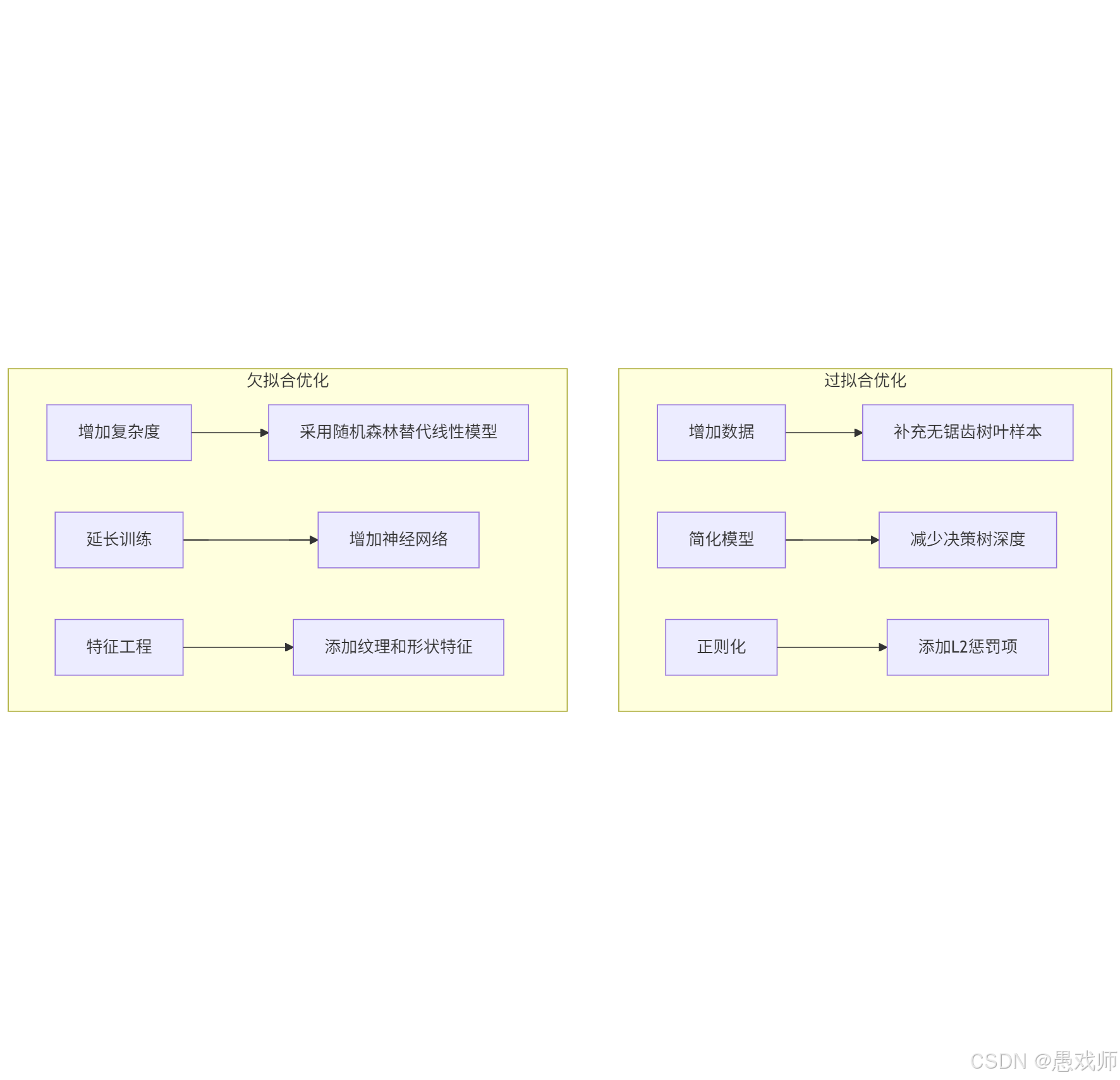
5.2、模型评估方法
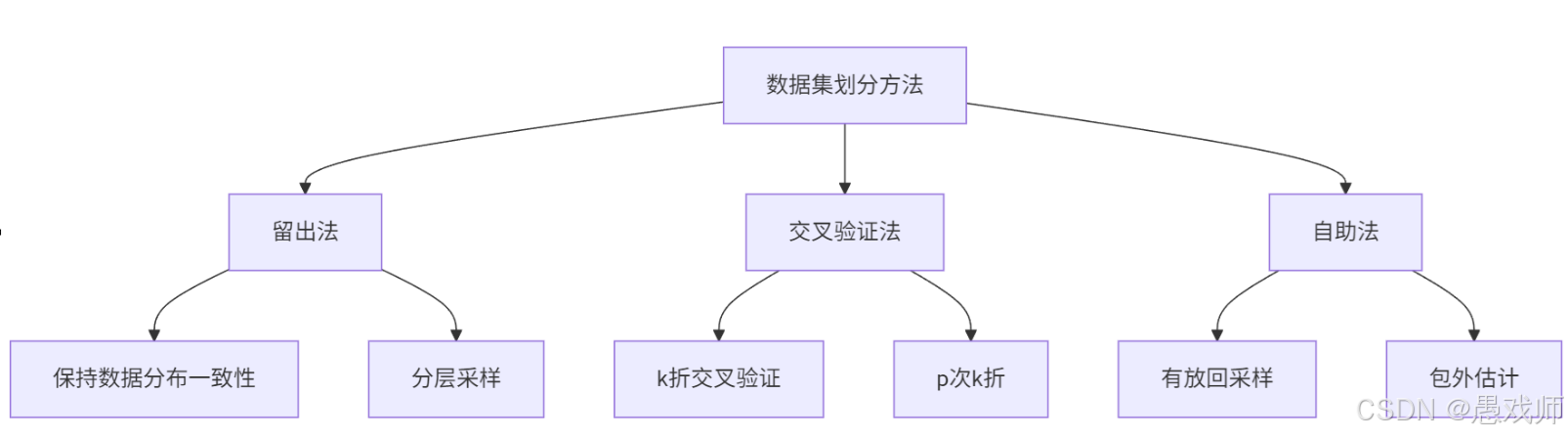
5.2.1、留出法(hold-out)
- 核心思想:将数据集 D 划分为两个互斥子集,分别作为训练集 S(用于训练模型)和测试集 T(用于评估性能),满足
。
- 关键要求:
- 划分需保持数据分布一致性(如分类任务采用 “分层采样” 保持类别比例),避免引入偏差。
- 单次划分结果不稳定,通常需多次随机划分并取平均值(如 100 次划分后的平均误差)。
- 常见比例:训练集占 2/3~4/5,测试集占 1/5~1/3。
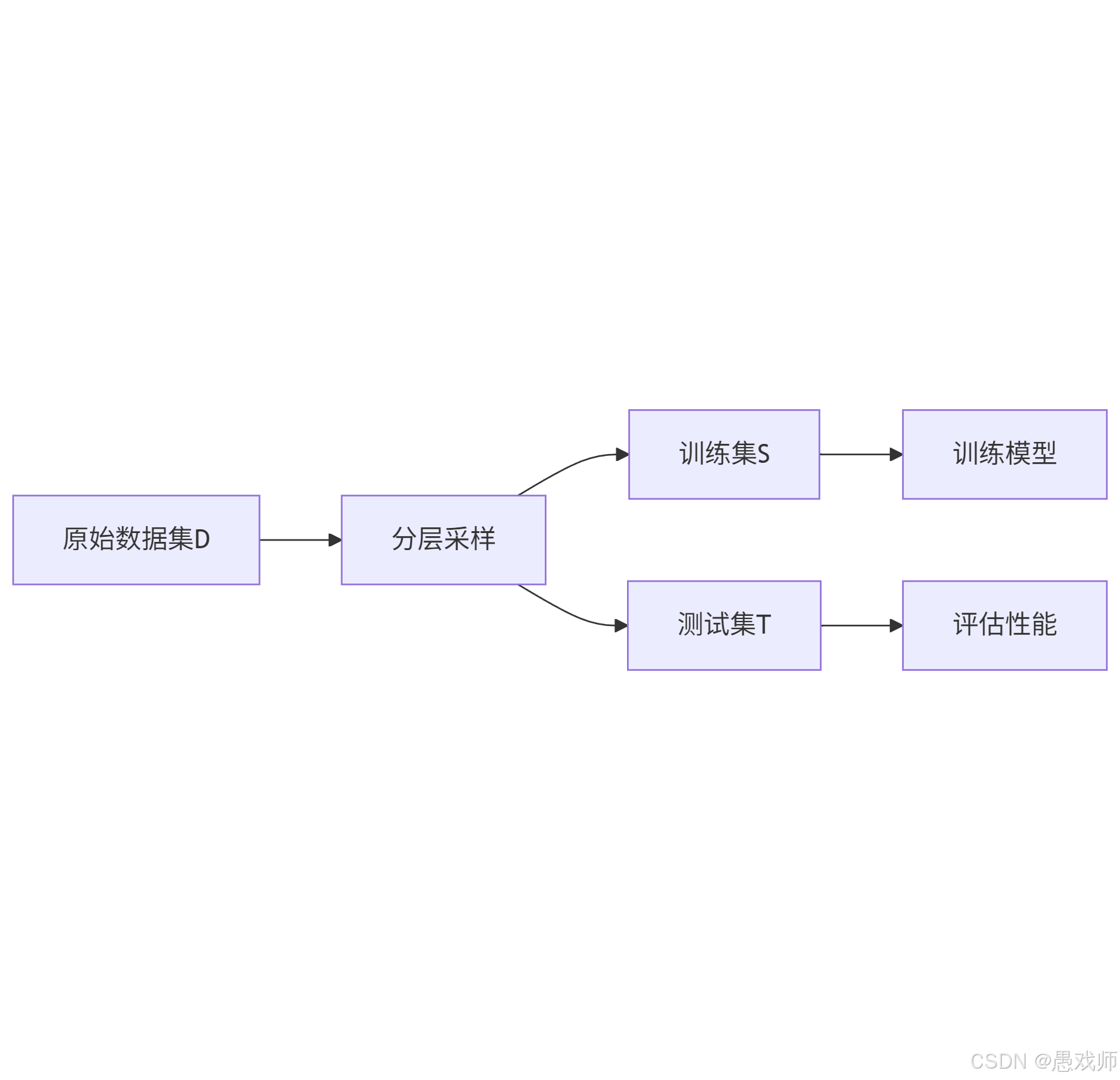
特点:
优点:简单高效,适合大数据集
缺点:单次划分结果波动大(需多次随机划分取平均)
关键要求:
分类任务必须分层采样(保持类别比例)
常用比例:训练集:测试集 = 7:3 或 8:2
5.2.2、 交叉验证法(Cross Validation)
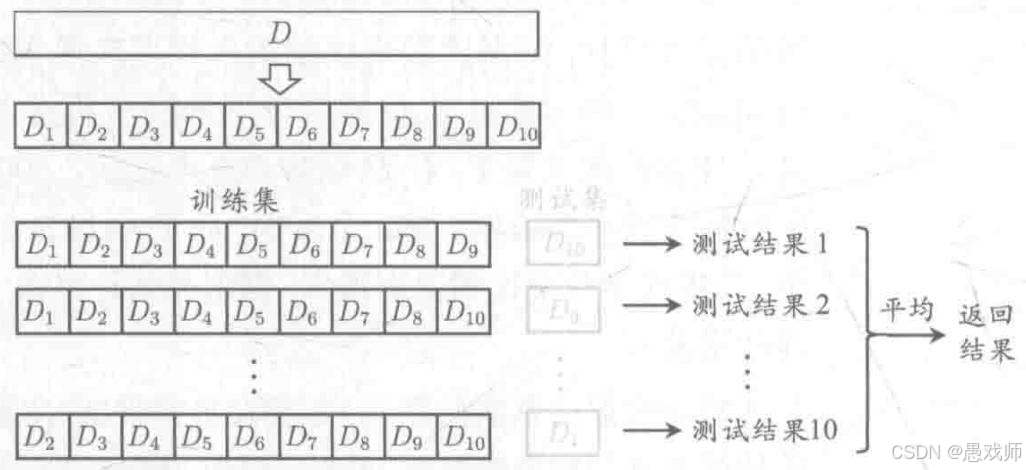 引用自西瓜书
引用自西瓜书
- 核心思想:将数据集 D 划分为 k 个大小相似的互斥子集(通过分层采样生成),每次用 k-1个子集的并集作为训练集,剩余 1 个子集作为测试集,重复 k 次后取平均误差,称为 “k折交叉验证”。
- 常用设置:
- k=10(最常用,称为 10 折交叉验证)。
- 为进一步提高稳定性,可采用 “p次k折交叉验证”(如 10 次 10 折交叉验证)。
- 特例:留一法(LOO):
- 当 k=m(m为样本数)时,每次留 1 个样本作为测试集,评估结果准确但计算开销极大(需训练m个模型)。
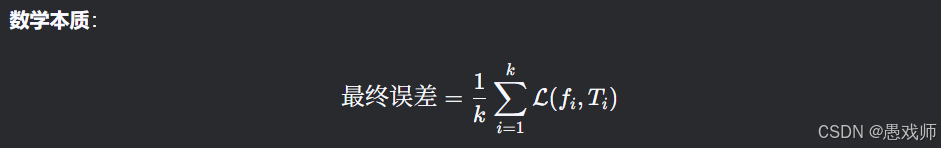
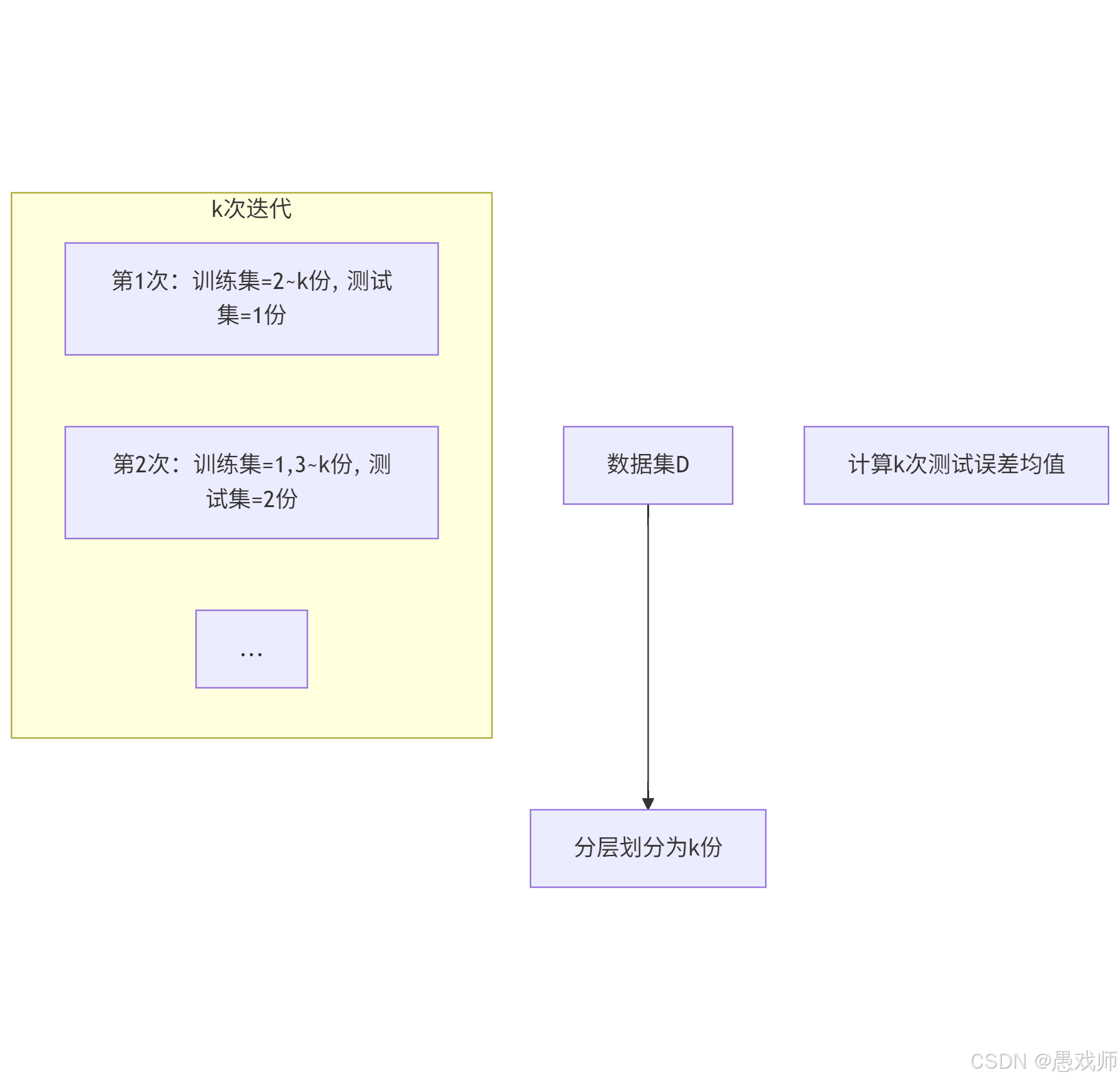
优势:
充分利用数据(每个样本都参与测试)
评估结果更稳定(尤其适合小数据集)
5.2.3、自助法(Bootstrapping)
我们希望评估的是用 D 训练出的模型,但在留出法和交叉验证法中,由于 保留了一部分样本用于测试,因此实际评估的模型所使用的训练集比 D 小,这 必然会引入一些因训练样本规模不同而导致的估计偏差,留一法受训练样本规 模变化的影响较小,但计算复杂度又太高了,有没有什么办法可以减少训练样 本规模不同造成的影响,同时还能比较高效地进行实验估计呢?
引用自西瓜书
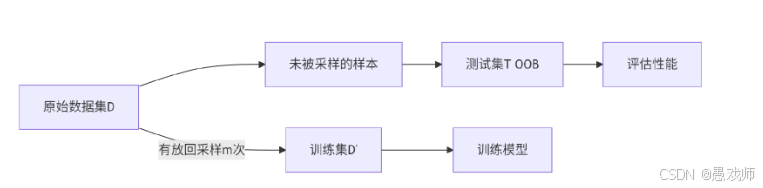
自助采样流程
初始化:空训练集 D′=∅
循环采样(重复 m次):
从 D 中随机选取一个样本 xi
将 xi的拷贝加入 D′
将 xi 放回 D 中
生成测试集:
T={x∈D∣x∉D′}(包外样本)
示例:
原始数据集 D={A,B,C},m=3 次采样:
第1次:抽到B → D′={B}
第2次:抽到B → D′={B,B}
第3次:抽到A → D′={B,B,A}
测试集 T={C}(未出现的样本)
数学证明 (字较丑,读友见谅)

方法特性分析
优势
| 特点 | 说明 | 应用价值 | ||
|---|---|---|---|---|
| 训练集规模 | (D'= m )(与原始数据集相同) | 小数据集也能充分训练模型 | ||
| 天然划分 | 自动生成包外测试集 | 无需人工划分数据 | ||
| 多重复用 | 可重复采样生成多个D′ | 集成学习(如Bagging)的基础 | ||
| 无分布假设 | 不依赖数据分布特性 | 适用于任意数据类型 |
局限
| 问题 | 数学解释 | 影响 |
|---|---|---|
| 分布偏差 | D′中样本独立同分布假设被破坏 | 模型估计可能有偏 |
| 样本相关性 | 重复样本导致训练集样本间独立性降低 | 方差估计不准确 |
| 包外样本偏差 | 包外样本非均匀覆盖(某些样本从未被测试) | 评估结果可能有噪点 |
6、性能度量指标
性能度量(performance measure)是衡量学习器泛化能力的评价标准,其选择需结合具体任务需求。
6.1、回归任务性能度量
回归任务的目标是预测连续值,核心是衡量预测值与真实值的差异,最常用指标为均方误差。
均方误差(Mean Squared Error, MSE)


实例分析:房价预测
样本集(单位:万元)
| 样本 | 真实房价 | 预测房价 | 误差 | 平方误差 |
|---|---|---|---|---|
| 1 | 300 | 280 | -20 | 400 |
| 2 | 450 | 460 | +10 | 100 |
| 3 | 500 | 520 | +20 | 400 |
| 4 | 380 | 350 | -30 | 900 |
| 5 | 600 | 620 | +20 | 400 |
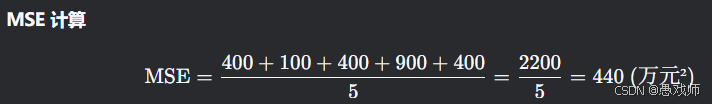
可读出的结论:
平均偏差:
虽然单样本误差有正有负,但平方消除方向影响,反映绝对偏差异常值敏感:
样本4的误差(-30)平方后达900,显著拉高MSE, 说明模型对低价房预测较差业务转换:
均方根误差(RMSE):440≈21 → 平均预测偏差21万元
相对误差:21/300=7%(低价房),21/600=3.5%(高价房)

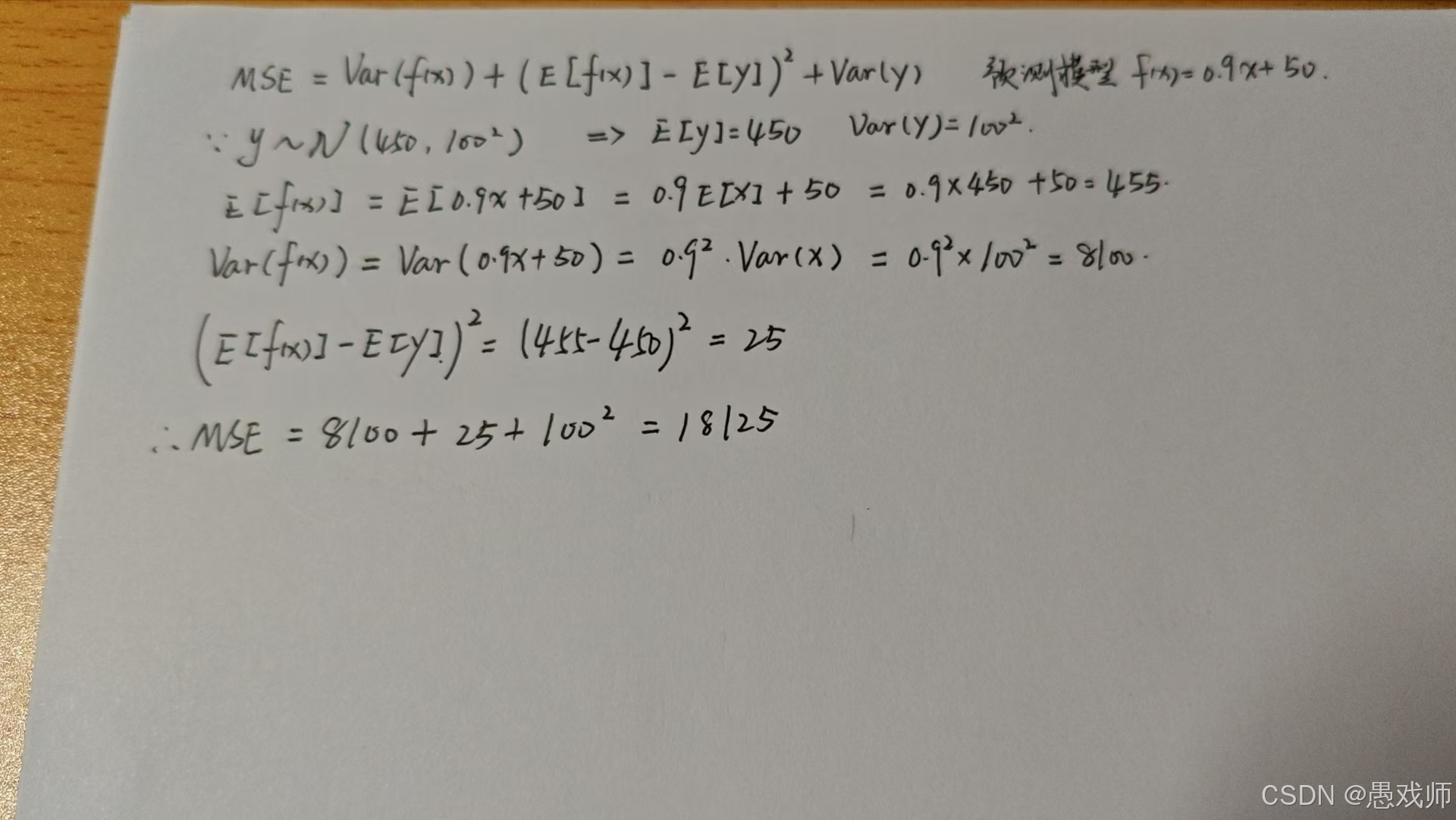
结论:
1. 模型方差(8,100 ≈ 44.7%)
来源:模型对输入 x 的波动过于敏感
数学表现:Var(f(x))=0.81×Var(x)
2. 偏差平方(25 ≈ 0.14%)
来源:模型系统性地高估房价 5 万元
数学表现:E[f(x)]−E[y]=5
3. 数据噪声(10,000 ≈ 55.2%)
来源:房价本身受市场、地段等不可控因素影响
数学表现:Var(y)=10,000
关键认知:
"这是无法通过模型优化的固有误差,代表预测精度的理论极限"
分解证明:


6.2、分类任务常用性能度量
分类任务的目标是预测离散类别,需根据任务关注的重点(如 “预测的准确率”“是否漏检” 等)选择指标,核心指标包括错误率、精度、查准率 - 查全率 - F1、ROC-AUC 等。
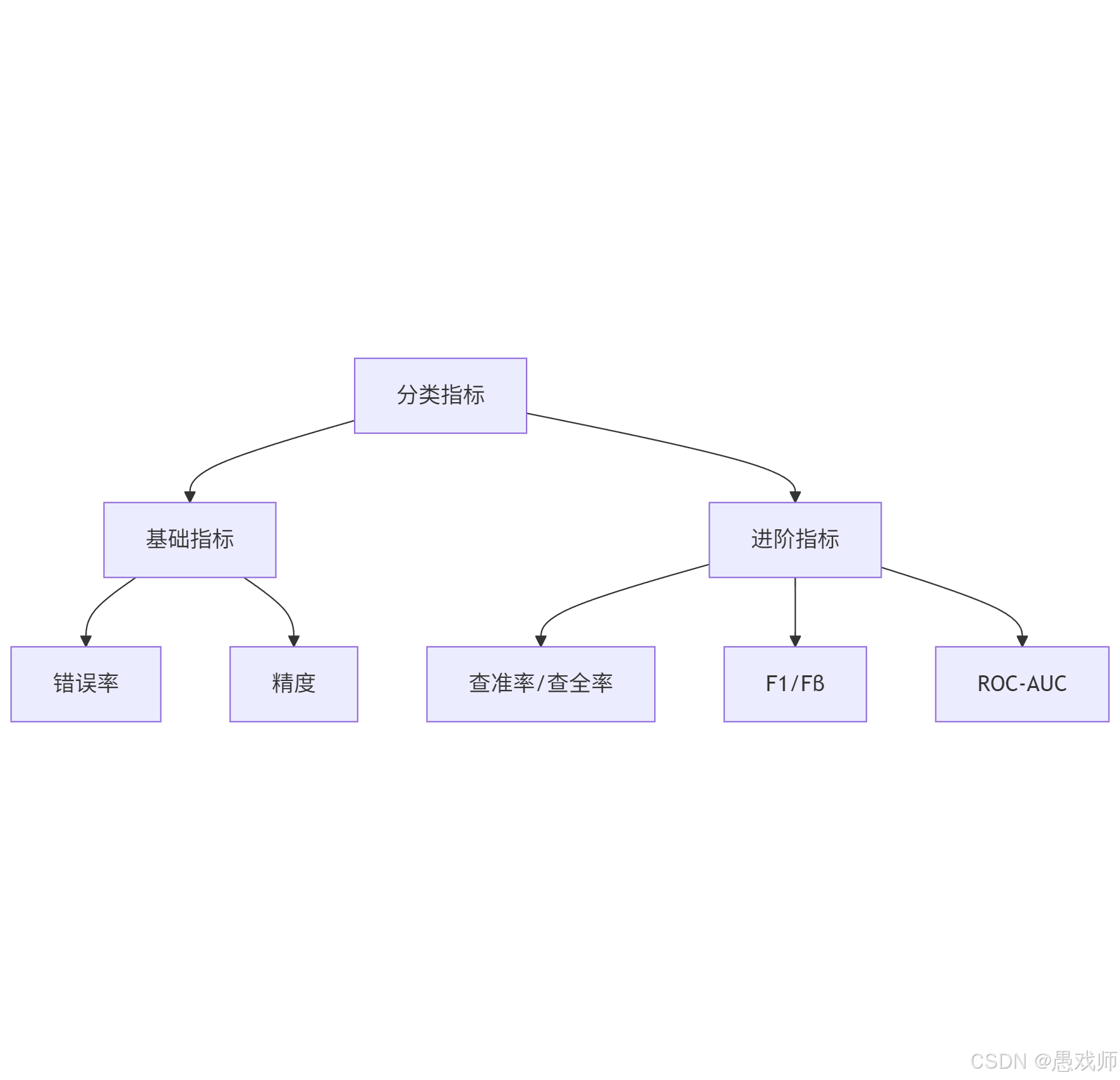
错误率与精度
1. 错误率(Error Rate)
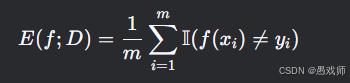
本质:错分样本占比
示例:
100个样本中错分15个 → 错误率=15%
2. 精度(Accuracy)
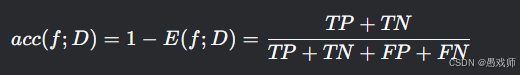
本质:正确分类样本占比
查准率(P)、查全率(R)与F1
混淆矩阵基础
预测正例 | 预测反例 | |
|---|---|---|
真实正例 | TP | FN |
真实反例 | FP | TN |
查准率(Precision)

意义:预测正例的可靠程度
例:推荐系统预测"用户会点击"的准确率
查全率(Recall)
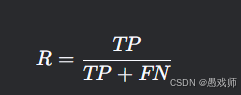
业务意义:正例样本的覆盖程度
例:疾病筛查中真正患者的检出率优化场景:
逃犯检索(避免漏检)
缺陷产品召回(减少漏召回)
F1 与 Fβ 分数(Precision、Recall)
指标 | 公式 | 特点 |
|---|---|---|
F1 | 平衡P与R(调和平均) | |
Fβ | 按需加权(β控制偏好) |
β的作用:
β > 1:更重查全率(如癌症筛查设β=2)
β < 1:更重查准率(如推荐系统设β=0.5)
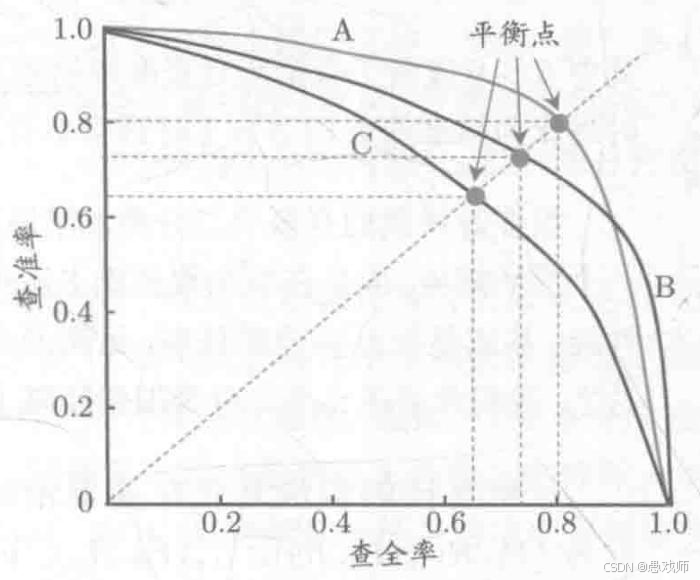 引用自西瓜书
引用自西瓜书
数学角度分析:
β值选择决策矩阵

实例解析:电商评论情感分析
场景设定
任务:判断评论是否负面(正例=负面评论)
混淆矩阵:
预测负面 预测非负面 真实负面 80 (TP) 20 (FN) 真实非负面 30 (FP) 870 (TN)
指标计算
查准率:
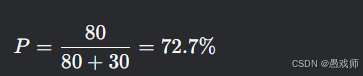
意义:预测为负面的评论中有72.7%真为负面
查全率:
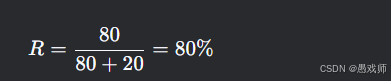
意义:所有负面评论中80%被正确识别
F1分数:
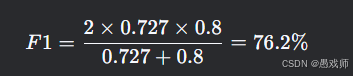
ROC-AUC
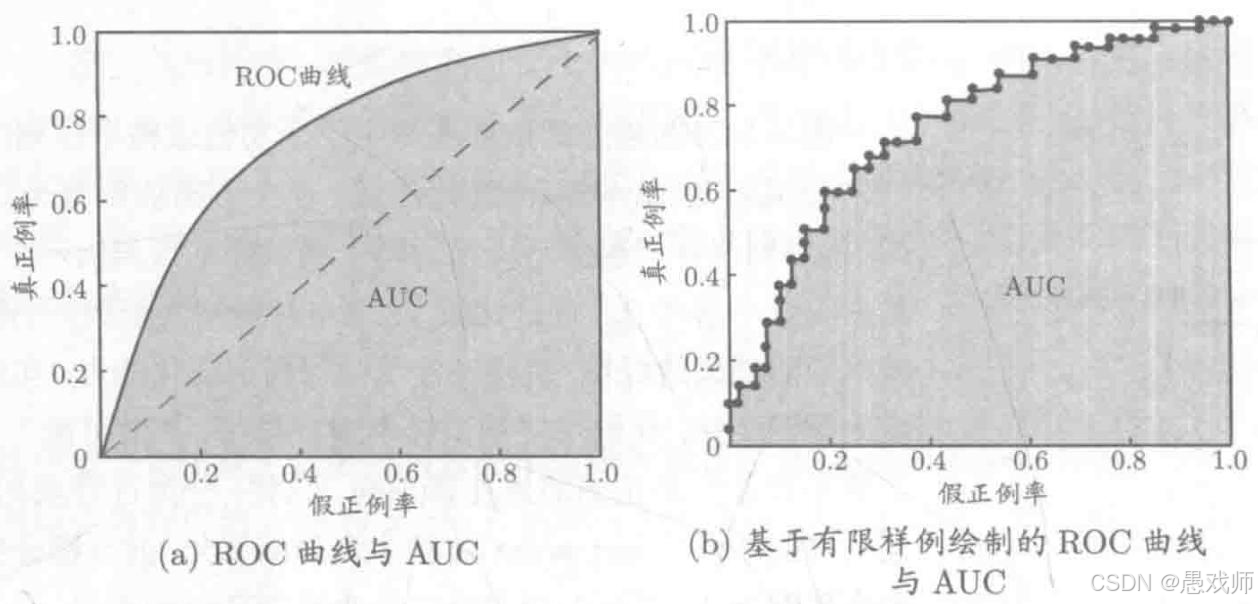
引用自西瓜书
ROC曲线核心:
横轴 (FPR - False Positive Rate):
FPR = FP / (FP + TN) = FP / N。代价: 误把负例判为正例的比例。我们希望它越低越好。纵轴 (TPR - True Positive Rate / Recall / Sensitivity):
TPR = TP / (TP + FN) = TP / P。收益: 正确识别出正例的比例。我们希望它越高越好。本质: ROC曲线描绘了当分类器的判别阈值(threshold) 从最严格(所有样本判负,TPR=0, FPR=0)到最宽松(所有样本判正,TPR=1, FPR=1)连续变化时,模型在“收益(TPR)”和“代价(FPR)”之间做出的权衡(Trade-off),即为了获得更高的正类识别率 (TPR),愿意承受多少负类的误报率 (FPR)。
理想点 (0,1): FPR=0(没有误判负例),TPR=1(所有正例都被正确识别)。完美分类器。
AUC核心:
- 定义: ROC曲线下的面积,取值范围[0, 1]。
- 物理意义 (最重要!): 随机选取一个正样本和一个负样本,分类器给正样本的打分高于给负样本打分的概率。即
AUC = P(Score₊ > Score₋)。
解读:
AUC = 0.5:模型没有区分能力(等价于随机猜测)。AUC > 0.5:模型具有一定的区分能力。值越接近1,区分能力越强。AUC < 0.5:模型性能比随机猜测还差(通常意味着模型预测反了,将正负类标签互换即可得到AUC > 0.5的模型)。- 优点: AUC值是一个单一标量,综合评估了模型在不同阈值下的整体性能,非常适合用于模型排序(哪个模型更好)。
计算 AUC (Area Under the ROC Curve) 主要有两种常用方法,它们本质上是等价的,但在实现上各有侧重
方法一:基于物理意义/排序法 (更常用、更高效)
这种方法直接利用 AUC 的物理意义:随机取一个正样本和一个负样本,分类器给正样本的打分高于负样本打分的概率。其计算步骤如下:
排序样本:
将所有样本(包括正样本和负样本)按照模型输出的预测得分/概率进行从高到低排序(最可能为正的排在最前面)。
如果多个样本的预测得分相同,需要特殊处理(见第2步)。
计算秩 (Rank):
给排序后的每个样本分配一个秩 (Rank)。
规则:
得分最高的样本秩为
n(总样本数n = P + N)。得分最低的样本秩为
1。关键:对于预测得分相同的样本,它们的秩取这些样本位置序号的
平均值。例如,排序后第 3, 4, 5 位的样本得分相同,那么它们的秩都是
(3 + 4 + 5) / 3 = 4。
计算正样本的秩和:
将所有正样本 (P个) 的秩加起来,得到
SumRank₊。
应用公式计算 AUC:
使用以下公式:
AUC = (SumRank₊ - P*(P+1)/2) / (P * N)
公式推导理解:
核心目标:计算正样本得分 > 负样本得分的概率
AUC 的物理意义是:随机取一个正样本和一个负样本,正样本预测得分高于负样本的概率。
等价于计算:
满足正样本得分 > 负样本得分的 (正, 负) 样本对数量 ÷ 所有可能的 (正, 负) 样本对总数
其中:所有可能的 (正, 负) 样本对总数 =
P * N关键思路:利用排序后的秩(Rank)
对所有样本按得分从高到低排序(得分最高排最前面)
给每个样本分配一个秩(Rank):
排名第1的样本 → Rank =
n(总样本数n = P + N)排名第2的样本 → Rank =
n-1...
排名最后的样本 → Rank =
1注:得分相同时,取平均秩(后面解释)
计算所有正样本的秩之和 →
SumRank₊为什么秩(Rank)能帮我们计算比较结果?
一个样本的
Rank值本质表示:有多少个样本排在它后面(得分比它低)。
因为:
最高分样本:后面有
n-1个样本 → Rank =n最低分样本:后面有
0个样本 → Rank =1对于任意一个正样本,它的
Rank值可拆解为:
Rank₊ = 排在其后的负样本数 + 排在其后的正样本数 + 1
(+1 是因为秩从1开始计数)推导第1步:展开所有正样本的秩和
把所有正样本的 Rank 加起来:
SumRank₊ = Σ(每个正样本的Rank) = Σ[ (排在其后的负样本数) + (排在其后的正样本数) + 1 ]拆解成三部分:
=Σ(排在其后的负样本数)+Σ(排在其后的正样本数)+Σ(1)其中:
Σ(1)= 正样本总数 =P
Σ(排在其后的正样本数)= 正样本之间的比较次数
(即每个正样本后面还有几个其他正样本)推导第2步:理解
Σ(排在其后的正样本数)想象所有正样本的排序:
最靠前的正样本:后面有
(P-1)个正样本第二靠前的正样本:后面有
(P-2)个正样本...
倒数第二的正样本:后面有
1个正样本最后的正样本:后面有
0个正样本所以:
Σ(排在其后的正样本数) = 0 + 1 + 2 + ... + (P-1) = P(P-1)/2
(等差数列求和公式)推导第3步:代回秩和公式
将上面结果代回:
SumRank₊ = Σ(排在其后的负样本数) + P(P-1)/2 + P
化简:
=Σ(排在其后的负样本数) + P(P+1)/2因此移项得:
Σ(排在其后的负样本数) = SumRank₊ - P(P+1)/2核心洞见:
Σ(排在其后的负样本数)就是我们要的答案!
Σ(排在其后的负样本数)的实际意义:
遍历每个正样本,计算 有多少个负样本排在该正样本后面(即得分比该正样本低)。
这正是 所有满足正样本得分 > 负样本得分的 (正, 负) 对的数量!最终得到AUC公式
满足条件的正负对数 =
SumRank₊ - P(P+1)/2
总正负对数 =P * N所以:
AUC = [SumRank₊ - P(P+1)/2] / (P * N)得分相同的情况如何处理?
当多个样本得分相同时:
它们在排序中占据连续位置(比如位置 k, k+1, ..., k+m-1)
它们的秩取平均值:
(k + (k+1) + ... + (k+m-1)) / m为什么取平均秩?
物理意义:如果1个正样本和1个负样本得分相同,我们认为正样本 > 负样本的概率是 0.5(即平局折半)
平均秩的分配方式恰好保证了:
正样本Rank - 负样本Rank = 0.5
从而在公式中实现+0.5的计数效果
最终计算概率:
(满足条件的正负对数) / (总正负对数) = [SumRank₊ - P*(P+1)/2] / (P * N)
例子:
假设有 10 个样本:3 个正样本 (P=3),7 个负样本 (N=7)。模型预测得分排序后样本类型和计算的秩如下:
样本位置 (得分高->低) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
样本类型 | P | N | P | N | N | N | P | N | N | N |
秩 (Rank) | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
正样本的秩:位置1: 10, 位置3: 8, 位置7: 4
SumRank₊ = 10 + 8 + 4 = 22P*(P+1)/2 = 3*4/2 = 6P*N = 3*7 = 21AUC = (22 - 6) / 21 = 16 / 21 ≈ 0.7619
方法二:梯形积分法 (基于 ROC 曲线绘制)
这种方法在绘制出 ROC 曲线后,通过计算曲线下的面积来得到 AUC。步骤如下:
绘制 ROC 曲线:
按预测得分从高到低排序样本。
设定初始阈值最大:
(FPR, TPR) = (0, 0)。依次降低阈值(或依次将每个样本划为正例):
如果当前样本是 真正例 (TP):
TPR增加1/P,点在图上 垂直向上 移动1/P。如果当前样本是 假正例 (FP):
FPR增加1/N,点在图上 水平向右 移动1/N。关键:遇到预测得分相同的样本时,将它们一起处理:
计算这批得分相同的样本中真正的正例数 (
TP_batch) 和假正例数 (FP_batch)。TPR一次性增加TP_batch / P。FPR一次性增加FP_batch / N。在图上从上一个点
(FPR_prev, TPR_prev)移动到新点(FPR_prev + FP_batch/N, TPR_prev + TP_batch/P)。
最终到达
(1, 1)。
计算曲线下面积:
将 ROC 曲线看作由一系列连续的点
(x_i, y_i)连接而成(包括起点(0, 0)和终点(1, 1))。使用 梯形法则 (Trapezoidal Rule) 计算曲线下的面积:
AUC = Σᵢ [ (xᵢ₊₁ - xᵢ) * (yᵢ + yᵢ₊₁) / 2 ]这个公式计算的是相邻两点
(xᵢ, yᵢ)和(xᵢ₊₁, yᵢ₊₁)之间形成的梯形面积,然后将所有梯形面积求和。也可以写成:
AUC = (1/2) * Σᵢ [ (xᵢ₊₁ - xᵢ) * (yᵢ + yᵢ₊₁) ]
例子: (使用上例数据)
假设绘制 ROC 曲线得到以下关键点(按顺序):
(x, y) = (0, 0), (0, 1/3), (1/7, 1/3), (1/7, 2/3), (2/7, 2/3), (2/7, 1), (1, 1)
计算相邻点间梯形面积:
(0,0) -> (0, 1/3):(0-0)*(0 + 1/3)/2 + (1/3 - 0)*(0 + 0)/2?特殊处理:垂直移动,宽度为0,面积为0。(0, 1/3) -> (1/7, 1/3): 水平移动Δx = 1/7,y₁ = y₂ = 1/3。面积 =(1/7) * (1/3 + 1/3)/2 = (1/7) * (2/3)/2 = (1/7)*(1/3) = 1/21(1/7, 1/3) -> (1/7, 2/3): 垂直移动Δx=0, 面积为0。(1/7, 2/3) -> (2/7, 2/3): 水平移动Δx=1/7,y₁=y₂=2/3。面积 =(1/7) * (2/3 + 2/3)/2 = (1/7) * (4/3)/2 = (1/7)*(2/3) = 2/21(2/7, 2/3) -> (2/7, 1): 垂直移动Δx=0, 面积为0。(2/7, 1) -> (1, 1): 水平移动Δx=5/7,y₁=y₂=1。面积 =(5/7) * (1 + 1)/2 = (5/7)*1 = 5/7
总 AUC = 0 + 1/21 + 0 + 2/21 + 0 + 5/7 = (1/21 + 2/21) + 15/21 = 3/21 + 15/21 = 18/21 = 6/7 ≈ 0.8571`
注意:这个例子中的点序列和计算只是为了演示梯形法,结果与排序法例子的结果不同,因为样本类型和顺序是假设的。