当前位置：首页 > news >正文

【每日算法】专题九_链表

news 2025/7/23 7:16:39

1. 算法思路

链表算法的核心思路可归纳为以下几点：

指针操作是核心
所有操作围绕指针展开，需精准控制节点的 next 指向，避免链表断裂（如反转时保存 next 指针，合并时正确拼接）。
技巧性工具
- 哑节点：简化头节点修改场景（如合并、删除），统一操作逻辑。
- 双指针：快慢指针找中点 / 环，前后指针反转链表，间距指针定位倒数节点。
典型场景解法
- 反转：迭代修改指针方向（整体 / 部分 / 分组反转）。
- 合并：双指针比较拼接（两链表），分治 / 堆优化（K 链表）。
- 环问题：快慢指针检测环及入口。
- 重排：拆分为两部分，反转后半段再交替合并。
边界处理
重点关注空链表、单节点、尾节点等特殊情况，避免越界。

核心是 “拆解问题 + 指针控制”，结合技巧简化逻辑。

2.例题

2.1 两数相加

2. 两数相加 - 力扣（LeetCode）

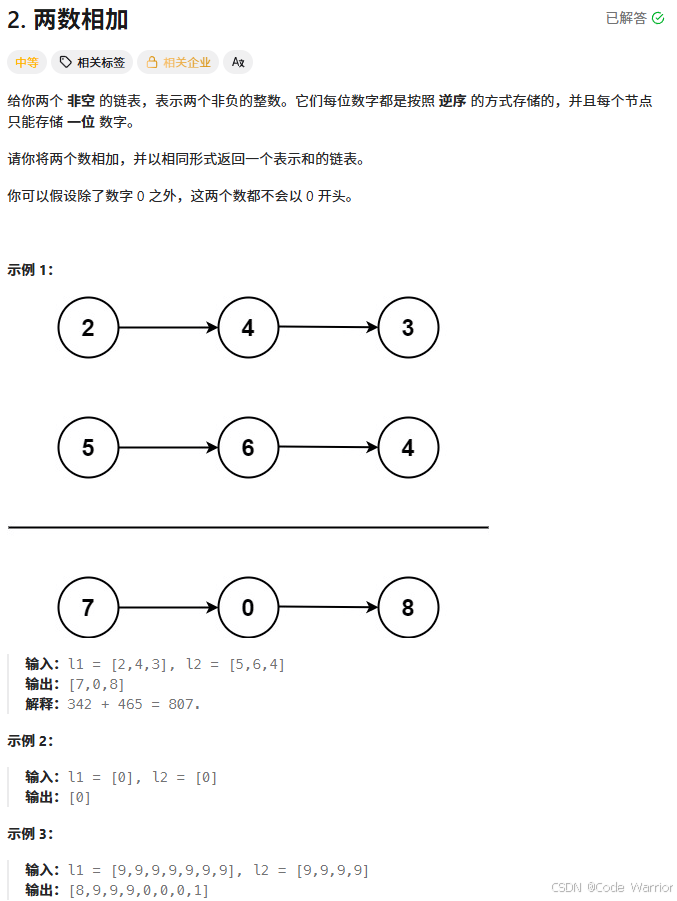
核心思想是模拟链表表示的两个大数相加的过程，通过逐位相加并处理进位，最终生成结果链表。

核心思路

模拟加法过程：
- 从两个链表的头节点开始，逐位相加对应节点的值，并加上前一位的进位（初始进位为 0）。
- 使用变量 t 存储当前位的和（包括进位），则当前位的值为 t % 10，新的进位为 t / 10。
处理链表长度不一致：
- 若两个链表长度不同，较短链表遍历完后，后续位的值视为 0。
- 循环条件为 cur1 || cur2 || t，确保所有位和最后一个进位都被处理。
结果链表构建：
- 使用哑节点 head 简化头节点的处理，避免分类讨论。
- 每次循环创建新节点存储当前位的值，并将其连接到结果链表的末尾。
内存管理：
- 手动释放哑节点 head 的内存，防止内存泄漏。

关键点

进位处理：变量 t 同时存储当前位的和与进位，简化逻辑。
边界条件：循环条件包含 t，确保最后一个进位被正确处理（如 999 + 1 = 1000）。
哑节点技巧：通过 head->next 获取真正的头节点，避免单独处理头节点的创建。

复杂度分析

时间复杂度：O (max (m, n))，其中 m 和 n 分别为两个链表的长度。
空间复杂度：O (max (m, n))，主要用于存储结果链表。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* cur1 = l1;ListNode* cur2 = l2;ListNode* head = new ListNode(0);ListNode* prev = head;int t = 0;while(cur1 || cur2 || t){if(cur1){t += cur1->val;cur1 = cur1->next;}if(cur2){t += cur2->val;cur2 = cur2->next;}prev->next = new ListNode(t % 10);prev = prev->next;t /= 10;}ListNode* ret = head->next;delete head;return ret;}
};

2.2 两两交换链表中的节点

24. 两两交换链表中的节点 - 力扣（LeetCode）

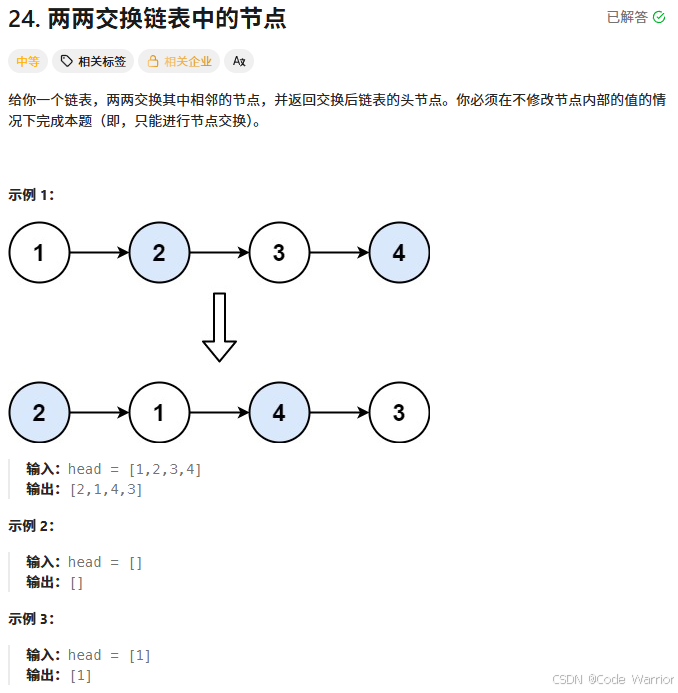
核心思想是通过迭代方式两两交换链表中的节点，利用哑节点简化边界处理，并通过指针操作实现节点交换。

核心思路

哑节点（Dummy Node）的使用：
- 创建哑节点 newhead，使其 next 指向原头节点 head，用于处理头节点可能被交换的情况。
- 使用 front 指针跟踪当前处理的两个节点的前一个节点，初始指向 newhead。
节点交换逻辑：
- 每次循环处理相邻的两个节点 head 和 head->next：
  1. 保存第二个节点 prev = head->next。
  2. 修改指针：head->next 指向第三个节点（即 prev->next）。
  3. 修改指针：prev->next 指向 head，完成两节点的交换。
  4. 修改指针：front->next 指向交换后的新头节点 prev。
指针更新：
- 将 front 移动到已交换的第二个节点（即当前的 head）。
- 将 head 移动到下一组待交换的第一个节点（即 front->next）。
循环终止条件：
- 当 head 或 head->next 为空时停止，确保每次处理的两个节点都存在。

关键点

哑节点的作用：避免单独处理头节点交换的情况，统一所有交换操作的逻辑。
指针操作顺序：需先保存第二个节点的指针，再修改各节点的 next 指针，避免链表断裂。
边界条件：通过检查 head 和 head->next 是否存在确保循环安全。

复杂度分析

时间复杂度：O (n)，其中 n 为链表长度，需遍历每个节点一次。
空间复杂度：O (1)，仅需常数级额外空间。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {ListNode* newhead = new ListNode(0);newhead->next = head;ListNode* front = newhead;while(head && head->next){// 交换前后两个节点ListNode* prev = head->next; // 记录后节点head->next = head->next->next; // 前节点的下一个节点指向后节点的下一个节点prev->next = head; // 后节点的下一个节点指向前节点front->next = prev; // 前节点的前节点指向后节点// 更新前后两个节点head = prev->next->next; front = prev->next;}ListNode* ret = newhead->next;delete newhead;return ret;}
};

2.3 重排链表

143. 重排链表 - 力扣（LeetCode）

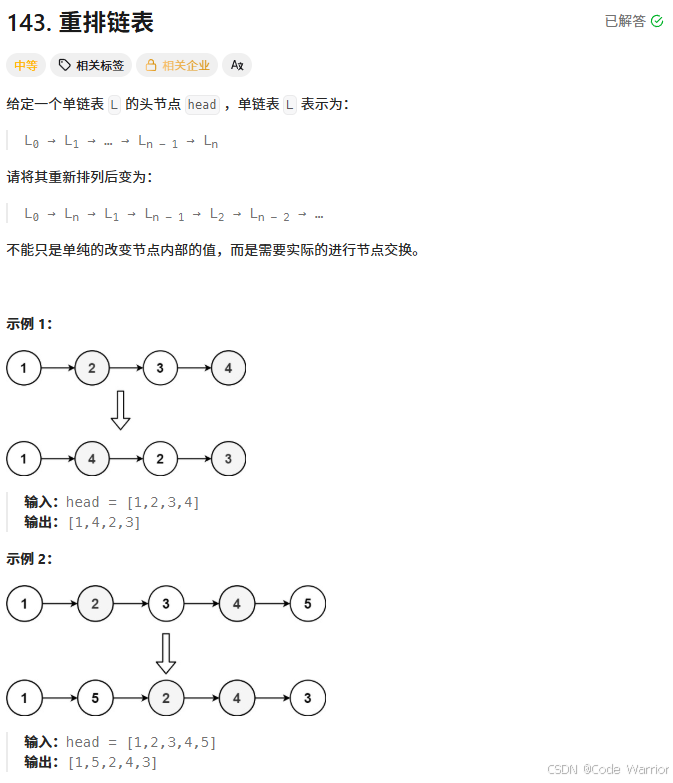
核心思想是将链表的后半部分反转后插入到前半部分中，实现链表的重排。具体分为三个步骤：

核心思路

找到链表中点：
- 使用快慢指针法：快指针 fast 每次移动两步，慢指针 slow 每次移动一步。
- 当 fast 到达末尾时，slow 恰好指向链表中点（对于偶数长度链表，中点为中间偏左的节点）。
- 断开前半部分和后半部分：slow->next = nullptr。
反转后半部分链表：
- 从中点的下一个节点开始，使用迭代法反转链表。
- 反转后，后半部分链表的方向被逆转，例如原链表 4->5->6 变为 6->5->4。
合并两个链表：
- 将前半部分和反转后的后半部分交替合并。
- 例如，前半部分 1->2->3 和后半部分 6->5->4 合并为 1->6->2->5->3->4。

关键点

快慢指针的应用：通过一次遍历找到链表中点，时间复杂度 O (n)。
链表反转的实现：通过迭代法原地反转链表，空间复杂度 O (1)。
交替合并的逻辑：使用临时指针保存后续节点，避免链表断裂。

复杂度分析

时间复杂度：O (n)，三个步骤均为线性时间。
空间复杂度：O (1)，仅需常数级额外空间。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:void reorderList(ListNode* head) {if (!head || !head->next) return;// 1. 找到中点ListNode* slow = head;ListNode* fast = head->next;while (fast && fast->next) {slow = slow->next;fast = fast->next->next;}ListNode* mid = slow->next;slow->next = nullptr; // 断开前半部分// 2. 反转后半部分ListNode* prev = nullptr;ListNode* curr = mid;while (curr) {ListNode* next = curr->next;curr->next = prev;prev = curr;curr = next;}// 3. 合并两个链表ListNode* first = head;ListNode* second = prev;while (second) {ListNode* temp1 = first->next;ListNode* temp2 = second->next;first->next = second;second->next = temp1;first = temp1;second = temp2;}}
};

2.4 合并 K 和升序链表

23. 合并 K 个升序链表 - 力扣（LeetCode）

核心思路是通过分治法递归合并多个有序链表，将k个链表的合并问题拆解为合并两个有序链表的子问题，最终得到整体有序的结果。

核心步骤

分治递归拆解：
- 将k个链表的合并任务递归分解：
  - 若链表范围为空（left > right），返回nullptr；若只有一个链表（left == right），直接返回该链表。
  - 否则，计算中间索引mid，将链表分为左半部分[left, mid]和右半部分[mid+1, right]，分别递归合并这两部分，得到两个合并后的有序链表l1和l2。
合并两个有序链表：
- 通过mergeTowlist函数实现两个有序链表的合并：
  - 创建哑节点head简化头节点处理，用指针prev构建结果链表。
  - 比较l1和l2当前节点的值，将较小的节点接入结果链表，并移动对应指针。
  - 当一个链表遍历完毕后，将另一个链表的剩余部分直接接入结果链表末尾。
递归回溯合并：
- 逐层递归合并子问题的结果，最终得到k个链表的总合并结果。

关键逻辑

分治思想：将k个链表的合并转化为logk次两个链表的合并，降低时间复杂度。
基础操作复用：核心依赖两个有序链表的合并逻辑，确保每次合并高效（线性时间）。
边界处理：通过递归基线条件（空链表或单个链表）避免无效操作，确保逻辑完整。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/class Solution {// struct compare// {//     bool operator()(const ListNode* l1, const ListNode* l2) const//     {//         return l1->val > l2->val;//     }// };public:ListNode* mergeKLists(vector<ListNode*>& lists) {// 优先级队列// priority_queue<ListNode*, vector<ListNode*>, compare> minHeap;// 小顶堆// for(auto l : lists)// {//     if(l) minHeap.push(l);// }// ListNode* newhead = new ListNode(0);// ListNode* prev = newhead;// while(!minHeap.empty())// {//     prev->next = minHeap.top();//     prev = prev->next;//     minHeap.pop();//     if(prev->next)//         minHeap.push(prev->next);// }// prev = newhead->next;// delete newhead;// return prev;// 归并return merge(lists, 0, lists.size() - 1);}ListNode* merge(vector<ListNode*>& lists, int left, int right){if(left > right) return nullptr;else if(left == right) return lists[left];int mid = (left + right) >> 1;// 处理左右区间ListNode* l1 = merge(lists, left, mid);ListNode* l2 = merge(lists, mid + 1, right);// 合并左右两个区间return mergeTowlist(l1, l2);}ListNode* mergeTowlist(ListNode* l1, ListNode* l2){if(l1 == nullptr) return l2;if(l2 == nullptr) return l1;ListNode head;ListNode* prev = &head, *cur1 = l1, *cur2 = l2;while(cur1 && cur2){if(cur1->val <= cur2->val){prev = prev->next = cur1;cur1 = cur1->next;}else{prev = prev->next = cur2;cur2 = cur2->next;}}if(cur1) prev->next = cur1;if(cur2) prev->next = cur2;return head.next;}
};

2.5 K 个一组翻转链表

25. K 个一组翻转链表 - 力扣（LeetCode）

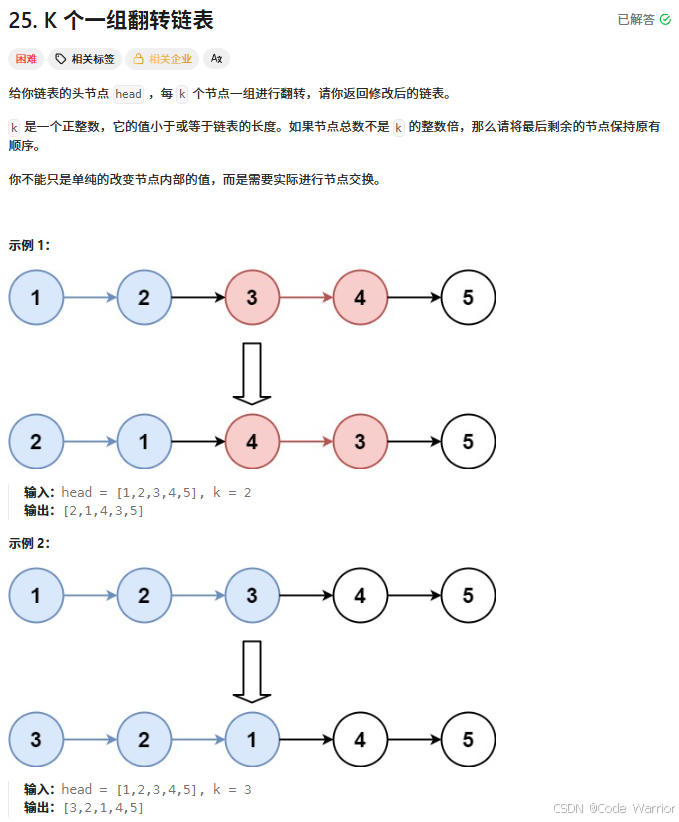
核心思路是按每 k 个节点为一组，迭代反转每组链表，对于不足 k 个节点的组则保持原样，最终拼接所有组得到结果。

核心步骤

分组标记与遍历：
- 使用指针 cur 遍历链表，通过计数器 t 记录当前组内的节点数量。
- 当 t 达到 k 时，说明当前组（从 head1 到 cur）包含 k 个节点，触发反转操作。
子链表反转处理：
- 标记当前组的尾节点 tail（即 cur），并断开该组与后续链表的连接（tail->next = nullptr），避免反转时影响其他节点。
- 以 head1 为起点，通过迭代法反转当前组：
  - 用 prev2 记录反转后的前驱节点，逐个将 head1 的 next 指向 prev2，完成节点反转。
  - 反转后，原尾节点变为新头节点，原头节点 head1 变为新尾节点。
组间拼接与指针更新：
- 将反转后的子链表通过 prev->next 接入结果链表（prev 为上一组的尾节点）。
- 更新 prev 为当前组的新尾节点（原 head1），作为下一组的前驱。
- 更新 head1 为下一组的起点（cur 已移动到下一组第一个节点），重置计数器 t。
剩余节点处理：
- 若遍历结束时，最后一组的节点数不足 k（t != 1），直接将剩余节点（从 head1 开始）接入结果链表，保持原有顺序。
哑节点辅助：
- 创建哑节点 newhead 简化头节点处理（避免头节点被反转导致的复杂逻辑），最终释放哑节点并返回有效头节点。

关键逻辑

分组反转的边界控制：通过计数器 t 精准控制每组节点数量，确保仅对 k 个节点的组执行反转。
链表断裂与拼接：反转前断开当前组与后续链表的连接，反转后重新拼接，保证每组操作独立。
剩余节点保留：对不足 k 个节点的组不反转，直接拼接，符合题目要求。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseKGroup(ListNode* head, int k) {int t = 1; // K 个一组的标记ListNode* newhead = new ListNode(0); ListNode* prev = newhead, *cur = head, // 遍历整个链表的节点*head1 = head;// 记录翻转区间的第一个节点while(cur){if(t == k) // 说明遍历到了 K 一组的子链表{ListNode *tail = cur; // 记录字链表的尾节点，使其next指向空cur = cur->next; // 更新curt = 1; // 更新标志位tail->next = nullptr; // next指向空ListNode* prev2 = nullptr; // 记录prev的next指向的上一个节点tail = head1;  // 更新翻转后的尾节点// 翻转子链表while(head1){// 记录head节点的next，使其能找到下一个节点ListNode* next = head1->next; prev->next = head1;head1->next = prev2;prev2 = head1;head1 = next;}prev = tail; // 更新prev到最后一个节点head1 = cur; // 更新到下一个子链表的头节点}if(cur) {cur = cur->next;++t;}}if(t != 1) prev->next = head1;prev = newhead->next;delete newhead;return prev;}
};

查看全文

http://www.xdnf.cn/news/1166797.html