周志华《机器学习导论》第13章 半监督学习
目录
1. 未标记样本
2. 生成式方法 高斯混合+EM
3. 半监督SVM 存在未标记样本的SVM变形
4. 图半监督学习 对图权值迭代矩阵计算
5. 基于分歧的方法 多视图协同训练
6. 半监督聚类 k-means的条件变形
6.1 Constrained k-means 利用“必连”与 “勿连”约束
6.2 Constrained Seed k-means 少量有标记的样本
在监督与无监督之间，少量标记样本的情况下，如何相比纯监督学习充分利用无标记样本的分布特征，相比无监督学习利用少量的已知信息？
对高斯混合分布、SVM、k-means进行一些修正和改进。
建模图论节点、边权迭代的思想；多视图协同训练、互相学习的思想。
1. 未标记样本
标记样本太少 用来训练不够； 还有很多未标记样本 全标记需要的成本太高
主动学习 active learning：每次挑对改善模型性能帮助大的样本 用少的专家查询 换取高性能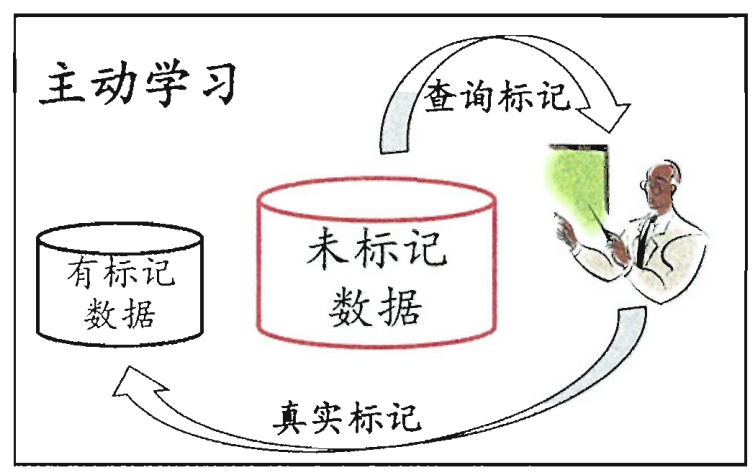
若不引用额外的专家知识可以吗？因为标记或未标记样本 都是由相同数据源 独立同分布采样
我们可以利用观察到的总样本分布：
聚类假设：假设数据存在簇结构，同一个簇的样本属于同一个类别
流形假设：假设数据 分布在一个流形结构上，邻近的样本拥有相似的输出值
比如这里 带判别样本是在标记正负中间 无法判断；
但把他们放在样本群里面 发现左边那一大块更有可能是+ 这个带判别也更有可能是正
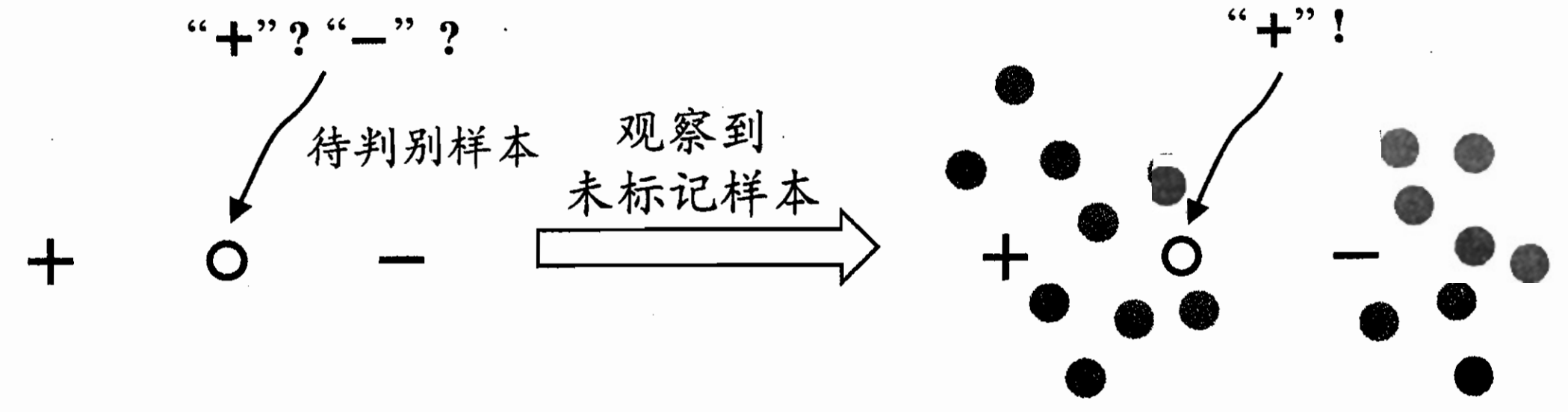
半监督学习：让学习器不依赖外界交互、 自动地利用未标记样本来提升学习性能
纯半监督学习：目标是预测样本外未观测到的数据
直推学习：目标是预测样本中 未标记数据
2. 生成式方法 高斯混合+EM
前置思想 周志华《机器学习导论》第9章 聚类中的高斯混合分布
样本由N个高斯分布加权组合而成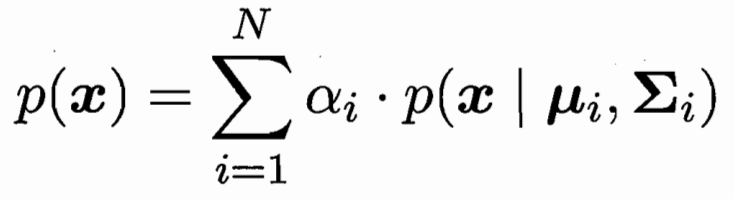
样本x属于第i个高斯分布的概率为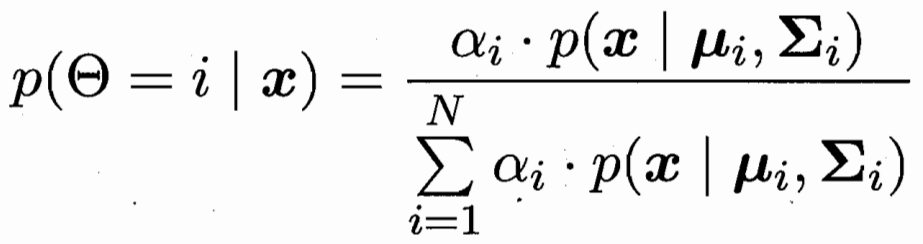
样本x对应后验概率最大的类别 j 条件概率 第i个高斯下的类别 j
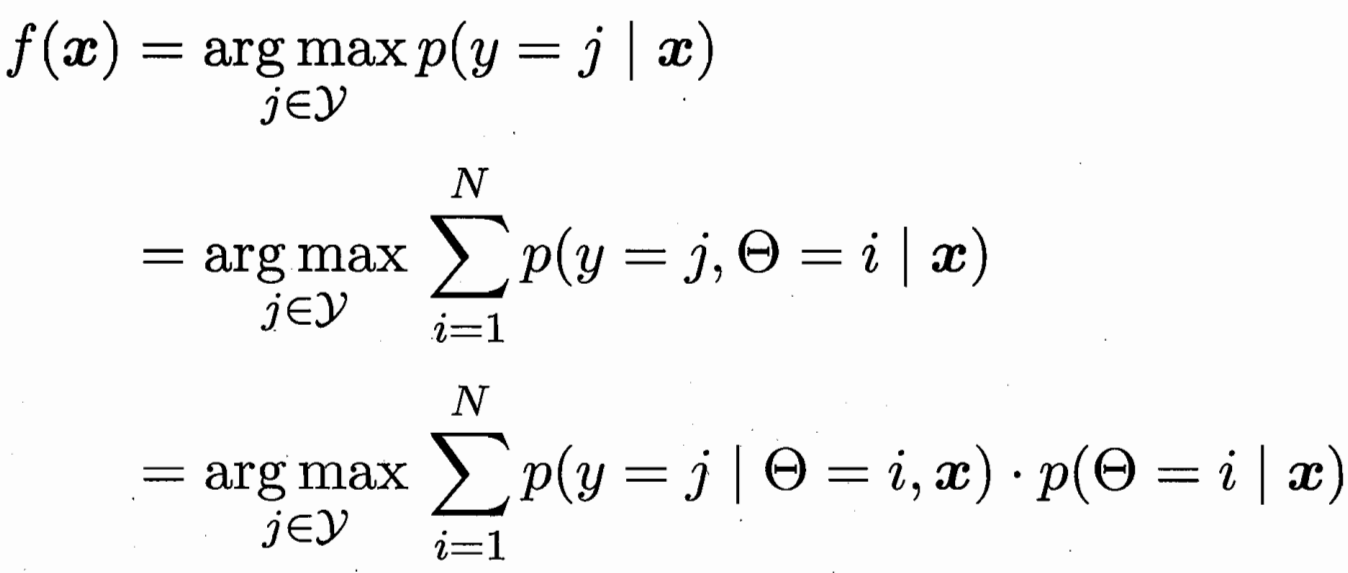
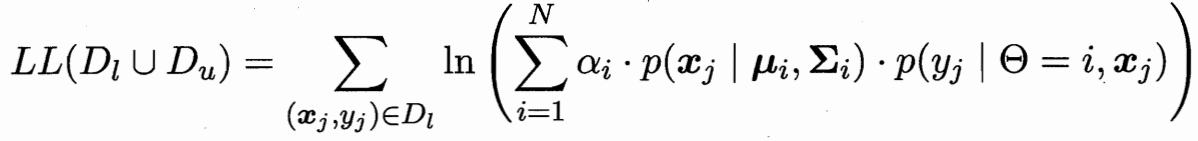
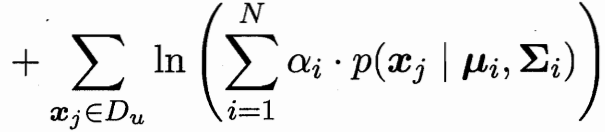极大似然估计 有标记的为(x,y)概率 无标记的为x概率
隐变量估计 EM算法 模型推隐变量-隐变量更新模型 重复至收敛
隐变量为 未标记样本 属于类别i高斯分布的概率
模型参数有：把未标记样本 依概率加权算作类i 更新类i的均值 方差 权重
3. 半监督SVM 存在未标记样本的SVM变形
TSVM 二分类：所有m个未标记样本（每个样本可能+ - 共2^m个可能里）
对于每一种可能 都SVM一下 选所有可能里间隔最大的那个划分超平面
周志华《机器学习导论》第5章 支持向量机SVM 前情回顾
这里的区别：之前有标记的 判别错误的惩罚项系数 比无标记的惩罚要高（前l有标记 后m无标记）
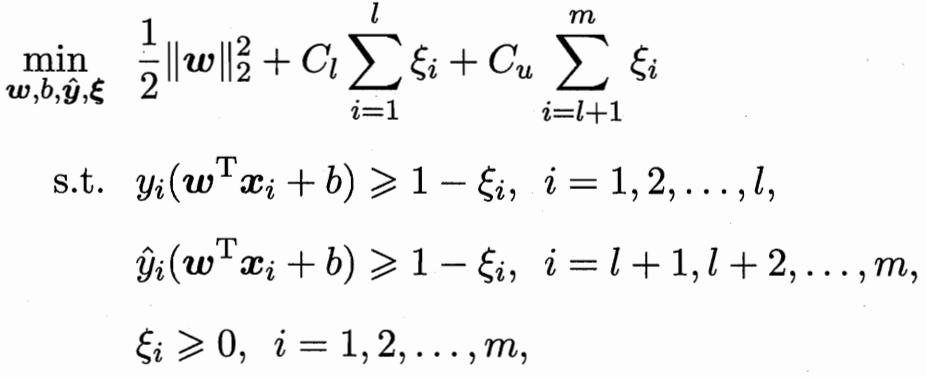
但这样2^m个超平面 计算复杂度还是太高了 考虑局部搜索迭代近似
先根据标记样本算出超平面 未标记样本根据超平面打上初始标记 Cu权重远小于Cl
1.把两个一正一负的 且出错可能性相对比较高（相加＞2）的标签 进行正负对调
2.把所有两两都检查一下后，重算SVM 并调高Cu权重。
一直重复1 2调整 直到Cu权重接近Cl。
为防止+ - 类别不平衡，进行调整权重操作 按照正负项数反比例
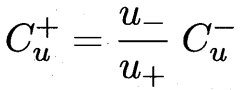
4. 图半监督学习 对图权值迭代矩阵计算
建模成图 每个样本为点 边值为两样本的相似度大小（可用高斯函数）
已标记样本为染色点 图半监督问题相当于扩展染色/传播 问题
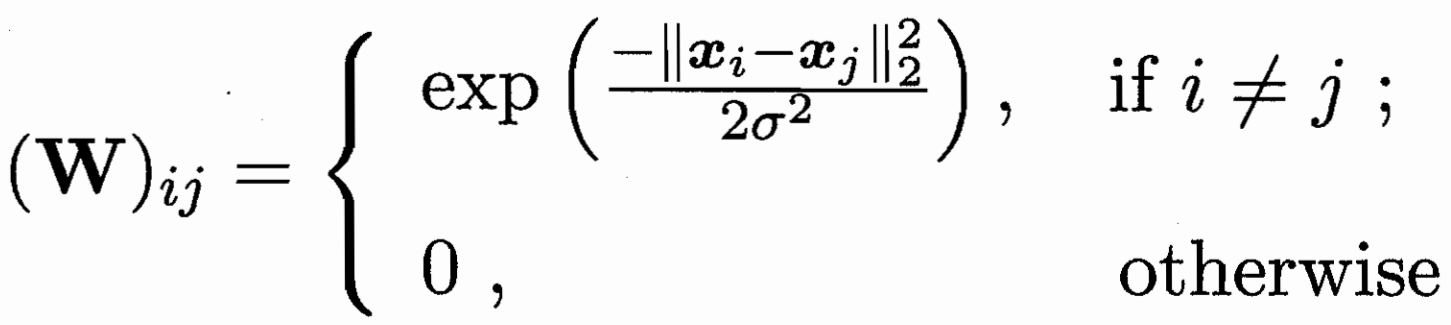
要学习一个函数f 可以把样本向量x 映射到一个值 把f前l和后u拆解 fl已知 需要优化 fu
目标函数为 最小化能量函数 W大的需要让他们的f接近
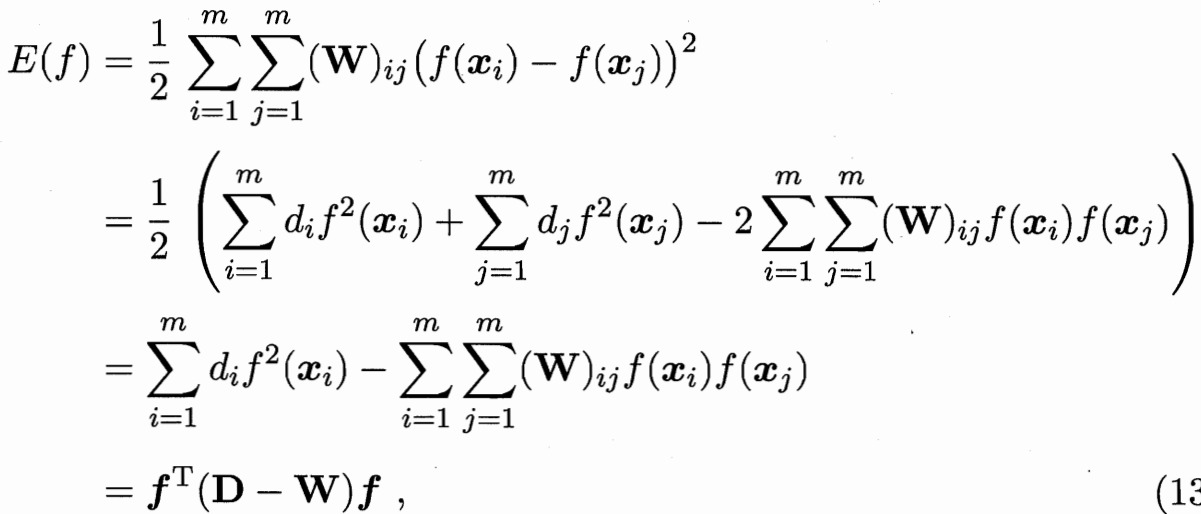
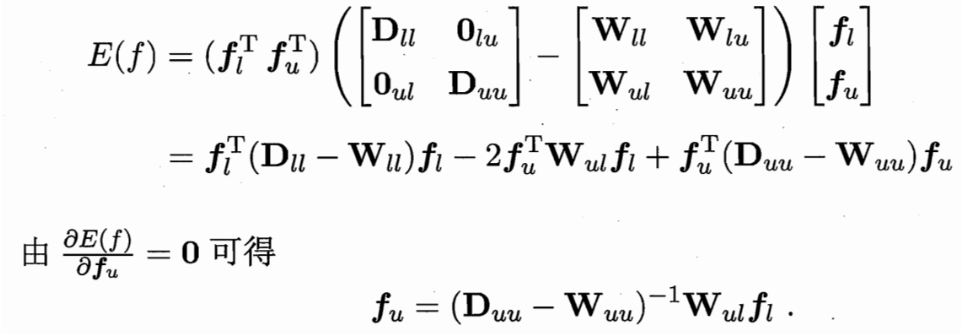
用一个 P=D逆W 可用Puu Pul 简化式子
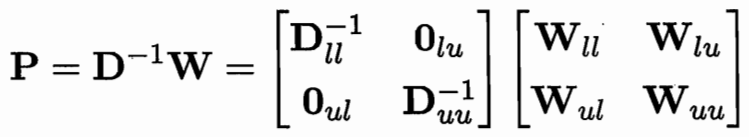
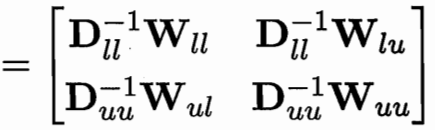
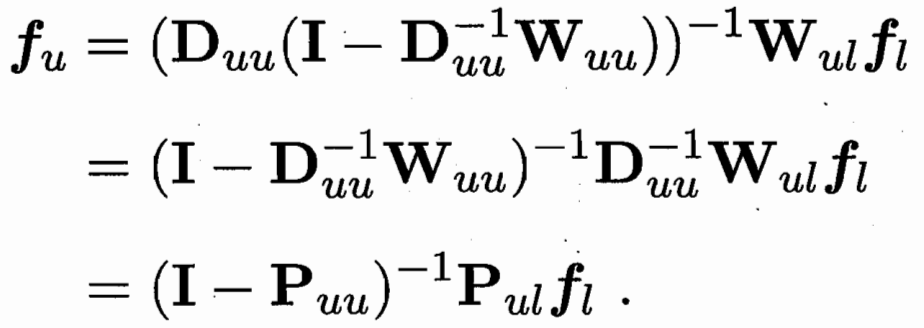
W可以推 D和P 求偏导得 fu和 fl的关系
如果是多分类的标记传播：f就不是映射到值 而是F 映射到一个向量；
每个样本 都会映射到一个长度为 |y| 的向量
最后的值为 向量最大数的位置（评估一下和每个类的相似度 分为相似度最大的那个）
初始的F是 前l样本对应的那类位置为1 矩阵其余位置均为0 一直迭代到F*收敛
S为W除以度数 归一化（防止高度数节点过度影响结果 保证特征值在[-1,1]内 使迭代过程收敛）
α的系数为迭代 (1-α)为保持初始Y的特征
令F(t+1)=F(t)
5. 基于分歧的方法 多视图协同训练
多视图数据：同一个数据对象不同方面的属性（如视觉、听觉上的）
协同训练：利用多视图的 相容性（判别答案的类别空间y相同）和互补性
假设数据拥有两个充分(每个视图都包含足以产生最优学习器的信息)且
条件独立（在给定类别标记条件下两个视图独立）视图：
每个视图的学习器，把自己最有把握的未标记样本打上标签给其他学习器学习（互相学习）
我知道你的信息 -> 我学到新东西告诉你 -> 你根据我的新信息 学到新东西告诉我
为防止所有样本都被大量改变：构建一个缓冲池 每次从缓冲池里找最有把握的
每次循环 对每个视图分别：1.根据已有数据训练分类器
2.在缓冲池里找 p个最有把握的正类和 n个最有把握的负类 打标记后 移除缓冲池
3.每个视图进行完毕后 补充缓冲池 从样本池随机抽一定样本移到缓冲池 维持每次循环前缓冲池中样本数目一定
6. 半监督聚类 k-means的条件变形
聚类本来无监督 但是有一些额外的信息的话 可以帮助聚类效果更好（带限制的k-means）
6.1 Constrained k-means 利用“必连”与 “勿连”约束
还是k个均值点μ 代表k个簇
每个样本依次塞到最近的 不违背“必连勿连约束”的簇； 分类好再取新的均值μ； 上两步迭代
6.2 Constrained Seed k-means 少量有标记的样本
用带标记的样本 初始化的k个μ；
并在后续的迭代过程中 不改变这些样本；无标记的样本类似传统k-means