Faithful Logical Reasoning via Symbolic Chain-of-Thought

投稿：ACL

代码链接： https://github.com/Aiden0526/SymbCoT

Abstract

虽然最近的思维链（Chain-of-Thought, CoT）技术通过theory of mind 增强了大型语言模型（large language models, llm）的推理能力，但它在处理大量依赖符号表达和严格的推理规则的逻辑推理方面可能仍然存在困难。为了加强llm的逻辑推理能力，我们提出了一种新的符号思维链（Symbolic Chain-of-Thought），即SymbCoT，这是一个完全基于llm的框架，将符号表达和逻辑规则与CoT提示相结合。从技术上讲，SymbCoT建立在LLM的基础上，

1) 首先将自然语言上下文翻译成符号格式，然后

2) 推导出一个循序渐进的计划，用符号逻辑规则来解决问题，

3) 接着是一个验证者来检查翻译和推理链。

通过对具有一阶逻辑和约束优化符号表达式的5个标准数据集的全面评估，SymbCoT在CoT方法的基础上不断显示出惊人的改进，同时刷新了当前最先进的性能。我们进一步证明了我们的系统在更忠实、灵活和可解释的逻辑推理方面取得了进步。据我们所知，这是第一次将符号表达式和规则结合到使用llm进行逻辑推理的CoT中。

分析一下这个图， 

Premises（前提）:
排行榜上有一个六人并列（six-way tie）。
其中有一人来自比利时。
Descampe 来自比利时，并出现在1992年 du Maurier Classic 的排行榜上。
结论待判断：
Descampe 是否在该六人并列的榜单中？

🔶 Chain-of-Thought（传统自然语言推理）
这部分通过日常语言的方式进行推理：因为有一个六人并列且其中一人来自比利时，而 Descampe 也来自比利时并在排行榜上，所以“Descampe 是在六人并列中的那个人”。
只是说有一个比利时人处于六人并列中，但不能因此就断定 Descampe 就是那个人。
所以这是一个逻辑错误❌，结论被错误地判定为“True”。问题：“overgeneralization（过度泛化）”

🟩 Symbolic Chain-of-Thought（符号化逻辑推理）
形式逻辑（First-Order Logic）推理的过程，更严格：∃x (Tie(x, sixWay) ∧ From(x, Belgium)) → 存在一位比利时人处于六人并列中。From(Descampe, Belgium) ∧ Leaderboard(Descampe, 1992DuMaurierClassic) → Descampe 来自比利时且在排行榜中。

因此，本文的主要贡献为：
•    proposing a fully LLM-based logical reason-ing framework based on CoT, demonstrating that LLMs can achieve robust logical reasoning capabilities without external reasoning tools. Compared to existing SoTA solutions relying on external resolvers, SymbCoT offers better robustness against translation errors and more human-understandable explanations.
•    innovatively integrating the strengths of symbolic forms and natural language expressions, enabling precise reasoning calculations while fully interpreting implicit information and cap-turing rich contexts.
•    introducing a plan-then-solve architecture for CoT reasoning, along with a retrospective veri-fication mechanism, enhancing the faithfulness of the reasoning process.

Related work

Chain of Thought

considering more intermediate steps and the rationales behind decision-making 

Subsequent tech-nologies have introduced more advanced reason-ing frameworks, incorporating mechanisms such as self-consistency and non-linear, multidimensional topological structures, e.g., Tree-of-Thought (Yao et al., 2023), Graph-of-Thought (Besta et al., 2023; Zheng et al., 2024), and other variants (Zhang et al., 2023b; Wang et al., 2023a).

Logical reasoning 

Previous works have explored rule-based (Robinson, 1965) and neural-based solving (Amayuelas et al., 2022; Gerasimova et al., 2023) methods for interpret-ing symbolic representations.

The latest trend in-volves integrating LLMs into the symbolic reasoning process (Ye et al., 2023; Gaur and Saunshi, 2023).

 For example, Logic-LM (Pan et al., 2023) and LINC (Olausson et al., 2023) consider using LLMs as translators to convert natural language into symbolic syntax such as FOL, which is then processed by external reasoning tools to enhance reasoning performance. 

FOL*
FOL 是一种用来精确表达对象之间关系和性质的逻辑系统，广泛应用于数学、人工智能、自动推理等领域。

组成部分：

1. 个体常量（Constants）：表示具体的对象，例如 John、a。

2. 变量（Variables）：用来泛指对象，例如 x、y。

3. 函数（Functions）：表示对象之间的映射关系，例如 fatherOf(x)。

4. 谓词（Predicates）：表示对象的属性或对象之间的关系，例如：

   • Human(x) 表示“x 是人”

   • Loves(John, Mary) 表示“John 爱 Mary”

5. 量词（Quantifiers）：

   • ∀x（全称量词）：对所有 x 都成立（e.g. ∀x Human(x) → Mortal(x)）

   • ∃x（存在量词）：存在某个 x（e.g. ∃x Cat(x) ∧ Black(x)）

6. 逻辑连接词：

   • ¬（not），∧（and），∨（or），→（if...then），↔（iff）

merely utilizing LLMs as transla-tors does not inherently enhance their logical rea-soning capabilities.

This work pioneers the devel-opment of the first symbolic CoT specifically de-signed for logical reasoning, fully utilizing LLMs.

question solution:

Problem	Solution
External reasoners require strict formatting, where any translation error by LLMs can lead to failure in parsing and reasoning.	Our reasoning steps, facilitated by the LLM, exhibit greater robustness against syntax errors.
The reasoning process may lack a human-friendly explanation throughout.	The entire reasoning process is conducted by the LLM, providing rationales that ensure a more human-friendly explanation throughout.
Difficulty in achieving precise reasoning calculations while interpreting implicit information inherent in natural language.	We propose a blend of symbolic forms and natural language expressions within the logical reasoning process, achieving precise reasoning calculations while fully interpreting implicit information inherent in natural language.
Ensuring the faithfulness of the reasoning process.	introduce a plan-then-solve CoT reasoning architecture and a verification mechanism

Method

Task Definition

The logical reasoning is defined as: formally, given a set of premises P = {p1, p2, . . . , pn}, where each pi represents a logical statement, we aim to derive a conclusion regarding a given statement S. The objective is to determine whether S is true (T ), false (F ), or unknown (U) based on the logical inferences drawn from the premises. 

Example:
<Premises> (P )
A hawk never lands. Some birds are hawks. <Statement> (S)
All birds land.
<Answer>
False.

Modules

As shown in Fig. 2, our SymbCoT system is fully supported by LLMs and comprises four distinct modules: Translator, Planner, Solver, and Verifier, whose roles are elaborated as follows. 

Translator
converts the premises and a question statement from natural language to a symbolic format. 

Planner
breaks down the raw problem into smaller sub-problems, which develop a detailed, step-by-step plan that connects the given premises to the question statement in both natural language and symbolic form. 

Solver
is tasked with deriving the answer through a sequential logical inference process given the premises and question statement, along with a meticulously crafted plan.  e.g LLM is explicitly instructed to apply logical deduction techniques adhering to FOL such as Modus Tollens (Enderton, 1972), e.g., If ¬B, and (A → B), then ¬A.

*Modus Tollens（拉丁语，意为“否定后件式”）是一个经典的逻辑推理规则，用于演绎推理，常见于形式逻辑和哲学论证中。

推理形式	结构	中文释义
Modus Ponens	P → Q，P，因此 Q	肯定前件式（正向）
Modus Tollens	P → Q，¬Q，因此 ¬P	否定后件式（反向）

Verifier
1) validates the correctness of symbolic translations by prompting the LLM to ascertain their semantic equivalence to the corresponding natural language. If discrepancies （差异） are identified, the lan-guage model refines the symbolic translation based on the original natural language to ensure semantic consistency.

2) Second, it verifies the output of the Solver containing step-by-step logical reasoning with the final answer. The Verifier scrutinizes检查 each logic deduction made, to ensure they strictly comply with the prin-ciples of formal logic. If invalid logic is found, the Verifier refines the reasoning steps according to the correct logic to arrive at a new answer.

Reasoning Steps

Step 1: Translating natural language context into symbolic.
对应translator组件

 Given the original set of premises P = {p1, p2, . . . , pn} and the question statement S

the Translator will first interpret them into the corresponding symbolic format, denoted as
P ′ = {p′1, p′2, . . . , p′n} and S′.

We concatenate the natural language and symbolic expression P and P ′ as Pc, S and S′ as Sc, i.e., hybrid format expressions for the future steps of reasoning.

Step 2: Deriving plan based on the natural and symbolic context.

对应planner组件

At this stage, the Planner module, utilizing Pc and Sc, constructs a plan comprising intermediate steps I = {i1, i2, . . . , im}. These steps form logical inferences sequentially bridging the premises Pc towards the question statement Sc. 

Step 3: Solving the problem given context and plan. 

对应solver组件

Here, the Solver operates on the premises Pc, the question statement Sc, and the plan I, by systematically applying logic rules. It iteratively selects pertinent premises and infers new insights through a sequence of reasoning steps  D = {d1, d2, . . . , dl}. Here, each dk signifies an insight inferred from the relevant premises dur-ing the iteration process, contributing to the elucidatio（说明） of Sc. This iterative methodology leads to a conclusive determination C, assigning the statement Sc as true (T ), false (F ), or uncertain (U).

Step 4: Verifying the translation and solving process.

对应Verifier 组件

Now based on the concatenated inputs Pc and Sc from Step 1, and the reasoning chain D and derived conclusion C from Step 3, the Verifier conducts two ways of verification process.

First, it checks whether the symbolic language is correctly translated based on the original natural lan-guage context, represented as Vtrans = Verify(P → P ′, S → S′). If any incorrect translation is found, the Verifier will undertake refinements to produce a revised translation of the premises and statement, denoted as P ′refined and S′refined.

Second, it will check whether the inference D adheres to valid log-ical rules. If any logical fallacy is detected, the Ver-ifier will conduct a refined derivation Drefined using the corrected logic rules. Consequently, these re-finements lead to the generation of a refined answer, represented as Crefined. Upon successful verifica-tion as Vvalidity(D/Drefined), the Verifier produces a verified answer Cverified.

读到这里，我在思考这些步骤是不是有点繁琐了。我觉得不用全放在verification这一步查的，而是一步一个verifier，不然solver也是根据错误的内容进行解决的。同时感觉这个框架解决困难问题的能力也有点有限

Experiment

Model.

Following prior work of Logic-LM (Pan et al., 2023), we assess the baselines and our method using GPT-3.5 (Ouyang et al., 2022) and GPT-4 (OpenAI, 2023)2, ensuring a fair comparison with identical model parameters.

很平民的实验了

Dataset.

Five standard datasets are employed, including PrOntoQA (Saparov and He, 2023), ProofWriter (Tafjord et al., 2021), FOLIO (Han et al., 2022), LogicalDeduction (Srivastava et al., 2022), and AR-LSAT (Zhong et al., 2022). Each of them takes different symbolic representations and introduces its own set of challenges in the topic of logical reasoning.

The primary metric：accuracy, measuring the multiple-choice correctness of the questions.

Symbolic Structure.

 FOL：In datasets PrOntoQA, ProofWriter, and FOLIO

 CO symbolic expression: in datasets LogicalDeduction and AR-LSAT.

Baseline

We compare with a range of established baselines.
Those based on GPT-3.5 are: 1) Naive Prompting; 2) CoT (Wei et al., 2022); 3) Logic-LM (Pan et al., 2023).
On GPT-4, apart from the above baselines, we further include more sys-tems: 4) CoT-SC (Wang et al., 2023b); 5) ToT (Yao et al., 2023); 6) Cumulative Reasoning (CR; Zhang et al., 2023a); 7) DetermLR (Sun et al., 2023);
Appendix extends more details of the symbolic structures (§B), the datasets (§C), and baselines (§D), as well as the full prompt configurations (§I).

Result

Ablation Study

Notably, the Planner and Solver components are identified as the most influential, enhancing performance by an average of 10.4%, followed by the Translator module, which facilitates a secondary improvement of 6.3%. The finding highlights the efficacy of our proposed plan-then-solve design for conquering the raw questions by dividing them into smaller ones.

Additionally, the use of symbolic representation and rules shows significant reasoning enhancement. 

Discussion

Performance on Complex Reasoning

Ours method has a significant en-hancement in the performance of the CoT. Intuitively, a greater depth indicates more complex problems. We analyzing the performance of different methods across varying levels of rea-soning depth. Observing Fig. 4, we notice that as the depth increases, the improvement over CoT becomes more pronounced, suggesting that our advantage lies in tackling more challenging issues. Moreover, even at a reasoning depth of 5, our method continues to achieve the best perfor-mance. 确实印证了我觉得这种symbolic表达在解决深层次逻辑的时候会出问题, 或者说提升有限

Robustness to Symbolic Syntax Error

In Fig. 5, we conduct a comparative analysis of our fully LLM-based reasoner against methods that rely on external resolvers, such as Logic-LM, specifically focusing on the success rate of executing symbolic expression syntax. 

对比点	Fully LLM-based	External Resolver-based
推理执行者	LLM 本身	外部工具（如Logic-LM， Z3、Prolog）
LLM 作用	端到端推理	自然语言转符号表达
易出错点	符号格式不严谨、逻辑不完整	翻译错误、信息缺失
可扩展性	随 LLM 进化而提升	易受“翻译能力”瓶颈限制

Benefit of Hybrid Expression of Symbolic And Natural Language

转换错误的原因↓

LLM’s translations from natural to symbolic lan-guage sometimes omit crucial information or introduce inaccuracies, leading to flawed symbolic representations. 

Our analysis, shown in Fig. 6, examines errors in cases wrongfully categorized as ‘unknown’ by external solvers on FOLIO. We identify that 55.6% of these errors were due to information loss (IL, 40.7%)—where essential details are missed—and information error (IE, 14.8%)—where translations are incorrect.  这里的处理思路是人工对不确定的内容进行分类

Implementing our methodology reduces these errors by 73.3%, with significant declines in IL and IE by 53.8% and 19.5%, respectively, cross-references both sym-bolic and natural language data to rectify transla-tion errors and bolster logical reasoning. (就相当于符号语言缺失的部分可以通过原文来补全，但是错误的信息可能没办法直接解决)

Reasoning Faithfulness

Often, LLMs may deliver correct answers through flawed reasoning, essentially reaching the right conclusion by luck.

Thus, we further assess the faithfulness of reasoning without a Verifier on the FOLIO dataset in Fig. 7.
’faithful’: if both the answer and the process are correct and logical;
’unfaithful’: if the answer is correct but the process is not;
’false’ if the answer it-self is incorrect.

To verify the logical validity of the reasoning process when the answer is correct, we employed manual evaluation.

This highlights the effectiveness of our methodology in enhancing the faithfulness of the reasoning process, with the Verifier serving to verify and refine reasoning steps. 

Impact of Using Different LLMs

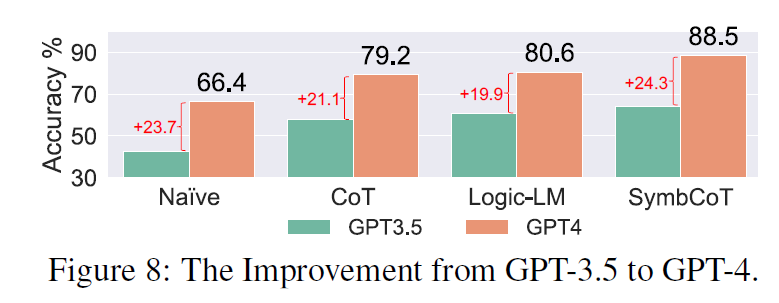
Our comparison of GPT-3.5 and GPT-4 on three FOL datasets (Fig. 8) shows the most performance boost (24.3%) with our method upon upgrading models. This underscores the synergy 协同作用 between our approach and more advanced models.

In contrast, methods like Logic-LM, which rely on external rule-based solvers, exhibit the least improvements with stronger models due to their dependence on LLMs for translation rather than reasoning.  Thus, although translation quality may improve, reason-ing capabilities remain unchanged as it is capped by external solvers. 感觉就是单纯的大模型本身比这种Loic-LM 要强hhh

Error analysis

The error analysis reveals that for an LLM to accu-rately complete a reasoning task, it requires two key capabilities:

1) The basic planning ability to identify the correct reasoning path

2) Upon identifying the reasoning path, ensure that each step of the reasoning is based on valid logic. 

The develop-ment of SymbCoT primarily enhances the second capability.
However, the first capability, planning, is equally crucial in problem-solving. 总之这个方法并没有优化模型的planning的部分，可以说是未来的改进空间

然后作者举了俩例子分别说明CoT会导致的逻辑谬误，以及Ecternal solver会导致的信息缺失，但是本文的方法可以解决

Conclusion

本研究提出符号思维链（Symbolic Chain-of-Thought, SymbCoT）框架，创新地将符号表达和逻辑规则与符号思维链提示相结合，以提高法学硕士的逻辑推理能力。具体来说，SymbCoT在主干LLM的基础上，将自然语言上下文翻译成符号格式，然后推导出一个循序渐进的方案，用符号逻辑规则来解决逻辑推理问题，然后由验证者来检查翻译和推理链。在FOL和CO符号表达的5个标准基准上的实验结果表明，SymbCoT在逻辑推理上显著增强了vanilla CoT。

Limitation& Future work

Firstly, we only evaluate two symbolic structures ( First-Order Logic, Constraint Optimization) in our framework. It is imperative to conduct fur-ther assessments on additional symbolic languages to ensure a comprehensive evaluation.

Secondly, the implementation of our framework is associated with considerable expenses. This financial impli-cation is attributed to the methodology of incorpo-rating symbolic rules, which inherently involves an extended reasoning chain and, consequently, the generation of an increased number of tokens by the model. 猜对了，果然引入符号规则（symbolic rules）会导致推理链变长、生成token数增多，从而带来额外的API费用或计算资源消耗。我在想plan过程是否也可以抽象？或者合并？不知道