栈与队列-

学习计划：3个月内算法小成，完成leetcode hot100

当前进度：学完数组、链表、哈希表、字符串、双指针

刷题语言：Python

时间：2025/04/02-2025/05/17

六、栈与队列

学习链接：代码随想录

1、栈与队列理论基础

• 栈：先进后出
• 队列：先进后出

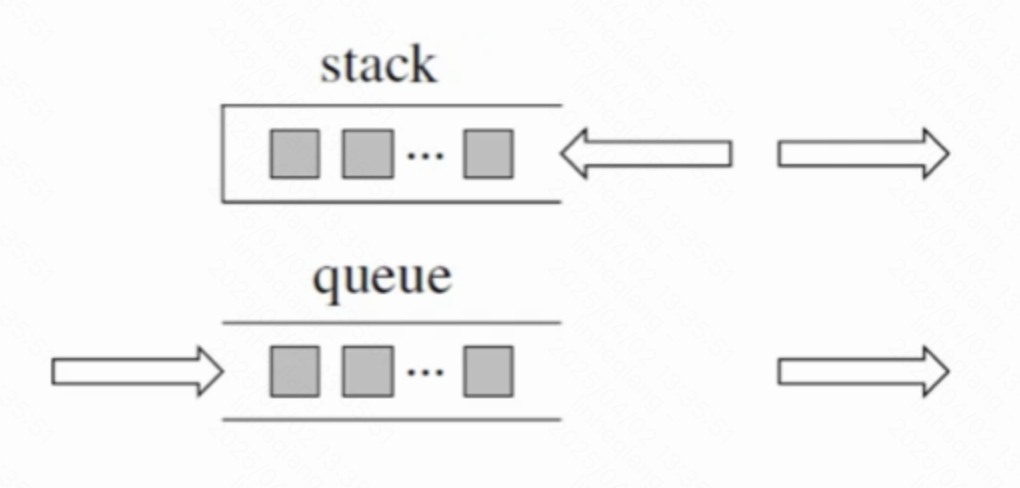
python基础：python中没有内置栈但是有列表List，队列使用deque

stack = []         #定义一个栈
stack.append(1)    #push进1，stack=[1]
stack.append(2)    #push进2，stack=[1,2]
out = stack.pop()  #pop栈顶，out=2,stack=[1]（后进先出）que = deque()      #定义一个队列
que.append(1)      #push进1，que=[1]
que.append(2)      #push进2，que=[1，2]
que.append(3)      #push进3，que=[1，2，3]
out = que.pop()    #pop队列，out=3，que=[1，2]
out = que.popleft()#popleft队列，out=1，que=[2]

2、用栈实现队列

使用栈实现队列的下列操作：

• push(x) -- 将一个元素放入队列的尾部。
• pop() -- 从队列首部移除元素。
• peek() -- 返回队列首部的元素。
• empty() -- 返回队列是否为空。

说明:

• 你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
• 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）。

思路：

        这是一道模拟题，不涉及到具体算法，考察的就是对栈和队列的掌握程度。使用栈来模拟队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。

        在push数据的时候，只要数据放进输入栈就好，但在pop的时候，操作就复杂一些，输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以了。

class MyQueue:def __init__(self):#in负责push，out负责popself.stack_in = []self.stack_out = []def push(self, x: int) -> None:#有新元素进来，放入inself.stack_in.append(x)def pop(self) -> int:#移除元素if self.empty(): #先判断空return Noneif self.stack_out: #如果stack_out有元素，从stack_out出return self.stack_out.pop()else:              #如果stack_out没有元素，先将stack_in一个个pop到stack_out，再从stack_out出for i in range(len(self.stack_in)):self.stack_out.append(self.stack_in.pop())return self.stack_out.pop()def peek(self) -> int:#获取队列开头tmp = self.pop()self.stack_out.append(tmp)  #pop出来后记得放回去return tmpdef empty(self) -> bool:#只有in或out有一个有元素就不为空return not (self.stack_in or self.stack_out)# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()

3、用队列实现栈

使用队列实现栈的下列操作：

• push(x) -- 元素 x 入栈
• pop() -- 移除栈顶元素
• top() -- 获取栈顶元素
• empty() -- 返回栈是否为空

注意:

• 你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
• 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
• 你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。

思路：一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

class MyStack:def __init__(self):self.que = deque()def push(self, x: int) -> None:self.que.append(x)def pop(self) -> int:if self.empty():return Nonefor i in range(len(self.que)-1):self.que.append(self.que.popleft())return self.que.popleft()def top(self) -> int:if self.empty():return Nonereturn self.que[-1]def empty(self) -> bool:return not self.que

4、有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 注意空字符串可被认为是有效字符串。

思路：这是一个对称匹配问题，由于栈结构的特殊性，非常适合做对称匹配类的题目。通过一次遍历，逐个把左括号加入栈中，如果遇到了匹配的右括号，则把左括号pop出，遍历结束刚好空栈表示这是有效的括号。

class Solution:def isValid(self, s: str) -> bool:stack=[]for item in s:#当遍历左符号时，把对应的右符号加入栈，方便匹配if item=='(':stack.append(')')elif item=='{':stack.append('}')elif item=='[':stack.append(']')#当遍历右符号时，如果不等于栈顶，或者栈是空，表示匹配失败elif not stack or stack[-1]!=item:return False#匹配成功则把对应的符号pop出，继续遍历else:stack.pop()#最后栈空为Truereturn True if not stack else False

5、删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

思路：使用栈来存放，那么栈的目的，就是存放遍历过的元素，当遍历当前的这个元素的时候，去栈里看一下我们是不是遍历过相同数值的相邻元素，一样的话表示重复，pop掉，最后剩下的就是没有相邻重复的了，拼接成字符串就行。

class Solution:def removeDuplicates(self, s: str) -> str:stack = []for item in s:if stack and item == stack[-1]:stack.pop()else:stack.append(item)return ''.join(stack)

6、逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。

有效的运算符包括 + ,  - ,  * ,  / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

思路：把元素逐个加入栈中，如果遇到运算符，则把栈最后2个元素拿出来计算，再把结果放进栈中。

class Solution:def evalRPN(self, tokens: List[str]) -> int:stack = []for item in tokens:if item not in {'+','-','*','/'}:stack.append(int(item)) #字符串转数字else:fig2 = int(stack.pop())fig1 = int(stack.pop())if item=='+':stack.append(fig1+fig2)elif item=='-':stack.append(fig1-fig2)elif item=='*':stack.append(fig1*fig2)elif item=='/':stack.append(fig1/fig2)return int(stack.pop())

7、滑动窗口最大值

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：你能在线性时间复杂度内解决此题吗？

思路：这是使用单调队列的经典题目，难点是如何求一个区间里的最大值呢？

1.暴力方法：遍历一遍的过程中每次从窗口中再找到最大的数值，这样很明显是O(n × k)的算法。

2.使用队列：队列内元素有序，最大值放在出队口，队列内没必要维护窗口内所有元素，只需要维护可能成为窗口内最大值的元素就可以了,所以每次队列加入新元素时，把队列中小于新元素的值都去掉，保证加入的元素永远是队列中的最小值，并且加在队列的右边（末尾），这样队列中永远从左到右都是从大到小的顺序，第一个元素就是最大值。弹出元素的时候只需要判断是否要弹出最大值即可。

class MyQueue:#单调队列，从大到小def __init__(self):self.queue = deque()def pop(self,value):#先判断queue是否为空#如果要弹出的元素=队列出口（最大）元素则弹出if self.queue and value == self.queue[0]:self.queue.popleft()def push(self,value):#先判断queue是否为空#push元素时，把小于要加入的元素都弹出，再把push，保证每次push入的都是队列中的最小值while self.queue and value>self.queue[-1]:self.queue.pop() #把右边最后一个元素弹出self.queue.append(value)def front(self):#队列中的最大值等于队列左边（出口）第一个元素return self.queue[0]class Solution(object):def maxSlidingWindow(self, nums, k):que = MyQueue() #单调队列res = []#先把第一个窗口的元素加入队列for i in range(k):que.push(nums[i])   #每次加入元素时，都会剔除掉队列中小于该元素的值，并且队列从大到小排列res.append(que.front()) #记录第一个窗口的最大值for i in range(len(nums)-k):#窗口每次滑动que.pop(nums[i])     #移除窗口最前面的元素que.push(nums[i+k])  #加入窗口后一个元素res.append(que.front())   #保存结果return res

8、前K个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

• 输入: nums = [1,1,1,2,2,3], k = 2
• 输出: [1,2]

示例 2:

• 输入: nums = [1], k = 1
• 输出: [1]

提示：

• 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
• 你的算法的时间复杂度必须优于 $O(n \log n)$ , n 是数组的大小。
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
• 你可以按任意顺序返回答案。

思路：