当前位置： 首页 > java >正文

5月13日复盘

java 2025/5/14 9:15:10

5月13日复盘

三、LSTM 模型

1. LSTM概述

长短期记忆网络（Long Short-Term Memory，LSTM）是一种特别设计来解决长期依赖问题的循环神经网络（RNN）架构。在处理序列数据，特别是长序列数据时，LSTM展现出其独特的优势，能够有效地捕捉和记忆序列中的长期依赖性。这一能力使得LSTM在众多领域，如自然语言处理、语音识别、时间序列预测等任务中，成为了一个强大且广泛使用的工具。

LSTM的核心思想是引入了称为“细胞状态”（cell state）的概念，该状态可以在时间步长中被动态地添加或删除信息。LSTM单元由三个关键的门控机制组成，通过这些门控机制，LSTM可以在处理长序列数据时更有效地学习长期依赖性，避免了传统RNN中的梯度消失或爆炸等问题。

所有循环神经网络都具有神经网络重复模块链的形式。在标准 RNN 中，这个重复模块将具有非常简单的结构，例如单个 tanh 层。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

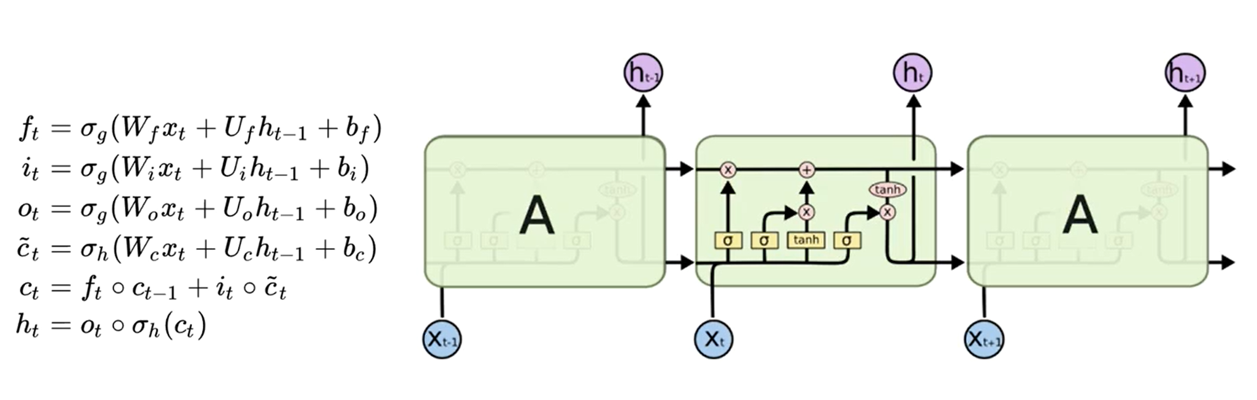
LSTM 也具有这种链式结构，但重复模块具有不同的结构。神经网络层不是单一的，而是四个（黄色矩形，四个激活函数，三个sigmod、一个tanh），以非常特殊的方式相互作用。

在这里插入图片描述

LSTM每个循环的模块内又有4层结构:3个sigmoid层，2个tanh层

在这里插入图片描述

基本状态

下图就是描述的关键部分：细胞状态C cell state

LSTM的关键是细胞状态CC，一条水平线贯穿于图形的上方，这条线上只有些少量的线性操作，信息在上面流传很容易保持。

在这里插入图片描述

细胞状态是LSTM的中心概念，它可以被视为一条信息的高速公路，沿着序列传递信息。细胞状态的设计使得信息可以几乎不受阻碍地在序列间流动，这解决了传统RNN中梯度消失问题导致的信息传递障碍。

门

LSTM有通过精心设计的称作“门”的结构来去除或者增加信息到细胞状态的能力。
门是一种让信息选择式通过的方法。他们包含一个sigmoid神经网络层和一个pointwise乘法操作。

在这里插入图片描述

Sigmoid层输出0到1之间的数值，描述每个部分有多少量可以通过。
0代表“不许任何量通过”
1代表“允许任何量通过”
LSTM 拥有三个门，来保护和控制细胞状态。

2. 门控机制

2.1 遗忘门

遗忘门（Forget Gate）：决定细胞状态中要保留的信息。它通过一个sigmoid函数来输出一个0到1之间的值，表示要忘记（0）或保留（1）的程度。1 代表“完全保留这个”，而 0 代表“完全摆脱这个”。

在这里插入图片描述

f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) ft​=σ(Wf​⋅[ht−1​,xt​]+bf​)

这个函数是遗忘门（forget gate）的公式，用于确定哪些信息应当从单元的状态中移除

  • [$ {h}{t-1}$, $ {x}{t} ] ：这是一个连接的向量，包括前一时间步的隐藏状态 ]：这是一个连接的向量，包括前一时间步的隐藏状态 ]：这是一个连接的向量，包括前一时间步的隐藏状态 {h}{t-1} 和当前时间步的输入 和当前时间步的输入 和当前时间步的输入 {x}{t}$。它们被合并起来，以便遗忘门可以考虑当前的输入和先前的隐藏状态来做出决策。
  • W f {W}_{f} Wf​：这是遗忘门的权重矩阵，用于从输入[$ {h}{t-1}$, $ {x}{t}$]中学习什么信息应该被遗忘。
  • b f {b}_{f} bf​：这是遗忘门的偏置项，它被加到权重矩阵和输入向量的乘积上，可以提供额外的调整能力，确保即使在没有输入的情况下遗忘门也能有一个默认的行为。
  • $\sigma $：这是sigmoid激活函数，它将输入压缩到0和1之间。在这里，它确保遗忘门的输出也在这个范围内，表示每个状态单元被遗忘的比例。
  • f t {f}_{t} ft​ ：这是在时间步 ( t ) 的遗忘门的输出，它是一个向量，其中的每个元素都在0和1之间，对应于细胞状态中每个元素应该被保留的比例。

函数的整体目的是使用当前输入和前一时间步的隐藏状态来计算一个门控信号，该信号决定细胞状态中的哪些信息应该被保留或丢弃。这是LSTM的关键特性之一，它允许网络在处理序列数据时学习长期依赖关系。

2.2 输入门

输入门（Input Gate）：决定要从输入中更新细胞状态的哪些部分。它结合了输入数据和先前的细胞状态，利用sigmoid函数来确定更新的量，并通过tanh函数来产生新的候选值，然后结合遗忘门确定最终的更新。

在这里插入图片描述

  1. 输入门的激活 ( i t {i} _{t} it​ )：

i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) it​=σ(Wi​⋅[ht−1​,xt​]+bi​)

  1. 候选细胞状态 ( C t {C}_{t} Ct​ )：

C ~ t = tanh ⁡ ( W C ⋅ [ h t − 1 , x t ] + b C ) \tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) C~t​=tanh(WC​⋅[ht−1​,xt​]+bC​)

解释如下：

  • i t {i} _{t} it​ 表示时间步 ( t ) 的输入门激活值，是一个向量。这个向量通过sigmoid函数产生，将值限定在 0 和 1 之间。它决定了多少新信息会被加入到细胞状态中。
  • W i {W}_{i} Wi​ 是输入门的权重矩阵，用于当前时间步的输入 x t {x}_{t} xt​ 和前一个时间步的隐藏状态 h t − 1 {h}_{t-1} ht−1​。
  • [$ {h}{t-1}$, $ {x}{t}$] 是前一个隐藏状态和当前输入的串联。
  • b i {b}_{i} bi​ 是输入门的偏置向量。
  • $ \widetilde{} {{C}_{t}}$ 是候选细胞状态，它是通过tanh函数产生的，可以将值限定在 -1 和 1 之间。它与输入门 i t {i}_{t} it​ 相乘，决定了将多少新的信息添加到细胞状态中。
  • W C {W}_{C} WC​ 是控制候选细胞状态的权重矩阵。
  • b C {b}_{C} bC​ 是对应的偏置向量。

2.3 状态更新

在这里插入图片描述

在每个时间步，LSTM单元都会计算这两个值，并结合遗忘门f_t的值更新细胞状态C_t。这样，LSTM能够记住长期的信息，并在需要的时候忘记无关的信息。

在这里插入图片描述

在计算新的细胞状态 ( C t {C}_{t} Ct​ ) 时使用的更新规则：

C t = f t ∗ C t − 1 + i t ∗ C ~ t C_t = f_t * C_{t-1} + i_t * \tilde{C}_t Ct​=ft​∗Ct−1​+it​∗C~t​

这里：

  • C t {C}_{t} Ct​ 是当前时间步的细胞状态。
  • C t − 1 {C}_{t-1} Ct−1​ 是上一个时间步的细胞状态。
  • f t {f}_{t} ft​ 是遗忘门的激活值，通过sigmoid函数计算得到。它决定了多少之前的细胞状态应该被保留。
  • i t {i}_{t} it​ 是输入门的激活值，也是通过sigmoid函数得到的。它决定了多少新的信息应该被存储在细胞状态中。
  • C t {C}_{t} Ct​ 是当前时间步的候选细胞状态，通过tanh函数得到。它包含了潜在的新信息，可以被添加到细胞状态中。

符号 * 代表元素间的乘积，意味着 f t {f}_{t} ft​ 和 i t {i}_{t} it​ 分别与 C t − 1 {C}_{t-1} Ct−1​ 和 C t {C}_{t} Ct​ 相乘的结果然后相加，得到新的细胞状态 C t {C}_{t} Ct​ 。这个更新规则使得LSTM能够在不同时间步考虑遗忘旧信息和添加新信息，是它在处理序列数据时记忆长期依赖信息的关键。

2.4 输出门

输出门（Output Gate）：决定在特定时间步的输出是什么。它利用当前输入和先前的细胞状态来计算一个输出值，然后通过sigmoid函数来筛选。

在这里插入图片描述

这个函数描述了LSTM（长短期记忆）网络的输出门和隐藏状态的计算。

  1. 输出门 o t {o}_{t} ot​ 的计算：

o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) ot​=σ(Wo​⋅[ht−1​,xt​]+bo​)

  1. 隐藏状态 h t {h}_{t} ht​ 的计算：

h t = o t ∗ tanh ⁡ ( C t ) h_t = o_t * \tanh(C_t) ht​=ot​∗tanh(Ct​)

具体来说：

  • o t {o}_{t} ot​ 是输出门的激活值。这是通过将前一时间步的隐藏状态 h t − 1 {h}_{t-1} ht−1​ 和当前时间步的输入 x t {x}_{t} xt​ 连接起来，并应用权重矩阵W_o以及偏置项 b_o，然后通过sigmoid函数 $\sigma $ 来计算的。Sigmoid函数确保输出值在0和1之间。

  • C t {C}_{t} Ct​ 是当前时间步的细胞状态，这是在之前的步骤中计算的。

  • C t {C}_{t} Ct​ 是细胞状态的tanh激活，这个激活函数将值压缩到-1和1之间。这是因为细胞状态C_t可以有很大的值，而tanh函数有助于规范化这些值，使它们更加稳定。

  • h t {h}_{t} ht​ 是当前时间步的隐藏状态，通过将输出门 o t {o}_{t} ot​ 的值与细胞状态的tanh激活相乘来得到。这个元素级别的乘法（Hadamard乘法）决定了多少细胞状态的信息将被传递到外部作为当前的隐藏状态输出。

这种结构允许LSTM单元控制信息的流动，它可以通过输出门来控制有多少记忆单元的信息会被传递到隐藏状态和网络的下一个时间步。

2.5 LSTM总结

在这里插入图片描述

3. 代码实现

基于 pytorch API 代码实现

在 LSTM 网络中，初始化隐藏状态 (h0) 和细胞状态 (c0) 是一个重要的步骤，确保模型在处理序列数据时有一个合理的起始状态。

h0 = torch.zeros(1, x.size(1), self.hidden_size)
c0 = torch.zeros(1, x.size(1), self.hidden_size)

1：指的是 LSTM 的层数。如果 num_layers > 1，那么这里应该是 num_layers。

x.size(1)：表示批次的大小 (batch_size)。这是输入 x 的第二个维度，因为 x 的形状为 (seq_len, batch_size, input_size)。

self.hidden_size：表示 LSTM 隐藏层的单元数，即隐藏状态和细胞状态的维度。

在 PyTorch 中，使用 LSTM (长短期记忆网络) 进行序列数据的处理时，调用 self.lstm(x, (h0, c0)) 会返回两个值：out 和 (hn, cn)。

out:

  • out 是 LSTM 网络在所有时间步的输出。
  • 假设输入 x 的形状是 (seq_len, batch_size, input_size)，那么 out 的形状将是 (seq_len, batch_size, num_directions * hidden_size)，其中 num_directions 是 1 如果 LSTM 是单向的，2 如果是双向的。
  • 具体地，out 包含 LSTM 在每个时间步的输出，适用于后续处理（例如，将其传递给一个全连接层）。

(_)或(hn, cn):

  • hn 是最后一个时间步的隐状态(hidden state)。

  • cn 是最后一个时间步的细胞状态(cell state)。

  • 如果输入 x 的形状是 (seq_len, batch_size, input_size)，那么 hn 和 cn 的形状将是 (num_layers * num_directions, batch_size, hidden_size)

    ​ 单层 LSTM：如果 num_layers = 1，LSTM 网络将只有一个层。这意味着输入序列直接通过这个单层 LSTM 进行处理。

    ​ 多层 LSTM：如果 num_layers > 1，LSTM 网络将有多层。输入序列首先通过第一层 LSTM，第一层的输出作为输入传递给第二层，以此类推，直到最后一层。

  • 这些状态可以用于初始化下一个序列的 LSTM，特别是在处理长序列或多个批次的序列数据时。

import torch
import torch.nn as nnclass LSTMMoudle(nn.Module):def __init__(self, input_size, hidden_size,out_size):super(LSTMMoudle, self).__init__()self.hidden_size = hidden_sizeself.input_size  = input_sizeself.out_size = out_sizeself.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, batch_first=True)self.fc = nn.Linear(hidden_size, out_size)def forward(self,x):out,(h_last,c_last) = self.lstm(x)#多对多输出#out = self.fc(out)#多对一输出out = torch.mean(out,dim=1)out = self.fc(out)return outif __name__ == '__main__':x = torch.randn(32, 10, 100)model = LSTMMoudle(100, 128, 5)out = model(x)print(out.shape)print(out)

4. 序列池化

在自然语言处理 (NLP) 中，序列池化（sequence pooling）是一种将变长序列转换为固定长度表示的方法。这个过程对于处理可变长度的输入（如句子或文档）特别有用，因为许多深度学习模型（如全连接层）需要固定长度的输入。

序列池化的主要方法包括：

最大池化（Max Pooling）：

  • 对序列中的每个特征维度，选择该维度的最大值作为输出。

  • 适用于突出序列中特定特征的最大激活值。

  • 例如，如果输入是长度为 5 的序列，且每个时间步的特征维度为 10，最大池化会对每个特征维度取最大值，输出形状为 (batch_size, feature_size)。

平均池化（Average Pooling）：

对序列中的每个特征维度，计算该维度的平均值作为输出。

适用于希望保留序列中所有特征的总体信息。

同样，对于长度为 5 的序列，特征维度为 10，平均池化会对每个特征维度取平均值，输出形状为 (batch_size, feature_size)。

注意力池化（Attention Pooling）：

  • 使用注意力机制对序列进行加权平均，根据每个时间步的重要性分配权重。
  • 适用于希望模型能够根据输入内容自适应地分配注意力权重。
  • 注意力池化的实现通常涉及一个注意力权重计算模块和一个对这些权重进行加权平均的模块。

5. 梯度消失

LSTM（长短期记忆网络）是一种特殊的RNN（循环神经网络），设计初衷就是为了解决传统RNN在长序列数据上训练时出现的梯度消失和梯度爆炸问题。然而，尽管LSTM相较于普通的RNN在处理长序列数据时表现得更好，但它仍然有可能在某些情况下出现梯度消失和梯度爆炸的问题。原因可以归结为以下几个方面：

5.1 梯度消失问题

梯度消失（Vanishing Gradient）主要在于反向传播过程中，梯度在多层传播时会逐渐减小，导致前面层的参数更新非常缓慢，甚至完全停滞。LSTM尽管通过门控机制（输入门、遗忘门和输出门）缓解了这个问题，但仍然可能出现梯度消失，特别是在以下情况下：

  • 长期依赖问题：如果序列特别长，即使是LSTM也可能无法有效地记住早期的信息，因为梯度会在很长的时间步长内持续衰减。
  • 不适当的权重初始化：如果权重初始化不合理，可能会导致LSTM的各个门在初始阶段就偏向于某种状态（如过度遗忘或完全记住），从而影响梯度的有效传播。
  • 激活函数的选择：尽管LSTM通常使用tanh和sigmoid激活函数，这些函数在某些输入值下可能会导致梯度的进一步缩小。

5.2 梯度爆炸问题

梯度爆炸（Exploding Gradient）则是在反向传播过程中，梯度在多层传播时会指数级增长，导致前面层的参数更新过大，模型难以收敛。LSTM在以下情况下可能出现梯度爆炸：

  • 过长的序列长度：即使是LSTM，在非常长的序列上仍然可能遇到梯度爆炸，因为梯度在反向传播时会不断累积，最终可能变得非常大。
  • 不适当的学习率：过高的学习率可能会导致梯度爆炸，因为参数更新的步伐太大，使得模型参数偏离最优解。
  • 不适当的权重初始化：与梯度消失类似，权重初始化也可能导致梯度爆炸。如果初始权重过大，梯度在反向传播过程中会不断放大。

解决方法

为了解决或缓解LSTM中的梯度消失和梯度爆炸问题，可以采取以下措施：

  • 梯度裁剪：在每次反向传播后，将梯度裁剪到某个阈值范围内，防止梯度爆炸。
  • 适当的权重初始化：使用标准的初始化方法，如Xavier初始化或He初始化，确保权重在初始阶段不至于过大或过小。
  • 调整学习率：选择合适的学习率，或者使用自适应学习率算法，如Adam、RMSprop等，动态调整学习率。
  • 正则化技术：如L2正则化、Dropout等，防止过拟合并平滑梯度。
  • 批归一化（Batch Normalization）：在网络层之间使用批归一化技术，可以加速训练并稳定梯度。

尽管LSTM通过其结构在一定程度上缓解了梯度消失和爆炸问题，但理解并应用这些技术和方法仍然是确保模型训练稳定和高效的关键。

四、GRU

1. 什么是GRU

​ 门控循环神经网络 (Gated Recurrent Neural Network，GRNN) 的提出，旨在更好地捕捉时间序列中时间步距离较大的依赖关系。它通过可学习的门来控制信息的流动。其中，门控循环单元 (Gated Recurrent Unit，GRU) 是一种常用的 GRNN。GRU 对LSTM 做了很多简化，同时却保持着和 LSTM 相同的效果。

2. GRU的原理

2.1 GRU 的两个重大改进

  1. 将三个门：输入门、遗忘门、输出门变为两个门：更新门 (Update Gate) 和 重置门 (Reset Gate)。
    1. 将 (候选) 单元状态 与 隐藏状态 (输出) 合并，即只有 当前时刻候选隐藏状态 和 当前时刻隐藏状态 。

2.2 模型结构

简化图：

内部结构：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传在这里插入图片描述

W z {W}_{z} Wz​ 、 W r {W}_{r} Wr​ 和 W是模型参数（权重矩阵），需要通过训练数据来学习。

GRU通过其门控机制能够有效地捕捉到序列数据中的时间动态，同时相较于LSTM来说，由于其结构更加简洁，通常参数更少，计算效率更高。

2.2.1 重置门

r t = σ ( W r ⋅ [ h t − 1 , x t ] ) r_t = \sigma(W_r \cdot [h_{t-1}, x_t]) rt​=σ(Wr​⋅[ht−1​,xt​])
重置门决定在计算当前候选隐藏状态时，忽略多少过去的信息。

2.2.2 **更新门 **

z t = σ ( W z ⋅ [ h t − 1 , x t ] ) z_t = \sigma(W_z \cdot [h_{t-1}, x_t]) zt​=σ(Wz​⋅[ht−1​,xt​])
更新门决定了多少过去的信息将被保留。它使用前一时间步的隐藏状态 ( h_{t-1} ) 和当前输入 ( x_t ) 来计算得出。

**2.2.3 候选隐藏状态 **

h ~ t = tanh ⁡ ( W ⋅ [ r t ∗ h t − 1 , x t ] ) \tilde{h}_t = \tanh(W \cdot [r_t * h_{t-1}, x_t]) h~t​=tanh(W⋅[rt​∗ht−1​,xt​])
候选隐藏状态是当前时间步的建议更新，它包含了当前输入和过去的隐藏状态的信息。重置门的作用体现在它可以允许模型抛弃或保留之前的隐藏状态。

在这里插入图片描述

**2.2.4 最终隐藏状态 **

在这里插入图片描述

h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ~ t h_t = (1 - z_t) * h_{t-1} + z_t * \tilde{h}_t ht​=(1−zt​)∗ht−1​+zt​∗h~t​
最终隐藏状态是通过融合过去的隐藏状态和当前候选隐藏状态来计算得出的。更新门 ${Z}_{t} $控制了融合过去信息和当前信息的比例。

在这里插入图片描述

h_{t}忘记传递下来的 h_{t-1}中的某些信息，并加入当前节点输入的某些信息。这就是最终的记忆。

http://www.xdnf.cn/news/5949.html

相关文章：

  • PAC文件：智能代理配置的瑞士军刀
  • rtty操作记录说明
  • 保险销售系统对接保险公司接口的常见技术架构
  • 阿里二面：聊聊 MySQL 主从同步方案的优缺点
  • 【兽医电子处方软件】佳易王宠物医院电子处方管理系统：宠物医院诊所用什么软件？一键导入配方模板软件程序实操教程 #操作简单 #宠物医院软件下载安装
  • C语言中的宏
  • 数控滑台：革新传统加工方式的利器
  • 谁在守护我们的危险时刻
  • C语言之旅5---分支与循环【2】
  • 学习第一遍 -- 第一章：SoC设计绪论
  • 从零开始掌握FreeRTOS（1）移植到STM32
  • uniapp+vue3+uview来开发我们的项目
  • 监控易运维：URL监控，守护Web业务的“哨兵”
  • 携程酒店 phantom-token token1004 分析
  • KT148A语音芯片发码很难播放_将4脚对地一下再发正常，什么原因？
  • C字符串的特点
  • 深度学习的相关术语介绍（杂乱版-想到啥介绍啥）
  • S7-1200 PLC与梅特勒-托利多IND360称重仪表通信
  • 使用聊天模型和提示模板构建一个简单的 LLM 应用程序
  • Protobuf工具
  • Hadoop是什么？（组件、特性、应用场景、生态系统等）
  • python文件打包成exe文件
  • 湖南大学3D场景问答最新综述！3D-SQA：3D场景问答助力具身智能场景理解
  • JS中获取选择器的方式：
  • 9.1 C#控制SW中零件的变色与闪烁
  • gdb调试
  • 山东大学软件学院计算机图形学2025期末考题回忆版
  • 使用class手搓Promise，三步一回头
  • 传输层协议UDP
  • latex公式格式