当前位置：首页 > java >正文

直方图详解

java 2025/5/13 10:25:24

1. 直方图概念(Histogram)

2. 词“histogram”的词源

3. 解释直方图

4. 例子

5. 直方图的数学定义

5.1 累积直方图(Cumulative histogram)

5.2 桶(箱)和宽度的数量

5.2.1 平方根的选择

5.2.1 Sturges公式

5.2.3 Rice法则

5.2.4 Doane公式

5.2.5 Scott正态参考法则

5.2.6 Terrell–Scott法则

5.2.7 Freedman–Diaconis 法则

5.2.8 最小化交叉验证估计平方误差(Minimizing cross-validation estimated squared error)

5.2.9 Shimazaki和Shinomoto的选择(Shimazaki and Shinomoto's choice)

5.2.10 可变桶宽(箱宽)

5.2.11 评注

1. 直方图概念(Histogram)

直方图是定量数据(quantitative data)分布的直观表示。要构建直方图，第一步是将值的范围“分箱(bin)”(或“分桶(bucket)”)——将整个值范围划分为一系列区间——然后计算每个区间内有多少个值。这些桶通常被指定为变量的连续、不重叠的区间。这些桶(区间)相邻，并且通常(但并非必须)大小相等。

直方图可以粗略地反映数据底层分布的密度(density)，通常用于密度估计(density estimation)：估计底层变量的概率密度函数。用于概率密度的直方图的总面积始终被归一化为 1。如果 x 轴上区间的长度均为 1，则直方图与相对频率图相同。

直方图有时会与条形图(bar charts)混淆。在直方图中，每个桶代表不同的值范围，因此整个直方图可以展示值的分布。但在条形图中，每个条形代表不同的观测类别(例如，每个条形可能代表不同的总体)，因此条形图可以用来比较不同的类别。一些作者建议条形图的条形之间应始终留有间隙，以表明它们不是直方图。

2. 词“histogram”的词源

“直方图”一词最初由数理统计学创始人Karl Pearson于1892年在伦敦大学学院的讲座中提出。Pearson的术语有时被错误地理解为将希腊语词根“γραμμα“(gramma，意为“图形”或“绘画”)与词根“ἱστορία”( historia，意为“探究”或“历史”)结合在一起。另一种解释是将词根“ἱστίον”(histion，意为“组织”) 结合起来，后者意为“网(web)”或“组织(tissue)”(例如在组织学中，即研究生物组织的学科)。这两种词源都是错误的，事实上，精通古希腊语的Pearson将这个术语衍生自另一个同音的希腊语词根“ἱστός”，意为“竖立的东西(something set upright)”、“桅杆(mast)”，指的是图表中的竖条。Pearson的新术语嵌入到了一系列类似的新词中，例如“stigmogram”(直方图)和“radiogram”(放射图)。

Pearson本人在1895年指出，尽管“直方图”一词是新词，但它所指的图形类型是“一种常见的图形表示形式”。事实上，使用条形图表示统计测量的技术是由苏格兰经济学家 William Playfair 在其1786年出版的《商业与政治地图集》中发明的。

3. 解释直方图

直方图对于理解数据分布的形状特别有用。直方图以图形方式相对客观地显示数据集中每个值出现的频率。直方图可以很容易地看出哪些值最常见，哪些值最不常见。在直方图中，横轴表示被测数据类型的值范围，纵轴表示每个区间内有多少个观测值。

bin——可译为“箱、桶、区间”。

Frequency (or count) of values that fall into each bin——落入每个桶中的值的频率(或计数)。

Number line——数线或数轴。

Tree circumference(mm)——树围(mm)(毫米)。

1 numeric variable——1 个数值变量。

直方图是数据集的直观表示，它显示数据集中每个值出现的频率。这些值沿 x 轴分组到不同的桶中。条形的高度表示数据集中有多少个值落入该桶中。在此示例中，直方图显示了随时间测量的橙树周长数据集中的所有树木周长值。这 35 个周长值被分成五个桶：第一个桶包含周长为 0 至 49 毫米的树木；第二个桶包含周长为 50 至 99 毫米的树木；第三个桶包含周长为 100 至 149 毫米的树木；第四个桶包含周长为 150 至 199 毫米的树木；最后一个桶包含周长为 200 至 250 毫米的树木。橙色条的高度表示每个桶中有多少棵树。蓝色文字描述了直方图的常见组成部分。在本例中，数值变量的数轴是 x 轴。

此类数据可视化有助于回答以下问题：

(1) 数据的中心在哪里？

(2) 数据的分布情况如何？数据的范围是多少？

(3) 数据的形状如何？例如，它是对称的、倾斜的、均匀的还是双峰的？

(4) 两个(或多个)数据集之间的差异有多大？

观察直方图时，请务必注意以下几点：

(1) 数轴(通常是 x 轴)跨越数据集中某个数值变量的最小值和最大值。

(2) 这条数轴被分成大小相等的区间(interval)，称为桶 (bin)，涵盖数据中值的范围。

(3) 直方图显示某个值落入特定桶的频率。

(4) 每条柱状图的高度表示数据集中落入特定桶的值的数量。

(5) 当 y 轴标记为“计数”或“数值”时，y 轴上的数字往往是离散的正整数。每条柱状图的高度表示落入每个区间的数据点数量。

(6) 当 y 轴标记为“相对频率”时，y 轴上的数字往往在 0 到 1.0 之间，或 0 到 100% 之间。每条柱状图的高度表示落入每个区间的值的比例或百分比。

(7) 直方图可以轻松显示数据集中哪些值最常见，哪些值最不常见。

(8) 直方图在视觉上与条形图有所不同。直方图的条形之间没有间隙，而条形图的条形之间有间隙。

4. 例子

(1) 使用了 500 个项的直方图。

桶/区间	数量/频率
−3.5 至 −2.51	9
−2.5至−1.51	32
−1.5至−0.51	109
−0.5至0.49	180
0.5至1.49	132
1.5至2.49	34
2.5至3.49	4

-----------------------------------x的直方图----------------------------------

(2) 用于描述直方图中模式的词语有：“对称(symmetric)”、“左偏(skewed left)”或“右偏(skewed right)”、“单峰模式(unimodal)”、“双峰模式(bimodal)”或“多峰模式(multimodal)”。

--------------------------------------------------对称，单峰---------------------------------------------

---------------------------------------------------右斜--------------------------------------------------

---------------------------------------------------左斜---------------------------------------------

------------------------------------------------双峰------------------------------------------------

----------------------------------------------多峰-----------------------------------------------

-------------------------------------------对称------------------------------------------------

(3) 为了更好地理解数据，最好使用几种不同的桶宽来绘制数据。以下是一个关于餐厅小费的示例。

----------------------------------使用 1美元桶宽、右斜、单峰的提示------------------------------------

------------------------------使用 10厘米桶宽的提示，仍然右斜，多峰，模式为美元和50美分金额，表示四舍五入，也有一些异常值-----------------------------

(4) 美国人口普查局发现，有1.24亿人外出工作。下表根据其通勤时间数据，显示回答“至少30分钟但少于35分钟”通勤时间的人数绝对值高于其上下类别的人数。这可能是由于人们对报告的通勤时间进行了四舍五入。在收集民众数据时，将数值报告为略显随意的四舍五入数字是一个常见现象。

绝对数字数据

桶/区间	宽度	数量	数量/宽度
0	5	4180	836
5	5	13687	2737
10	5	18618	3723
15	5	19634	3926
20	5	17981	3596
25	5	7190	1438
30	5	16369	3273
35	5	3212	642
40	5	4122	824
45	15	9200	613
60	30	6461	215
90	60	3435	57

-------------------------美国 2000 年人口普查上班时间直方图。曲线下面积等于案例总数。此图使用了表格中的 Q/宽度。(通勤时间单位：分钟)--------------------------

该直方图将单位区间内的案例数显示为每个区块的高度，因此每个区块的面积等于调查中属于该类别的人数。曲线下的面积代表案例总数(1.24亿)。此类直方图显示的是绝对数字，Q以千为单位。

(5) 按比例的数据

桶/区间	宽度	数量(Q)	数量/总数/宽度(表示除以)
0	5	4180	0.0067
5	5	13687	0.0221
10	5	18618	0.0300
15	5	19634	0.0316
20	5	17981	0.0290
25	5	7190	0.0116
30	5	16369	0.0264
35	5	3212	0.0052
40	5	4122	0.0066
45	15	9200	0.0049
60	30	6461	0.0017
90	60	3435	0.0005

此直方图与第一个直方图仅在垂直尺度上有所不同。每个块的面积是每个类别所占总数的分数，所有条形的总面积等于 1(分母表示“全部”)。显示的曲线是简单的密度估计值。此版本显示比例，也称为单位面积直方图。

换言说，直方图用矩形表示频率分布，矩形的宽度表示类距(class intervals)，面积与相应的频率成正比：每个矩形的高度表示该类距的平均频率密度。这些类距被放在一起，是为了表明直方图所表示的数据虽然互不相容，但也是连续的。(例如，在直方图中，可以存在 10.5-20.5 和 20.5-33.5 两个相连的类距，但不能存在 10.5-20.5 和 22.5-32.5 两个相连的类距。空类距表示为空，不会被跳过。)

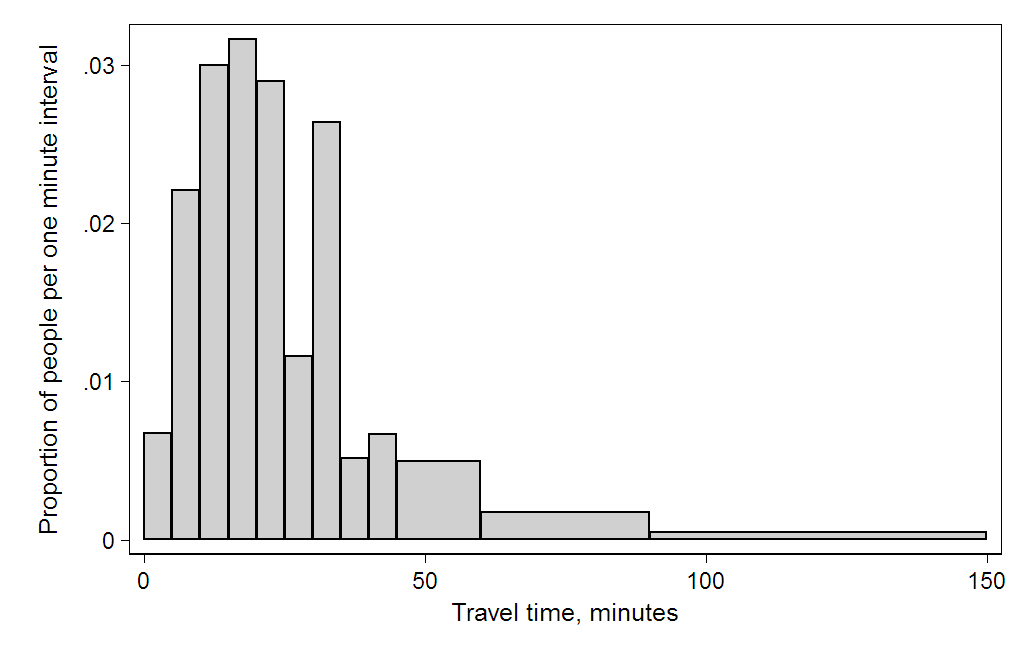
-------------------------------2000 年美国人口普查上班时间直方图。曲线下面积为 1。此图使用表格中的 Q/总面积/宽度(拥挤程度)。方块高度代表拥挤程度，定义为每水平单位的百分比。--------------------------------------------------------

5. 直方图的数学定义

用于构建直方图的数据是通过函数 $m_{i}$ 生成的，该函数计算落入每个不相交类别(称为 “桶或箱(bin)”)的观测值数量。因此，如果我们设 n 为观测值总数，k 为桶总数，则直方图数据 $m_{i}$ 满足以下条件：

$\displaystyle n = \sum_{i=0}^{k}m_{i}$ 。(译注：即直方图曲线下的总面积。)

直方图可以被认为是一种简化的核密度估计，它使用核函数来平滑区间的频率。这样可以得到更平滑的概率密度函数，通常能够更准确地反映基础变量的分布。密度估计可以作为直方图的替代绘制，通常绘制为曲线而不是一组框。然而，当需要对直方图的统计特性进行建模时，直方图在应用中是首选。核密度估计的相关变化很难用数学描述，而对于每个区间独立变化的直方图来说，描述起来则很简单。

核密度估计的替代方法是平均平移直方图，它计算速度快，并且无需使用核即可给出密度的平滑曲线估计。

5.1 累积直方图(Cumulative histogram)

累积直方图：一种映射，用于统计指定直方图前所有直方图中观测值的累积数量。例如，直方图 $m_{i}$ 的累积直方图 $M_{i}$ 可以定义为：

$\displaystyle M_{i} = \sum_{j=1}^{i}m_{i}$ 。

5.2 桶(箱)和宽度的数量

没有“最佳”的桶数，不同的桶宽可以揭示数据的不同特征。数据分组至少与17世纪Graunt的研究一样古老，但直到1926年Sturges的研究才出现系统的指导原则。

在底层数据点密度较低的情况下，使用较宽的桶宽可以降低采样随机性造成的噪声；在密度较高的情况下，使用较窄的箱宽(这样信号会淹没噪声)可以提高密度估计的精度。因此，在直方图中改变桶宽可能会有所帮助。尽管如此，等宽桶宽仍然被广泛使用。

一些理论家尝试确定最佳的桶宽，但这些方法通常对分布的形状做出了严格的假设。根据实际数据分布和分析目标，不同的桶宽可能更合适，因此通常需要进行实验来确定合适的宽度。然而，也存在各种有用的指导原则和经验法则。

桶数 k 可以直接指定，也可以根据建议的桶宽 h 计算得出：

$\displaystyle k =\left \lceil \frac{\mathsf{max}{(x)}-\mathsf{min}(x)}{h} \right \rceil$ (括号表示上限)。

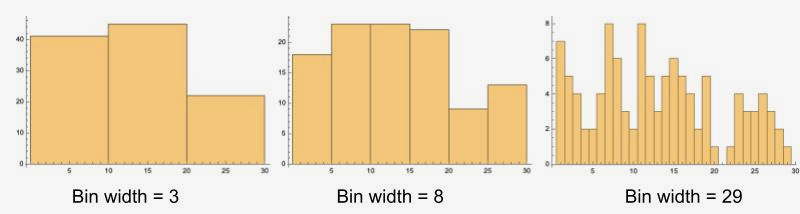
------------------------------------------用不同的桶宽表示的直方图数据-----------------------------

5.2.1 平方根的选择

$\displaystyle k=\left \lceil \sqrt{n} \:\:\right \rceil$ 。

对样本中数据点的数量取平方根，并四舍五入到下一个整数。许多基础统计学教科书都提出了这条规则，并且它被广泛应用于许多软件包中。

5.2.1 Sturges公式

Sturges 规则源自二项分布(binomial distribution)，并隐式假设了近似正态分布(normal distribution)。

$\displaystyle k = \left \lceil \log_{2}{n} \right \rceil + 1$ 。

Sturges公式隐式地根据数据的范围确定了分桶大小，如果 n < 30，其性能可能会很差，因为分桶数量会很少(少于 7 个)，而且不太可能很好地显示数据的趋势。另一方面，对于非常大的数据集，Sturges公式可能会高估分桶宽度，导致直方图过于平滑。如果数据不服从正态分布，其性能也可能很差。

与另外两个被广泛接受的直方图分桶公式 Scott规则和Terrell-Scott 规则相比，当 n ≈ 100 时，Sturges公式的输出最接近。

5.2.3 Rice法则

$\displaystyle k = \left \lceil \: 2\sqrt[3]{n} \:\: \right \rceil$ 。

Rice法则是作为 Sturges 法则的一个简单替代法则提出的。

5.2.4 Doane公式

Doane 公式是 Sturges 公式的修改版，其试图提高其处理非正态数据的性能。

$\displaystyle k = 1 + \log_{2}{(n)}+ \log_{2}\left ( 1+\frac{|g_{1}|}{\sigma_{g_{1}}} \right )$ ，

其中， $g_{1}$ 是估计的分布的三阶矩偏度(3rd-moment-skewness)而

$\displaystyle \sigma_{g_{1}}=\sqrt{\frac{6(n-2)}{(n+1)(n+3)}}$ 。

5.2.5 Scott正态参考法则

符宽度 h 为

$\displaystyle h=\frac{3.49\widehat{\sigma}}{\sqrt[3]{n}}$ ，

其中 $\widehat{\sigma}$ 是样本标准差。Scott 正态参考规则对于正态分布数据的随机样本是最优的，因为它可以最小化密度估计的积分均方误差。这是 Microsoft Excel 中使用的默认规则。

5.2.6 Terrell–Scott法则

$\displaystyle k= \left \lceil \sqrt[3]{2n} \right \rceil$ 。

Terrell-Scott 法则并非正态参考法则。它给出了渐近最优直方图所需的最小区间数，其中最优性通过积分均方误差来衡量。该界限是通过寻找“最平滑”的可能密度得出的，该密度为 $\frac{3}{4}(1-x^{2})$ 。任何其他密度都需要更多的区间，因此上述估计也称为“过度平滑”规则。这两个公式的相似性，以及 Terrell 和 Scott 在提出该规则时都在Rice大学的事实，表明这也是Rice法则的起源。

5.2.7 Freedman–Diaconis 法则

Freedman-Diaconis 法则给出的桶宽 h 为：

$\displaystyle h = 2\frac{\mathsf{IQR}(x)}{\sqrt[3]{n}}$ ，

它基于四分位距(interquartile range)，用 IQR 表示。它用 2IQR 取代了 Scott法则的 3.5σ，后者对数据异常值的敏感度低于标准差。

5.2.8 最小化交叉验证估计平方误差(Minimizing cross-validation estimated squared error)

这种最小化Scott法规中的综合均方误差的方法，可以推广到正态分布之外，即通过使用留一交叉验证(leave-one out cross validation)：

$\displaystyle \mathop{\arg\min}_{h}{\hat{J}(h)}= \mathop{\arg\min}_{h}{\left (\frac{2}{(n-1)h}-\frac{n+1}{n^{2}(n-1)h}\Sigma_{k}{N_{k}^{2}} \right )}$ ，

此处 $N_{k}$ 是第 k 个桶中的数据点数，选择最小化 J 的 h 值将最小化积分均方误差。

5.2.9 Shimazaki和Shinomoto的选择(Shimazaki and Shinomoto's choice)

该选择基于估计的 $L^{2}$ 风险函数的最小化

$\displaystyle \mathop{\arg\min}_{h}{{\frac{2\overline{m}-v}{h^{2}}}}$ ，

其中， $\overline{m}$ 和v 分别是均值和箱宽为 h 的直方图的偏方差(biased variance), $\overline{m}=\frac{1}{k}\Sigma_{i=1}^{k}m_{i}$ ， $v=\frac{1}{k}\Sigma_{i=1}^{k}\left (m_{i}-\overline{m} \right )^{2}$ 。

5.2.10 可变桶宽(箱宽)

对于某些应用，与其选择等距的桶宽，不如改变桶。这样可以避免出现计数较低的桶。一种常见的情况是选择等概率桶，其中每个桶的样本数量预计大致相等。桶可以根据某个已知分布选择，也可以根据数据选择，使得每个桶包含 ≈ n/k个样本。绘制直方图时，频率密度用作因变量轴。虽然所有桶的面积大致相等，但直方图的高度近似于密度分布。

对于等概率桶，建议桶数遵循以下法则：

$k=2n^{2/5}$ 。

选择这样的桶是为了最大化Pearson chi平方检验的功效，该检验用于检验桶是否包含相等数量的样本。更具体地说，对于给定的置信区间 α ，建议选择以下等式的 1/2 到 1 倍之间的值：

$\displaystyle k=4\left (\frac{2n^{2}}{\Phi^{-1}(\alpha)} \right )^{\frac{2}{5}}$ ，

其中， $\Phi^{-1}(\alpha)$ 是概率单位函数(probit function)。按照这个法则，α = 0.05 就会得出介于 $1.88n^{2/5}$ 与 $3.77n^{2/5}$ 之间的数；从这个广泛的最优值中选择系数 2 作为一个容易记住的值。

5.2.11 评注

桶数量应与 $\sqrt[3]{n}$ 成正比的一个合理理由是：假设数据为 n个具有平滑密度的有界概率分布的独立实现。那么，当 n 趋向于无穷大时，直方图仍然同样“粗糙”。如果 s 是分布的“宽度”(例如，标准差或四分位距(inter-quartile range))，则桶中的单位数(频率)的阶(order)为 $\sqrt{s/(nh)}$ ，相对标准误差的阶数为 $\sqrt{s/(nh)}$ 。与下一个桶相比，如果密度的导数非零，则频率的相对变化阶数为 h/s 。如果 h 的阶数为 $s/\sqrt[3]{n}$ ，则这两个阶数相同，因此 k 的阶数为 $\sqrt[3]{n}$ 。这种简单的立方根选择方法也适用于宽度非恒定的桶。