当前位置：首页 > java >正文

图神经网络分享系列-LINE(三)

java 2025/8/23 9:07:21

一、实验

1、实验设置

1、数据集

2、算法比较

1、图分解（GF）

2、DeepWalk

3、LINE-SGD

4、 LINE

5、LINE (1st+2nd)

3、参数设置

2、定量结果

1、语言网络

1、词类比任务

1、实验设置与结果

2、性能分析

3、计算效率

2、文本分类

1、实验结果

2、邻近性分析

编辑

2、社交网络

1、Flickr网络

2、Youtube网络

3、引文网络

1、DBLP（作者引文）网络

2、DBLP（论文引文）网络

3、网络布局

4、网络稀疏性对性能的影响

5、参数敏感性

6、扩展性

二、总结

紧接着上一篇：图神经网络分享系列-LINE(二)-CSDN博客

图神经系列概览：图神经网络分享系列-概览-CSDN博客

我们一起来看下论文的实验部分

一、实验

我们对LINE的有效性和效率进行了实证评估。该方法被应用于多种类型的大规模现实网络，包括一个语言网络、两个社交网络和两个引文网络。

1、实验设置

1、数据集

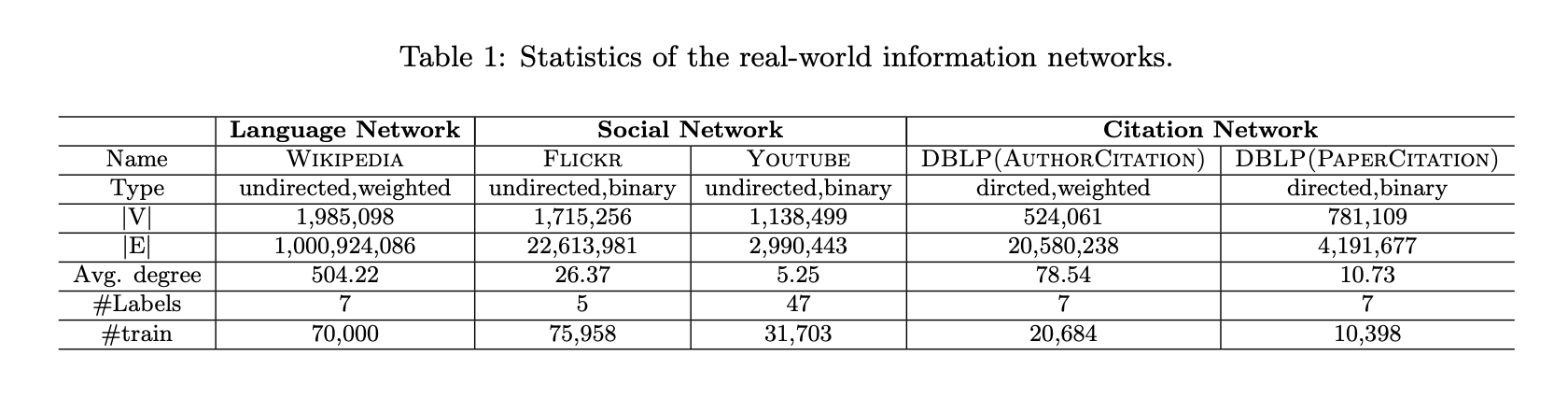
（1）语言网络：基于英文维基百科全部页面构建了一个词语共现网络。在每个5词滑动窗口内的词语被视为相互共现，同时过滤掉出现频率低于5次的词语。

（2）社交网络：使用了两个社交网络——Flickr和YouTube。Flickr网络的密度高于YouTube网络（与DeepWalk[16]使用的网络相同）。

（3）引文网络：包含两种类型——作者引文网络和论文引文网络。通过DBLP数据集[19]构建了作者间及论文间的引文关系网络。作者引文网络记录了某位作者的论文被另一位作者引用的次数。

这些网络的详细统计信息汇总于表1，涵盖了多种信息网络类型（有向/无向、二元/加权）。每个网络至少包含50万个节点和数百万条边，其中最大的网络规模达到约200万个节点和10亿条边。

2、算法比较

我们比较了LINE模型与多种现有的大规模网络图嵌入方法，但未涵盖MDS、IsoMap和拉普拉斯特征映射等经典算法，因其无法处理此类规模网络。

1、图分解（GF）

基于矩阵分解的图分解技术将信息网络表示为亲和矩阵，通过矩阵分解生成低维向量表示。该方法采用随机梯度下降优化，适用于大规模网络，但仅能处理无向图。

2、DeepWalk

该方法针对社交网络嵌入设计，仅适用于二元边网络。通过从顶点出发的截断随机游走获取上下文信息，因此仅利用二阶邻近性。

3、LINE-SGD

该模型直接通过随机梯度下降优化目标函数（式3或式6，上一篇文章中），采样边时将边权直接乘入梯度更新。含两个变体：使用一阶邻近性的LINE-SGD(1st)和使用二阶邻近性的LINE-SGD(2nd)。

4、 LINE

采用论文4.2节(上篇文章)提出的边采样优化策略，每步按边权比例采样边并视作二元边进行模型更新。包含两个变体：LINE(1st)和LINE(2nd)。与图分解类似，LINE(1st)和LINE-SGD(1st)仅适用于无向图，而LINE(2nd)和LINE-SGD(2nd)同时适用于有向和无向图。

5、LINE (1st+2nd)

为联合利用一阶和二阶邻近性，可将LINE(1st)和LINE(2nd)学习到的向量拼接成长向量，并对维度重新加权以平衡两种表示。监督学习任务中权重可通过训练数据自动确定，无监督场景下权重设置较困难，因此该变体仅用于监督任务场景。

3、参数设置

随机梯度下降（SGD）的小批量（mini-batch）大小统一设置为1。参照文献[13]，学习率的初始值设为ρ0 = 0.025，并按公式ρt = ρ0 (1−t/T)动态调整，其中T为小批量或边样本的总数。

语言网络的嵌入维度默认设置为200，与词嵌入模型[13]保持一致；其他网络的嵌入维度默认为128，参照文献[16]。其余默认参数如下：

LINE和LINE-SGD的负采样数K = 5；
LINE(1st)和LINE(2nd)的总样本量T = 100亿，GF的T = 200亿；
DeepWalk的窗口大小win = 10、游走长度t = 40、每个顶点的游走次数γ = 40；
所有嵌入向量最终通过L2归一化（||w⃗||2 = 1）处理。

2、定量结果

1、语言网络

该语言网络包含200万个节点和10亿条边。通过两个应用场景评估学习嵌入的效果：词语类比和文档分类。

1、词类比任务

该任务由Mikolov等人提出。给定一个词对（a, b）和单词c，目标是找到单词d，使得c与d之间的关系类似于a与b之间的关系，记作 a : b → c : ?。例如，给定词对（“中国”，“北京”）和单词“法国”，正确答案应为“巴黎”，因为“北京”是“中国”的首都，而“巴黎”是“法国”的首都。基于词向量，该任务通过找到与向量 ⃗u_b − ⃗u_a + ⃗u_c 余弦相似度最高的词嵌入 ⃗u_d 来解决，即：d∗ = argmax_d cos((⃗u_b − ⃗u_a + ⃗u_c), ⃗u_d)。词类比任务分为两类：语义类比和句法类比。

1、实验设置与结果

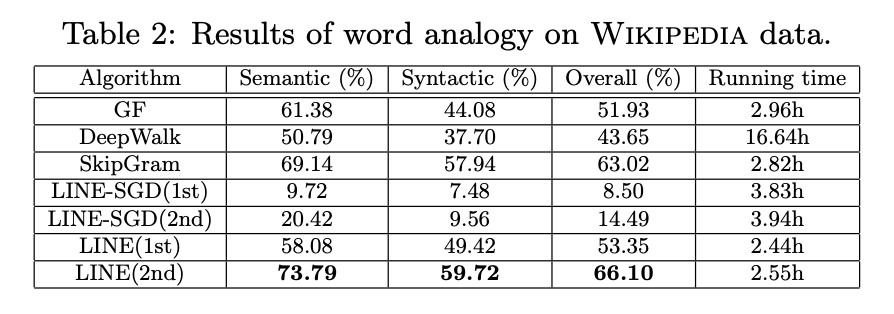
表2展示了在维基百科语料库（Skip-Gram）或维基百科词网络（其他方法）上学习到的词嵌入的类比任务结果。

图分解方法：词对间权重定义为共现次数的对数，性能优于直接使用原始共现值。
DeepWalk：尝试不同截断阈值将语言网络转换为二值网络，保留所有边时性能最佳。
Skip-Gram：作为当前最优词嵌入模型，直接从维基百科页面学习词嵌入，本质上是隐式矩阵分解方法，窗口大小为5（与语言网络构建一致）。

2、性能分析

LINE(2nd) 优于所有其他方法（包括图嵌入方法和Skip-Gram），表明二阶邻近性比一阶邻近性更能捕捉词义。二阶邻近性高的词在相同上下文中可互换，其语义相似性比一阶共现更强。
LINE(2nd)超越Skip-Gram的原因：语言网络比原始词序列更能捕捉全局共现结构。
其他方法对比：图分解和LINE(1st)显著优于DeepWalk，尽管DeepWalk探索了二阶邻近性，但其忽略了语言网络中关键的边权重（共现次数）。
LINE-SGD的缺陷：直接使用SGD优化的LINE模型性能较差，因语言网络中边权重差异过大（从个位数到数万），导致学习过程不稳定。通过边采样处理的LINE模型有效解决了此问题，无论使用一阶或二阶邻近性均表现良好。

3、计算效率

所有模型在单机（1TB内存、40核2.0GHz CPU、16线程）上运行：

LINE(1st)和LINE(2nd) 处理含200万节点和10亿边的网络耗时不足3小时，比图分解快至少10%，远优于DeepWalk（速度慢5倍）。
LINE-SGD稍慢的原因：需采用阈值截断技术防止梯度爆炸。

2、文本分类

另一种评估词嵌入质量的方法是利用词向量计算文档表示，并通过文档分类任务进行评估。为获取文档向量，采用了一种简单的方法：对文档中所有词向量的表示取平均值。这种方法旨在比较不同词嵌入方法的优劣，而非寻找最佳的文档嵌入方法。更先进的文档嵌入方法可参考相关文献[7]。

实验数据来源于维基百科页面摘要（http://downloads.dbpedia.org/3.9/en/long_abstracts_en.nq.bz2）及其分类标签（http://downloads.dbpedia.org/3.9/en/article_categories_en.nq.bz2）。选取了7个多样化类别进行分类，包括“艺术”“历史”“人类”“数学”“自然”“技术”和“体育”。每个类别随机抽取10,000篇文章，同时排除属于多个类别的文章。通过随机采样不同比例的已标注文档用于训练，其余部分用于评估。

所有文档向量输入至LibLinear包训练的一对多逻辑回归分类器，并采用Micro-F1和Macro-F1作为分类指标。结果通过10次不同训练数据采样取平均值。

1、实验结果

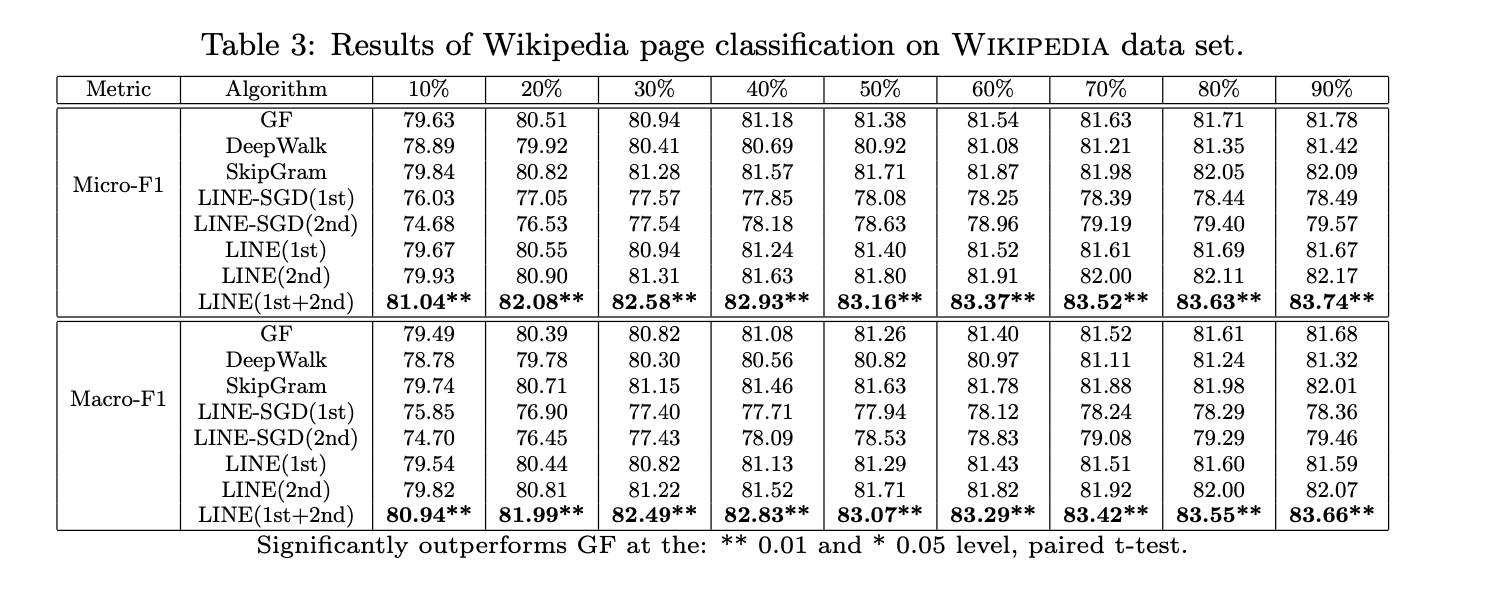
表3展示了维基百科页面分类结果。与词类比任务结论相似：

图分解方法因考虑边权重而优于DeepWalk（后者忽略边权重）。
基于SGD优化的LINE方法因边权重发散问题表现较差，但通过边采样优化后显著提升。
LINE（二阶邻近）优于LINE（一阶邻近）和图分解方法。
结合一阶与二阶邻近的LINE(1st+2nd)方法性能显著超越其他方法，表明两种邻近性互补。

2、邻近性分析

表4比较了一阶与二阶邻近性下与给定词最相似的词：

二阶邻近返回的相似词均与目标词语义相关。
一阶邻近返回的相似词混合了语法和语义相关性。

2、社交网络

与语言网络相比，社交网络的稀疏程度更高，尤其是Youtube网络。通过多标签分类任务评估顶点嵌入效果，该任务将每个节点分配到一个或多个社区。随机选取不同比例的顶点作为训练集，其余用于评估，结果取10次运行的平均值。

1、Flickr网络

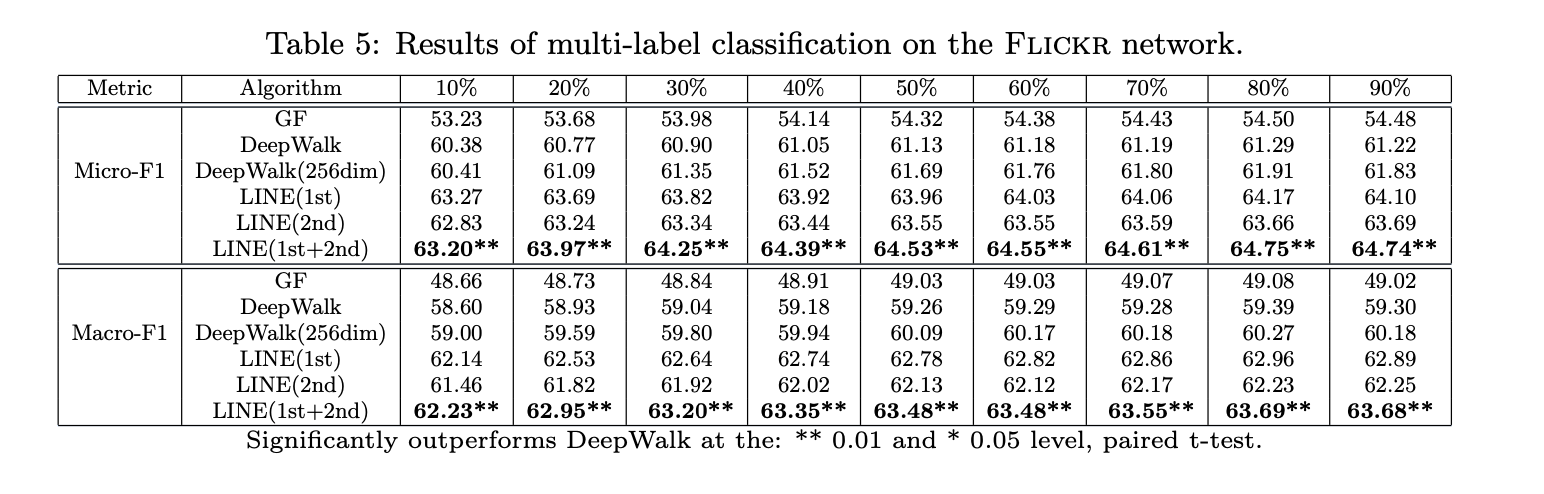
观察Flickr网络上的结果，选择最热门的5个社区作为多标签分类的顶点类别。表5显示，LINE（一阶+二阶）显著优于其他方法。LINE（一阶）略优于LINE（二阶），这与语言网络的结果相反。原因有二：

社交网络中一阶邻近性仍比二阶更重要，表明强连接关系占主导；
当网络过于稀疏且节点平均邻居数过少时，二阶邻近性可能变得不准确。
LINE（一阶）优于图分解法，表明其对一阶邻近性建模能力更强；LINE（二阶）优于DeepWalk，说明其更擅长捕捉二阶邻近性。将两者嵌入表示拼接后性能进一步提升，证实两种邻近性具有互补性

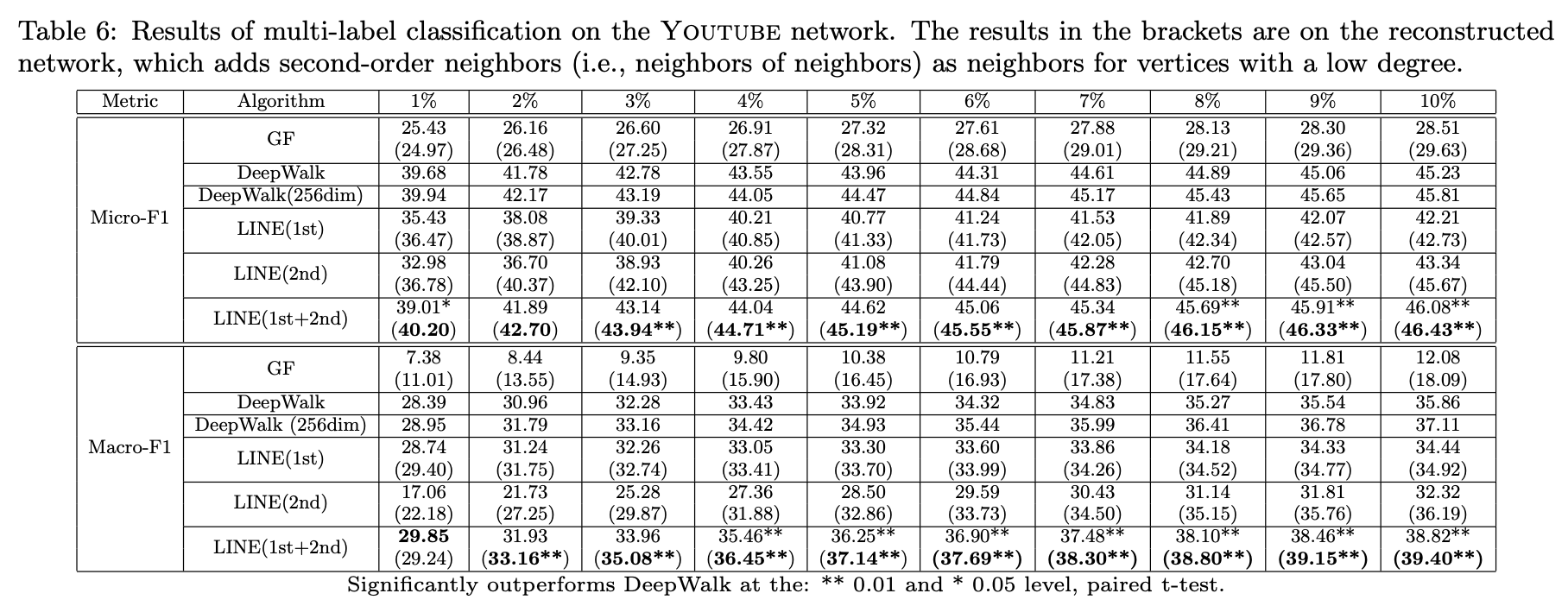
2、Youtube网络

表6展示了极度稀疏的Youtube网络结果（平均度数仅5）。在不同训练数据比例下，LINE（一阶）大多优于LINE（二阶），与Flickr结论一致。由于极端稀疏性，LINE（二阶）甚至表现不及DeepWalk。但结合一阶与二阶表示后，LINE在128或256维下均超越DeepWalk，再次验证两种邻近性能协同缓解网络稀疏问题。

值得注意的是，DeepWalk通过截断随机游走间接丰富节点上下文，类似深度优先搜索。该方法虽能快速缓解局部稀疏性，但可能引入远距离无关节点。更合理的策略是采用广度优先搜索递归扩展邻居节点。实验中对度数小于1000的节点进行邻居扩展直至达到1000节点规模，发现继续增加节点数不会提升效果。

表6括号内结果为重构网络上的性能，图分解、LINE（一阶/二阶）均有所提升，其中LINE（二阶）在多数情况下反超DeepWalk。但LINE（一阶+二阶）在重构网络上提升有限，说明原始网络中两种邻近性的组合已能捕获大部分信息。这表明LINE（一阶+二阶）是一种高效且普适的网络嵌入方法，适用于稠密与稀疏网络场景。

3、引文网络

在两项有向引文网络上的实验结果显示，由于GF和LINE（基于一阶邻近性）方法不适用于有向网络，因此仅比较DeepWalk与LINE（二阶）。通过多标签分类任务评估顶点嵌入效果，选取AAAI、CIKM、ICML、KDD、NIPS、SIGIR和WWW这7个顶级会议作为分类类别。若作者在这些会议发表论文或其论文被收录，则视为属于对应类别。

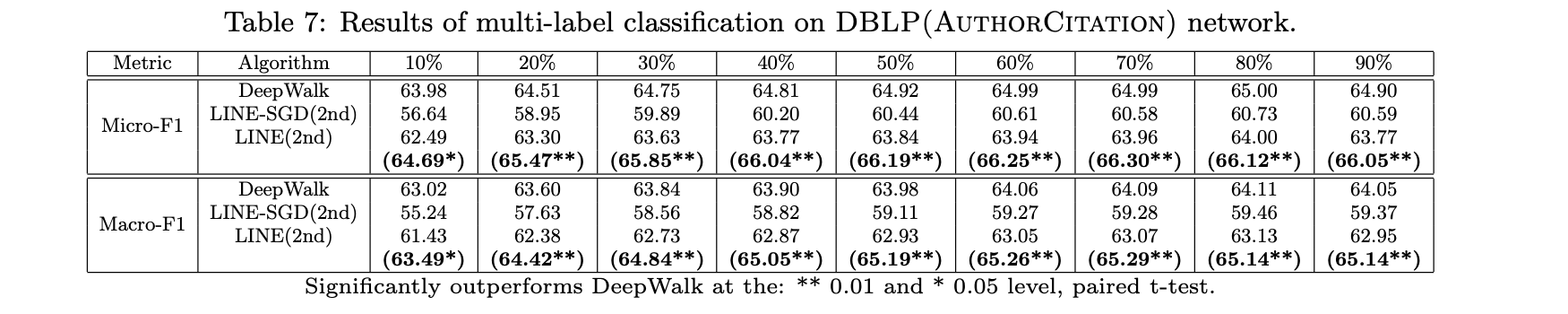
1、DBLP（作者引文）网络

表7展示了DBLP作者引文网络的结果。该网络稀疏性较高，DeepWalk表现优于LINE（二阶）。但通过对低度数节点（度数小于500）递归添加邻居节点重构网络后，LINE（二阶）性能显著提升并反超DeepWalk。采用随机梯度下降直接优化的LINE（二阶）模型未达预期效果。

2、DBLP（论文引文）网络

表8显示，在论文引文网络中，LINE（二阶）显著优于DeepWalk。原因在于随机游走仅能沿引用路径到达较早论文，无法覆盖其他参考文献，而LINE（二阶）通过参考文献表征论文更合理。当对低度数节点（度数小于200）扩充邻居重构网络后，LINE（二阶）性能进一步提升。

3、网络布局

网络嵌入的一个重要应用是生成有意义的可视化效果，将网络布局在二维空间中。该研究从DBLP数据中提取了合著者网络进行可视化，选取了来自三个不同研究领域的会议：数据挖掘领域的WWW、KDD，机器学习领域的NIPS、ICML，以及计算机视觉领域的CVPR、ICCV。合著者网络基于这些会议发表的论文构建，并过滤掉度数小于3的作者，最终网络包含18,561名作者和207,074条边。

由于这三个研究领域彼此紧密关联，布局该合著者网络具有较高挑战性。研究首先通过不同嵌入方法将网络映射到低维空间，随后利用t-SNE工具包将节点的低维向量进一步映射到二维空间。图2对比了不同嵌入方法的可视化结果：基于图分解的布局效果较差，同一社区的作者未能有效聚集；DeepWalk的结果更优，但许多来自不同社区的高度数节点紧密聚集在中心区域。这是因为DeepWalk基于随机游走扩充节点邻居，随机性引入了较多噪声（尤其对高度数节点）。而LINE（二阶）表现优异，生成了更合理的网络布局（同色节点分布更紧密）。

4、网络稀疏性对性能的影响

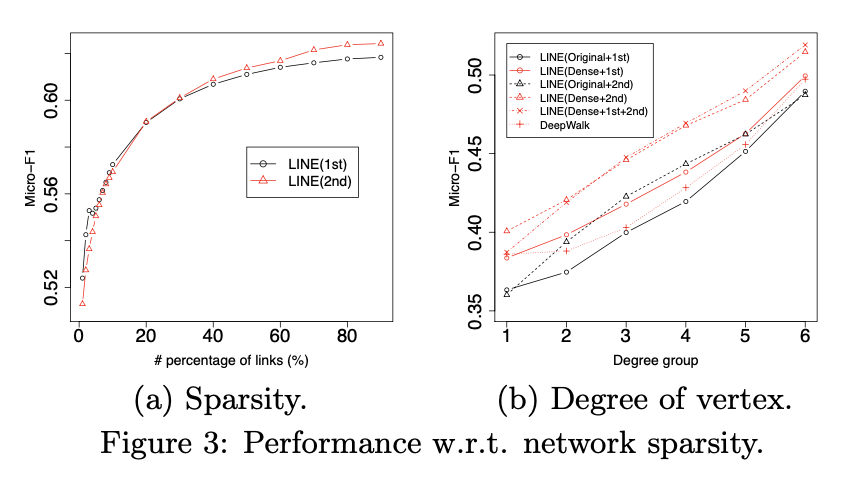
本节以社交网络为例，定量分析上述模型在不同稀疏度网络中的表现。首先探究网络稀疏性对LINE（一阶）和LINE（二阶）的影响。图3(a)展示了Flickr网络（因其比Youtube网络稠密）上模型性能随链接比例变化的实验结果。通过随机选取原始网络中不同比例的链接构造不同稀疏度的子网络，结果显示：当网络极稀疏时，LINE（一阶）优于LINE（二阶）；随着链接比例逐渐增加，LINE（二阶）开始反超。这表明二阶相似性在极端稀疏网络中表现受限，而节点邻域信息充足时其优势显现。

图3(b)对比了原始Youtube网络与重构稠密网络上顶点度数对模型性能的影响。将顶点按度数分组（(0,1]、[2,3]、[4,6]、[7,12]、[13,30]、[31,+∞)）后发现：整体上，模型性能随顶点度数增加而提升。原始网络中，除最低度数组外，LINE（二阶）均优于LINE（一阶），再次验证二阶相似性对低度数节点效果不佳；重构稠密网络中，两种模型性能均提升，其中保留二阶相似性的LINE（二阶）改善尤为显著。值得注意的是，重构网络上LINE（二阶）在所有度数组中均超越DeepWalk。

5、参数敏感性

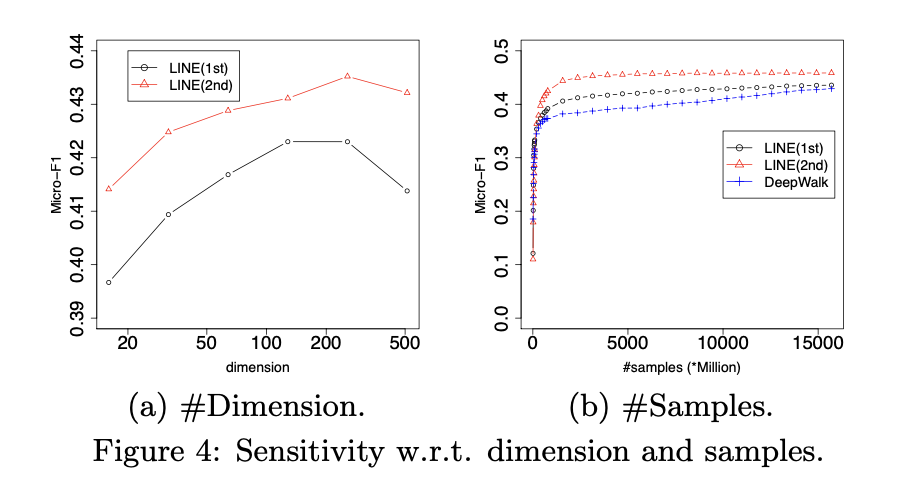
接下来，我们研究参数维度d对性能的影响，以及不同模型在重建的Youtube网络上随样本数量变化的收敛表现。图4(a)展示了LINE模型在不同维度d下的性能表现，可以看出当维度过大时，LINE（一阶）或LINE（二阶）的性能均会下降。图4(b)对比了LINE和DeepWalk在优化过程中随样本数量增加的结果，LINE（二阶）始终优于LINE（一阶）和DeepWalk，且两种LINE模型的收敛速度均显著快于DeepWalk。

6、扩展性

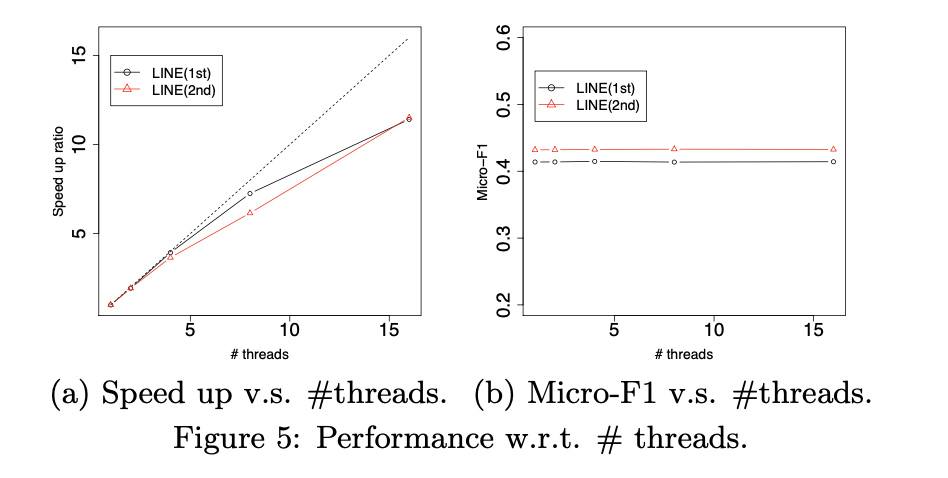
通过边缘采样处理和异步随机梯度下降优化的LINE模型部署了多线程优化，其可扩展性得到了验证。图5(a)展示了在Youtube数据集上线程数量与加速比的关系，加速效果接近线性增长。图5(b)表明，使用多线程更新模型时分类性能保持稳定。两图共同证明，LINE模型的推断算法具有出色的可扩展性。

关键要点

线程加速比：多线程优化下，计算速度随线程数增加呈近线性提升。
性能稳定性：多线程模型更新未对分类任务的准确性产生负面影响。
算法优势：异步梯度下降与边缘采样结合，确保了高效且稳定的分布式计算能力。

二、总结

本文提出了一种名为“LINE”的新型网络嵌入模型，能够轻松扩展到具有数百万个顶点和数十亿条边的大规模网络。该模型精心设计了目标函数，同时保留一阶邻近性和二阶邻近性，二者互为补充。针对模型推断，提出了一种高效且有效的边采样方法，解决了随机梯度下降在加权边上的局限性，同时未影响计算效率。在多个真实网络上的实验结果验证了LINE的高效性和有效性。未来计划研究超越一阶和二阶邻近性的高阶网络邻近性，并探索异构信息网络（如包含多类型顶点的网络）的嵌入方法。

关键术语说明

网络嵌入（Network Embedding）：将网络节点映射到低维向量空间的技术。
一阶邻近性（First-order Proximity）：直接相连节点间的局部相似性。
二阶邻近性（Second-order Proximity）：共享邻居节点的全局相似性。
异构信息网络（Heterogeneous Information Network）：包含多种类型节点或边的网络。

好了，各位到这里，line这偏论文就描述完毕，有问题欢迎评论区随时留言。

查看全文

http://www.xdnf.cn/news/18469.html