人工智能中的(特征选择)数据过滤方法和包裹方法

在人工智能（AI）和机器学习中，“数据过滤方法”和“包裹方法”是两种常见的特征选择技术，用于提高模型性能、减少计算成本，并增强模型的可解释性。下面我来详细解释一下它们的含义和区别：

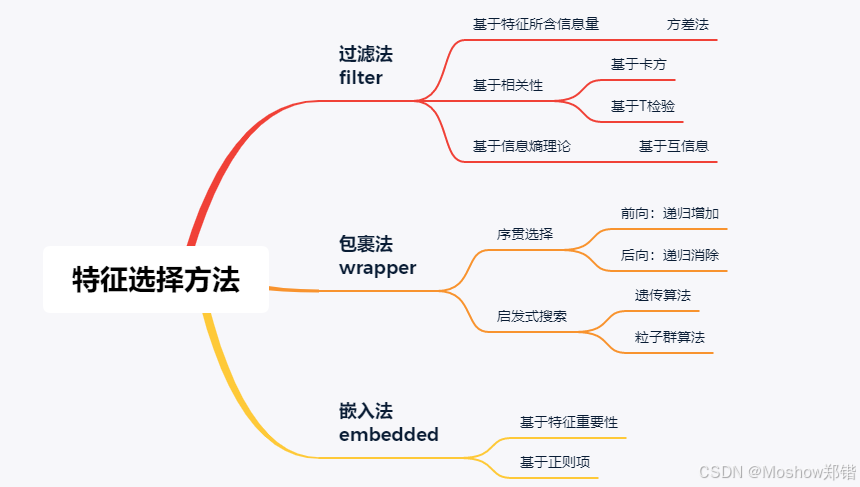
🧹 数据过滤方法（Filter Methods）

定义：在建模之前，独立地评估每个特征与目标变量之间的关系，选择最相关的特征。

特点：

• 与模型无关（模型不可知）

• 快速、计算效率高

• 适用于高维数据（如文本或基因数据）

常见方法：

• 方差阈值（Variance Threshold）：去除方差过低的特征

• 相关系数（如皮尔逊相关）：选择与目标变量相关性高的特征

• 卡方检验（Chi-square test）：用于分类任务

• 信息增益（Information Gain）：用于评估特征对目标变量的信息贡献

优点：

• 简单快速

• 不依赖具体模型

• 可用于预处理阶段

缺点：

• 忽略特征之间的交互

• 可能选出对模型实际效果不佳的特征

🎁 包裹方法（Wrapper Methods）

定义：将特征选择过程与模型训练结合起来，通过评估模型在不同特征子集上的表现来选择最佳特征组合。

特点：

• 与模型紧密结合

• 计算成本高

• 更能捕捉特征之间的相互作用

常见方法：

• 递归特征消除（RFE, Recursive Feature Elimination）

• 前向选择（Forward Selection）

• 后向消除（Backward Elimination）

• 穷举搜索（Exhaustive Search）

优点：

• 考虑特征之间的组合效果

• 通常能得到更优的特征子集

缺点：

• 计算代价高，尤其在特征维度高时

• 可能容易过拟合

🧠 举个例子来理解

假设你在做一个预测学生考试成绩的模型：

• 过滤方法可能会告诉你“学习时间”和“睡眠时间”与成绩高度相关，因此你保留它们。

• 包裹方法则会尝试不同的特征组合，比如“学习时间 + 上课出勤率”或“睡眠时间 + 饮食习惯”，然后看哪组特征让模型表现最好。