COAT: 压缩优化器状态和激活以实现内存高效的FP8训练

温馨提示：
本篇文章已同步至"AI专题精讲" COAT: 压缩优化器状态和激活以实现内存高效的FP8训练

摘要

FP8训练已成为提高训练效率的一个有前景的方法。现有的框架通过将FP8计算应用于线性层，同时将优化器状态和激活保持在更高精度，从而加速训练，但未能充分优化内存使用。本论文介绍了COAT（压缩优化器状态和激活以实现FP8训练），这是一种新型的FP8训练框架，旨在显著减少训练大规模模型时的内存占用。COAT通过两项关键创新解决了现有方法的局限性：（1）动态范围扩展，能够使优化器状态的分布更接近FP8表示范围，从而减少量化误差；（2）混合粒度激活量化，通过结合按张量和按组量化策略来优化激活内存。实验表明，COAT与BF16相比，有效地将端到端训练的内存占用减少了1.54倍，同时在各种任务（如大规模语言模型的预训练与微调、视觉语言模型训练）上实现了几乎无损的性能。与BF16相比，COAT还实现了1.43倍的端到端训练加速，性能与TransformerEngine的加速效果相当或更好。COAT使得在较少的GPU上高效地进行大模型的全参数训练，并有助于在分布式训练设置中将批量大小翻倍，为大规模模型训练的扩展提供了实际的解决方案。代码可在 https://github.com/NVlabs/COAT 获取。

1 引言

基础模型（FMs），如大规模语言模型（LLM）和视觉语言模型（VLM），在推理、理解和总结等多个任务上取得了显著突破（Dubey等，2024；Adler等，2024；Team等，2024；Lin等，2024）。然而，这些模型通常包含数十亿个参数，它们的训练需要大量的计算资源和内存。这带来了巨大的挑战，使得训练这些基础模型变得非常困难（Smith等，2022；Hoffmann等，2022）。

低精度训练已成为一种有前景的方法，可以使基础模型的训练更加高效（Micikevicius等，2017；Wang等，2018；Zhu等，2020；Xi等，2023；Wortsman等，2023；Xi等，2024）。通过将深度神经网络中使用的张量量化为较低的精度，低精度训练能够有效地加速训练过程并减少内存占用。目前，BF16训练（Kalamkar等，2019；Micikevicius等，2017）是最常见的低精度方法，并已广泛应用于大规模训练框架，如DeepSpeed（Rasley等，2020）和Megatron-LM（Shoeybi等，2019）。

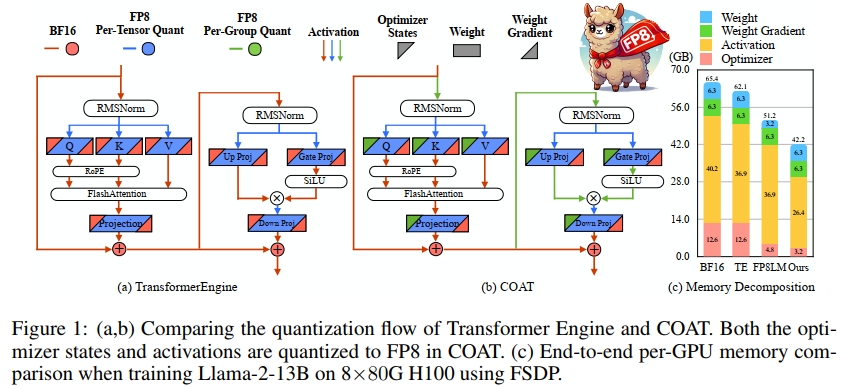
随着Nvidia H100 GPU（NVIDIA，2024a）的问世，FP8训练（Micikevicius等，2022）作为下一代低精度技术开始崭露头角。与BF16相比，FP8训练有潜力（1）将速度翻倍，（2）将内存占用减半。为了实现实际的加速，Transformer Engine（NVIDIA，2024b）采用FP8精度执行矩阵乘法，从而加快训练速度。通过将优化器状态、梯度、权重和激活量化为较低精度，Transformer Engine的内存占用可以进一步优化。如图1所示，FP8-LM（Peng等，2023）通过进一步将梯度、权重主副本和一阶动量量化为FP8，从而减少了内存和通信开销，部分提高了内存效率。然而，它们未能解决激活的内存消耗问题，且仍然将优化器的二阶动量保留在较高精度中。当优化器、梯度和权重在多个GPU上通过ZeRO或FSDP进行分片时，激活的内存问题变得更加严重。此外，二阶动量比一阶动量对量化更为敏感（Fishman等，2024），而激活的波动性大也使得它们难以量化为FP8（Yang等，2024）。这种潜在的精度下降使得它们错失了进一步优化内存的关键机会。

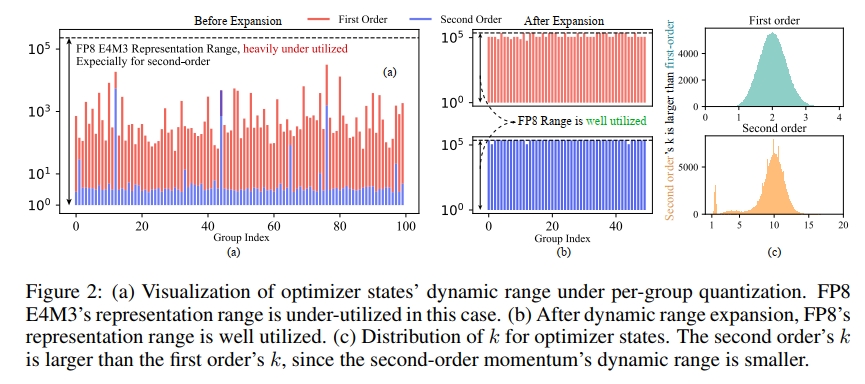
在这项工作中，我们提出了COAT：压缩优化器状态和激活以实现内存高效的FP8训练，来解决上述问题。COAT通过将优化器状态和激活量化为FP8，大幅减少了整体内存占用。对于优化器状态，我们观察到，当对其进行量化时，FP8格式的表示范围未被充分利用，如图2(a)所示。为了解决这一问题，我们提出了一种新颖的动态范围扩展方法，调整优化器状态的分布，使其更好地适应FP8范围，从而最小化量化误差。对于激活，我们提出了混合粒度激活量化，以实现高效且精确的量化。我们对非线性层应用细粒度量化，对线性层应用按张量量化。矩阵乘法的按张量量化更加高效，且更适合TensorCores，而细粒度量化有助于保持精度。这两种方法解决了高内存消耗的问题，同时确保了最小的性能下降。图1(b)展示了COAT的概览。

我们在广泛的任务上展示了COAT的准确性能，包括LLM预训练、LLM微调和VLM训练。COAT在所有这些任务上都实现了几乎无损的性能。在效率方面，COAT相比BF16实现了1.54倍的端到端内存减少，并在Llama 7B、13B和30B模型上实现了1.43倍的端到端训练加速。此外，COAT还在所有现实的分布式训练设置中将批量大小翻倍，这对于更高的加速和支持更长的上下文长度至关重要，从而使大规模模型的训练过程更加高效。

2 相关工作

低精度训练
低精度训练（Wang等，2018；Chen等，2020；Lin等，2022；Wortsman等，2023；Xi等，2024）已成为现代深度学习中的一项重要技术，能够在降低计算成本和内存需求的同时提高效率。FP16（半精度）训练（Micikevicius等，2017）是当前最为普遍的低精度方法。FP16训练通过引入损失缩放来解决其较窄表示范围的问题。BF16训练（Kalamkar等，2019）在此基础上进行了改进，因为BF16具有更大的表示范围，并且在大规模训练中更加稳定。在这些方法中，前向和反向传播操作使用FP16或BF16精度进行计算，而主权重、梯度和优化器状态则保留在FP32精度下。

FP8训练
FP8训练（Fishman等，2024；Micikevicius等，2022）旨在进一步提升这些效率提升。随着Nvidia Hopper GPU架构的问世，FP8正成为下一代低精度训练的实用数据类型。Nvidia的Transformer Engine（TE）（NVIDIA，2024b）是第一个为FP8混合精度训练设计的框架，采用FP8 Tensorcore进行线性层的计算。FP8-LM（Peng等，2023）将FP8量化扩展到梯度和优化器状态，进一步提升了训练吞吐量。然而，它们未能减少用于反向传播存储的激活的内存使用（使用FP8），并且仍然将二阶动量保留在FP16中，从而限制了FP8内存优势的完全发挥。

内存高效优化器
虽然32位优化器（Kingma，2014；Loshchilov，2017）状态被广泛采用，但已有多项研究致力于通过量化减少优化器状态的内存占用。8位Adam（Dettmers等，2021）引入了一种名为动态指数（DE）的新型数据格式进行量化，但该新数据格式的采用限制了其灵活性。4位优化器（Li等，2024）进一步将优化器量化推至4位，并通过解决零点问题，但仅限于微调任务。FP8-LM（Peng等，2023）将一阶动量量化为FP8，同时将二阶动量保留在FP16中，限制了整体内存节省。（Fishman等，2024）发现二阶动量对量化更加敏感，并提出使用E5M2格式对其进行量化。

除了量化之外，还有其他方法旨在减少优化器状态的内存占用（Shazeer & Stern，2018；Anil等，2019；Chen等，2024；Zhao等，2024），例如低秩分解和优化器简化，只存储一阶动量。这些方法与我们的方法是正交的。

激活量化
近期的研究集中在通过激活量化减少神经网络训练的内存占用（Cai等，2020）。ActNN（Chen等，2021）提出了一种2位激活压缩训练框架，采用随机量化，实现了激活内存占用的12倍减少。GACT（Liu等，2022a）扩展了这一概念，支持各种机器学习任务和架构，为CNN、Transformer和GNN提供了最高8.1倍的激活内存减少。然而，这些方法主要集中在卷积网络上，不适用于LLM。AQ-SGD（Wang等，2022）提出压缩激活变化而不是直接的值，用于管道并行训练，以减少管道并行设置中的通信开销。Few-Bit Backward（Novikov等，2023）通过使用最优的分段常数逼近对非线性激活函数进行量化，以减少内存占用并保持收敛性。Jetfire（Xi等，2024）提出INT8数据流，将线性层和非线性层的激活量化为INT8，以减少内存占用，并且适用于语言模型的预训练。

比特宽度下利用平衡量化
Zhou等（2017）通过百分位递归划分参数，以减少量化误差。DDSQ（Wang & Kang，2023）根据不同的梯度分布动态调整量化参数。N2UQ（Liu等，2022b）通过学习输入阈值和非均匀映射来改善量化精度。这些方法都意识到量化中的动态范围问题，并提出了更具适应性、分布感知的技术，能够保留全精度中的细微信息。它们共享的基本目标是扩展低精度神经网络表示的有效动态范围。这些方法采用可学习的非均匀量化查找表，而我们的工作依赖于自然的FP8数据格式。

3 预备知识

FP8量化
量化通过将高精度张量压缩为低精度，从而实现加速和节省内存占用，但代价是精度降低和表示范围变小。FP8格式由两种编码方式组成——E4M3和E5M2（Open Compute Project，2023）。E4M3具有更高的精度，而E5M2则具有更大的表示范围。我们定义E4M3的最小值和最大值为 ${\Delta }_{\min }^{E4M3}=2^{-9}$ 和 ${\Delta }_{\max }^{E4M3}=448$，而E5M2的最小值和最大值分别为${\Delta }_{\min }^{E5M2}=2^{-16}$和 ${\Delta }_{\min }^{E5M2}=57344$。

为了将一个FP32张量 X 量化为E4M3精度，我们使用一个量化器 Q(·) 将该张量映射到FP8的表示范围内。这个过程可以表示为：
$$X_{FP8},S_X=Q(X_{FP32}),\mathrm{where}{X}_{FP8}=\lceil \frac{X_{FP32}}{S_X}\rceil ,S_X=\frac{\max \left(|X_{FP32}|\right)}{{\Delta }_{\max }^{E4M3}}$$
其中，$S_X$ 是缩放因子，$\lceil \cdot \rfloor$ 表示四舍五入到最近值。量化为E5M2遵循类似的过程，我们只需将 ${\Delta }_{\max }^{E4M3}$ 替换为 ${\Delta }_{\max }^{E5M2}$。为了将量化后的张量映射回FP32精度，反量化操作 $DQ(\cdot )$ 可以表示为：

$$X_{\text{FP32}}=DQ(X_{\text{FP8}},S_X)=S_X\cdot X_{\text{FP8}}$$

优化器更新规则
优化器在深度学习中被广泛使用以更新参数。最常见的基于梯度的优化器是 Adam/AdamW（Kingma，2014；Loshchilov，2017），它使用一阶动量 $m$ 和二阶动量 $v$ 来实现更好的收敛。AdamW 在时间步 $t$ 的更新规则可以表示为：
$$\begin{array}{rl}& m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_{t-1}{v}_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_{t-1}^2\\ & {\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}{\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}\\ & w_{t+1}=w_t-\eta \left(\frac{{\hat{m}}_t}{\sqrt{{\hat{v}}_t}+ϵ}+\lambda w_t\right)\end{array}(1)$$
其中，$m_t$ 是一阶动量，$v_t$ 是二阶动量，$g_t$ 是梯度，${\beta }_1$ 和 ${\beta }_2$ 是 AdamW 的动量系数，$\eta$ 是学习率，$\lambda$ 是权重衰减，$ϵ$ 用于防止出现 NaN 或 Inf。

为了对优化器状态进行量化，我们对一阶动量和二阶动量均采用分组量化，遵循以往工作（Dettmers 等，2021；Li 等，2024）。每连续 $G$ 个元素组成一个组（$G$ 为组大小），每个组根据自身统计信息独立量化。优化器状态以 FP8 精度存储，其缩放因子存储为 BF16。在 FSDP 或 ZeRO-3 中，优化器状态相关的统计信息（如缩放因子）不会在 GPU 之间同步，因为每个 GPU 维护其各自的优化器状态分片。更多细节见附录 A。

4 动态范围扩展以实现准确的优化器量化

在接下来的章节中，我们将解释COAT如何利用FP8量化实现内存高效的FP8训练，同时不损失精度。第4节聚焦于优化器状态的量化，第5节讨论激活的量化。

4.1 现有优化器状态量化方法存在的问题

在分组量化下，我们发现当前量化方法的一个显著缺点是未能充分利用FP8的表示范围，导致较大的量化误差。以E4M3数据格式为例，E4M3最大可表示值与最小可表示值之比为：

$$\begin{array}{r}{\Delta }_{\max }^{E4M3}/{\Delta }_{\min }^{E4M3}=448÷\frac{1}{512}=229376\approx 2\times 10^5.\end{array}$$
因此，对于一个量化组 $X$，如果我们希望充分利用FP8的256个可表示值，我们希望该量化组的动态范围能够覆盖从 ${\Delta }_{\min }^{E4M3}$ 到 ${\Delta }_{\max }^{E4M3}$ 的整个区间。

更正式地，我们将动态范围定义为量化组 $X$ 内最大绝对值与最小绝对值的比值：

定义1（动态范围）
给定一个包含 $G$ 个实数的集合 X={x1,x2,…,xG}X = \{x_1, x_2, \ldots, x_G\}X={x1​,x2​,…,xG​}，动态范围 $R$ 定义为：
$${\mathcal{R}}_X=\frac{\max (|x_1|,|x_2|,\dots ,|x_G|)}{\min (|x_1|,|x_2|,\dots ,|x_G|)}$$
其中，$|\cdot |$ 表示绝对值。

也就是说，E4M3的动态范围为 $R_{E4M3}=448\times 512=229376\approx 2\times 10^5$。然而，实际上，优化器状态中的许多量化组未能有效地将数值映射到如此宽广的范围内。我们观察到，优化器状态高度稀疏，只有不到1%的数值具有较大幅度，而大多数数值较小且集中在一起。由于大数值极少，大多数组的动态范围较低。如图2(a)所示，一阶动量的动态范围通常小于 $1\mathrm{e}4,$，二阶动量的动态范围通常小于 $1\mathrm{e}1,$这两者都远低于FP8的可用范围。因此，FP8的表示能力有很大一部分被浪费，导致较大的量化误差。

4.2 动态范围扩展

为了解决上述问题，我们在量化之前引入一个扩展函数 $f(\cdot )$ 来扩展量化组的动态范围，使其与 E4M3 的动态范围对齐，该过程可形式化为：

$$X_{FP8},S_X=Q(f(X_{FP32}))$$

我们所使用的扩展函数定义为：

$$f(x)=\text{sign}(x)\times |x{|}^k$$

其中，$k$ 用于控制扩展的强度。在附录中，我们证明了该方法是最优的。对于量化组 $X$，应用扩展函数 $f$ 后，其动态范围变为：

$${\mathcal{R}}_{f(X)}=\frac{\max (|f(X)|)}{\min (|f(X)|)}=\frac{\max (|\mathrm{sign}(X)X^k|)}{\min (|\mathrm{sign}(X)X^k|)}=(\frac{\max (|X|)}{\min (|X|)}{)}^k=({\mathcal{R}}_X{)}^k.$$

因此，当 $k>1$ 时，动态范围 ${\mathcal{R}}_X$ 会被放大，更接近理想的 ${\mathcal{R}}_{E4M3}$。最优的 $k$ 满足：

$$({\mathcal{R}}_X{)}^k={\mathcal{R}}_{E4M3}⟹k={\log }_{{\mathcal{R}}_X}({\mathcal{R}}_{E4M3})$$

使用该最优的 $k$，函数 $f(X)$ 可以充分利用 E4M3 的表示范围，而原始的 $X$ 只能利用其一小部分。如图2©所示，二阶动量通常具有较大的 $k$ 值（约在5到15之间），而一阶动量的 $k$ 值较小（约在1到3之间）。这对应了我们之前的观察，即二阶动量的动态范围通常比一阶动量小，因此需要更大的 $k$ 来更好地对齐 E4M3 的动态范围。

为了保证准确性，我们在每个优化器步骤中，对每个量化组实时计算 $k$。在反量化时，我们应用扩展函数的逆函数：

$$f^{-1}(x)=x^{\frac{1}{k}}$$

来恢复其原始值，表达式为：

$$X^{FP32}=f^{-1}(DQ(X_{FP8},S_X))$$

我们将常规量化器和动态范围扩展方法分别应用于一阶动量 $m$ 和二阶动量 $v$。如图2(b)所示，扩展后的分布能够充分利用 FP8（E4M3）的表示范围，验证了我们方法的有效性。我们在表格中进一步量化了该方法的效果。

在 AdamW 优化步骤中，如公式中所述，$\frac{m}{\sqrt{v}+ϵ}$ 是实际用于权重更新的有效项，因此我们报告 $\frac{m}{\sqrt{v}+ϵ}$ 的均方误差（MSE）来量化量化方法的性能。我们发现 E4M3 比 E5M2 更适合一阶动量。对于二阶动量，虽然 E4M3 也优于 E5M2，但在应用我们的扩展函数后，它们的量化误差几乎相同。我们的动态范围扩展方法可以将 MSE 有效降低约 1.63 倍。更多结果见附录 A。

温馨提示：
阅读全文请访问"AI深语解构" COAT: 压缩优化器状态和激活以实现内存高效的FP8训练