cuda编程笔记(9)--使用 Shared Memory 实现 tiled GEMM
tiled GEMM 是在 GPU 上使用 共享内存(Shared Memory)优化通用矩阵乘法(GEMM, General Matrix Multiply) 的一种经典方法,其核心思想是 将大矩阵拆分为更小的 tile(子块),再通过共享内存提高缓存命中率和并行计算效率。
任务:给定矩阵 A(M×K),B(K×N),计算 C = A × B,得到矩阵 C(M×N)
使用 tile(块) 的思想:
-
把矩阵分成小块(如 16×16),一块块加载进共享内存;
-
让每个线程处理一个 C[i][j] 元素;
-
每次只加载 A 和 B 的一块(tile),乘积累加进 C 的对应值;
-
这样能显著减少对 global memory 的慢速访问。
先给出代码,再详细讲解
#ifndef __CUDACC__
#define __CUDACC__
#endif
#include <cuda_runtime.h>
#include <device_launch_parameters.h>#include <iostream>
#include<cstdio>#define TILE_SIZE 16
void error_handling(cudaError_t res) {if (res !=cudaSuccess) {std::cout << "error!" << std::endl;}
}
__global__ void tiledGEMM(float* A, float* B, float* C, int M, int N, int K) {//一个block里有TILE_SIZE*TILE_SIZE个线程__shared__ float tileA[TILE_SIZE][TILE_SIZE];__shared__ float tileB[TILE_SIZE][TILE_SIZE];//当前线程负责的C矩阵中的行和列//为什么这么算,TILE_SIZE说成blcokDim.y更直观,因为两者是相等的int row = blockIdx.y * TILE_SIZE + threadIdx.y;int col = blockIdx.x * TILE_SIZE + threadIdx.x;float temp = 0;//每个block内,把对应区域的A和B矩阵填入tileA和tileBfor (int t = 0; t < (K + TILE_SIZE - 1) / TILE_SIZE; t++) {if (row < M && t * TILE_SIZE + threadIdx.x < K)tileA[threadIdx.y][threadIdx.x] = A[row * K + t * TILE_SIZE + threadIdx.x];elsetileA[threadIdx.y][threadIdx.x] = 0;// 从全局内存拷贝 B 的 tile 到共享内存(小心边界)if (t * TILE_SIZE + threadIdx.y < K && col < N)tileB[threadIdx.y][threadIdx.x] = B[(t * TILE_SIZE + threadIdx.y) * N + col];elsetileB[threadIdx.y][threadIdx.x] = 0;// 等待所有线程把 tile 加载进来__syncthreads();// 每个线程负责 tile 的一行和一列相乘求和for (int k = 0; k < TILE_SIZE; ++k)temp += tileA[threadIdx.y][k] * tileB[k][threadIdx.x];// 所有线程同步,准备下一轮 tile 加载__syncthreads();}// 将结果写回 C(小心越界)if (row < M && col < N)C[row * N + col] = temp;
}int main() {const int M = 64;const int K = 64;const int N = 64;size_t bytesA = M * K * sizeof(float);size_t bytesB = K * N * sizeof(float);size_t bytesC = M * N * sizeof(float);float* h_A = new float[M * K];float* h_B = new float[K * N];float* h_C = new float[M * N];// 初始化 A 和 Bfor (int i = 0; i < M * K; ++i) h_A[i] = 1.0f;for (int i = 0; i < K * N; ++i) h_B[i] = 1.0f;float* d_A, * d_B, * d_C;cudaMalloc(&d_A, bytesA);cudaMalloc(&d_B, bytesB);cudaMalloc(&d_C, bytesC);cudaMemcpy(d_A, h_A, bytesA, cudaMemcpyHostToDevice);cudaMemcpy(d_B, h_B, bytesB, cudaMemcpyHostToDevice);// 设置 Grid 和 Blockdim3 blockDim(TILE_SIZE, TILE_SIZE);dim3 gridDim((N + TILE_SIZE - 1) / TILE_SIZE,(M + TILE_SIZE - 1) / TILE_SIZE);// 调用 kerneltiledGEMM << <gridDim, blockDim >> > (d_A, d_B, d_C, M, N, K);cudaDeviceSynchronize();// 拷贝结果回主机cudaMemcpy(h_C, d_C, bytesC, cudaMemcpyDeviceToHost);// 简单输出前 10 个值检查for (int i = 0; i < 10; ++i)std::cout << h_C[i] << " ";std::cout << std::endl;// 清理内存delete[] h_A;delete[] h_B;delete[] h_C;cudaFree(d_A);cudaFree(d_B);cudaFree(d_C);return 0;
}在本例子中,BlockDim.x=BlockDim.y=TILE_SIZE
- 因为矩阵C的规模是(M×N)所以总共的线程是也是(M×N)个;
- 每个Block负责矩阵C中一块(BlockDim.x × BlockDim.y)也即(TILE_SIZE × TILE_SIZE)大小的区域;
- 而Block中的每个线程负责C[i][j],也即矩阵C的单独一个位置的值的计算
矩阵C中C[i][j]的计算公式为:
由于每次只能将(TILE_SIZE × TILE_SIZE)大小的矩阵加载进共享内存,而一块(TILE_SIZE × TILE_SIZE)大小的矩阵A区域和一块(TILE_SIZE × TILE_SIZE)大小的矩阵B区域,不一定能够完成C[i][j]的计算
见下图:
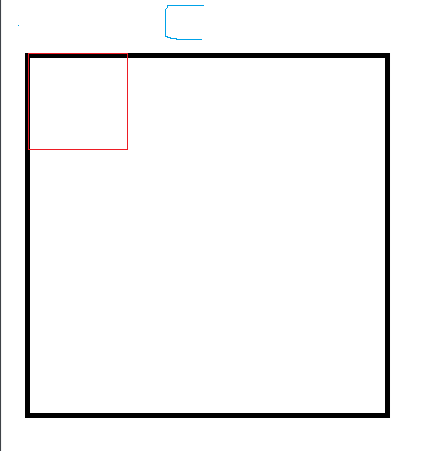
红色区域是本Block负责的(TILE_SIZE × TILE_SIZE)的区域,而计算这些区域C矩阵的值需要用到如下A,B矩阵的区域
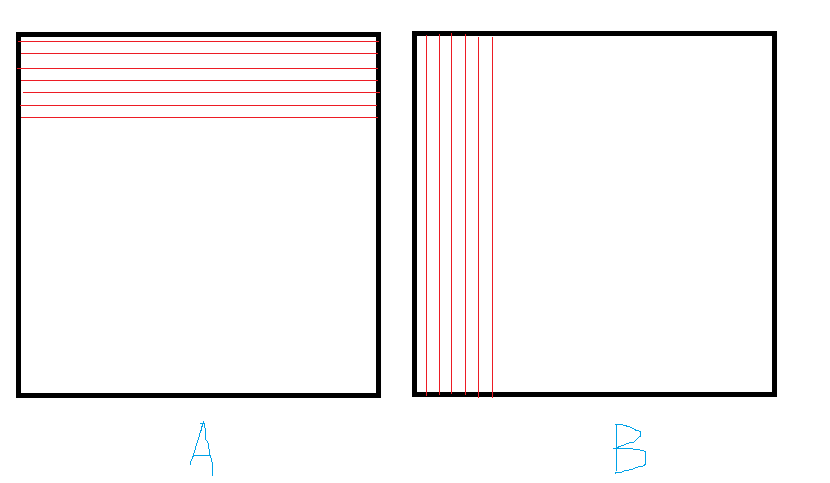
可是Block内的共享矩阵大小也是 (TILE_SIZE × TILE_SIZE)的,我们只能每次框住对应大小,并且不停迭代来进行移动
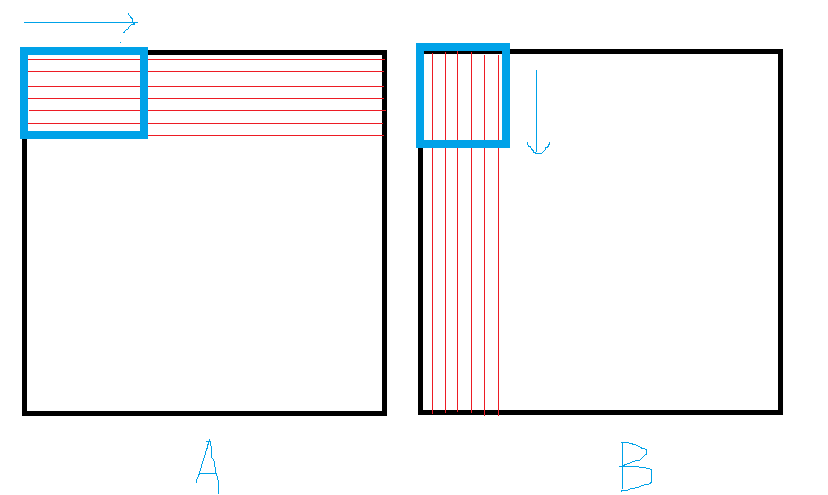
我们来逐句解释tiledGEMM核函数:
__shared__ float tileA[TILE_SIZE][TILE_SIZE];__shared__ float tileB[TILE_SIZE][TILE_SIZE];这是每个Block内共享的小块矩阵,对应的即使图3中蓝色框圈住的A、B的区域
//TILE_SIZE说成blcokDim.y更直观,因为两者是相等的int row = blockIdx.y * TILE_SIZE + threadIdx.y;int col = blockIdx.x * TILE_SIZE + threadIdx.x;这是计算本线程负责的C[row][col]的位置,计算原理在CUDA编程笔记(1)--最简单的核函数-CSDN博客中获取线程全局 ID小节有讲过,请自行学习
float temp = 0;对于每个C[row][col],不能一次性算出它的值,得经过多次累加,所以需要声明一个变量进行存储
for (int t = 0; t < (K + TILE_SIZE - 1) / TILE_SIZE; t++) {}整个for循环,参考图3的情况,即是蓝色框进行移动,每次迭代,蓝色框就向对应方向进行移动
for循环内部:
if (row < M && t * TILE_SIZE + threadIdx.x < K)tileA[threadIdx.y][threadIdx.x] = A[row * K + t * TILE_SIZE + threadIdx.x];elsetileA[threadIdx.y][threadIdx.x] = 0;// 从全局内存拷贝 B 的 tile 到共享内存(小心边界)if (t * TILE_SIZE + threadIdx.y < K && col < N)tileB[threadIdx.y][threadIdx.x] = B[(t * TILE_SIZE + threadIdx.y) * N + col];elsetileB[threadIdx.y][threadIdx.x] = 0;这些代码的作用就是把蓝色框内的A、B矩阵是数据转移到共享内存tileA,tileB中。A,B是将逻辑上的二维矩阵转为实际存储的一维数组;其中A[],B[]的下标计算即是按照行/列优先的方式来计算的,这里不懂的去自行复习一下矩阵下标的计算;
__syncthreads();第一个__syncthreads();是等待所有线程都把当前蓝色框的内容转移到tileA和tileB中
for (int k = 0; k < TILE_SIZE; ++k)temp += tileA[threadIdx.y][k] * tileB[k][threadIdx.x];一个C[row][col]对应A的一长行和B的一长列,但是一次tileA和tileB只能加载一部分,只能先把tileA和tileB里面的对应部分相乘加起来存起来
__syncthreads();所有线程同步,准备下一轮 tile 加载
dim3 blockDim(TILE_SIZE, TILE_SIZE);
dim3 gridDim((N + TILE_SIZE - 1) / TILE_SIZE,(M + TILE_SIZE - 1) / TILE_SIZE);这里blockDim和gridDim总乘积为M*N(M、N为TILE_SIZE倍数的情况下),刚好每个线程对应矩阵C的一个元素
