【推理的思想】程序正确性证明（一）：演绎推理基础知识

要判定被测对象的正确性，最直接的手段，就是枚举测试，而且要用完整的原始期望做测试准绳。可问题是，即便我们贯彻了枚举的思想，做的是“聪明的枚举”，成本仍然可能会很高。这时候，推理的思想就能帮助我们，进一步控制正确性判定的成本。

一种典型的做法就是通过演绎推理，来证明程序是正确的，或者在某些方面是正确的。提到演绎推理，我们首先想到的是这位老兄：

《血字的研究》这个篇章中，福尔摩斯跟华生说过这样一段话：“在平淡无奇的生活纠葛里，谋杀案就像一条红线一样，贯穿在中间。我们的责任就是要去揭露它，把它从生活中清理出来，彻底地加以暴露。”

这条红线，就是从“前提”到“结论”的演绎推论过程。在测试设计的世界里，我们希望这条线最终指向的结论是——被测对象是正确的。把前提和结论连接起来的，是推理规则。推理规则是演绎推理的逻辑核心。

命题逻辑里，常用的推理规则包括以下13条：

(1) 前提引入规则：在演绎推理的过程中，可以随时引入已知的前提，比如各种公理；

(2) 结论引入规则：在演绎的任何步骤上得到的结论，都可以当做后续演绎的前提来用；

(3) 等值置换规则：可以按等值演算规律，对命题公式中的一部分进行替换。命题逻辑中的16组等值演算规律如下：

(4) 假言推理规则：如果A蕴含B成立，且A成立，那么B就成立。形式化表述为：

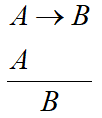
(5) 附加规则：如果A成立，那么A∨B就成立。形式化表述为：

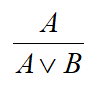
  (6) 化简规则：

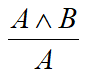
  (7) 拒取式规则：

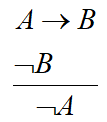
  (8) 假言三段论规则：

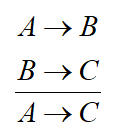
  (9) 析取三段论规则：

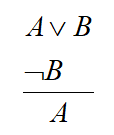
  (10) 构造性二难推理规则：

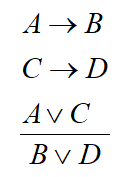
  (11) 破坏性二难推理规则：

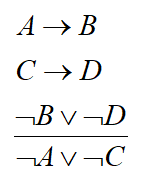
  (12) 合取引入规则：

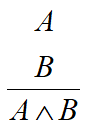
  (13) 归结规则：

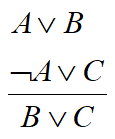
上面13条推理规则，反映的是命题逻辑中的因果规律。实际上，不同的领域有着不同的因果规律，因此也可以定义不同的推理规则。

还有一点值得注意：命题逻辑是有局限性的，有时候会影响演绎推理的进行。我们知道，古希腊有“三贤”，苏格拉底、柏拉图、亚里士多德——老苏、老柏、老亚：

老苏是老柏的师父，老柏是老亚的师父。老亚拿自己的师祖举例子，提出过一个著名的三段论：人都会死（记作命题p），苏格拉底是人（记作命题q），所以苏格拉底会死（记作命题r）。显然这是一个正确的演绎推理过程。但是只靠命题逻辑，我们没办法从前提p和q推导出r这个结论，因为命题逻辑不能反映p、q、r之间的内在关系。

这时候，我们就需要用谓词逻辑。比如“人都会死”这个命题，可以表达成这样一个谓词逻辑公式：，意思是“任意x，如果H(x)成立，则D(x)成立”。其中是量词，x是个体词，H(x)和D(x)是谓词。H(x)指的是x是人，D(x)指的是x会死。

谓词逻辑不仅满足之前提到的16组命题逻辑等值演算规律，还满足这样4组跟量词有关的等值演算规律：

比如量词消去律的第一条，意思就是，任意x都有A(x)成立，等价于命题A在所有个体上都成立。

我们把苏格拉底这个个体记作s，如果（即“人都会死”）这个谓词公式成立，根据量词消去律，可知H(s)→D(s)成立。再引入“苏格拉底是人”这个前提，也就是H(s)成立，根据假言推理规则，就直接得到了D(s)成立，也就是“苏格拉底会死”的结论。