IMU噪声模型

参考来源：
1、deepseek
2、kalibr文档

IMU噪声模型

Kalibr中使用的IMU测量模型包含两种类型的传感器误差：一个快速波动的加性噪声项（“白噪声”）$n$，和一个缓慢变化的传感器偏差（零偏）$b$。角速度测量值$\tilde{\omega }$（以陀螺仪的一个单轴为例）：

$$\tilde{\omega }(t)=\omega (t)+b(t)+n(t)$$

• • 解释: 这是单个陀螺仪轴测量值 $\tilde{\omega }(t)$ 在时间 $t$ 的分解公式。
  • $\omega (t)$: 真实的角速度值。这是我们想要测量的物理量。
  • $b(t)$: 随时间缓慢变化的零偏 (Bias)。它不是常数，而是一个随机过程（后文用随机游走建模）。
  • $n(t)$: 随时间快速波动的加性白噪声 (Additive White Noise)。它是一个零均值、高频的随机过程。
  • 含义: 实际测量值 $\tilde{\omega }(t)$ 等于真实角速度 $\omega (t)$ 加上一个缓慢变化的误差 $b(t)$ 再加上一个快速变化的误差 $n(t)$。
  • 适用范围: 这个模型结构同样独立地应用于加速度计的每个轴（只需将 $\omega$ 替换为加速度 $a$）。每个轴有自己的 ${\sigma }_g,{\sigma }_a,{\sigma }_{b_g},{\sigma }_{b_a}$ 参数。

加性"白噪声"

传感器信号的快速波动用零均值、独立、连续时间的白高斯噪声过程$n(t)$，以其强度为${\sigma }_g$来建模：

$$E[n(t)]\equiv 0$$

$$E[n(t_1)n(t_2)]={\sigma }_g^2\delta (t_1-t_2)$$

换句话说，${\sigma }_g$越高，陀螺仪测量就越"嘈杂"。Kalibr中gyroscope_noise_density和accelerometer_noise_density参数正好指定了这些连续时间模型的噪声强度${\sigma }_g$（陀螺仪）和${\sigma }_a$（加速度计）。

• • 解释: 这两式定义了白噪声 $n(t)$ 的统计行为。
  • $E[n(t)]\equiv 0$: 白噪声的期望（均值）恒为零。这意味着噪声没有系统性偏移，正负波动在长期平均下相互抵消。
  • $E[n(t_1)n(t_2)]={\sigma }_g^2\delta (t_1-t_2)$: 这是白噪声的自相关函数 (Autocorrelation Function)。
    • $\delta (t_1-t_2)$: 狄拉克 δ 函数 (Dirac Delta Function)。它在 $t_1=t_2$ 时为无穷大，在 $t_1\ne t_2$ 时为 0，并且在整个实数轴上的积分为 1。这个函数的关键性质是：${\int }_{-\infty }^{\infty }f(t)\delta (t-\tau )dt=f(\tau )$。
    • 含义: 这个等式说明：
      • 当 $t_1=t_2$ 时，$E[n(t_1)n(t_1)]=E[n^2(t_1)]={\sigma }_g^2$。这表示噪声在 同一时刻 的方差（波动强度）是 ${\sigma }_g^2$。${\sigma }_g$ 就是这个白噪声过程的标准差，称为 “噪声密度 (Noise Density)”。
      • 当 $t_1\ne t_2$ 时，$E[n(t_1)n(t_2)]=0$。这意味着噪声在 不同时刻 的值是完全不相关 (Uncorrelated) 的。白噪声在时间上没有任何记忆性，当前时刻的噪声值对下一时刻的噪声值没有任何影响。
  • 单位: ${\sigma }_g$ 的单位是 $\frac{rad}{s}\frac{1}{\sqrt{Hz}}$ (对于陀螺仪) 或 $\frac{m}{s^2}\frac{1}{\sqrt{Hz}}$ (对于加速度计)。$\frac{1}{\sqrt{Hz}}$ 来源于功率谱密度 (Power Spectral Density, PSD) 的定义和单位。白噪声的 PSD 在整个频率范围内是常数 $S_{nn}(f)={\sigma }_g^2$(单位: $(rad/s{)}^2/Hz$)。标准差 ${\sigma }_g$ 是 PSD 的平方根，因此带上 $\frac{1}{\sqrt{Hz}}$。

这个过程可以在离散时间下模拟如下：

$$n_d[k]={\sigma }_{g_d}w[k]$$

其中

$$w[k]\sim \mathcal{N}(0,1)$$

$${\sigma }_{g_d}={\sigma }_g\frac{1}{\sqrt{\Delta t}}$$

• • 解释: 计算机处理和 Kalibr 算法是在离散时间点 $k$ (对应时间 $t_k=k\Delta t$) 上工作的。需要将连续时间白噪声模型转化为离散形式。

  • $w[k]$: 一个离散时间高斯白噪声序列。每个采样点 $k$的值独立地从标准正态分布 $\mathcal{N}(0,1)$ (均值为 0, 方差为 1) 中抽取。

  • ${\sigma }_{g_d}$: 离散时间白噪声 $n_d[k]$ 的标准差。

  • ${\sigma }_{g_d}={\sigma }_g\frac{1}{\sqrt{\Delta t}}$: 这是关键的离散化公式。它建立了连续时间噪声密度 ${\sigma }_g$和离散时间噪声标准差 ${\sigma }_{g_d}$ 之间的关系。

  • 物理意义: 采样间隔 $\Delta t$ 越小（采样率 $1/\Delta t$ 越高），离散化后的噪声 $n_d[k]$ 在每个采样点上的标准差 ${\sigma }_{g_d}$ 就越大。这是因为更高的采样率允许更多的噪声能量通过抗混叠滤波器进入离散信号。但请注意，总的噪声功率（方差）在一个固定时间段内是相同的，只是被分配到更多（或更少）的采样点上了。

零偏

在Kalibr中，传感器零偏的慢速变化用"布朗运动"过程建模，也称为"维纳过程"，或在离散时间中称为"随机游走"。形式上，这个过程是通过积分强度为${\sigma }_{b_g}$（陀螺仪）或${\sigma }_{b_a}$（加速度计）的"白噪声"生成的：

$$\dot{b_g}(t)={\sigma }_{b_g}w(t)$$

• • 解释: 这是零偏 $b_g(t)$ 变化的连续时间模型。
  • $\dot{b_g}(t)$: 陀螺仪零偏随时间 $t$ 的导数（变化率）。
  • $w(t)$: 一个单位强度的连续时间白噪声过程。它的统计特性与 $n(t)$ 类似：$E[w(t)]=0$, $E[w(t_1)w(t_2)]=\delta (t_1-t_2)$。
  • ${\sigma }_{b_g}$: 驱动零偏变化的噪声的强度，称为 “随机游走系数 (Random Walk Coefficient)”。
  • 含义: 零偏的变化率 $\dot{b_g}(t)$ 本身被建模为一个白噪声过程 ${\sigma }_{b_g}w(t)$。这意味着零偏 $b_g(t)$本身是一个维纳过程 (Wiener Process) 或 布朗运动 (Brownian Motion)。它的路径是连续的，但处处不可微。它的变化是随机的，且增量独立。具体来说，在任意两个不同时间区间 $[t_1,t_2]$ 和 $[t_3,t_4]$ (不重叠) 内，零偏的变化量 $b_g(t_2)-b_g(t_1)$ 和 $b_g(t_4)-b_g(t_3)$ 是相互独立的随机变量。
  • gyroscope_random_walk和accelerometer_random_walk参数指定了这些噪声强度${\sigma }_{b_g}$和${\sigma }_{b_a}$。陀螺仪或加速度计的零偏变化越大，这些参数就需要设置得越高。

这个过程可以在离散时间下模拟如下：

$$b_d[k]=b_d[k-1]+{\sigma }_{bgd}w[k]$$

其中

$$w[k]\sim \mathcal{N}(0,1)$$

$${\sigma }_{bgd}={\sigma }_{b_g}\sqrt{\Delta t}$$

• • 解释: 这是零偏随机游走模型在离散时间步$k$ 上的实现。
  • $b_d[k]$: 离散时间点 $k$ 上的零偏值。
  • $b_d[k-1]$: 前一个离散时间点 $k-1$ 上的零偏值。
  • ${\sigma }_{bgd}$: 离散时间随机游走过程的步长标准差。
  • ${\sigma }_{bgd}={\sigma }_{b_g}\sqrt{\Delta t}$: 这是关键的离散化公式。它建立了连续时间随机游走系数 ${\sigma }_{b_g}$ 和离散时间步长标准差 ${\sigma }_{bgd}$ 之间的关系。
  • 物理意义: 零偏在离散时间步之间的变化量 $\Delta b_d[k]=b_d[k]-b_d[k-1]$ 是一个均值为 0、方差为 ${\sigma }_{b_g}^2\Delta t$ 的高斯随机变量。零偏的不确定性（标准差）随时间增长，增长速率与 $\sqrt{t}$ 成正比。例如，经过时间 $T$，零偏变化的标准差约为 ${\sigma }_{b_g}\sqrt{T}$。采样间隔 $\Delta t$ 越大，每一步允许的零偏变化幅度 ${\sigma }_{bgd}$ 也越大。

Kalibr中的噪声模型参数

在Kalibr中，传感器误差是针对每个传感器轴独立建模的。：

$$E[\mathbf{n}(t)]=0_{3\times 1}$$

$$E[\mathbf{n}(t_1){\mathbf{n}}^T(t_2)]={\sigma }_g^2{\mathbf{I}}_{3\times 3}\delta (t_1-t_2)$$

零偏变化（“随机游走”）也是在每个传感器轴上独立建模的。

随机游走参数的作用？

• 影响状态估计精度：${\sigma }_b$ 越大，Kalibr 对 IMU 的信任度越低，更依赖相机矫正。
• 失效案例：
  • ${\sigma }_b$ 低估 → IMU 权重过高 → 标定结果发散。
  • ${\sigma }_b$ 高估 → 忽略有效 IMU 信息 → 标定误差增大。

---

表1: Kalibr的IMU配置YAML文件中可以指定的IMU噪声模型参数摘要。

参数	YAML元素	符号	单位
陀螺仪"白噪声"	gyroscope_noise_density	${\sigma }_g$	$\frac{rad}{s}\frac{1}{\sqrt{Hz}}$
加速度计"白噪声"	accelerometer_noise_density	${\sigma }_a$	$\frac{m}{s^2}\frac{1}{\sqrt{Hz}}$
陀螺仪"随机游走"	gyroscope_random_walk	${\sigma }_{b_g}$	$\frac{rad}{s^2}\frac{1}{\sqrt{Hz}}$
加速度计"随机游走"	accelerometer_random_walk	${\sigma }_{b_a}$	$\frac{m}{s^3}\frac{1}{\sqrt{Hz}}$
IMU采样率	update_rate	$\frac{1}{\Delta t}$	$Hz$

如何获取你的IMU的参数

来自IMU的数据手册

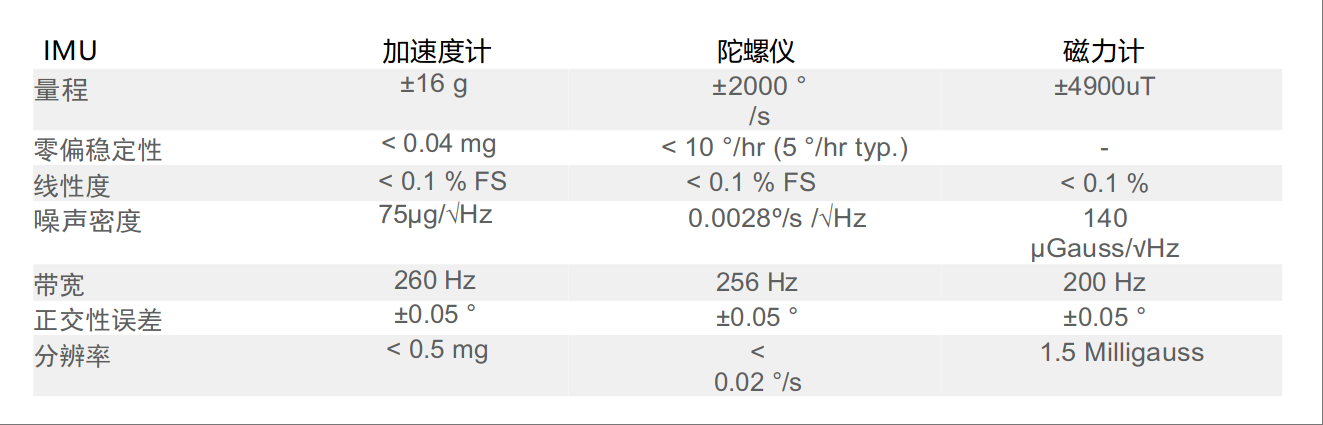
白噪声项: “白噪声"过程的参数（${\sigma }_g$, ${\sigma }_a$）通常在传感器制造商的数据手册中指定。有点误导的是，它们通常被称为角度随机游走（如果是陀螺仪）和速度随机游走（如果是加速度计）。这个名字来源于这样一个事实，即如果在导航方程中积分速率或加速度上的这种白噪声，它会变成角度或速度上的"随机游走”。

其他制造商直接将其指定为速率噪声密度、加速度噪声密度或简称为噪声密度。这个名字来源于这样的事实，即${\sigma }_g^2$对应于$n$的功率谱密度。使用上面概述的离散时间实现，你可以检查是否正确解读了数据手册中的值。

零偏项: 与"白噪声sigma"相反，${\sigma }_{b_g}$和${\sigma }_{b_a}$很少在数据手册中直接指定。原因是，在实践中，对于较长的积分时间，零偏并不真正表现为"随机游走"。通常，所谓的零偏稳定性反而会被指定。这个传感器参数指示了（大约）确定零偏的准确性（如果一个随机过程是"白噪声"和一个"随机游走"零偏的总和，那么在任何时间点都不能以任意低的不确定性估计零偏）。然而，结合"白噪声"的强度，人们通常可以使用运行内零偏稳定性（Allan标准差的最低点，见下文）来确定${\sigma }_{b_g}$和${\sigma }_{b_a}$的合理值（假设噪声由"白噪声"和一个"随机游走"主导）。

（注：可以直接让客服提供相应数据）

来自Allan标准差（AD）

虽然已经提出了许多（参数和非参数）方法来从样本中（自动）确定噪声模型参数，但从Allan标准差图中导出参数可能是最常见和标准化的过程。推导了不同随机过程的AD，包括Kalibr中使用的"白噪声"（在log-log AD图中斜率为-1/2）和"随机游走"（斜率为+1/2）。噪声模型参数可以直接从Allan标准差确定。

${\sigma }_g$和${\sigma }_a$对应于$AD(\tau =1s)$处的值（见下图中的点(1)）。只有当大多数惯性传感器的噪声功率在大约1Hz频率下主要由"白噪声"主导时才是正确的。

${\sigma }_{b_g}$和${\sigma }_{b_a}$被识别为在积分时间为$\tau =3s$时（拟合的）"随机游走"直线对应的值（见下图中的点(2)）。

---

图1: MEMS陀螺仪的Allan标准差，手动识别的噪声过程。

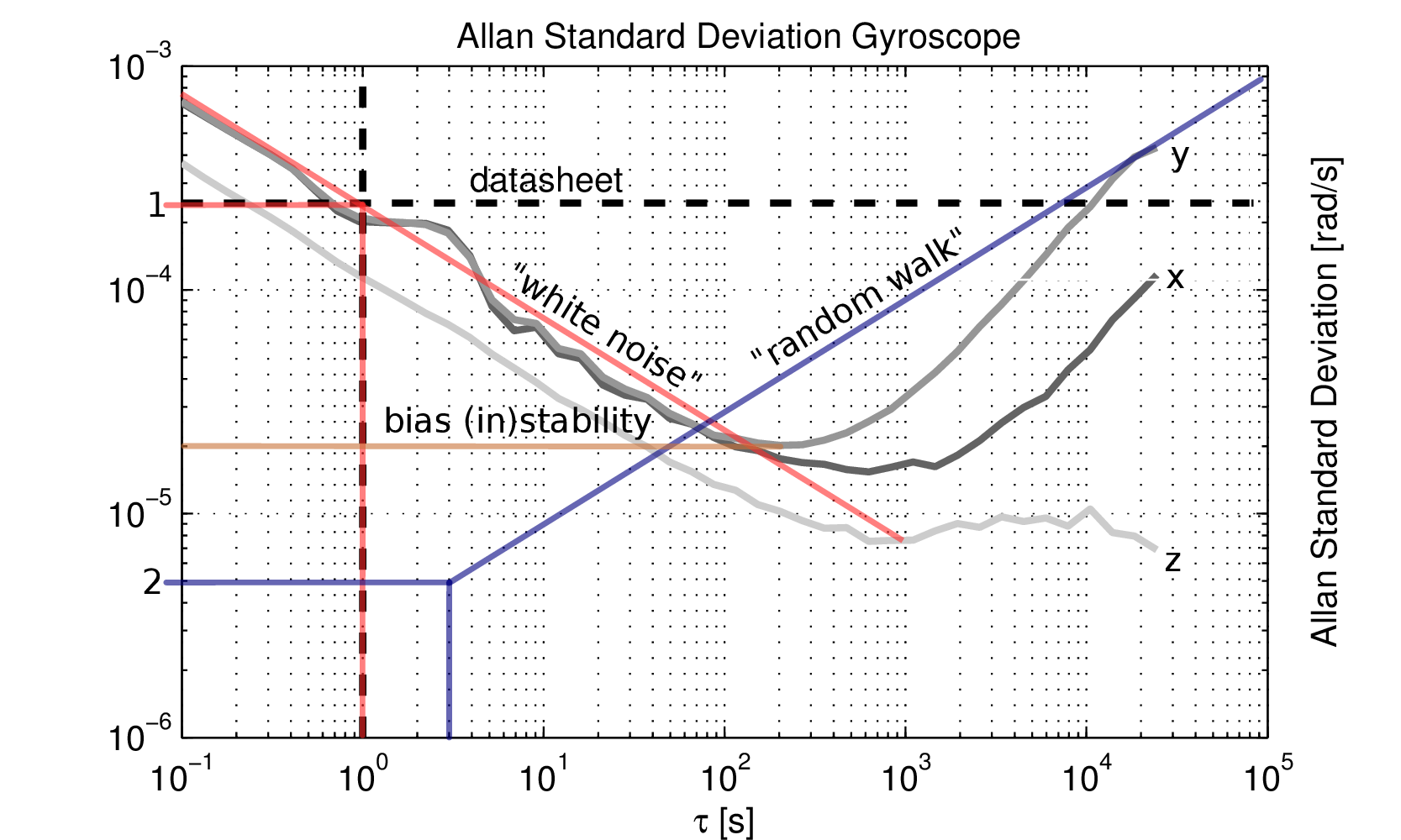
艾伦方差分析是揭示 IMU 各种噪声源在不同时间尺度上贡献的标准方法。Kalibr 使用的 IMU 噪声模型（白噪声 + 随机游走零偏）在 AD 图上表现出特征性的“V”形或“U”形曲线：

1. 短时间尺度 (小 $\tau$)：白噪声 (White Noise) 主导。AD 值随 $\tau$ 增加而减小，表现为 -1/2 斜率。
2. 中等时间尺度 (特定 $\tau$)：白噪声的影响衰减，随机游走零偏的影响开始显现但尚未完全主导。此时 AD 值达到最低点，这个最低点对应的值就是 零偏稳定性 (Bias Instability)。
3. 长时间尺度 (大 $\tau$)：随机游走零偏主导。AD 值随 $\tau$ 增加而增大，表现为 +1/2 斜率。这条 +1/2 斜率线的延伸，就定义了随机游走系数 ${\sigma }_b$。

Kalibr IMU噪声参数的实际应用

一些制造商在设备的数据手册中提供了Allan标准差图。否则，需要从传感器数据中计算。
一个有用的开源工具是ori-drs/allan_variance_ros，似乎有积极维护。
我们建议直接在约15-24小时的IMU静止数据集上使用此工具。

这里使用的IMU测量误差模型是基于未经历运动且温度恒定的传感器推导出来的。因此，例如，由温度变化引起的尺度因子误差和零偏变化未被考虑在内。显然，这个模型过于乐观。特别是当使用低成本MEMS IMU与Kalibr一起工作时，可能需要增加噪声模型参数以"捕捉"这些误差。换句话说，如果你直接使用从静态传感器数据中获得的"sigmas"，Kalibr会倾向于过于信任你的IMU测量，其解决方案不会是最优的。

根据我们的经验，对于最低成本的传感器，可能需要将噪声模型参数增加10倍或更多。如果你使用这样的设备与Kalibr一起工作，请给我们反馈，以便我们可以开发具体的指南、设备特定的参数建议或更高级的方法来确定这些参数。
配置 YAML 文件时，只需提供连续时间参数 (${\sigma }_g,{\sigma }_{b_g}$) 和采样率，Kalibr 内部自动完成离散化计算。

---

连续时间与离散时间标准差关系的推导基于随机过程理论和采样原理，核心在于理解连续白噪声的统计特性如何通过理想采样转化为离散噪声。以下是详细推导过程：

一、加性白噪声的离散化关系

关系式：
离散白噪声标准差$${\sigma }_d=\sigma \frac{1}{\sqrt{\Delta t}}$$
$\sigma$ 是连续时间噪声密度，$\Delta t$是采样间隔。

推导步骤：

1. 连续白噪声的功率谱密度 (PSD)
   连续白噪声 (n(t)) 的功率谱密度为常数：
   $$S_{nn}(f)={\sigma }^2\text{(单位：}{\text{(rad/s)}}^2/\text{Hz)}$$
   这表示其能量在所有频率上均匀分布。

2. 理想采样系统的带宽限制
   当采样率为 $f_s=1/\Delta t$ 时，理想抗混叠低通滤波器会限制信号带宽至奈奎斯特频率：
   $$f_{\text{max}}=\frac{f_s}{2}=\frac{1}{2\Delta t}\text{Hz}$$
   系统带宽 $B=f_{\text{max}}-(-f_{\text{max}})=\frac{1}{\Delta t}$ Hz（双边带宽）。

3. 离散噪声的方差计算
   离散噪声的方差 (\sigma_d^2) 等于 PSD 在系统带宽内的积分：
   $${\sigma }_d^2={\int }_{-f_{\text{max}}}^{f_{\text{max}}}{S}_{nn}(f)df={\int }_{-1/(2\Delta t)}^{1/(2\Delta t)}{\sigma }^{2}df$$
   由于$S_{nn}(f)$ 是偶函数：
   $${\sigma }_d^2=2\cdot {\sigma }^2{\int }_0^{1/(2\Delta t)}df=2\cdot {\sigma }^2\cdot \frac{1}{2\Delta t}=\frac{{\sigma }^2}{\Delta t}$$

4. 离散标准差
   $${\sigma }_d=\sqrt{{\sigma }_d^2}=\sqrt{\frac{{\sigma }^2}{\Delta t}}=\sigma \frac{1}{\sqrt{\Delta t}}$$

物理意义

• 更高采样率 → 更大离散噪声标准差：
  当 $\Delta t$ 减小（采样率升高），离散噪声 ${\sigma }_d$ 增大。这是因为更多高频噪声通过系统带宽被采样。
• 总噪声功率守恒：
  在固定时长 (T) 内，总噪声能量不变：
  $$\text{总能量}={\sigma }_d^2\times (\text{采样点数})=\left(\frac{{\sigma }^2}{\Delta t}\right)\times \left(\frac{T}{\Delta t}\right)={\sigma }^{2}T\cdot \frac{1}{\Delta t}$$
  但实际应用中，离散噪声的方差需按采样率缩放以保持统计一致性。

---

二、随机游走（零偏）的离散化关系

关系式：
离散随机游走步长标准差 ${\sigma }_{bd}={\sigma }_b\sqrt{\Delta t}$ （${\sigma }_b$是连续时间随机游走系数）

推导步骤：

1. 连续时间模型
   零偏变化率是白噪声：
   $$\dot{b}(t)={\sigma }_{b}w(t),E[w(t_1)w(t_2)]=\delta (t_1-t_2)$$

2. 离散时间零偏变化
   在时间间隔 (\Delta t) 内积分：
   $$b(t_k)-b(t_{k-1})={\int }_{t_{k-1}}^{t_k}{\sigma }_{b}w(\tau )d\tau$$

3. 计算方差
   定义积分变量 $I={\int }_{t_{k-1}}^{t_k}w(\tau )d\tau$，其方差为：
   $$\text{Var}(I)=E\left[{\left({\int }_{t_{k-1}}^{t_k}w(\tau )d\tau \right)}^2\right]$$
   展开平方项：
   $$E\left[{\int }_{t_{k-1}}^{t_k}{\int }_{t_{k-1}}^{t_k}w(\tau )w(s)d\tau ds\right]={\int }_{t_{k-1}}^{t_k}{\int }_{t_{k-1}}^{t_k}E[w(\tau )w(s)]d\tau ds$$
   代入白噪声的自相关函数 $E[w(\tau )w(s)]=\delta (\tau -s)$：
   $$\text{Var}(I)={\int }_{t_{k-1}}^{t_k}{\int }_{t_{k-1}}^{t_k}\delta (\tau -s)d\tau ds$$
   对 $\tau$ 积分时，$\delta (\tau -s)$ 仅在 $\tau =s$ 处非零，因此：
   $$\text{Var}(I)={\int }_{t_{k-1}}^{t_k}\underset{=1}{\underbrace{\left({\int }_{t_{k-1}}^{t_k}\delta (\tau -s)d\tau \right)}}ds={\int }_{t_{k-1}}^{t_k}1ds=\Delta t$$

4. 离散步长标准差
   零偏变化的方差为：
   $$\text{Var}\left(b(t_k)-b(t_{k-1})\right)={\sigma }_b^2\cdot \text{Var}(I)={\sigma }_b^2\Delta t$$
   因此标准差为：
   $${\sigma }_{bd}={\sigma }_b\sqrt{\Delta t}$$

物理意义

• 更长采样间隔 → 更大零偏变化：
  $\Delta t$ 越大，零偏在一步内的随机变化幅度 ${\sigma }_{bd}$ 越大，符合随机游走的累积效应。
• 零偏不确定性随时间增长：
  经过时间 $T=N\Delta t$，零偏变化的标准差为 ${\sigma }_b\sqrt{T}$，体现随机游走的扩散特性。

---

关键对比总结

噪声类型	连续 → 离散关系	依赖采样间隔	物理原因
加性白噪声	${\sigma }_d=\sigma /\sqrt{\Delta t}$	$\propto 1/\sqrt{\Delta t}$	系统带宽增加，捕获更多噪声能量
随机游走	${\sigma }_{bd}={\sigma }_b\sqrt{\Delta t}$	$\propto \sqrt{\Delta t}$	时间间隔增长，零偏累积效应增强

---