考研408《计算机组成原理》复习笔记,第二章(2)数值数据的表示和运算(浮点数篇)
一、回顾定点数知识点
——定点小数机器码表示
——定点整数机器码表示
——【原码】和【移码】的作用
二、浮点数表示
1、概念引入
我们生活中有很多 “带小数”,也就是浮点数,也就是【整数部分】和【纯小数部分】都不为0,那么这样的小数是不可以按之前【定点数】的形式表达的,如下图:
定点数的小数点是固定死的,这样就不够灵活,无法应对对整数或小数要求高精度的表达方式
我们有时会有对整数或小数单独要求高精度的需求
所以我们希望小数点是可以浮动的,并不是固定在最左或最右,而小数点的位置和正负号这些规则都能按照一个规则来计算出来
那么我们希望用专门的浮点数表示规则来表示【浮点数】
于是参考十进制表示浮点数的形式,小数点可以浮动,【一个带小数 * 10的不同幂次】可以表示一个浮点数(即数学里的 “科学计数法”!!)
我们会发现:当小数点往左移动一位(整数变小),为了保证原数值不变,就要乘一个2;小数点往右移(整数变小),为了保证数值不变,就要除一个2;
简而言之:2的次幂对于小数点的移动是【左加右减】(不用自己算,知道就行,例子如下)
2、二进制浮点数的“科学计算法”公式
那么我们得出了【二进制表示浮点数】的公式:
我留意到网上大部分公式都是这样,这其实是简化的公式,没有考虑正负号的(了解有这么回事就行,不然会像我一开始发现负数对不上这个公式而懵逼。。。)
(忽略正负符号的形式)
;
实际上,准确的公式应该是
(不忽略正负符号的准确形式)
解释:
- N:浮点数真值
- S:是整个浮点数的符号,正数S=0、负数S=1
- M:尾数,即0.11 * 2^2、1.1 * 2^1、11 * 2^0......红色部分(非正式数,仅作例子)
- 通常是一个定点整数,用原码表示
- 但是不管是普通浮点数还是后面学的IEEE754浮点数,整数部分都会被规定死是一个约定好的数(普通浮点数,整数那就是0;IEEE754浮点数,整数那就是1),所以也没必要存它,大家都心知肚明这是什么数(具体规则后面会解释)
- 结论:所以【M(尾数)】实际只由【小数部分】代表
- R^E:阶数,即0.11 * 2^2、1.1 * 2^1、11 * 2^0......黄色部分(非正式数,仅作例子)
- 其中R是基数,二进制通常都是2,所以大家都知道R=2就没必要存它了(有时也会约定为2、4、16,但正常情况都是2)
- E是阶码或指数,这是不定的,所以要存储(通常是一个定点小数,用移码表示)
- 结论:所以【阶数】实际上也只由【E阶码(或指数)】代表
(暂时忽略符号)
;
总结:
- 1、N= (-1)^S × M × R^E ————> 真值 = (-1)正负号 × 尾数 × 阶数
- 2、实际尾数只用【尾数的小数部分】表示
- 3、实际阶数只用【阶数的指数部分】表示
3、浮点数机器码规则
1)浮点数机器码的组成
那么实际的机器码是如何表示刚刚的公式的?
- 1、三部分:【整个浮点数的符号位】+【阶码】+【尾码】
- 2、其中【阶码】包含了【阶符 (阶数的正负号)】和【阶数 (切记只是指数部分)】
- 3、其中【尾码】就是【尾数 (切记,只是是小数部分)】
(这里可能会有人不理解,为什么在尾数后面补0?之前【零扩展】和【符号扩展】不都是在前面补0吗?因为tmd这尾数是【小数部分】啊,小数部分后面补0和原来的值有什么区别???)
2)求阶码的公式
但是这里需要重点注意【阶码】部分,【阶码】不只单纯是原来阶数的值
我们前面学过【移码】,【浮点数的阶码】就是用【移码】表示
(因为其他码会让机器在比较大小时误认为负数大于正数,而移码可以明确比较正数值大于负数值,不理解的看我之前的文章: 考研408《计算机组成原理》复习笔记,第三章数值数据的表示和运算(定点数篇)-CSDN博客, 也不是重要知识点)
;
;
那么牢记这两个公式:
并且注意,全部按照 “无符号数形式” 去计算
;
例子1:
阶码是7位,则阶码的真值7-1=6位,应该是【偏置值 = 2^6 =64】
3)浮点数和真值之间转换
根据这个公式就可以推导浮点数转换
【浮点数真值——>浮点数机器码】
假设条件:
32位的浮点数,其中阶码7位,尾数24位
真值是:-0.011001000000000000000000
【浮点数机器码——>浮点数真值】
假设条件:
32位的浮点数,其中阶码7位,尾数24位
机器码是:1 10101111 011001000000000000000000
4)浮点数机器码可表示范围
如何理解上面的范围,看下面例子解释:
以 “32位的浮点数,其中阶码7位,尾数24位” 为例子
;
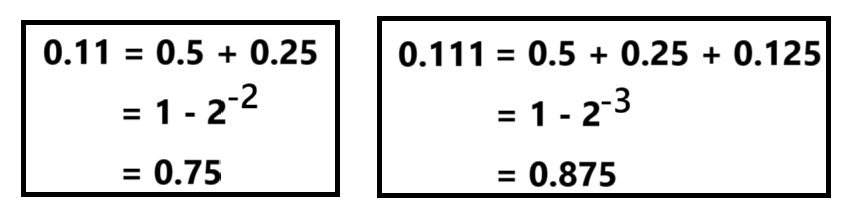
首先前提知识点:我们知道N位的定点整数数部分连续全是1的话,其值就是【2^N-1】;而N位的定点小数如果后面连续全是1的话,其值就是【1-2^-N】,比如0.111就是1-2^-3=0.875
;
1、先看【正数】情况
- 最大值
(当然【阶码真值】你也可以按【移码最大值2^(N-1)-1】求得)
- 最小值
(当然【阶码真值】你也可以按【移码最小值-2^(N-1)】求得)
- 溢出
正数部分超出最大值叫正上溢、超出最小值的范围是正下溢,正下溢部分一般直接当作0处理;正上溢部分后面讲规格化的时候才会涉及,暂时不说
;
2、再看负数,知道正数范围就可以推负数范围了
- 最大值
- 最小值
- 溢出
负数部分超出最小值叫负上溢、超出最大值的范围是负下溢,负下溢部分一般直接当作0处理(正下溢和负下溢都称 “下溢”);正上溢部分后面讲规格化的时候才会涉及,暂时不说(正上溢和负上溢都叫 “上溢”)
4、普通浮点数规格化
1)为什么规格化
那么我们前面我们在研究浮点数真值和机器码转换的时候反复提到,知道【尾码】就默认知道【尾数】是【0.尾码】,整数部分固定是0,究竟有什么道理?
首先十进制的最正确的科学计数法应该是【整数部分只有1位】,二进制也是
然后尾数的位数决定了浮点数的有效数位,假设只能保留有限的几位小数的话,那么肯定是非零的小数部分保留的越多,精度越高。所以为了让有效数位占满尾数数位,我们必须进行规格化。
2)怎么规格化
规格化就是通过调整【阶码】和【尾码】,使得一个非零的浮点数在【尾数的最高位上】是一个有效数值!
具体措施:【左规】和【右规】
左规就是整数和小数点不动,小数部分往左移(其实就是小数点往后移位)
右规就是整数和小数点不动,小数部分往右移(其实就是小数点往前移位)
规格化后的机器码尾码是啥样的?
补充:不同基数r,会导致不同的规格化
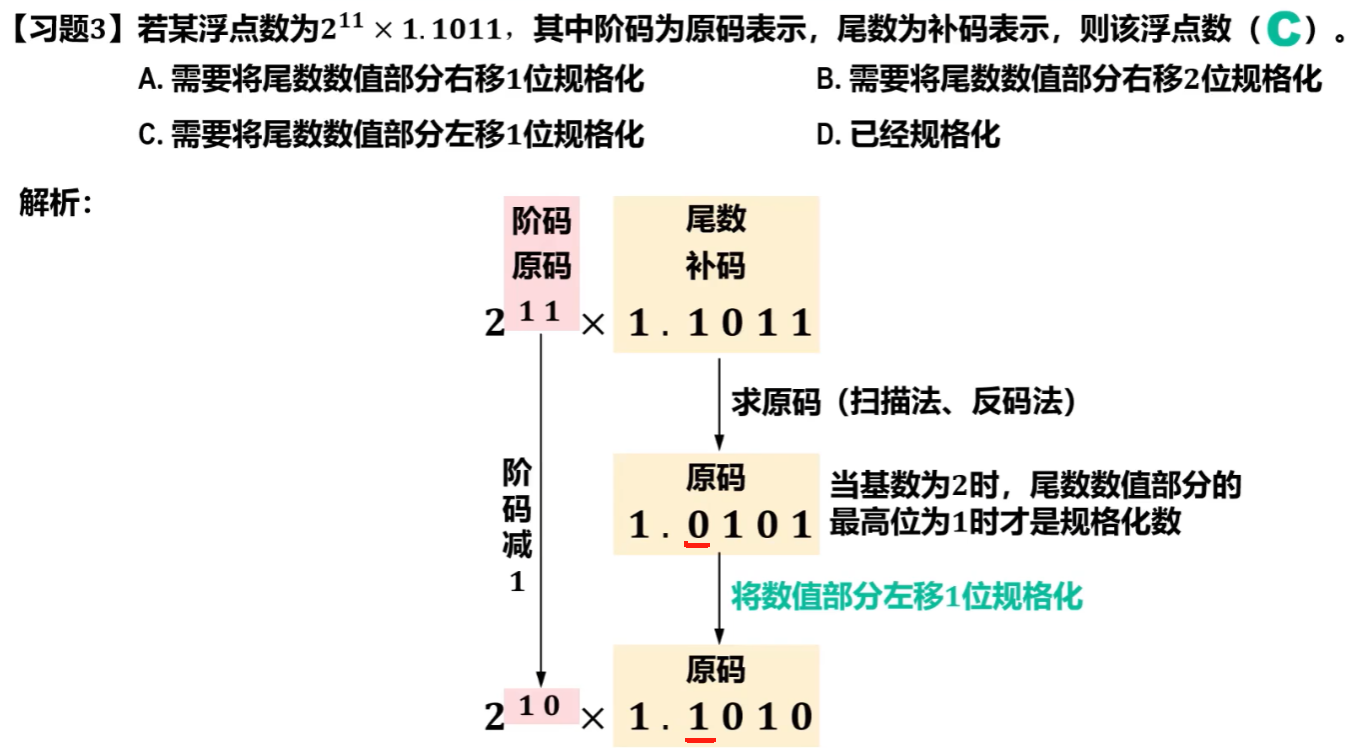
3)例题
5、IEEE 754规范
1)表示规则
但是那帮研究计算机的逼养的还是不爽啊,就非还要在整一些新的规则出来,好嘛没办法,最后IEEE754这套浮点数规范就是一直沿用至今的一套规范。

他要求就两种浮点数表示法:
- 1、单精度浮点数Float
- 4字节 (32位),其中1符号位、8阶码位、23位尾码(记牢了!!!!)
- 【偏置值】:2^(8-1)-1 = 127位( 区分一下,普通浮点数是2^(N-1) )
- 2、双精度浮点数Double
- 8字节 (64位),其中1符号位、11阶码位、52位尾码(记牢了!!!!)
- 【偏置值】:2^(11-1)-1 = 1023位( 区分一下,普通浮点数是2^(N-1) )


留意和【普通浮点数】的区别:
- 1、同样位数的阶码条件下,【IEEE754】的【偏置值】比【普通浮点数】的【偏置值】偏置值多1,而且IEEE754的移码的【全1】和【全0】有别的用途,阶码不能用这两(下图是32位的单精度的阶码例子)
- 2、普通浮点数在规格化后也只是尾数最高位是1,而IEEE754浮点数要求是整数部分是1!!!
(没什么办法去理解,很无奈我本人也看遍了全网所有视,没有一个解释清楚的,只能死记硬背。。。。。。)
2)IEEE754浮点数机器码和真值的转换
【浮点数机器码——>浮点数真值】
【浮点数真值——>浮点数机器码】
3)IEEE754浮点数机器码可表示范围
解释:
只以单精度为例子,注意这里【阶码】我就不按普通浮点数那么细致地用偏置值算了,直接用【移码】可表示地最大最小值来推导即可
;
【规格化情况】:整数部分是1,值 = 1 + 小数部分
【正数情况】
1、最小值(阶码是: - (移码最小值绝对值-2) )
;
2、最大值(阶码是: 移码最大值 )、
;
【负数情况】
没什么好说的,【负数最小值】就是【 - 正数最大值】,【负数最大值】就是【- 正数最小值】,加个负号的事
;
;
;
;
【非规格化情况】:
- 1、整数部分为0,值 = 0 + 小数部分
- 2、阶码全0,尾码不全为0
- 3、偏置值是126(别问为啥那么,我tm也不知道,全网没人讲为什么,只能死记硬背)
【正数情况】
1、最大值
2、最小值
【负数情况】
没什么好说的,【负数最小值】就是【 - 正数最大值】,【负数最大值】就是【- 正数最小值】,加个负号的事
;
4)解惑:为什么IEEE754的阶码是移码,但不能和补码转换再求真值?
因为我们要记住:
- 1、普通浮点数的偏置值是正常的,偏置值是【2^(N-1)】时,阶码可以按照【移码<——>补码】原则(移码和补码就是符号位取反,其他位一样)
- 2、IEEE754浮点数的偏置值是不正常的!!他的偏置值是【2^N-1】,所以不可以用【移码<——>补码】
5)IEEE754规格化
没什么好说的,就区别于普通浮点数:要把整数部分规格化成一个1,最终变成【1.M】形式就行
6)需要死记硬背的知识点
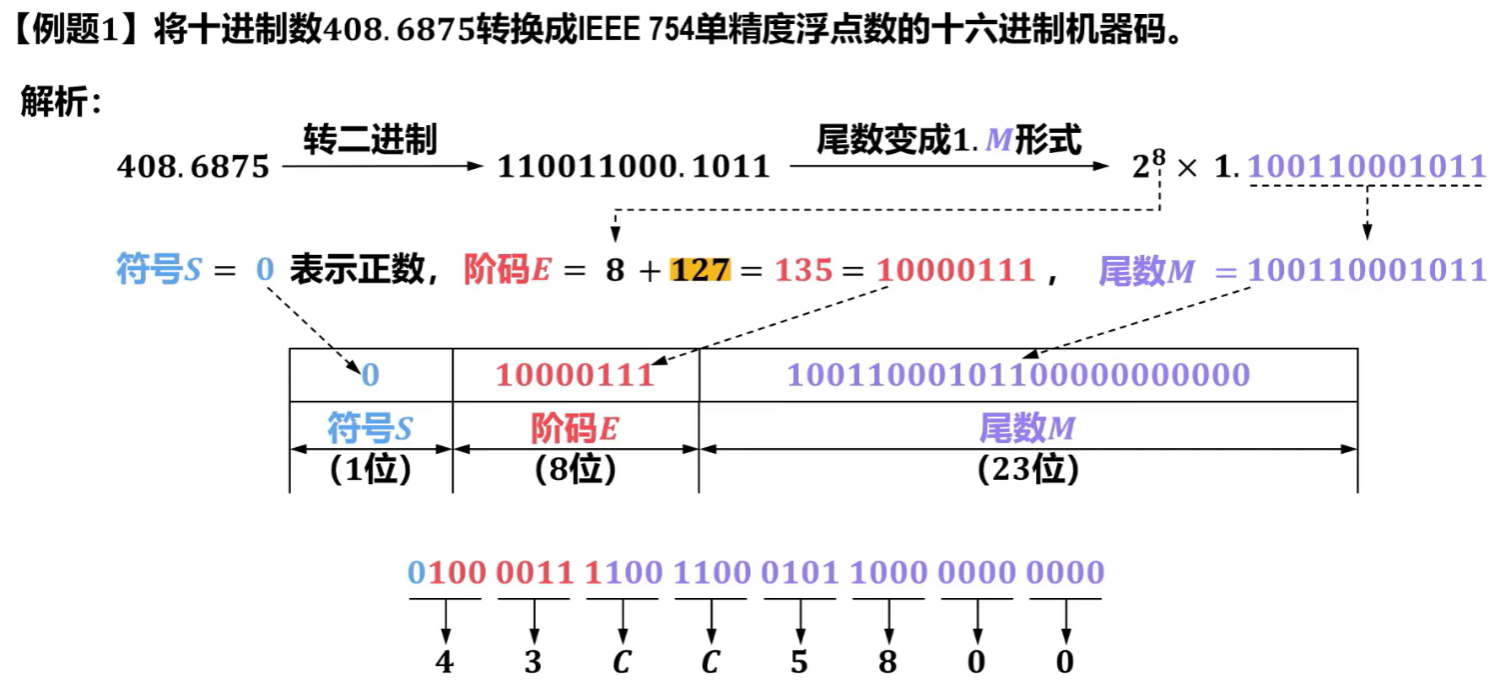
7)转换类型例题
小技巧:可以留意float的浮点数机器码后面0~20(后5个字节)基本都是为了补0的没用数,然后这些数可以直接不看了,浪费时间