当前位置：首页 > ds >正文

最大熵逆强化学习

ds 2025/5/15 6:13:25

## 解决问题

## 具体算法

## 推导过程

### 高效统计每个状态下的频次

## 优点

1.提升确定性与探索性

2.能够解决Label Bias问题：Conditional Random Field literature

1. 动作基分布的核心特点

2. 标签偏差（Label Bias）问题

3. 对IRL的负面影响

4. 最大熵路径分布的优势

## 局限性

## 总结

参考：

## 解决问题

逆强化学习：目标是从专家的行为数据中推断出隐含的奖励函数。一旦得到了奖励函数，就可以用强化学习的方法来训练新的智能体执行任务。

最大熵：在满足已知约束的条件下，概率分布应该尽可能均匀，即保留最大的不确定性。这样可以避免模型做出过于武断的假设，尤其是在数据有限或者存在噪声的情况下，模型更鲁棒。

解决次优演示下的路径分布歧义：

核心矛盾：当专家演示行为不是完全最优时，可能存在无数种不同的路径分布都能匹配专家特征期望（即满足约束 E[f]= $\tilde{f}$ ）。
歧义性：这些分布可能对路径存在“额外偏好”（例如偏好某些无关特征或路径），但这些偏好并未体现在数据中。
示例：假设两种路径A和B的特征期望相同，但某个分布赋予A更高概率，而另一个分布赋予B更高概率。这种偏好缺乏数据支持，需消除。

MaxEnt IRL：

应用到逆强化学习中，它假设专家轨迹的分布服从一个指数族分布，其概率与轨迹的累计奖励呈指数关系。也就是说，轨迹的累计奖励越高，其出现的概率越大。同时，整个分布的熵要尽可能大。这样，模型在拟合专家数据的同时，不会对未观察到的数据做过多假设。

核心思想：在所有满足特征期望的分布中，选择熵最大（即最不确定、最无偏）的分布。
数学意义：最大熵分布是唯一满足约束且不引入额外假设的分布（符合奥卡姆剃刀原则）。
直观解释：
- 若两条路径的特征贡献相同，则它们的概率相等。
- 仅通过特征期望的差异来区分路径概率，避免主观偏好。

## 具体算法

定义特征向量：状态或状态-动作对映射到特征空间。奖励函数通常表示为这些特征的线性组合，即权重向量与特征向量的点积： $r(s) = \theta ^T f(s)$
定义概率模型：
路径ζ的概率由指数奖励加权，参数化为奖励权重θ
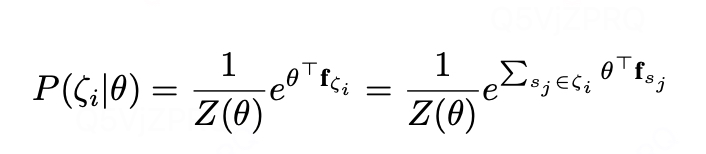
最大熵学习：

目标：从专家演示数据中学习策略，使策略的熵最大，同时匹配专家的特征期望。
优化问题：
- 最大化对数似然：
- 约束条件：学习策略的特征期望 E[f]必须等于专家特征期望 $\tilde{f}$ 。

4. 梯度更新：

梯度是专家特征期望与学习策略特征期望的差。

计算状态访问频率 $D_{s_i}$ （即每个状态被访问的概率）。
用 $D_{s_i}$ 加权特征 $f_{s_i}$ ，得到学习策略的特征期望。

当梯度为零时，学习策略的特征期望与专家完全匹配。

得到参数，进而得到奖励函数，再通过强化学习训练策略

## 推导过程

最大熵模型的学习等价于以下约束最优化问题：

其中 $P(\tau)$ 为某条轨迹 $\tau={s_1, s_2, ..., s_T}$ 的概率； $f_{\tau}=\sum_tf(s_t)$ 为特征， $\tilde{f}$ 为特征期望；

求解方式为将约束最优化的原始问题转换为无约束最优化的对偶问题（具体推导过程可以参考统计学习方法）

先求解 $P_{\lambda}(\tau)$ :

(最大熵模型)

再求解参数 $\lambda$ (最大熵模型中的参数向量)；

对偶函数的极大化等价于最大熵模型的极大似然估计。

使用专家示例轨迹集，进行上述最大似然估计即可求得 λ ，从而得到奖励函数：

$r(s) = \lambda ^T f(s)$