【三】 空域滤波的基础与空域中的低通滤波器（2）【830数字图像处理】

4 空间滤波的基础

“滤波”是指通过、修改或抑制图像的规定频率分量。

• 通过低频分量【背景】的滤波器称为低通滤波器，用于去噪，平滑图像。
• 通过高频分量【细节】的滤波器称为高通滤波器，用于提取边缘信息。

若对图像像素执行的运算是线性的，则称该滤波器为线性空间滤波器，否则为非线性空间滤波器。

4.1 线性空间滤波的原理

线性空间滤波器计算过程：

1. 建立一个与原图像同样大小的$0$矩阵阵列
2. 设置一个滤波器核（一般是3×3大小），核的阵列中是系数值
3. 用核原点对应原图像中的第一个像素，然后计算整个滤波器核围住的区域，计算方法就是对应系数和像素值相乘相加
4. 将计算后得到的值放到步骤1中矩阵对应位置
5. 滑动重复上述过程，直到遍历原图中所有像素的值

为了在进行滤波器运算时能够处理图像边缘的像素，通常会对原图像进行边缘填充（也称为边界扩展或零填充）。具体来说，对于大小为 $m\times n$ 的核，填充方式如下：

1. 顶部和底部：在图像的顶部和底部各补$\frac{m-1}{2}$ 行零（ $m$ 是奇数，若为偶数则分别补 $\frac{m}{2}$行），并且确保总的补充行数是 $m-1$。

2. 左侧和右侧：在图像的左侧和右侧各补 $\frac{n-1}{2}$ 列零（ $n$ 是奇数，若为偶数则分别补 $\frac{n}{2}$ 列），确保总的补充列数是 $n-1$。

图3.28说明了用3×3大小的滤波核进行线性空间滤波器的原理。$3\times 3$滤波器核的系数坐标为$$\left(\begin{array}{ccc}w(-1,-1)& w(-1,0)& w(-1,1)\\ w(0,-1)& w(0,0)& w(0,1)\\ w(1,-1)& w(1,0)& w(1,1)\end{array}\right)$$

大小为 $m\times n$ 的核对大小为$M\times N$的图像的线性空间滤波的表达式$$g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)$$

滤波后的像素值通常赋值给新建图像中的对应位置，以保存滤波后的结果。很少出现用滤波后的像素替换原图像中对应位置的值的情况，因为这样做会在执行滤波运算时改变原图像的内容。

4.2 相关运算与卷积运算

相关运算其实就是4.1节中的理论过程，而与空间卷积的唯一区别只是将相关运算的核旋转了180°。当核的值关于其中心对称时，相关和卷积得到的结果相同。

• 相关运算【滤波过程】：在图像上移动核的中心，并且在每个位置计算乘积之和。
• 卷积运算【旋转后执行滤波过程】：将核旋转180°后，在图像上移动核的中心，并且在每个位置计算乘积之和。

一个元素是1，其余元素是0的函数称为离散单位冲激函数。图3.29和图3.30展示了使用离散冲激函数的一维和二维的例子。

为了使用模板对图像进行卷积，需要在图像周围补零，以保证卷积后图像大小不变。大小为 $m\times n$ 的核 $w$ 对与图像 $f(x,y)$ 的相关运算定义为$$(w☆f)(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)$$卷积运算定义为$$(w★f)(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x-s,y-t)$$

得到完全相关或完全卷积阵列的大小为$S_v\times S_h$，其中$$S_v=m+M-1$$ $$S_h=n+N-1$$

有时图像是被顺序地滤波（卷积）的，每个阶段会使用不同的核，即$$w=w_1★w_2★\dots ★w_Q$$若这些核的大小都是$m\times n$，则对于$Q$个阶段的滤波，$w$的大小为$W_v\times W_h$，其中$$W_v=Q\times (m-1)+m$$ $$W_h=Q\times (n-1)+n$$

需要注意的是，在边缘检测、模糊、锐化等图像处理任务中，相关操作通常是直接应用于图像的，因为它简单直观。但是，很多文献和工具会使用“卷积”这个术语，即使实际上没有翻转滤波器。所以，只有在题目明确要求做卷积运算的时候，才将核旋转180°来计算，除此之外，都是直接对图像执行相关运算。

2006、2008、2010甄题【计算题】

（10分）计算二维卷积$\left(\begin{array}{cc}1& 2\\ 3& 3\\ 2& 1\end{array}\right)★\left(\begin{array}{cc}1& 2\\ -2& 1\end{array}\right)=?$

设图像为$f=\left(\begin{array}{cc}1& 2\\ 3& 3\\ 2& 1\end{array}\right)$，核为$w=\left(\begin{array}{cc}1& 2\\ -2& 1\end{array}\right)$，核翻转180°得$w^{\prime }=\left(\begin{array}{cc}1& -2\\ 2& 1\end{array}\right)$
由于核大小为$2\times 2$，因此所需最小填充是在$f$四周添加1个像素为0边框，得到$f_p=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 2& 0\\ 0& 3& 3& 0\\ 0& 2& 1& 0\\ 0& 0& 0& 0\end{array}\right)$
于是，$\left(\begin{array}{cc}1& 2\\ 3& 3\\ 2& 1\end{array}\right)★\left(\begin{array}{cc}1& 2\\ -2& 1\end{array}\right)=f_p★w=\left(\begin{array}{ccc}1& 4& 4\\ 1& 6& 8\\ -4& 2& 5\\ -4& 0& 1\end{array}\right)$

2013甄题【计算题】

【抄一遍公式后只写第二行对应相乘相加的表达也没问题】

2019甄题【计算题】

求出一个矩阵和另外一个矩阵卷积的结果。$f(x,y)=\left(\begin{array}{ccc}1& 9& 3\\ 0& 9& 0\\ 2& 9& 1\end{array}\right)，h(x,y)=\left(\begin{array}{ccc}-1& 2& -1\\ -1& 2& -1\\ -1& 2& -1\end{array}\right)$

由于核大小为$3\times 3$，因此所需最小填充是在$f$四周添加$\lfloor \frac{3}{2}\rfloor =1$个像素为0边框，得到$f_p=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 1& 9& 3& 0\\ 0& 0& 9& 0& 0\\ 0& 2& 9& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right)$

由卷积公式$$(h★f_p)(x,y)=\sum _{s=-1}^1\sum _{t=-1}^{1}w(s,t)f_p(x-s,y-t)$$可得$$\begin{array}{rl}(h★f_p)(1,1)& =w(0,0)f_p(1,1)+w(0,-1)f_p(1,2)+w(-1,-1)f_p(2,2)\\ & =2\times 1+(-1)\times 9+(-1)\times 9=16\end{array}$$ $$\begin{array}{rl}(h★f_p)(1,2)& =w(0,1)f_p(1,1)+w(0,0)f_p(1,2)+w(0,-1)f_p(1,3)+w(-1,0)f_p(2,2)\\ & =(-1)\times 1+2\times 9+(-1)\times 3+2\times 9=32\end{array}$$其他同理，得最后卷积结果为$$\left(\begin{array}{ccc}-16& 32& -12\\ -21& 47& -19\\ -14& 33& -16\end{array}\right)$$

课后习题3.18【计算题】*

(b) 由于核大小仅为 3×3，因此所需的最小填充是在图像四周添加一个像素为 0 的边框。这样，原始图像中的（2,3）点就变成了填充图像中的（3,4）点。我们用符号 $f_p$ 表示 $7\times 7$ 填充图像：


其中第二个等式对应于核以填充图像的$(3,4)$点为中心。唯一不为 0 的乘积总和值是$w(0,0)f_p(3,4)=(4)(1)=4$ 和 $w(-1,0)f(4,4)=(2)(1)=2$。因此，当核以 (2,3) 为中心时，卷积值为 $(w★f)(3,4)=4+2=6$。卷积结果为：

课后习题3.19

相关性和卷积的大小是相同的，因此我们只对相关性证明公式(3-36)和(3-37)的有效性。让 $w$ 表示大小为 $m\times n$ 的核，让 和 $f$ 表示大小为 $M\times N$ 的图像。假设 $m\le M，n\le N$。我们首先证明 $S_h$ 的有效性。假设 $w$ 的右下角点与图像的原点重合，而原点位于图像的左上角。要完成 $w$ 与 $f$ 第一行的关联，使 $w$ 的最左下角点与 $f$ 第一行的最右边点重合，我们必须将 $w$ 向右移动 $n-1$ 次。图像的宽度为 $N$，因此第一行相关结果的总宽度为 $N+n-1$，当然所有行的宽度是相同的。因此，如公式（3-37）所示，相关结果的图像宽度为 $S_h=N+n-1$。垂直方向的类似分析表明，相关结果的高度为 $S_v=M+m-1$，如式（3-36）所示。请记住，这些结果适用于这样的配置，即我们以 $w$ 的最右下角点与 $f$ 的原点（顶部，左侧）重合为起点，以 $w$ 的左上角点与 $f$ 的右下角像素重合为终点。

课后习题3.17

4.3 可分离滤波器核

若二维函数$G(x,y)$可写成一维函数$G_1(x)$和$G_2(x)$的乘积，即$G(x,y)=G(x)G(y)$，则它是可分离的。

滤波器核的秩为1，则核可分离。可分离核滤波器的优点是可以减少计算量，使得计算速度更快。

• 对于大小为$M\times N$的图像和大小为$m\times n$的核，直接进行卷积运算需要 $MNmn$次乘法和$MN(m\times n-1)$次加法运算 。其中，$m\times n-1$是因为核对图像中每个像素进行卷积时，都会少一次加法运算。

例如一个2×2的核对一幅图像中第一个像素点进行卷积运算，那么以该像素点为中心，被滤波器盖住的图像的一个2×2区域的像素与核进行相乘相加，此时乘法次数是4次，加法次数是3次。假设核内元素都是1，该2×2邻域图像中的像素都是0，进行卷积操作有：
$1\times 0+1\times 0+1\times 0+1\times 0=0$，最后的0是卷积输出值，这一次卷积操作我们数一下可以发现，是$2\times 2=4$次乘法和$2\times 2-1=3$次加法。
若图像大小为$M\times N$，要对$M\times N$个像素进行卷积操作，也就是要使用卷积运算$M\times N$次。用一个$2\times 2$的核对该图进行卷积则共需要$4\times M\times N$次乘法和$3\times M\times N$次加法运算。

• 若核是可分离的，对于一个大小为$m\times n$的核可以分离为一个$m\times 1$和一个$1\times n$的核。分别用这两个核对$M\times N$的图像的图像进行卷积：
  • 用$m\times 1$的核需要$MNm$次乘法和$MN(m-1)$次加法运算；
  • 用$1\times n$的核需要$MNn$次乘法和$MN(n-1)$次加法运算。
  • 总共需要 $MN(m+n)$次乘法和$MN(m+n-2)$次加法运算。

综上，使用可分离核相对于不可分离核的计算优势为$$C=\frac{MNmn}{MN(m+n)}=\frac{mn}{m+n}$$

2024甄题【简答题】

（5分）用大小为60×60的可分离滤波器核和不可分离滤波器核去处理一幅图像，请定性分析它们的计算效率。

假定一幅图像的大小为 $M\times N$。

对于大小为 $60\times 60$ 的不可分离滤波器核

• 乘法次数： $MN\times 60\times 60=3600MN$
• 加法次数： $MN\times (60\times 60-1)=3599MN$

对于大小为 $60\times 60$ 的可分离滤波器核

• 乘法次数： $MN(60+60)=120MN$
• 加法次数： $MN(60+60-2)=118MN$

故，可分离核相对于不可分离核的计算优势为$$C=\frac{3600MN}{120MN}=30$$也就是用可分离核比用不可分离核快了30倍

2022甄题【计算题】

二维滤波器$w=\left(\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right)$
（1）将$w$分离为两个一维滤波器；
（2）对于$M\times N$图像进行空间滤波，分别计算使用二维和一维滤波器的计算量（加法和乘法的次数），并说明一维滤波器的优势。

（1）$w=\left(\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right)=\left(\begin{array}{c}1\\ 2\\ 1\end{array}\right)\left(\begin{array}{ccc}1& 2& 1\end{array}\right)=w_1★w_2$
故分离的两个一维滤波器分别为：$w_1={\left(\begin{array}{ccc}1& 2& 1\end{array}\right)}^T，w_2=\left(\begin{array}{ccc}1& 2& 1\end{array}\right)$

（2）对于二维滤波器$w$

• 乘法次数为：$M\times N\times 3\times 3=9MN$
• 加法次数为：$M\times N\times (3\times 3-1)=8MN$

对于一维滤波器$w_1$和$w_2$

• $w_1$和$w_2$的乘法次数均为：$M\times N\times 3=3MN$。于是，总的乘法次数为$6MN$
• $w_1$和$w_2$的加法次数均为：$M\times N\times (3-1)=2MN$。于是，总的加法次数为$4MN$

综上，一维滤波器相对于二维滤波器的计算优势为$$C=\frac{9MN}{6MN}=1.5$$也就是，使用一维滤波器比二维滤波器要快$1.5$倍。

课后习题3.20【计算题】*

（a）$w=\left(\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right)=\left(\begin{array}{c}1\\ 2\\ 1\end{array}\right)\left(\begin{array}{ccc}1& 2& 1\end{array}\right)=w_1★w_2$，即$w_1={\left(\begin{array}{ccc}1& 2& 1\end{array}\right)}^T，w_2=\left(\begin{array}{ccc}1& 2& 1\end{array}\right)$

注： 在求解本问题的（b）和（c）部分时，假设核中心的起始位置与未填充图像的原点重合，如图 3.30 所示。

课后习题3.22【计算题】*

（a）$v$和$w^T$都是一维核，由$v{w}^T$形成的核是秩为1的矩阵，且秩为 1 的核都是可分离的。所以，核是可分离的。

（b）$w=\left(\begin{array}{ccc}1& 3& 1\\ 2& 6& 2\end{array}\right)=\left(\begin{array}{c}1\\ 2\end{array}\right)\left(\begin{array}{ccc}1& 3& 1\end{array}\right)=w_1★w_2$

（c）$w=\left(\begin{array}{cccc}2& 1& 1& 3\\ 4& 2& 2& 6\\ 2& 1& 1& 3\end{array}\right)=\left(\begin{array}{c}1\\ 2\\ 1\end{array}\right)\left(\begin{array}{cccc}2& 1& 1& 3\end{array}\right)=w_1★w_2$

课后习题3.23【证明题】*

(a) 正如本节的开头所述，若函数$G(x,y)$可写成$G(x,y)=G(x)G(y)$，则它是可分离的。二维高斯函数可以写成$$G(x,y)=e^{-\frac{x^2+y^2}{2{\sigma }^2}}=e^{-\frac{x^2}{2{\sigma }^2}}{e}^{-\frac{y^2}{2{\sigma }^2}}=G_1(x)G_2(y)$$因此，高斯核是可分离的。

课后习题3.24

从图 3.28 中，我们知道两个二维函数的卷积是将其中一个函数旋转 180°，然后滑过另一个函数，使一个函数的每个元素都 "访问 "另一个函数的每个元素。[这就是 “完全卷积”，与公式 (3-36) 和 (3-37) 有关。］ 如果我们将 $r$ 旋转 180°，可以得到$$\text{r}=[r_n{r}_{n-1}\dots r_1]$$可以看到，将 $r$ 滑过 $c$ 的第一行会产生卷积元素：$$r_n{c}_1{r}_2{c}_1\dots r_m{c}_1$$等于上述乘积的第一行。不难看出，当 $r$ 滑过 $c$ 的第二行时，将产生乘积的第二行，以此类推，在卷积过程结束时，我们将产生两个向量的整个乘积。

4.4 空域滤波和频域滤波的关系

在空域中使用傅里叶变换可以进入到频域，再用傅里叶反变换可以回到空域。

• 空域中的卷积等效于频域中的乘积，反之亦然。
• 空域中振幅为$A$的冲激是频域中值为$A$的一个常数，反之亦然。

图3.32a是频率域中的一个理想低通滤波器传递函数，它会消除$u_0$以上的所有频率，同时通过低于该值的所有频率。也就是说，这个滤波器在低频和高频之间的过渡是瞬时的，转换到空间域就会出现“振铃”效应。

4.5 如何构建空间滤波器核

第一种：根据其数学性质。例如计算邻域像素平均值的滤波器会模糊图像。

第二种：对形状具有所需性质的二维空间函数进行取样。例如后面会谈到的，使用高斯函数的样本来构建加权平均滤波器。

第三种：设计具有规定频率响应的空间滤波器。例如Sobel算子那些。

5 空间域中的低通滤波器

平滑空间滤波器用于降低灰度的急剧过渡。由于随机噪声通常由灰度的急剧过渡造成，所以平滑的一个明显作用就是降噪。也可用于在图像重取样前平滑图像以减少混淆。

线性空间滤波是指图像与滤波器核进行卷积，一个平滑核与一幅图像的卷积会模糊图像，模糊程度取决于核的大小及其系数的值。

对于系数之和为1的核，用这些核对图像中恒定区域滤波时，滤波后的图像中这些区域也是恒定不变的，对于有急剧过渡的边缘和细节，则会起到平滑效果，防止了滤波过程中引入的偏差。可以与系数之和为0的核进行对比，系数之和为0的核主要用于检测边缘和细节，因为用这些核对图像中恒定区域滤波时，这个区域的滤波结果必为0，会将恒定区域显示为黑色背景，锐化滤波器会在6节中谈到。

5.1 盒式滤波器核

盒式滤波器核【均值滤波器】$$\frac{1}{9}\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right)$$

盒式滤波器核里面的系数都为1，前面有个归一化常数1/9。对该类滤波器进行归一化有以下2个目的：

1. 一个恒定灰度区域的灰度平均值将等于滤波后的图像中的灰度值；
2. 可防止在滤波过程中引入偏差。

也就是说，原图和滤波后的图像中，像素之和是相同的。

图3.33显示了这样一个例子。将盒式滤波器运用到图像中，可以观察到，核越大，图像的总体模糊程度就越大。由于在滤波前会对图像填充零，所以滤波后的图像会存在较细的灰色边框，因为填充零会扩展图像的边界。

2012甄题【名词解释】

图像平滑

图像平滑是指通过减少图像中的噪声和细节，使图像变得更为平滑和柔和的图像处理技术。常用的方法包括均值滤波、高斯滤波和中值滤波等，旨在提升图像质量并改善后续处理的效果。

2004甄题【计算题】

已知图像$f(x,y)=\left(\begin{array}{ccccccc}1& 0& 1& 0& 1& 0& 1\\ 2& 1& 2& 1& 2& 1& 2\\ 3& 2& 3& 2& 3& 2& 3\\ 4& 3& 4& 3& 4& 3& 4\\ 5& 4& 5& 4& 5& 4& 5\\ 6& 5& 6& 5& 6& 5& 6\\ 7& 6& 1& 6& 7& 6& 7\end{array}\right)$
（1）写出用$3\times 3$的均值滤波器模板处理后的图像（不处理边缘像素）；
（2）如果改成$5\times 5$或更大的模板处理，图像将变得怎样？
（3）均值滤波器与模板$\left(\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right)$的功能有何不同？

（1）$3\times 3$的均值滤波器模板为$$\frac{1}{9}\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right)$$，于是处理后的图像为$$\overline{f}(x,y)=\left(\begin{array}{ccccccc}1& 0& 1& 0& 1& 0& 1\\ 2& 15/9& 12/9& 15/9& 12/9& 15/9& 2\\ 3& 24/9& 21/9& 24/9& 21/9& 24/9& 3\\ 4& 33/9& 30/9& 33/9& 30/9& 33/9& 4\\ 5& 42/9& 39/9& 42/9& 39/9& 42/9& 5\\ 6& 51/9& 48/9& 51/9& 48/9& 51/9& 6\\ 7& 6& 7& 6& 7& 6& 7\end{array}\right)$$由于图像只有8个灰度级，故四舍五入后得到$\overline{f}(x,y)=\left(\begin{array}{ccccccc}1& 0& 1& 0& 1& 0& 1\\ 2& 2& 1& 2& 1& 2& 2\\ 3& 3& 2& 3& 2& 3& 3\\ 4& 4& 3& 4& 3& 4& 4\\ 5& 5& 4& 5& 4& 5& 5\\ 6& 6& 5& 6& 5& 6& 6\\ 7& 6& 1& 6& 7& 6& 7\end{array}\right)$

（2）模板越大，作用的像素范围越广，图像就会变得越平滑。
（3）均值滤波器是低通滤波器，其系数之和为1，主要用于平滑输入图像，模糊图像细节。而$\left(\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right)$是拉普拉斯核，为高通滤波器，其系数之和为0，主要用于增强图像细节。

2008、2012甄题【计算题】

$3\times 3$的算数均值滤波器模板为$$\frac{1}{9}\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right)$$于是处理后的图像为$$f=\frac{1}{9}\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 16& 25& 16& 0\\ 0& 25& 35& 19& 0\\ 0& 19& 23& 12& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$由于是8级图像，故四舍五入后得到结果图像：$f=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 2& 3& 2& 0\\ 0& 3& 4& 2& 0\\ 0& 2& 3& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right)$

2011、2014甄题【计算题】

（1）已知模板为$$M=\frac{1}{9}\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right)$$于是处理后的图像为$$\overline{I}=\frac{1}{9}\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 16& 25& 16& 0\\ 0& 25& 35& 19& 0\\ 0& 19& 23& 12& 0\\ 0& 0& 0& 0& 0\end{array}\right)$$由于是8级图像，故四舍五入后得到结果图像：$\overline{I}=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 2& 3& 2& 0\\ 0& 3& 4& 2& 0\\ 0& 2& 3& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right)$
（2）由于$M=\frac{1}{9}\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right)=\frac{1}{3}\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\cdot \frac{1}{3}\left(\begin{array}{ccc}1& 1& 1\end{array}\right)$，于是，$M$分离的两个一维模板分别是$\frac{1}{3}\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$和$\frac{1}{3}\left(\begin{array}{ccc}1& 1& 1\end{array}\right)$，分离处理可以提高计算速度。

课后习题3.26

(a) 在右侧图像中，黑白区域之间的边界点数量要多得多。当图像被模糊时，边界点会给右侧图像带来更多不同的值，因此两幅模糊图像的直方图也会不同。

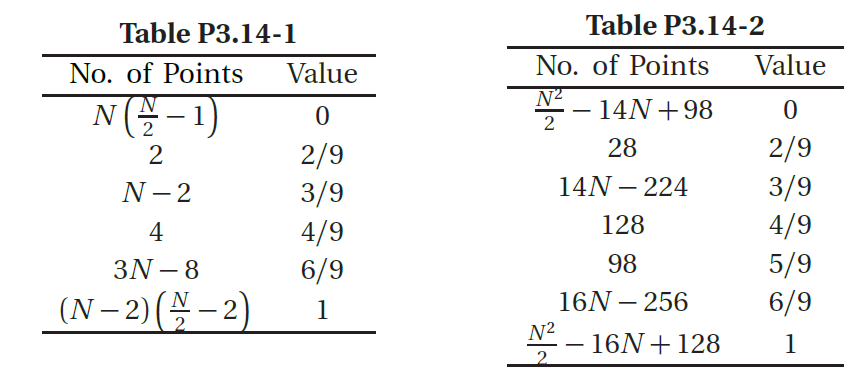
(b)为了处理边界效应，我们用 0 值边界包围图像。我们假设图像的大小为 $N\times N$（从问题陈述中的右侧图像中可以明显看出图像是正方形的）。模糊由系数为 $1/9$ 的 $3\times 3$ 模板实现。图 P3.14 显示了模糊的左侧图像将具有的不同类型的值（参阅问题陈述中的图像）。表P3.14-1汇总了这些值。很容易验证表格左列中的数字之和是 $N^2$。从此表中的条目可以很容易地构造直方图。类似的（繁琐的）过程在 Aable P3.14-2 中产生结果。

课后习题3.45

(a) 最极端的情况是，核被放置在一个 3 像素间隙的中心像素上，沿着一个较细的部分，在这种情况下，一个 $3\times 3$ 的核将包含一个完全空白的区域。由于这是已知的最大间隙，所以下一个（奇数）尺寸的核一定会包含该部分中的一些像素。因此，能满足要求的最小核是 $5\times 5$ 平均核。

(b)当模板覆盖的掩模区域中仅有两个像素时，模板产生的最小平均值。这个平均值是灰度值，不是像掩模区域中其余像素那样的二值像素。用$A_{min}$表示最小平均值，用 $B$ 表示掩模区域中的二值像素。显然$A_{min}<B$。然后，将二值化阈值设置为略小于$A_{min}$，将在模板的中心创建一个值为 $B$ 的二值像素。

课后习题3.34

从图 3.33 中我们知道，竖条宽 5 像素，高 100 像素，间隔为 20 像素。所讨论的现象与竖条之间的水平分离有关，因此我们可以通过考虑通过图像中竖条的单条扫描线来简化问题。回答这个问题的关键在于，一个竖条的开始和下一个竖条（比如说，在其右侧）的开始之间的距离（以像素为单位）是 25 像素。

考虑图P3.21所示的扫描线。图中还显示了 $25\times 25$模板 的横截面。模板的响应是它所包含的像素的平均值。我们注意到，当模板向右移动一个像素时，它会丢失左侧竖条的一个值，但它会在右侧拾取一个相同的值，因此响应不会改变。事实上，无论模板位于何处（只要它包含在竖条在内，而不是靠近竖条集的边缘），属于竖条且包含在模板中的像素数都不会改变。

还展示了一个$25\times 25$模板的横截面。模板的响应是它所传递的像素的平均值，我们注意到，当模板向右移动一个像素时，它会丢失左边垂直条的一个值，但它会在右边选择一个相同的像素，因此响应不会改变。事实上，属于垂直条并包含在模板中的像素数并没有改变，不考虑模板的位置(只要它包含在条形图中，而不是在一组条形图的边缘附近)。

模板下的竖条像素数没有变化的事实是由于竖条之间的特殊分离以及与模板的 25 像素宽度相关的线条宽度。这种恒定响应是问题陈述中显示的图像中看不到白色间隙的原因。请注意，$23\times 23$ 或 $45\times 45$ 模板不会发生这种恒定响应，因为它们与条形的宽度及其间隔不“同步”。

5.2 低通高斯滤波器核

高斯核是唯一可分离的圆对称核，表达式为$$w(s,t)=G(s,t)=K{e}^{-\frac{s^2+t^2}{2{\sigma }^2}}$$

图3.35a是一个高斯函数的透视图。

可分离性是圆对称高斯核的诸多基本性质之一。高斯函数的其他两个基本性质是：两个高斯函数的乘积和卷积也是高斯函数。

表3.6给出了两个一维高斯函数$f$和$g$的乘积和卷积的均值与标准差，由于高斯核的均值是零，所以我们感兴趣的是标准差。对于两个一维高斯函数$f$和$g$的乘积（×）和卷积（★）的标准差为$${\sigma }_{f\times g}=\sqrt{\frac{{\sigma }_f^2{\sigma }_g^2}{{\sigma }_f^2+{\sigma }_g^2}}$$ $${\sigma }_{f★g}=\sqrt{{\sigma }_f^2+{\sigma }_g^2}$$

图3.36显示了一个使用高斯核对图像进行低通滤波的例子。要生成21×21大小的高斯核，需要设置σ=3.5，因为6×3.5=21。与图3.33d中的21×21的盒式滤波器滤波的结果相比较，可以发现高斯滤波器的模糊程度明显降低，细节方面比使用同样大小的盒式滤波器保留的更清晰。当σ=7时，得到的结果就与图3.33d中的结果非常接近了。

图3.37说明了使用大于6σ×6σ的高斯核对图像是没有益的，对于同样标准差，但使用的高斯核大小不同的两幅图像滤波后的结果而言，他们的差值大小几乎可以忽略不计，如图3.37c所示，肉眼观察是一幅纯黑的图像。

比较图3.33d和图3.36c中的字母a可以发现，使用高斯核得到的边缘附近更平滑。图3.38清楚的显示了盒式核和高斯核之间的不同特性。

如图3.38b的剖面图所示，盒式核产生的是线性平滑，使得边缘处从黑色到白色的过渡呈现斜坡状，这是种硬过渡，希望边缘的平滑度较低时，通常用盒式滤波器。

观察图3.38c发现，高斯核会在边缘过渡周围产生更平滑的结果，希望产生均匀平滑结果时，通常使用高斯核滤波器。

前面提到过，对图像填充零会在滤波结果中引入黑色的边框，边框的宽度取决于所用滤波器核的大小和类型。为了消除这种黑色的边框，我们通常采用另外两种图像填充的方法：镜像填充和复制填充。

• 镜像填充：通过跨越边界镜像反射图像来得到边界以外的值。
• 复制填充：将边界之外的值设置为最接近的图像边界值。

当边界附近的区域包含图像细节时，镜像填充更适用；当图像边界附近的区域为常数时，复制填充更适用。

图3.39显示了三种填充方法的对比。可以发现，镜像填充和复制填充都没有恼人的黑色边框，效果看起来更好。

图3.40表明，给定大小的平滑核产生的相对模糊量直接取决于图像的大小。

图3.41显示了一个使用低通滤波和阈值处理提取感兴趣区域的例子。图3.41a是原图像，我们的目的是只想提取图中的4个主要明亮区域。图3.41b是使用高斯核滤波后的结构，图3.41c是使用阈值为$T=0.4$后得到的结果。阈值如何选取是第十章的内容。

导致图像阴影的主要原因之一是光照不均匀。图3.42显示了使用低通滤波矫正阴影的一个例子。

课后习题3.27【计算题】*

使用一个大小为 3×3、标准差为1.0的高斯核对一幅图像进行了4次滤波。由于卷积运算满足结合律，我们知道使用由各个核的卷积形成的单个高斯核能够得到同样的结果。
（a） 单个高斯核的大小是多少？
（b）标准差是多少？

（a）$Q=4，m=n=3$ 。根据公式 (3-39) 和 (3-40)，得单个高斯核的大小为$$[Q(m-1)+m]\times [Q(n-1)+n]=[4(3-1)+3]\times [4(3-1)+3]=11\times 11$$我们在第 5 小节中对高斯低通核的讨论可知，一个大小仅为 $3\sigma \times 3\sigma$ 的核将具有介于盒式核和高斯核之间的效果。我们需要 $6\sigma \times 6\sigma$大小的核才能获得具有平滑边缘的核的优势。

（b）由于由表3.6可得$\sigma =\sqrt{1^2+1^2+1^2+1^2}=2$

课后习题3.29*

讨论用一个$3\times 3$低通滤波器反复滤波一幅图像的极限效果。（可以忽略边界效应）

随着滤波次数的增加，每次滤波都会进一步去除细节，图像将变得越来越模糊。最终，所有细节信息都会被完全平滑掉，图像会趋近于一个均匀的灰色块，所有像素值逐渐相同，为整个图像的平均亮度。

总结：反复应用低通滤波器的极限效果是将图像平滑至全局均匀，没有细节的纯色图像。

直译答案：
研究空间滤波器重复应用的最简单方法之一就是使用叠加。令$f(x,y)$和$w$分别表述图像和滤波核。为方便起见，假设图像是大小为 $N\times N$，我们可以将 $f(x,y)$ 表示为最多 $N^2$ 个图像的总和，其中每个图像只有一个非零像素（最初，我们假设 $N$ 是无限的）。那么，使用核 $w$ 进行滤波的过程由以下卷积给出$$w★f=w★[f_1+f_2+...+f_{N^2}]$$为便于说明，假设 $f_i$ 的中心值为 1，而图像中的其他像素值为 0（见图 P3.29(a)）。 如果$w$是$3\times 3$大小值为$\frac{1}{9}$的核（图P3.29(b)），然后用 $w$ 对 $f_i$ 进行卷积将产生一幅图像，该图像是中心值为 $\frac{1}{9}$ 的 $3\times 3$ 阵列，其他位置值为 0，如图 $P3.29(c)$ 所示。如果现在将 $w$应用于这幅图像，得到的图像将如图 P3.39(d) 所示。请注意，图$P3.29(c)$和(d)中的非零像素之和是相同的，并且等于原始像素的值。因此，直观地看出，连续应用 $w$ 将 "扩散 "$f_i$ 的非零值（这并不是一个意料之外的结果，因为 $w$ 是一个模糊核）。由于和保持不变，非零元素的值将变得越来越小，随着滤波器的应用数量的增加。给出了所有卷积$f_k$相加的全部结果，$k=1,2,...,N^2$

每迭代模糊一次，数值就会从起点向外进一步扩散。在极限情况下，数值会变得无限小，但由于平均值保持不变，这就需要一个无限大小的图像。正是在这个交界处，边界条件变得重要。尽管问题陈述中没有要求，但在课堂上讨论对一幅有限大小的图像连续应用$w$的效果是有益的。最终的结果是，由于数值无法越过图像的边界向外扩散，连续应用平均化的分母最终会超过像素值，从而使图像在极限情况下归零。图 P3.29(e)给出了一个简单的例子，它显示了一个大小为 $1\times 7$ 的数组，通过连续应用 $1\times 3$ 的核 $w=[111]/3$ 进行模糊处理。我们可以看到，如果模糊的 1 的值可以扩散出去，得到的像素总和 $S$ 就是 1。然而，当遇到边界时，必须假设如何处理边界上的核运算。在这里，我们采用了一种常见的假设，即边界的像素值为 0。然而，核操作并没有超出边界。在这个例子中，我们看到像素值的总和开始随着连续应用核而减少。在极限情况下，$1/(3{)}^n$ 项将超过像素值之和，从而产生一个 0 的数组。

课后习题3.31【证明题】*

使用系数之和为1的一个核对图像进行滤波。证明原图像中的像素值之和，与滤波后的图像中的像素值之和相等。

我们假设进行全卷积操作，如公式（3-36）和（3-37）所述。设一般卷积核的系数为 $c_1,c_2,c_3,\dots ,c_k$。我们知道，在全卷积中，卷积核中的每个系数都会与输入图像中的每个像素进行一次乘法操作。执行的唯一操作是乘积求和。因此，如果我们展开卷积求和，累加所有项，并收集乘以原始图像中每个像素 $f(i,j)$ 的系数，我们会发现它们的表示形式如下：$$f(i,j)[c_1+c_2+\cdots +c_k]$$但是，假设所有系数的和为 1。因此，如果我们对图像中所有位置 $(i,j)$ 进行此操作并求和，我们可以得出结论：经过滤波后的图像中像素的总和将等于原始图像中像素的总和。

课后习题3.25

课后习题3.28

(a) 是。如表 3.6 所示，高斯的卷积就是高斯。
此外，正如我们在第 5 小节中对高斯低通核的讨论所知，若一个核的大小不在 $6\sigma \times 6\sigma$ 内，高斯核就不会有优势。本问题中的核的功能介于盒核和高斯核之间。

5.3 统计排序（非线性）滤波器【第五章还会详细介绍】

排序统计滤波器是非线性空间滤波器，主要包括中值滤波器、最大值滤波器和最小值滤波器。

• 中值滤波器用中心像素的邻域内的灰度值的中值替代中心像素的值，对于椒盐噪声尤其有效。中值滤波的功能是迫使各个点更像它们的邻点。

• 最大值滤波器使用邻域内的最大值来替代中心像素值，适用于处理胡椒噪声。

• 最小值滤波器使用邻域内的最小值来替代中心像素值，适用于处理盐粒噪声。

中值滤波器原理

1. 选择窗口：选定一个窗口大小，通常是一个奇数尺寸的矩形或正方形（例如 $3\times 3$, $5\times 5$）。
2. 窗口滑动：将该窗口从图像的左上角开始，逐步滑动到每个像素点。
3. 计算中位数：对于每个窗口，取出该窗口内所有像素的值，然后取这些值的中位数（即排序后中间的值）。
4. 替换值：用该中位数替换窗口中心的像素值。

假设有如下 $3\times 3$ 的图像矩阵，其中某些像素受到椒盐噪声影响，值为极端的 $0$ 或 $255$：

$$f=\left(\begin{array}{ccc}100& 150& 200\\ 0& 255& 100\\ 150& 200& 255\end{array}\right)$$

现在，我们使用一个 $3\times 3$ 的中值滤波器对这个图像进行处理。按照中值滤波器的步骤来进行操作：

1. 窗口的定义：使用 $3\times 3$ 窗口，即每次处理一个像素周围的 $3\times 3$ 区域。

2. 每个像素点的处理：

   • 对于中心像素（即 $f(2,2)=255$），考虑它的邻域：
     $$\left(\begin{array}{ccc}100& 150& 200\\ 0& 255& 100\\ 150& 200& 255\end{array}\right)$$
   • 排序该窗口中的像素值： { 0 , 100 , 100 , 150 , 150 , 200 , 200 , 255 , 255 } \{0, 100, 100, 150, 150, 200, 200, 255, 255\} {0,100,100,150,150,200,200,255,255}
   • 取中位数（第5个值）：$150$
   • 替换 $f(2,2)$ 为 $150$。

3. 继续处理其他像素：

   • 类似地，对于图像中的其他像素，按照相同的方式计算邻域中值并替换中心像素。

经过中值滤波器处理后的结果如下：

$$f_{\text{filtered}}=\left(\begin{array}{ccc}100& 150& 150\\ 150& 150& 150\\ 150& 200& 200\end{array}\right)$$

在这个例子中，中心像素 $f(2,2)=255$ 被替换为 $150$，并且其他受到噪声影响的像素也得到了平滑。

图3.43显示了中值滤波器对椒盐噪声处理的优势。

课后习题3.36*

(a) $n\times n$中值滤波器中有 $n^2$ 个点。因为 $n$ 为奇数，中值为$\zeta$，使得有 $(n^2-1)/2$ 个点的值$\le \zeta$，并且有相同数量的点的值$\ge \zeta$。然而，由于孤立像素族中的面积 $A$（点数）$<\frac{n^2}{2}$，且 $A$ 和 $n$ 均为整数， $A\le (n^2-1)/2$。因此，即使在极端情况下，即所有像素点都被滤波器包含在内，像素族中也没有足够的点等于中值（记住，我们假设所有像素点的颜色都高于或低于背景点）。因此，如果滤波器中的中心点是一个群集点，那么它将被设置为中值，然后从像素族中剔除。这一结论显然也适用于不太极端的情况，即中值滤波所包含的像素点数量小于像素族的最大规模。

(b)要使(a)中的结论成立，我们考虑的族像素(目标)点的数目不能超过$(n^2-1)/2$，因此，两个或多个不同的像素族不能足够接近，以便滤波器模板能包围来自多个像素族任意位置的像素点。由此可得，不同像素族中的任意两点之间的距离，不会小于模板的对角线长度减去一个像素单元的距离（该像素单元可以被其中一个像素族中的点占据）。假设像素间距为1个单位，则不同像素族的任意两点之间的最小距离必须大于$\sqrt{2}(n-1)$。换言之，这些点之间必须至少相隔 $n-1$ 个像素单元沿模板对角线跨越的距离。

课后习题3.37*

（a）对$n^2$个数进行排序，中值为排在第$\zeta =[n^2+1]/2$位的数。例如

1. 假设 $n=3$：则 $\zeta =[n^2+1]/2=5$。

2. 像素排序后：$[1,4,5,6,8,10,15,20,30]$。中值就是排在第5位的数：8

（b）在一次排序完成后，我们只需删除邻域尾部的值，并将邻域头部的值插入到已排序数组中的适当位置。