2025 全国大学生数学建模竞赛题目-B 题 碳化硅外延层厚度的确定 问题二完整思路
目标: 从给定的干涉光谱数据(波数 vs. 反射率)中,精确计算出外延层的厚度 d。
将非线性的干涉问题转化为一个线性回归问题,利用光谱中所有的干涉峰信息来求解厚度,从而提高结果的准确性和稳健性。
根据已知的文件:
(1)光谱数据文件(例如 附件1.xlsx),包含两列:波数 k (单位: cm⁻¹) 和 反射率 R (单位: %)。
(2)实验参数,即红外光的入射角 θ₁ (单位: 度)。
读取数据:
那么 我们从数据文件中读取波数和反射率数据,分别存入两个数组 k_raw 和 R_raw。
数据预处理:
由于: 原始光谱数据通常包含高频噪声,会干扰峰值的准确识别。平滑处理可以有效滤除这些噪声,使干涉条纹的主体轮廓更加清晰。 应用移动平均滤波器 (Moving Average Filter)。该方法将数据序列中的每一个点替换为其邻近若干个点的平均值,R_smooth = smooth(R_raw, window_size)。
参数选择: window_size (窗口大小) 是一个关键参数。如果太小,去噪效果不明显如果太大,会过度平滑,导致干涉峰变钝甚至幅度减小,影响峰值定位精度。经验建议: 对于给定的数据,选择一个介于 10到20个数据点之间的窗口大小通常效果很好。
准确地找到所有由相长干涉(亮条纹)引起的反射率极大值点。
使用一个标准的寻峰算法(如 MATLAB 的 findpeaks 函数)在平滑后的数据 R_smooth 上进行操作。pks_wavenumber = findpeaks(R_smooth, k_raw, parameters...)
关键参数设置:MinPeakProminence' (最小峰突 prominence): 这是最重要的参数。它定义了一个峰值必须比其两侧的“山谷”高出多少才被认为是一个有效的峰。
作用: 有效地滤除由噪声引起的虚假小峰。设置方法: 观察平滑后的光谱图,估算一个有效干涉峰相对于其基线的典型高度。
例如,如果干涉条纹的振幅大约在 10% 左右,可以将此参数设置为 1 或 2,以确保所有真实峰都能被检测到。MinPeakDistance' (最小峰间距): 定义了两个相邻峰值在波数轴上的最小间隔。防止在同一个宽峰的顶部或肩部识别出多个峰。
观察光谱图,估算两个相邻干涉峰之间的大致波数距离,并设置一个略小于此距离的值。经过此步骤,我们得到一个包含 N 个峰值波数的一维数组,记为 k_peaks = [k₁, k₂, ..., k_N]。
相长干涉条件为 2 * n₁ * d * cos(θ₂) = m * λ,
其中 m 是一个整数,称为干涉级数。 将公式中的波长 λ 转换为波数 k (因为我们的数据是以波数为单位的)。它们的关系是 λ = 1/k。代入后得到:2 * n₁ * d * cos(θ₂) = m / k。
方程重排: 将上式整理,以 m 作为因变量:
m = (2 * n₁ * d * cos(θ₂)) * k
这个方程揭示了一个核心关系:干涉级数 m 与波数 k 呈正比。
引入相对干涉级数 j: 我们不知道每个峰值 k_i 对应的绝对干涉级数 m_i(例如,它可能是从 m=50 开始的序列)。但是,我们知道它们是连续的整数。因此,我们可以定义一个相对干涉级数 j,它从0开始计数:
对于第一个峰 k₁,j₁ = 0
对于第二个峰 k₂,j₂ = 1
...
对于第 N 个峰 k_N,j_N = N-1
这样,我们就有了一个数组 j = [0, 1, 2, ..., N-1]。
建立线性方程: 绝对级数 m 和相对级数 j 的关系是 m = j + m₀,其中 m₀ 是第一个峰对应的未知整数常数
。
将此关系代入步骤3的方程中:
j + m₀ = (2 * n₁ * d * cos(θ₂)) * k
整理成标准的线性方程 y = a*x + b 形式:
j = (2 * n₁ * d * cos(θ₂)) * k - m₀
模型对应关系:
y <==> 相对干涉级数 j
x <==> 峰值波数 k_peaks
斜率 a (Slope) <==> 2 * n₁ * d * cos(θ₂)
截距 b (Intercept) <==> -m₀
执行拟合:
使用最小二乘法对我们准备好的数据点 (k_peaks, j) 进行线性回归拟合。
输出: 得到拟合直线的斜率 Slope 和截距 Intercept。
计算 cos(θ₂):
根据斯涅尔定律 n₀ * sin(θ₁) = n₁ * sin(θ₂) 和三角恒等式 cos²(θ₂) + sin²(θ₂) = 1,可以推导出:
cos(θ₂) = √(1 - (n₀/n₁ * sin(θ₁))²)
所需参数:
n₀: 入射介质的折射率,通常是空气,n₀ = 1。
n₁: 外延层的折射率。这是一个关键的物理参数,需要根据材料(本例中是4H-SiC)和测量波段来确定。在此红外波段,n₁ ≈ 2.56 是一个合理的近似值。
θ₁: 已知的入射角。
求解厚度 d:
从步骤3我们知道 Slope = 2 * n₁ * d * cos(θ₂)。
将此方程重排以求解 d:
d = Slope / (2 * n₁ * cos(θ₂))
单位换算 (至关重要):
由于波数 k 的单位是 cm⁻¹,而 j 是无量纲的,因此计算出的斜率 Slope 的单位是 cm。
所以,上一步计算出的厚度 d 的单位也是 cm。
通常厚度的标准单位是微米 (μm)。执行单位换算:
d_μm = d_cm * 10000
计算决定系数 R² (R-squared):
对线性拟合的结果计算 R² 值。这个值介于0和1之间,衡量了数据点与拟合直线的贴合程度。
解读:
R² 越接近1,说明线性关系越强,数据质量越高,模型越适用,计算结果越可靠。
对于本问题,一个好的结果其 R² 值应该非常高(例如 > 0.999)。
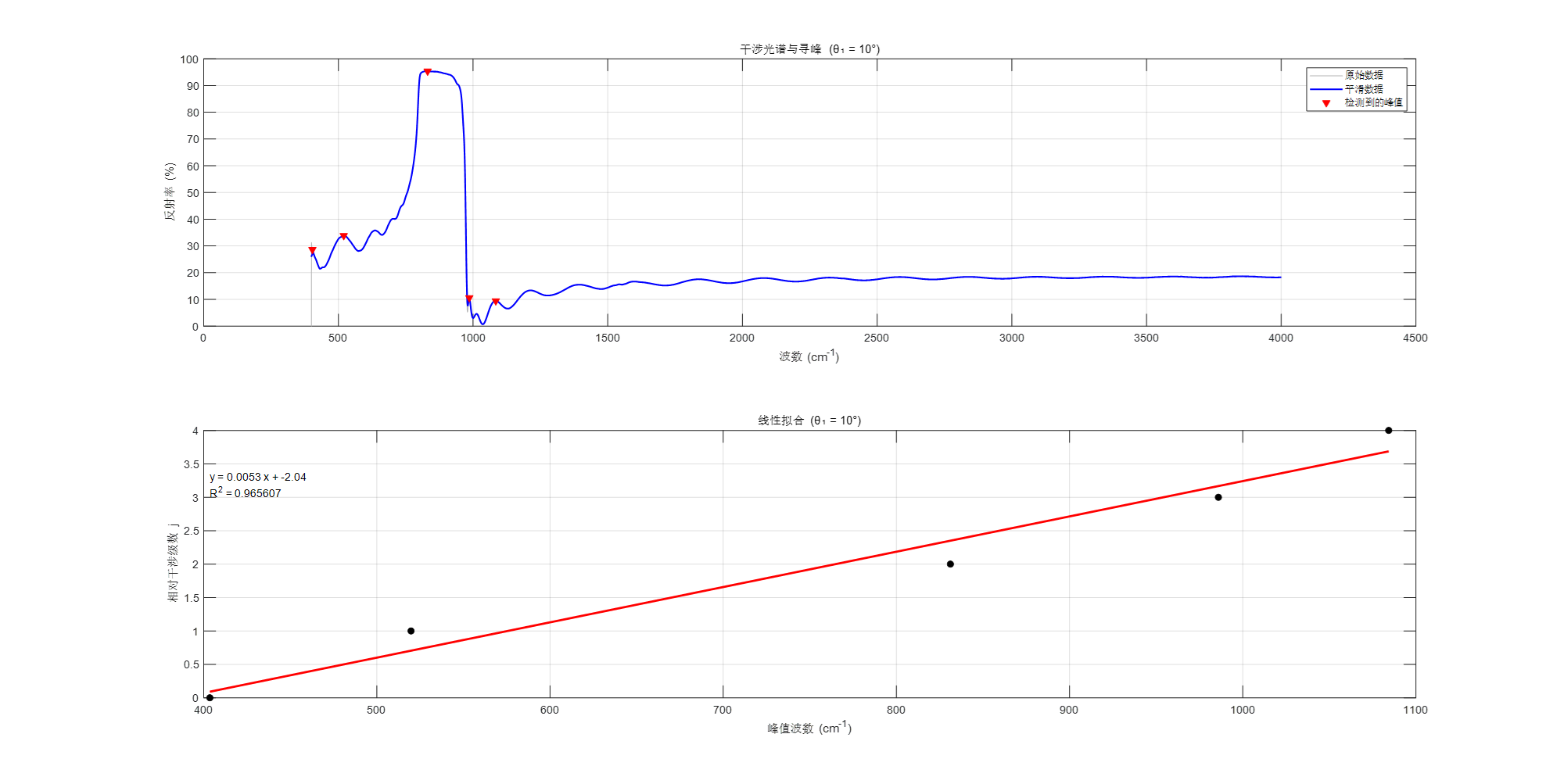
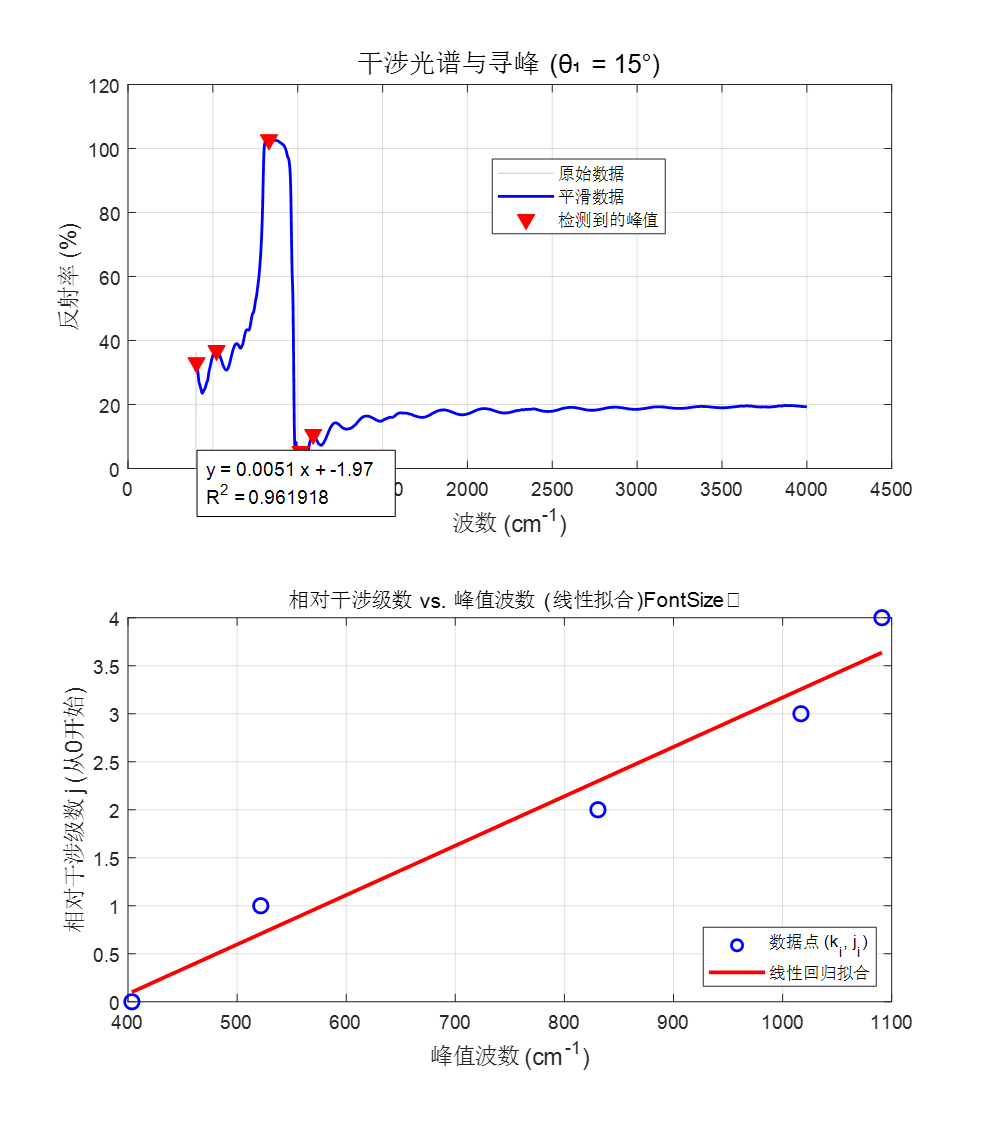
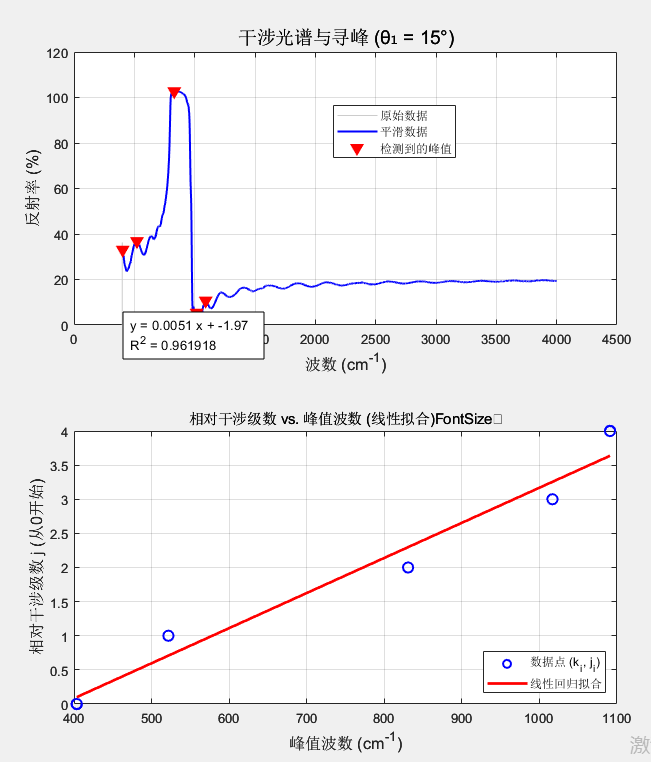
可视化:
绘制两张图来进行视觉检查:
图一: 原始光谱、平滑后光谱以及标记出的峰值点。用于检查寻峰步骤是否准确。
图二: (k_peaks, j) 散点图以及线性回归拟合的直线。用于直观判断线性模型的拟合优度。