当前位置： 首页 > ds >正文

矩阵指数函数 e^A

ds 2025/7/31 8:18:36

在数学和量子物理中，以自然常数 e 为底、指数部分包含矩阵的泰勒级数展开，是描述矩阵指数函数 e^{A} （其中 A 是一个方阵）的核心工具。

 

1. 矩阵指数的泰勒级数定义

对于任意 n \times n 矩阵 A，其指数函数 e^{A} 定义为以下泰勒级数：

        e^{A} = \sum_{k=0}^{\infty} \frac{A^k}{k!} = I + A + \frac{A^2}{2!} + \frac{A^3}{3!} + \cdots

其中：

    A^k 是矩阵 A 的 k 次幂（A^0 = I，I 为单位矩阵。

    级数对任意有限维矩阵 A 均收敛（因为 \|A^k\| / k! 随  k  增长趋于零）。

 

2. 关键性质

（1）收敛性

    矩阵指数的泰勒级数绝对收敛，对任何 A 均有定义。

    收敛速度取决于 A 的范数 \|A\|。

（2）指数乘法公式

    若矩阵 A 和 B 可交换（即 AB = BA），则：

            e^{A+B} = e^{A} e^{B}

    否则需使用Lie-Trotter公式近似：

            e^{A+B} = \lim_{n \to \infty} \left( e^{A/n} e^{B/n} \right)^n

（3）导数与微分方程

   矩阵指数是线性微分方程的解：

            \frac{d}{dt} e^{tA} = A e^{tA}, \quad e^{0A} = I

    这在量子力学中对应薛定谔方程   \frac{d}{dt} |\psi(t)\rangle = -iH |\psi(t)\rangle  的解  |\psi(t)\rangle = e^{-iHt} |\psi(0)\rangle 。

 

3. 计算矩阵指数的具体方法

方法1：对角化法（若 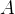A 可对角化）

    若 A 可表示为 A = PDP^{-1} ，其中  D = \text{diag}(\lambda_1, \lambda_2, \dots) ，则：

            e^{A} = P e^{D} P^{-1}, \quad e^{D} = \text{diag}(e^{\lambda_1}, e^{\lambda_2}, \dots)

示例：
设  

            A = \begin{pmatrix} 2 & 1 \\ 0 & 3 \end{pmatrix} 

    其特征值为 \lambda_1=2、\lambda_2=3 

    对角化后：

            e^{A} = P \begin{pmatrix} e^{2} & 0 \\ 0 & e^{3} \end{pmatrix} P^{-1} 

方法2：幂级数截断（数值计算）

    对无法对角化的矩阵，截断泰勒级数前 N 项：

          e^{A} \approx \sum_{k=0}^{N} \frac{A^k}{k!} ​

    需根据精度要求选择 N。

方法3：利用Jordan标准形

    若 A 不可对角化，可化为 Jordan 块  J，再计算 e^{J}。
对Jordan块 J = \lambda I + N （N 为幂零矩阵）：

           e^{J} = e^{\lambda} \sum_{k=0}^{m-1} \frac{N^k}{k!} ​

 

4. 量子力学中的特例：幺正演化

在量子系统中，哈密顿量 H 是厄米矩阵（H^\dagger = H），时间演化算符为：

            U(t) = e^{-iHt / \hbar}

    泰勒展开：

        U(t) = I - \frac{iHt}{\hbar} - \frac{H^2 t^2}{2\hbar^2} + \frac{iH^3 t^3}{6\hbar^3} + \cdots

    物理意义：
每一项 H^k 代表不同阶的量子相互作用，级数收敛保证幺正性。

 

5. 示例：Pauli矩阵的指数

    对Pauli矩阵

             \sigma_x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}

        计算 e^{i\theta \sigma_x}​：

  1. 对角化：
    \sigma_x​ 的特征值为 \pm 1，对角化为   \sigma_x = P \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} P^{-1} 

  2. 指数计算：

    e^{i\theta \sigma_x} = P \begin{pmatrix} e^{i\theta} & 0 \\ 0 & e^{-i\theta} \end{pmatrix} P^{-1} = \cos(\theta)I + i\sin(\theta)\sigma_x 

  3. 结果：

    e^{i\theta \sigma_x} = \begin{pmatrix} \cos\theta & i\sin\theta \\ i\sin\theta & \cos\theta \end{pmatrix} 

    此为量子比特的 X轴旋转门 R_x(\theta) 。

 

6. 泰勒级数的局限性及替代方法

高维矩阵：泰勒级数收敛可能较慢，需大量项才能精确。

替代方案：

        Padé近似：有理分式逼近，加速收敛。

        Krylov子空间法：适用于稀疏矩阵。

        量子线路模拟：在量子计算机上直接实现 e^{iA}（如 Trotter 分解）。

 

7.总结一下

    矩阵指数 e^{A} 的泰勒级数是理解量子演化、线性系统和控制理论的基础。量子计算中，幺正演化 e^{-iHt} 的展开直接对应量子门的实现（如旋转门、哈密顿模拟）。计算技巧方面，对角化法适用于可对角化矩阵，而数值方法（如级数截断）处理一般情况。通过泰勒级数，矩阵指数将抽象的线性算子与具体的物理操作（如量子门）联系起来，成为量子理论与计算的核心数学工具。

http://www.xdnf.cn/news/16784.html

相关文章：

  • 移动管家手机控车系统硬件安装与软件绑定设置
  • LeetCode 4：寻找两个正序数组的中位数
  • DISTILLM：迈向大型语言模型的简化蒸馏方法
  • 基于React+Express的前后端分离的个人相册管理系统
  • OpenBayes 一周速览丨Self Forcing 实现亚秒级延迟实时流视频生成；边缘AI新秀，LFM2-1.2B采用创新性架构超越传统模型
  • 爱车生活汽车GPS定位器：智能监控与安全驾驶的守护者
  • 云原生环境里的显示变革：Docker虚拟浏览器与cpolar穿透技术实战
  • 新零售“实—虚—合”逻辑下的技术赋能与模式革新：基于开源AI大模型、AI智能名片与S2B2C商城小程序源码的研究
  • RAG：检索增强生成的范式演进、技术突破与前沿挑战
  • pytorch入门2：利用pytorch进行概率预测
  • 智慧城市SaaS平台|市政公用管理系统
  • LeetCode Hot 100 搜索旋转排序数组
  • Java项目：基于SSM框架实现的济南旅游网站管理系统【ssm+B/S架构+源码+数据库+毕业论文+远程部署】
  • Linux系统指令之 —— passwd
  • 【maven】仓库配置
  • 基于 Hadoop 生态圈的数据仓库实践 —— OLAP 与数据可视化（二）
  • 15.10 单机8卡到千卡集群！DeepSpeed实战调参手册：A100训练效率翻倍，百万成本优化实录
  • 【C++详解】深入解析多态 虚函数、虚函数重写、纯虚函数和抽象类、多态原理、重载/重写/隐藏的对⽐
  • composer 常用命令
  • Unity_XR控制手部动画
  • NVIDIA Isaac平台推动医疗AI机器人发展研究
  • C++：STL中list的使用和模拟实现
  • 常见的cms框架的webshell方法
  • JavaScript和小程序写水印的方法示例
  • 谈谈毕业工作一年后的变化
  • 【C语言】指针深度剖析（一）
  • 集成电路学习：什么是Wi-Fi无线保真度
  • Java优雅使用Spring Boot+MQTT推送与订阅
  • 使用LangChain构建法庭预定智能体：结合vLLM部署的Qwen3-32B模型
  • Accessibility Insights for Windows 使用教程