DISTILLM：迈向大型语言模型的简化蒸馏方法

温馨提示：
本篇文章已同步至"AI专题精讲" DISTILLM：迈向大型语言模型的简化蒸馏方法

摘要

知识蒸馏（Knowledge Distillation, KD）被广泛用于将教师模型压缩为更小的学生模型，从而在保留模型能力的同时降低推理成本和内存占用。然而，当前面向自回归序列模型（如大型语言模型）的知识蒸馏方法缺乏统一的目标函数。此外，近年来为解决训练与推理之间的不一致性而使用学生模型生成的输出，极大地增加了计算开销。

为了解决这些问题，我们提出 DISTILLM，一个面向自回归语言模型的更高效且更有效的知识蒸馏框架。DISTILLM 包括两个组成部分：（1）一种新颖的偏斜 Kullback-Leibler 散度（skew KLD）损失函数，我们揭示并利用了其理论属性；（2）一种自适应的 off-policy 策略，旨在提高使用学生生成输出的效率。

我们在多个实验中（包括指令跟随任务）验证了 DISTILLM 的有效性，证明它能够构建性能强大的学生模型，并在与当前主流蒸馏方法的对比中，实现高达4.3 倍的训练加速。

1. 引言

近年来，自回归语言模型（LM，例如 OpenAI, 2023；Touvron 等，2023）尤其是大型语言模型（LLM）的快速发展，显著提升了文本生成任务（如通用指令跟随任务）的质量（Wang 等，2023b）。这一成功通常归因于训练数据和模型参数规模的扩大（例如 GPT-3 拥有 175B 参数；Brown 等，2020）。然而，增加参数量也带来了相应的成本，使得由于推理开销高或内存占用大而限制了这些模型的部署。因此，将这些高容量模型压缩，在尽可能保留其性能的前提下减少参数数量，成为其实际应用的关键目标。

随着对计算资源需求的降低变得愈发重要，**知识蒸馏（KD，Hinton 等，2015）**成为一种极具潜力的方法。该方法通过将大容量的教师模型（如 LLM）中的知识迁移到更小的学生模型，实现压缩。大多数 KD 方法采用了 Kullback-Leibler 散度（KLD）损失，要求学生模型在固定数据集上生成与教师模型一致的输出（Kim & Rush, 2016；Sanh 等，2019）。这些方法显著提升了学生模型的性能，使其在效率提升的同时具备与教师模型相近的能力，尤其适用于各种分类任务（Sun 等，2019；Mirzadeh 等，2020）。

然而，基于固定数据集使用 KLD 的方法，在应用于自回归语言模型时存在两个主要问题：

• 问题一：KLD 带来的不理想效果。生成任务相比分类任务更为复杂，使用 KLD 可能导致学生分布过于平滑，无法充分拟合教师分布，或反之在高概率区域发生过度集中。这种现象被称为模式平均（mode averaging）或模式崩溃（mode collapse），其根源在于 KLD 的不对称性（Wen 等，2023；Gu 等，2024）。

• 问题二：训练-推理分布不匹配。在训练阶段使用固定数据集，会导致训练时观察到的序列与学生在自回归推理中生成的序列分布不一致，产生所谓的曝光偏差（exposure bias）问题（Arora 等，2022）。

近期已有研究尝试通过引入其他散度损失函数（Wen 等，2023；Agarwal 等，2024）或使用学生生成输出（SGO，Lin 等，2020；Agarwal 等，2024）来应对上述问题。然而，这些方法通常缺乏统一的目标函数，且由于不断生成 SGO 而效率低下。例如，Agarwal 等（2024）使用基于策略的蒸馏方式引入 SGO，但其样本效率低下、生成时间较长，因为训练过程中需要频繁地提示学生生成新的训练序列。此外，他们的实验表明最优的散度函数可能是任务相关的，这使得寻找合适的损失函数变得繁琐。

Gu 等（2024）引入了一种策略优化方法，用于最小化学生与教师分布之间的反向 KLD，但该方法要求在每次迭代中对两个模型同时进行生成，从而影响了训练效率。

贡献

在本文中，我们提出了 DISTILLM，它包含一种新颖的偏斜 KLD 损失函数和一种自适应的 off-policy 策略，兼顾蒸馏效果和训练效率。我们在理论和实证层面均验证了 DISTILLM 各组件的有效性及其协同作用。具体贡献如下：

• 偏斜 KLD（Skew KLD）：我们关注当前目标函数存在的两个关键问题：优化 KLD 损失时可能出现的梯度爆炸导致的不稳定性，以及缺乏对泛化能力和收敛性的强调。为此我们引入了 偏斜 KLD，这是一种具有良好理论基础的新型目标函数，旨在优化稳定梯度、最小化近似误差，在实验中表现出更快的收敛速度和更优的性能。

• 自适应 off-policy 策略：虽然在 KD 中使用 SGO 通常有助于提升性能，但它显著增加了训练时间（见图2），并且难以确定最优的 SGO 使用比例。为此，我们提出了一种自适应的 off-policy 模块，能够更高效且有选择性地利用 SGO，从数据角度改进 KD 效率。

• 优异的性能与效率：DISTILLM 在多种生成类任务（如指令跟随、文本摘要）中达到了当前最先进的学生模型性能，并相较于近期 KD 方法（Gu 等，2024；Agarwal 等，2024）实现了 2.5∼4.3× 的训练加速。

2. 背景

2.1 用于自回归生成语言模型的知识蒸馏

我们提供用于自回归生成语言模型的知识蒸馏（KD）的基础信息。给定一个源序列和目标序列对，记作 $(x,y)$，KD 最小化固定教师模型 $p(y|x)$ 与参数化学生模型 $q_{\theta }(y|x)$ 分布之间的散度 $D$。训练数据对 $(x,y)$ 要么从固定的真实数据集中采样（Hinton et al., 2015），要么来自教师生成的输出（Kim & Rush, 2016）。

传统上，由于其简单性和易于计算，Kullback-Leibler 散度（KLD），记作 $D_{\text{KL}}$，是 KD 中最常用的损失函数。使用 KLD 进行的序列级蒸馏可以准确地分解为 token 级的蒸馏之和：
$$\begin{array}{r}{D}_{\mathrm{KL}}(p,q_{\theta })={\mathbb{E}}_{\mathbf{x}}{\mathbb{E}}_{\mathbf{y}\sim p(\cdot |\mathbf{x})}\left[\log \frac{p(\mathbf{y}|\mathbf{x})}{q_{\theta }(\mathbf{y}|\mathbf{x})}\right]\end{array}(1)$$

$$\begin{array}{r}\approx \frac{1}{|\mathcal{D}|}{\sum }_{(\mathbf{x},\mathbf{y})\in \mathcal{D}}p(\mathbf{y}|\mathbf{x})\log \frac{p(\mathbf{y}|\mathbf{x})}{q_{\theta }(\mathbf{y}|\mathbf{x})}\end{array}(2)$$

$$\begin{array}{r}=\frac{1}{|\mathcal{D}|}{\sum }_{\mathbf{x}\in {\mathcal{D}}_X}{\sum }_t^{|\mathbf{y}|}{\sum }_{y_t\in V}p(y_t|{\mathbf{y}}_{<t},\mathbf{x})\log \frac{p(y_t|{\mathbf{y}}_{<t},\mathbf{x})}{q_{\theta }(y_t|{\mathbf{y}}_{<t},\mathbf{x})}\end{array}(3)$$

其中 $V$ 是词汇 token 集合，$y_{<t}:=(y_1,y_2,\dots ,y_{t-1})$ 表示直到索引 $t-1$ 的 token 序列。我们仅关注可解的 KLD，因为其他散度（例如总变差距离 TVD，Wen et al., 2023）无法有效地将序列级蒸馏分解为 token 级组成部分。虽然 KLD 的显式定义在公式 (1) 中给出（Kim & Rush, 2016；Wen et al., 2023），但大多数近期研究（如 Agarwal et al., 2024；Gu et al., 2024）在假设教师分布与其训练数据集 $\mathcal{D}$ 相似的前提下，通过最小化公式 (2) 来近似进行分布匹配。为了提高训练效率，我们的方法在训练时使用公式 (2) 的定义，而公式 (1) 用于第 1 条定理中对我们提出的蒸馏目标进行理论分析。

2.2. 现有蒸馏方法的陷阱

目标函数的局限性。
KD 中的 KLD 目标函数由于其不对称性（Wen 等人，2023），常常迫使学生模型的分布覆盖教师模型分布的整个支持集，从而带来显著的限制。当一个采样的数据点包含在教师分布的支持集中但不在学生分布中时，这一问题尤为明显，即存在某个 $(x,y)$ 满足 $p(y|x)\gg 0$ 且 $q_{\theta }(y|x)\approx 0$。如果学生模型无法具备匹配教师分布所有支持集的能力，这种局限性将更加突出。因此，这会导致学生模型出现模态平均（mode-averaging）问题，即为了试图覆盖教师分布的全部支持集而学习到过于平滑的分布，正如近期的研究所指出的那样（Wen 等人，2023；Gu 等人，2024）。

一些最新研究部分地通过应用反向 KLD（RKLD，Gu 等人，2024；Agarwal 等人，2024）来缓解这一问题，RKLD 定义为 $D_{\mathrm{RKL}}(p,q_{\theta }):=D_{\mathrm{KL}}(q_{\theta },p)$；或通过引入插值参数 $\beta \in [0,1]$ 的广义 JSD（Agarwal 等人，2024），其定义如下：
$$\begin{array}{rl}& D_{\mathrm{JSD}}^{(\beta )}(p,q_{\theta }):=\beta D_{\mathrm{KL}}(p,\beta p+(1-\beta )q_{\theta })\\ & +\left(1-\beta \right)D_{\mathrm{KL}}(q_{\theta },\beta p+(1-\beta )q_{\theta })\end{array}(4)$$
这些方法在自回归语言模型中表现出了一定的经验性成功，但仍需要系统性的研究，以提供一个建立在全面的理论与实证分析基础上的标准蒸馏目标函数。由于这些近期提出的目标函数缺乏这样的理论支持，导致其性能表现次优且在不同任务中存在不稳定性（Agarwal 等人，2024）。

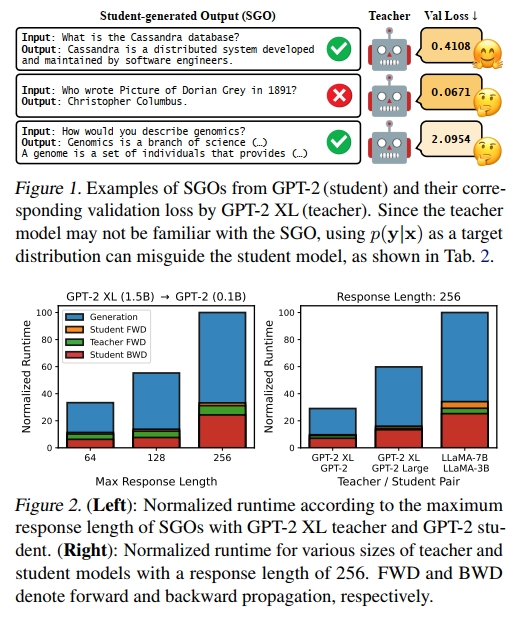
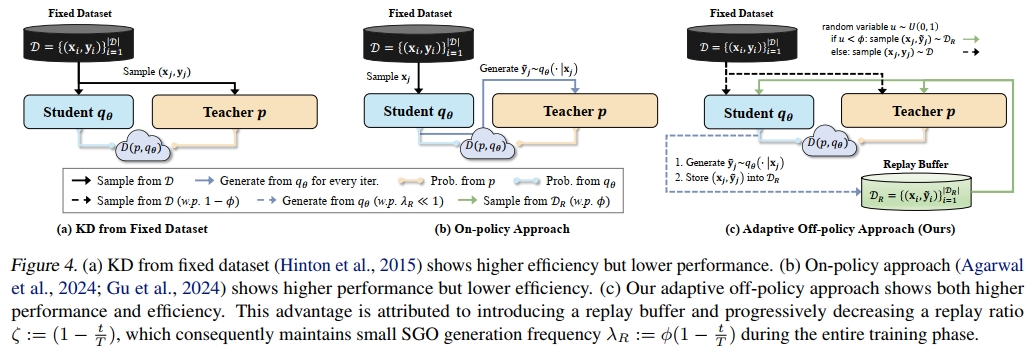
使用 SGO 的局限性。此前用于自回归语言模型的知识蒸馏方法，在训练过程中使用固定数据集样本，而在推理过程中使用学生模型生成的样本，两者之间存在训练-推理不匹配问题。近期研究（Lin 等人，2020；Agarwal 等人，2024）尝试通过引导学生模型生成 SGO（Student-Generated Outputs），再使用教师模型对这些序列的反馈进行训练，从而缓解这一问题。这种方法通过让学生模型在其熟悉的自生成序列上进行训练，有效地缓解了分布不匹配问题，并显著提升了对大型语言模型的蒸馏效果（Lin 等人，2020；Agarwal 等人，2024）。

尽管此方法在性能上有效，但我们指出当前对 SGO 的使用仍存在两个主要问题。首先，教师模型在面对训练数据分布之外的、不准确的 SGO 时，可能会出现分布不匹配，进而对学生模型 qθq_\theta 产生误导。如图 1 所示，这种分布不一致可能导致教师模型对不正确但较短的生成给予较低验证损失，而对较长但正确的生成给予较高验证损失。其次，如图 2 所示，在每轮迭代中都生成 SGO 的做法计算效率低下。在所有实验中，无论 SGO 的最大序列长度（64 至 256）或模型规模（从 GPT-2 到 OpenLLaMA2-3B），SGO 的生成都占据了总训练时间的相当大一部分，最高可达 80%。

然而，据我们所知，尚未有方法能够同时系统性地解决上述挑战。例如，MiniLLM（Gu 等人，2024）提出了一种混合教师模型与学生模型分布的方法，以缓解第一个问题。然而，该方法由于需要使用大型教师模型，显著增加了训练计算成本。这些挑战促使我们开发一种新方法，能够自适应地平衡训练-推理不匹配减少所带来的正面效果（Agarwal 等人，2024）与教师模型噪声反馈导致性能下降的负面影响（如表 2 所示）。与此同时，我们还旨在提升 SGO 的样本效率，从而提高整体的计算效率。

3. DISTILLM

本节我们将介绍 DISTILLM 的技术细节，旨在解决以往方法的局限性。我们提出的方法包括：(1) Skew KLD（第 3.1 节），该方法显著提升了优化稳定性和泛化能力。Skew KLD 损失解决了以往目标函数存在的陷阱，这些陷阱可能导致学生模型陷入缺乏理论基础的次优解；(2) 自适应离策略方法（第 3.2 节），该方法包含一种新颖的自适应 SGO 调度器，通过最小化对 SGO 的使用，在噪声反馈与训练-推理不匹配之间取得平衡，并利用离策略策略提升 SGO 的样本效率，同时保持模型性能。我们在算法 1 中展示了 DISTILLM 的整体流程。

3.1. Skew（反向）KLD

我们从数学角度出发，提出了将 KLD 扭曲（skew）后在优化过程中更有利于学生模型性能提升的动机。Skew KLD（SKL，Lee，2001）的定义引入了参数 $\alpha$，用于控制两个分布的混合比例。α-SKL 在分布 $p$ 与 $q_{\theta }$ 之间被定义为 $p$ 与混合分布$\alpha p+(1-\alpha )q\theta$ 之间的 KLD：
$$D_{\mathrm{SKL}}^{(\alpha )}(p,q_{\theta })=D_{\mathrm{KL}}\left(p,\alpha p+(1-\alpha )q_{\theta }\right)$$
我们同样定义了 α-SRKL 为

$$D_{\text{SRKL}}^{(\alpha )}(p,q_{\theta })=D_{KL}(q_{\theta },(1-\alpha )p+\alpha q_{\theta }).$$

基于我们详尽的分析，我们提出一个全面的见解，认为 S®KL 相较于其他损失函数更优越，原因在于它具有更稳定的梯度和更小的近似误差。

稳定的梯度
为了实现对 SKL 的稳定优化，我们首先分析了 KLD 和 SKL 对参数 $\theta$ 的梯度。给定一个上下文-目标序列对 $(x,y)$，我们定义 KLD 关于 $\theta$ 的梯度（Ji 等，2023）：
$${\nabla }_{\mathbf{\theta }}{D}_{\mathrm{KL}}(p,q_{\mathbf{\theta }})=-{\mathbf{r}}_{p,q_{\mathbf{\theta }}}{\nabla }_{\mathbf{\theta }}{q}_{\mathbf{\theta }}(\mathbf{y}|\mathbf{x})(5)$$
其中 $r_{p_1,p_2}$ 是任意两个分布 $p_1$ 和 $p_2$ 之间的比值。结果是模型概率的负梯度，其权重与该概率值成反比。如果 $q_{\theta }(y|x)\approx 0$，则梯度的范数会变得很大，导致参数更新步长显著且可能带来噪声。这些因素可能对梯度更新产生负面影响，从而影响优化过程。接下来，我们计算 SKL 关于 $\theta$ 的梯度：
$${\nabla }_{\theta }{D}_{\mathrm{SKL}}^{(\alpha )}(p,q\theta )=-\underset{\mathrm{coefficient}}{\underbrace{(1-\alpha ){\mathbf{r}}_{p,{\tilde{q}}_{\theta }}}}{\nabla }_{\theta }{q}_{\theta }(\mathbf{y}|\mathbf{x})(6)$$
其中 ${\tilde{q}}_{\theta }(y|x)=\alpha p(y|x)+(1-\alpha )q_{\theta }(y|x)$。相比于 KLD，SKL 由于对 $p$ 和 $q_{\theta }$ 的插值，避免了 $r_{p,{\tilde{q}}_{\theta }}$ 分母接近零，从而减小了梯度范数。这使得 SKL 的梯度更加稳定。对 RKLD 和 SRKL 的梯度分析也显示出类似的趋势。
$$\begin{array}{rlr}& & {\nabla }_{\theta }{D}_{\mathrm{KL}}(q_{\theta },p)=-\left(\log {\mathbf{r}}_{q_{\theta },p}+1\right){\nabla }_{\theta }{q}_{\theta }(\mathbf{y}|\mathbf{x}),(7)\\ & & {\nabla }_{\theta }{D}_{\mathrm{SKL}}^{(\alpha )}(q_{\theta },p)=-\underset{\mathrm{coefficient}}{\underbrace{\left(\log {\mathbf{r}}_{q_{\theta },\tilde{p}}+1-\alpha {\mathbf{r}}_{q_{\theta },\tilde{p}}\right)}}{\nabla }_{\theta }{q}_{\theta }(\mathbf{y}|\mathbf{x}),\end{array}$$
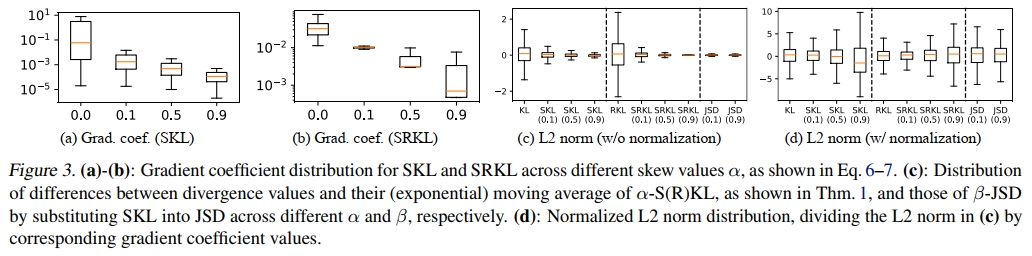
其中 $\tilde{p}(y|x)=(1-\alpha )p(y|x)+\alpha q_{\theta }(y|x)$。所有梯度推导详见附录 B.1。我们在图 3(a) 和图 3(b) 中对梯度系数分布进行了可视化，验证了我们的梯度分析。随着 $\alpha$ 增大，SKL 和 SRKL 的系数都显著减小。

较小的近似误差：我们证明了来自小批量训练的 SKL 经验估计器具有有界的 $L_2$ 范数。该有界范数保证了快速收敛，且估计器与真实散度之间误差最小，从而通过准确反映整体分布，实现高泛化能力。

定理1. 设 $p_n^1$ 和 $p_n^2$ 分别为从分布 $p^1$ 和 $p^2$ 独立同分布抽取的 $n$ 个样本的经验分布。在温和假设下，α-SKL 估计量 $D_{SKL}^{(\alpha )}(p_n^1,p_n^2)$ 对 $D_{SKL}^{(\alpha )}(p^1,p^2)$ 的 $L_2$ 范数存在上界：
$$\begin{array}{rl}& \mathbb{E}[|D_{SKL}^{(\alpha )}(p_n^1,p_n^2)-D_{SKL}^{(\alpha )}(p^1,p^2){|}^2]\\ & \le \frac{c_1(\alpha )}{n^2}+\frac{c_2{\log }^2(\alpha n)}{n}+\frac{c_3{\log }^2(c_{4}n)}{{\alpha }^{2}n},\end{array}$$
其中，$\begin{array}{r}{c}_1(\alpha )=\min \left\{\frac{1}{{\alpha }^2},\frac{{\chi }^2(p^1,p^2{)}^2}{(1-\alpha {)}^2}\right\}\end{array}$，以及与 $n$、$\alpha$ 和 $D_{KL}(p_1,p_2)$ 无关的正常数 $c_2,c_3,c_4$，其中 ${\chi }^2(p^1,p^2)$ 表示 $p^1$ 与 $p^2$ 之间的卡方散度（chi-square divergence）。

温馨提示：
阅读全文请访问"AI深语解构" DISTILLM：迈向大型语言模型的简化蒸馏方法