pytorch入门2:利用pytorch进行概率预测
上一次中使用pytorch来进行了线性预测,线性预测输出的都是连续值,有时候我们并不需要使用输出具体的数值,我们只需要使用概率来判断一个时间是否发生,这时候我们就需要使用pytorch来进行概率预测,通过概率来实现对结果的判断;
(1)产生数据
假设这里有一些数据表明的是一个学生的平均每天的学习时间和最后期末考试是否通过的数据,我们可以使用这样的生成数据代码模拟这些数据
def creat_data(seed = 42, sample = 100):np.random.seed(seed)study_hour = 20 * np.random.random(sample).reshape(-1, 1)passed_hour = 6logits = (study_hour - passed_hour) * 0.5pro_pass = 1 / (1 + np.exp(-logits)) # 计算概率,其中以passed_hour为界作为50%的阈值passed = np.random.binomial(1, pro_pass) # 将概率作伯努利实验,模拟是否通过return study_hour, passed这段代码首先使用np.random.random生成100个0-1的数据,乘以20表示平均一天的学习时间,使用reshape为了后面便于转换为tensor,这里使用了一个函数将学习时间映射到0-1区间内,可以粗略地将这个当成是否通过考试的概率,随后使用np.random.binomial来将是否通过考试概率进行伯努利实验,最后返回学习时间和是否通过考试,通过为1,不通过为0;
(2)数据处理
将生成的数据转为pytorch运算数据tensor
study_hours_data, passed_data = creat_data()
study_hours = torch.tensor(study_hours_data, dtype=torch.float32)
passed = torch.tensor(passed_data, dtype=torch.float32)(3)构建模型
相对于线性模型,概率模型只有一点不同,那就是使用sigmoid将一个线性变换后的数据通过非线性变换映射到0-1之间,这个映射和构建数据时使用的函数一样
class sigmoid_model(nn.Module):def __init__(self):super(sigmoid_model, self).__init__()self.linear1 = nn.Linear(1, 1)self.sigmoid = nn.Sigmoid()def forward(self, x):x = self.sigmoid(self.linear1(x))return x
(4)进行训练
训练也和之前的线性模型基本一样,无非就是前馈,反馈和更新
update_times = 1000
total_loss = [0.0 for i in range(update_times)]
model = sigmoid_model()
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
for i in range(update_times):sigle_loss = 0.0passed_pre = model(study_hours)loss = criterion(passed_pre, passed)total_loss[i] = loss.item()if (i % 10 == 0):print(f"{i}: {loss.item()}")optimizer.zero_grad()loss.backward()optimizer.step()这里和线性模型唯一的不同就是损失函数的选择不同,通过前面的思维导图也可以看到,这里的损失函数选择的时二元交叉熵BCELoss
(5)模型预测
可以将训练好的模型进行预测,随便生成0-20的整数进行预测
model.eval()
with torch.no_grad():test_hour = torch.tensor([[i] for i in range(0, 20)], dtype=torch.float32)test_pre = model(test_hour)print(test_pre)fig, axs = plt.subplots(1, 2)
axs[0].plot(total_loss)
axs[1].plot(test_hour, test_pre)
axs[1].axvline(x=6, c='r', linestyle='--')
axs[1].axhline(y=0.5, c='r', linestyle='--')
axs[1].scatter(study_hours_data, passed_data)plt.show()最终损失函数和预测结果如下
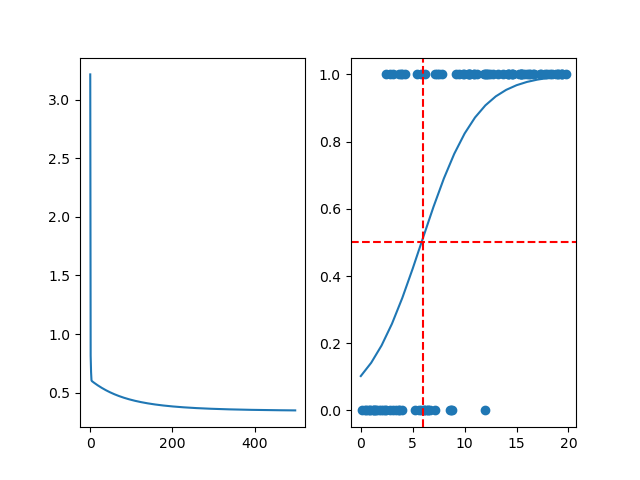
从最终结果中可以看出,模型预测的50%概率值在6附近,表示这个训练还是成功的,通过损失值也可以看出,最后损失值稳定;
如果我们减小一下优化器的学习率为0.01,输出如下:
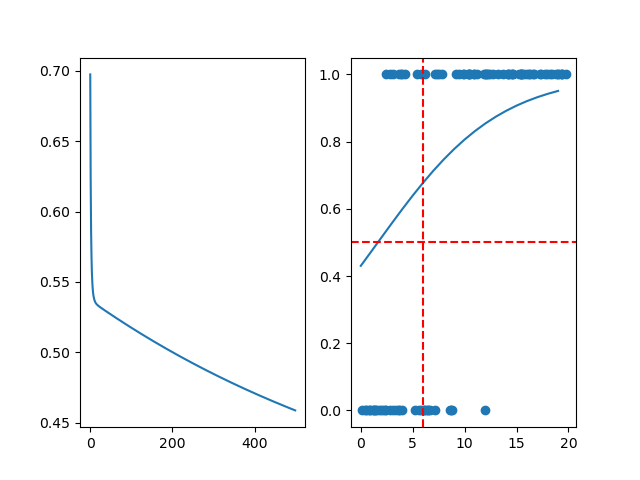
可以看到损失函数在最后并没有收敛,而且最后预测的结果和理想结果也有一些差异,这时候我们可以调高一下学习率或者增加学习次数以让训练收敛
